一种利用子结构综合技术的模型修正方法

王 陶， 何 欢,2， 闫 伟，陈国平,2

(1.机械结构力学及控制国家重点实验室, 南京 210016；2.南京航空航天大学 振动工程研究所, 南京 210016)

一种利用子结构综合技术的模型修正方法

王 陶1， 何 欢1,2， 闫 伟1，陈国平1,2

(1.机械结构力学及控制国家重点实验室, 南京 210016；2.南京航空航天大学 振动工程研究所, 南京 210016)

提出了基于改进自由界面子结构模态综合法的结构模型修正方法。首先给出了一种改进的自由界面子结构模态综合法，该方法通过构造一组与系统低阶模态加权正交的向量集，有效地解决了含有刚体模态时系统剩余柔度矩阵的求解问题。然后利用摄动法对每个子结构进行摄动，并计算灵敏度，通过子结构综合技术得到由摄动量表示的综合系统方程和灵敏度方程，给出了基于灵敏度分析的修正计算方法。该方法仅需对综合方程进行修正，极大的减缩了待修正问题的计算规模，提高了修正效率。最后，以典型数值算例验证了该方法的有效性。

自由界面；子结构模态综合；摄动法；模型修正

有限元模型修正技术是用来提高有限元模型预测准确性的有效方法。纵观模型修正技术近几十年的发展，主要可以分为矩阵型修正和参数型修正两大类，由于采用参数型修正后的修正量物理意义明确，修正后的模型与实际结构关联程度大，因此是当今主流的模型修正方法。

参数型模型修正问题通常被转化为优化问题进行处理[1-2]，通过在优化过程中不断迭代更新灵敏度矩阵和修正参数来完成修正过程。然而，随着当今工业技术的发展，机械结构日渐趋于大型化、复杂化，进而导致有限元模型的规模也越发庞大。采用传统方法进行修正，势必需要在灵敏度分析过程中付出高昂的计算代价。为此，在迭代修正这一环节中，部分学者借鉴在优化设计与可靠性分析中倍受重视的代理模型技术，使用代理模型来代替直接的有限元计算，实践证明该方法可有效的解决复杂模型的分析效率问题。郭勤涛等[3]利用结构动力学测试的响应结果构建了响应面模型，论证了基于响应面进行结构模型修正的可行性。SHYY等[4]对不同形式的响应面拟合精度和效率进行了研究，证实了双层径向基神经网络响应面具有较好的的拟合效果。YANG等[5]用Kriging响应面和多目标遗传算法对大展弦比飞机进行了模型修正，计算结果显示基于响应面的模型修正方法能在保证较高精度的基础上大幅提高计算效率。

然而基于代理模型的模型修正方法同样也存在其局限性。代理模型在构建过程中不可避免的会引入近似误差，而模型修正本身属于一类不适定性问题，微小的扰动可能造成修正结果与真实结果的偏离，因此代理模型的精度将直接决定修正效果。由于代理模型精度受制因素众多，建模过程对于研究人员的经验依赖较高，因此至今仍没有统一的高精度建模规范可供参考，极大的限制了该模型修正方法的推广。

基于以上原因，很多学者开始探寻其他高效的修正方法。近些年，部分研究人员将关注目光重新落在了子结构模态综合法[6-8]这类传统模型降阶方法上，通过将子结构模态综合法与模型修正问题相结合来提高大型复杂结构模型的修正效率。王毅等[9]将子结构模态综合法与模型修正方法结合对星箭模型进行了修正研究。张美艳[10]提出了一种新的求解特征灵敏度的结构动力重分析方法，并将求解特征值灵敏度的方法引入固定界面子结构模态综合法中，推导出了固定界面子结构综合模型特征参数的一阶和高阶灵敏度综合方程。侯吉林等[11]提出了一种以局部子结构为修正对象的约束子结构修正法。通过构造出的约束子结构柔度矩阵，运用迭代优化的方法修正约束子结构模型。WENG等[12]提出了一种子结构模型修正方法，对采用子结构模态综合得到的模型进行了灵敏度分析。PAPADIMITRIOU等[13]基于子结构模态综合法推导出了减缩修正方程，用减缩模型进行每个修正迭代步的计算，大大提高了模型修正问题的计算效率。JENSEN等[14]将固定界面法与贝叶斯模型修正方法相结合，通过一个框架结构对所提方法进行了验证。以上的研究多为通过固定界面模态综合法与模型修正相结合来提高模型修正的效率。然而在实际操作中，通常采用实验测得的数据对模型进行修正，而实验中固定界面的边界条件实现起来较为困难。于是开始有研究者尝试将自由界面模态综合法应用在模型修正问题中。文献[15-16]针对结构的动力学响应分析及常规的数值迭代算法运算效率较低的问题，提出了在自由界面模态综合法基础上的模型修正方法。

针对实验中固定界面不易实现的问题，本文在文献[17]的基础上提出了一种考虑剩余柔度的摄动自由界面子结构模态综合法。这种方法首先将结构分为若干子结构，采用摄动法对子结构进行摄动，然后根据子结构之间的界面协调条件推导出了含有模态参数摄动量的综合方程，通过减缩后的综合方程可直接求解出特征值关于修正变量的灵敏度。由于交界面采用了自由界面的连接方式，所以可以采用实验室中易于实现的自由边界条件的实验数据构造目标函数，将求解出的灵敏度进一步代入到优化算法中对机翼结构有限元模型进行了修正。因为本方法直接针对减缩模型进行修正，所以可以有效提高模型修正的效率。

1 子结构摄动方程

n自由度无阻尼离散振动系统的运动方程可以表示为：

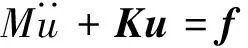
(1)

式中M和K∈Rn×n分别为系统质量矩阵和刚度矩阵，u和f∈Rn分别为广义位移向量和载荷向量。通过特征值分析可得到系统前l阶模态向量Φl∈Rn×l。

根据摄动法的思想，当结构修正变量参数发生小范围的变化后，结构系统的刚度、质量矩阵也会产生相应的改变，假设结构摄动后的刚度矩阵、质量矩阵表示为：

K=K0+ΔK

(2)

M=M0+ΔM

(3)

式(2)和式(3)中K0和M0是原系统的结构刚度矩阵和质量矩阵，ΔK和ΔM为是原系统结构刚度矩阵和质量矩阵的摄动量。同样，结构的模态向量也相应改变，即Φl=Φ0l+ΔΦl。

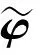
(4)

满足

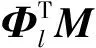
(5)

来构造一组与系统低阶模态加权正交的向量集。

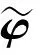
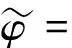
(6)

并将式(6)与考虑了摄动量的结构模态向量组代入式(4)和(5)得

φ=

化简可得

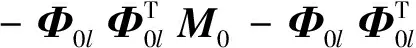
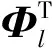
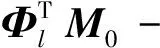
(8)

若只保留一阶微量，可得

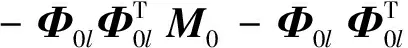
(9)

式中，Φ0l是原始结构系统前l阶模态向量，ΔΦl是结构设计参数改变后系统前l阶模态向量改变量。

u=Φβ

(10)

将结构模态向量代入到结构振动运动方程，可以将方程化简为：

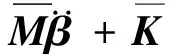
(11)

其中：

(12)

(13)

(14)

由于系统低阶模态向量和构造的加权正交向量关于质量矩阵正交，则易证明得到：

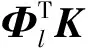
(15)

再结合式(5)可以将式(11)化简为：

(16)

令

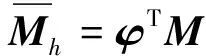
(17)

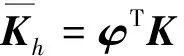
(18)

以上各式中的βl表示结构系统所要保留的低阶模态坐标，βh则表示结构系统需要被缩减的高阶模态坐标。

式(16)中的第二式可以表示为：

(19)

将式(19)经过Laplace变换后可以得到：

(20)

取式(20)中的一阶近似，然后再进行Laplace反变换后可以得到：

(21)

将式(21)代入式(10)中，化简可以得到：

u=(Φ0l+ΔΦl)βl+Gf

(22)

式中G∈Rn×n为剩余柔度矩阵，表达式如下式：

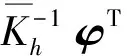
(23)

这里在求解剩余柔度矩阵G时，避免了直接对系统矩阵K求逆的过程，很好地解决了结构在自由-自由状态下系统矩阵K不可逆而无法计算剩余柔度矩阵的问题。

假设子结构的交界面上有m个自由度，且不考虑外力载荷的作用，将广义物理坐标按照内部坐标与界面坐标进行分块处理，写为如下形式：

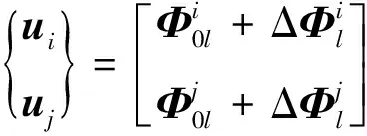
(24)

将式(24)中的第二式展开进行化简，可以将界面坐标表示为：

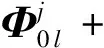
(25)

式中，Gjj∈Rm×m是结构剩余柔度矩阵与界面自由度uj对应的部分。

2 摄动方程的综合

假设这里以两个子结构a与b的连接为例，根据以上理论推导，由式(25)可以得到两个子结构的界面坐标表达式：

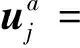
(26)

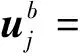
(27)

由子结构的位移连续性的协调条件和界面力平衡方程可以求解出界面力：

式中

(29)

综合式(16)以及式(28)，可得系统的综合方程为

(30)

式中

(31)

(32)

Mab=Mba=0

(33)

(34)

3 子结构综合模型灵敏度模型修正

3.1 子结构综合模型的灵敏度

求解子结构综合模型特征值灵敏度之前，必须先得到的刚度矩阵和质量矩阵对修正变量参数的导数，表达式如下：

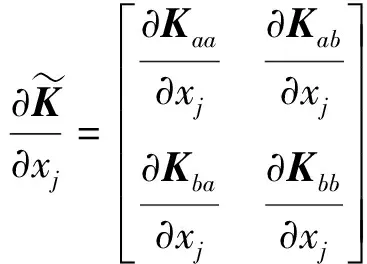
(35)

式中xj表示结构系统中第j个修正变量参数。

由式(34)可以计算子结构综合模型特征值的灵敏度：

(36)

当求解子结构综合模型的灵敏度时，每个子结构的修正变量参数是相互独立的，即结构的修正变量xj对整体系统的影响只与第j个子结构的刚度矩阵、质量矩阵有关，与其他子结构的结构参数无关。所以在求解灵敏度的时候，与修正变量参数xj没有关系的灵敏度都为零。只需计算与修正变量参数有关系的模态参数灵敏度。

3.2 子结构综合模型修正

模型修正可以转化为式(36)所表示的求解修正变量最优解的问题

(37)

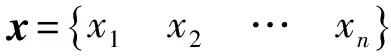
目标函数E(x)可以通过结构特征量建立的，体现了待修正模型仿真计算值与实验测量值之间的差异。

(38)

式中fai和fsi分别为待修正模型与实验模型的结构特征量，wi是各特征量的权系数，N是特征量数目。

通过灵敏度分析可以求解出目标函数的梯度向量，确定优化迭代的搜索方向，找到在搜索区间的最优步长。

采用优化迭代算法对目标函数进行寻优分析，根据收敛条件判断是否满足修正指标要求。

4 数值算例

4.1 某机翼有限元模型及子结构划分

如图1所示的某机翼结构有限元模型，图2所示为其的内部结构图。

为了验证本文所提出方法的有效性，本文中将整个机翼结构划分为两个子结构，其中子结构a(如图3所示)包含548个壳单元，501个节点，总计3 006个自由度；子结构b(如图4所示)包含450个单元，424个节点，总计2 544个自由度。其材料属性如表1所示。

表1 机翼结构有限元模型材料属性

图1 机翼整体结构模型Fig.1 Aircraft wing structure

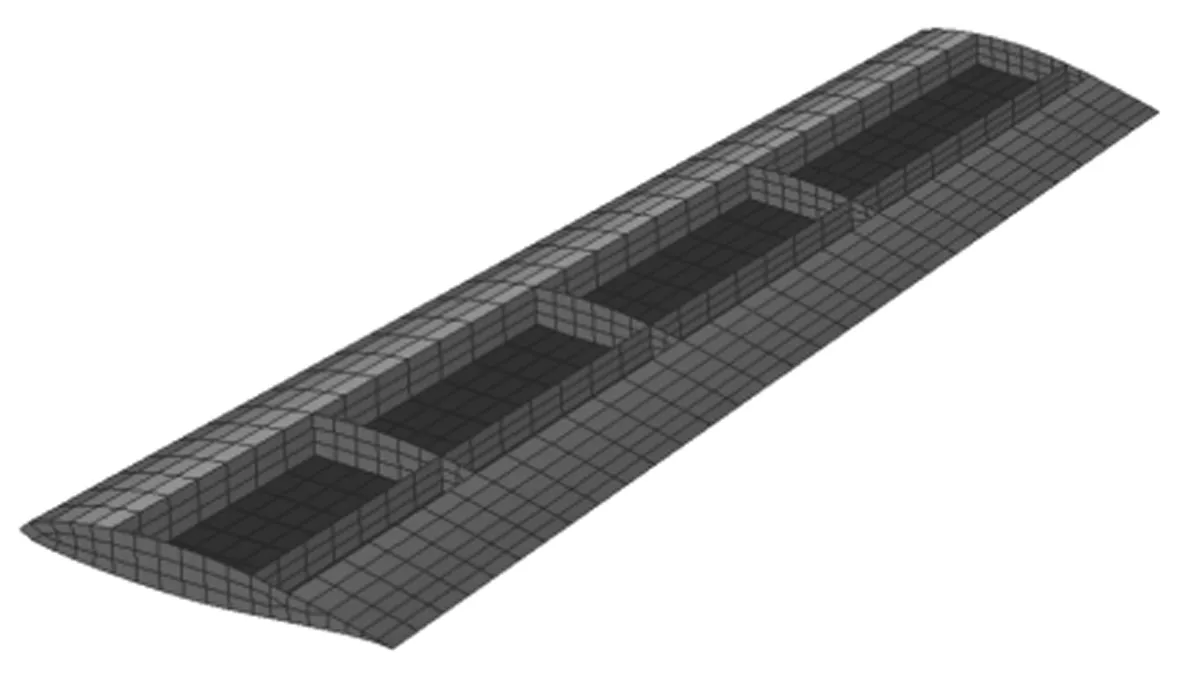
图2 机翼模型内部结构Fig.2 Internal wing structure

图3 机翼子结构a有限元模型Fig.3 Component a of wing structure

图4 机翼子结构b有限元模型Fig.4 Component b of wing structure

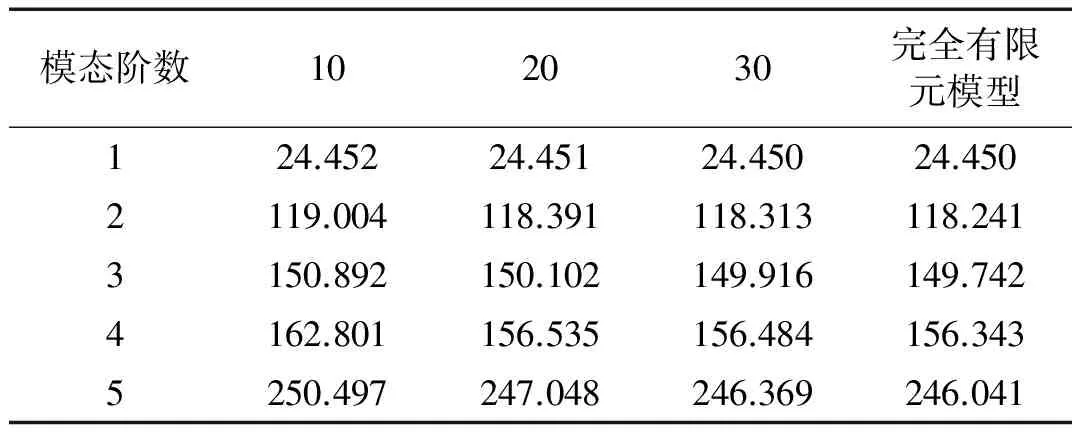
Tab.2 Comparison of the eigenvalues from the presented method and the full FEM Hz

首先采用子结构模态综合法，对机翼模型进行动特性分析，分别提取子结构前10、20和30阶低阶模态进行子结构综合，然后与完全有限元模型(FEM)的计算结果进行对比。

从表2可以看出，提取子结构前20阶低阶模态进行子结构综合已经可以达到较高的计算精度。为了使修正结果更加精确，后文采用提取子结构前30阶低阶模态的综合模型进行模型修正。

4.2 机翼有限元模型修正

这里采用梯度下降法对模型进行修正，其算法的整体流程如图5所示。

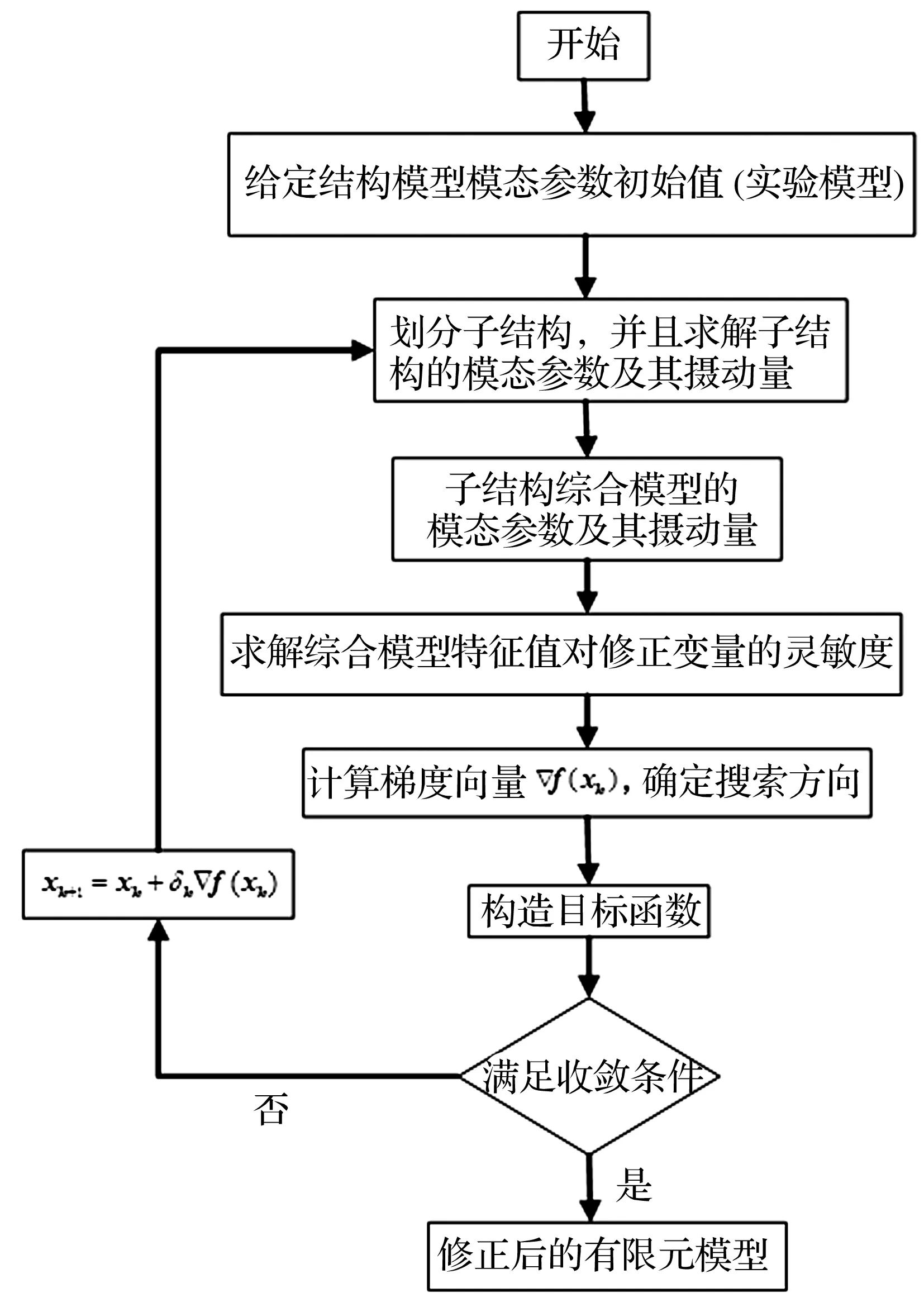
图5 模型修正算法流程图Fig 5.The flow chart of model updating

(1)构造目标函数

采用MSC.Patran/Nastran建模并将其计算的结果作为实验结果来对减缩后的模型进行模型修正，因此后文将MSC.Patran中建立的模型称为实验模型。

这里通过前五阶固有频率来构造优化分析的目标函数，记机翼试验模型的固有频率表示为ωs，机翼减缩模型计算得到的固有频率为ωa，则目标函数为：

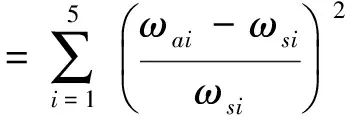
(39)

式中ωai是机翼有限元模型的第i阶固有频率，ωsi试验模型测试的第i阶固有频率。

(2)选择修正变量

结构修正变量在优化迭代的过程中随着迭代次数变化，结构的固有特性也会随着结构修正变量参数发生改变。

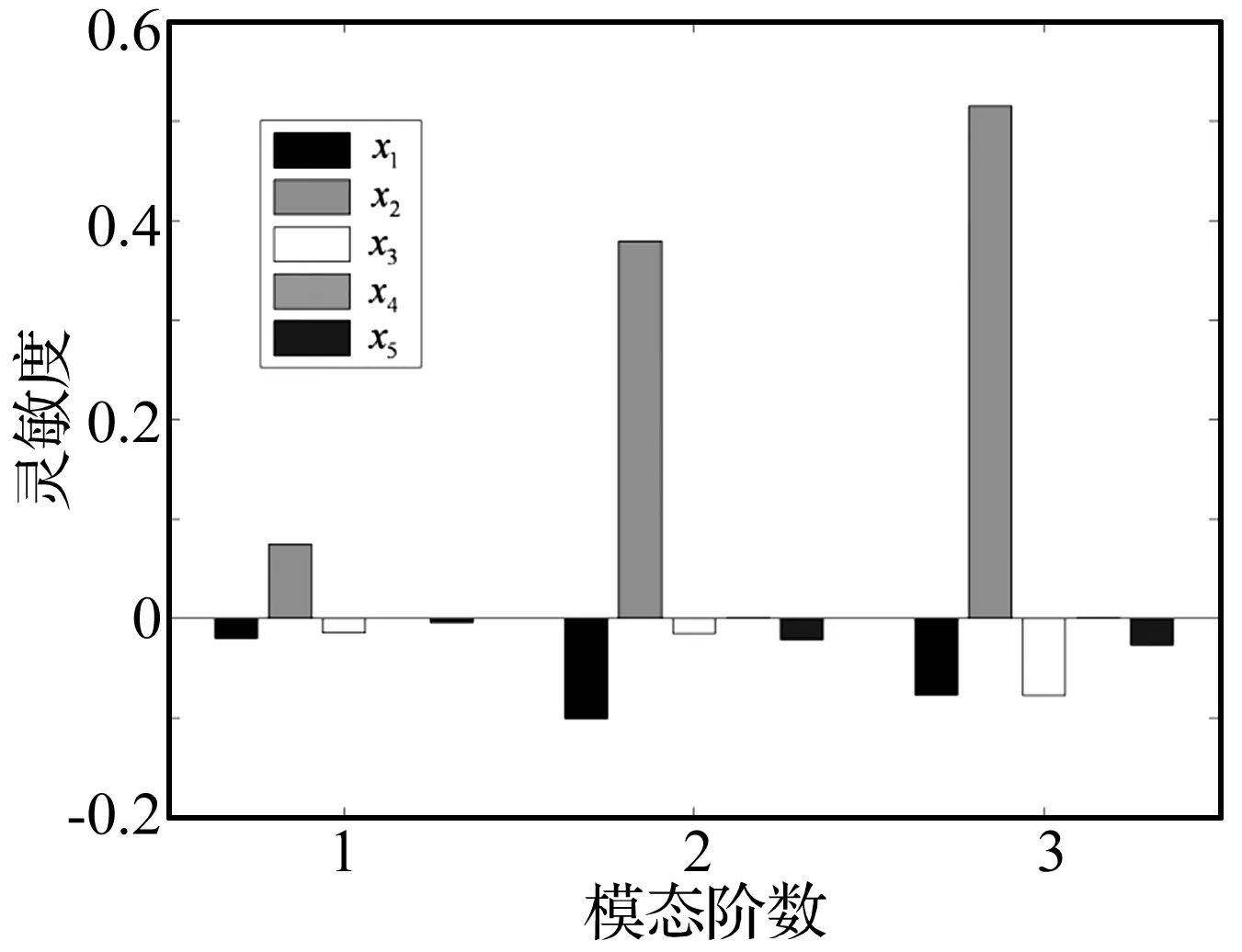
图6 各阶模态频率对修正变量的灵敏度Fig.6 Sensitivity of natural frequencies versus design variables

对于目标函数E(x)的变化，以各个修正变量的取值范围为约束条件，则其各个修正变量的变化范围为：

2.0 mm≤x1≤5.5 mm

1.5 mm≤x2≤3.0 mm

2.0 mm≤x3≤5.5 mm

(40)

(3)迭代收敛条件准则

目标函数的前后相对误差满足收敛容差：

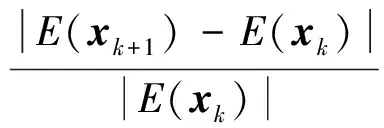
(41)

(4)机翼模型修正结果分析

图7给出了无量纲化处理的前五阶固有频率以及目标函数值随迭代次数的变化曲线。为便于对照，采用式(41)和(42)对频率以及目标函数值分别进行了归一化处理。

(42)

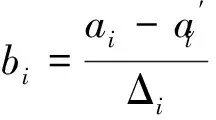
(43)

式中ai为要进行归一化的变量，其原本所处的区间为[a1ia2i]，bi为归一化后的变量，其所处的区间为[-1,1]。

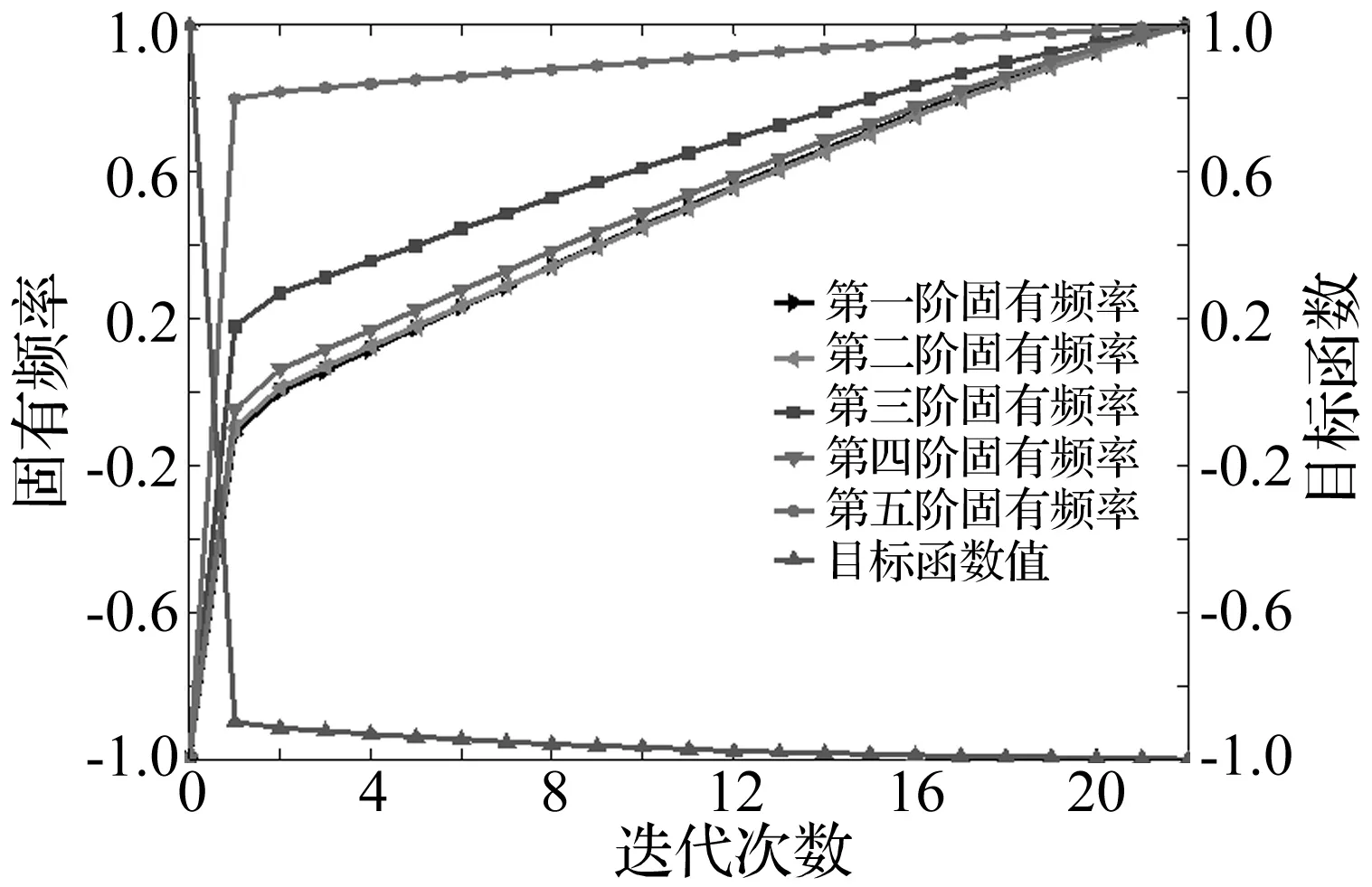
图7 固有频率与目标函数值的归一化迭代曲线Fig.7 Normalized natural frequencies and E(x)

从图7中可以看出，随着迭代次数的增加目标函数逐渐收敛，而各阶固有频率值逐渐趋向于修正值。

表3列举了所选修正变量在修正前后数值的对比，可以看出翼肋厚度的变化最为明显。从表4中所列举的数据可以看出，机翼结构模型修正后的固有频率与试验模型的前五阶固有频率误差很小，很好地说明了本文方法的有效性。

表3 机翼结构模型修正前后修正变量值对比

如图8所示，通过优化算法进行迭代计算，机翼结构模型的前五阶固有频率与实验模型间的误差都明显减小。另外，运用本文方法对机翼结构模型进行修正的计算时间约为直接对整体机翼结构进行修正时间的45%，说明采用本文的方法可以有效提高模型修正的计算效率。

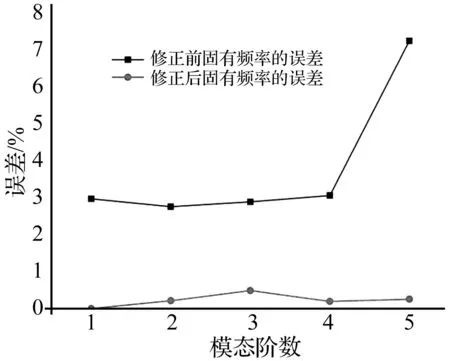
图8 机翼结构模型修正前后的固有频率误差对比Fig8. Errors of natural frequencies of wing before and after updating

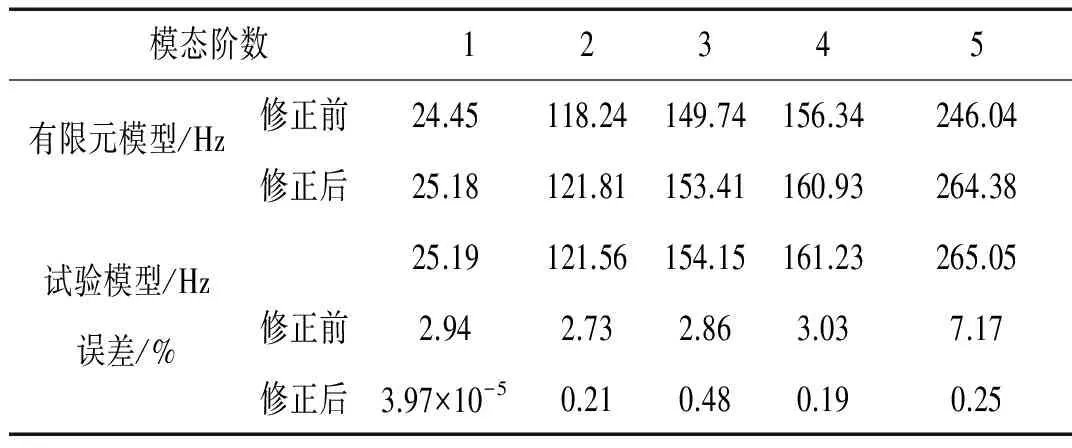
模态阶数12345有限元模型/Hz修正前24．45118．24149．74156．34246．04修正后25．18121．81153．41160．93264．38试验模型/Hz25．19121．56154．15161．23265．05误差/%修正前2．942．732．863．037．17修正后3．97×10-50．210．480．190．25

5 结 论

本文提出了一种基于改进自由界面子结构模态综合法的模型修正方法。该方法在进行模态综合的过程中通过构造一组与保留模态关于系统矩阵加权正交的向量集，使得在求解剩余柔度矩阵时避免了直接对刚度矩阵求逆，很好地解决了含有刚体模态时剩余柔度矩阵的求解问题。从而可以采用较为容易实现的自由边界条件的实验数据作为修正数据。

然后采用摄动法的思想推导了考虑摄动量的模态综合方程，并通过得到的综合方程构造了用于模型修正的灵敏度矩阵。采用减缩后模型所求得的特征值构造目标函数，并通过优化算法进行迭代求解以达到模型修正的目的。

最后通过数值算例对本文提出的方法进行了验证。从计算结果可以看出，采用本文提出的方法进行模型修正是有效的。并且由于采用了子结构模态综合法对模型进行了减缩，使得采用优化算法进行迭代计算时的效率有了较大提升。

[1] CHANG C, CHANG T Y P, ZHANG Q W. Iterative constrained optimization scheme for model updating of long-span bridges[J]. Proceedings of SPIE, 2000, 3995:334-345.

[2] TEUGHELS A,ROECK G D, SUYKENS J A K. Global optimization by coupled minimizers and its application to finite element model updating[J].Computer and Structures, 2003, 81:2337-2351.

[3] 郭勤涛，张令弥，费庆国.用于确定性计算仿真的响应面法及其试验设计研究[J]. 航空学报，2006,27(1):57-61. GUO Qintao, ZHANG Lingmi, FEI Qingguo. Response surface method and its experimental design for deterministic computer simulation[J]. Acta Aeronautica et Astronautica Sinica, 2006,27(1):57-61.

[4] SHYY W，TUCKER P K. Response surface and neural network techniques for rocket engine injector optimization[J]. Journal of Propulsion and Power，2001,17(2):391-411.

[5] YANG G W，CHEN D W. Response surface technique for static aeroelastic optimization on a high-aspect-ratio wing[J]. Journal of Aircraft，2009, 46(4):1444-1450.

[6] HURTY W C. Dynamic analysis of structural systems using component modes[J]. AIAA Journal, 1965, 3: 678-785.

[7] GOLDMAN R L. Vibration analysis by dynamic partitioning[J]. AIAA Journal, 1969, 7: 1152-1154.

[8] MACNEAL R H. A hybrid method of component mode synthesis[J]. Computers and Structures, 1971, 1(4): 581-601.

[9] 王毅,朱礼文,王明宇.大型运载火箭动力学关键技术及其进展综述[J].导弹与航天运载技术, 2000,243(1):1-9. WANG Yi, ZHU Liwen, WANG Mingyu. Summary of some key technologies on dynamics of large launch vehicle[J]. Missiles and Space Vehicles, 2000,243(1):1-9.

[10] 张美艳.复杂结构的动力重分析方法研究[D].上海:复旦大学,2007.

[11] 侯吉林,欧进萍.基于局部模态的约束子结构模型修正法[J].力学学报,2009,41(5):748-756. HOU Jilin, OU Jinping. Isolated substurcture model updating based on local mode[J]. Chinese Journal of Theoretical and Applied Mechanics, 2009,41(5):748-756.

[12] WENG Shun, XIA Yong, XU Youlin, et al. Substructure based approach to finite element model updating[J]. Computers and Structures, 2011, 89: 772-782.

[13] PAPADIMITRIOU C, PAPADIOTI D C. Component mode synthesis techniques for finite element model updating[J]. Computers and Structures, 2013, 126: 15-28.

[14] JENSEN H A, MILLAS E, KUSANOVIC D. The use of component mode synthesis techniques for large finite element model updating using dynamic response data[C]//Proceedings of the 9th International Conference on Structural Dynamics.Porto: EURODYN,2014: 2965-2971.

[15] 刘洋,段忠东,周道成.基于模态综合技术的结构有限元模型修正[J].振动、测试与诊断, 2009,29(3):287-291. LIU Yang, DUAN Zhongdong, ZHOU Daocheng. Finite element model updat ing of complex structure using component mode synthesis technique[J]. Journal of Vibration,Measurement&Diagnosis,2009,29(3): 287-291.

[16] LIU Yang, LI Yan, WANG Dejun, et al. Model updating of complex structures using the combination of component mode synthesis and Kriging predictor[J]. The Scientific World Journal, 2014(2014): 1-13.

[17] HE H, WANG T, CHEN G P, et al. A real decoupled method and free interface component mode synthesis methods for generally damped systems[J]. Journal of Sound and Vibration, 2013, 319: 335-354.

Model updating approach based on improved component mode synthesis

WANG Tao1, HE Huan1,2, YAN Wei1, CHEN Guoping1,2

(1.State Key Lab of Mechanics and Control for Mechanical Structures, Nanjing 210016, China;2. Institute of Vibration Engineering Research, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)

A model updating technique based on improved free-interface component mode synthesis was proposed. By constructing weighted-orthogonal vector sets which have weighted-orthogonal relationship with the lower retained modes, it is easier to obtain the residual flexibility attachment matrix. Each of the components was analyzed by perturbation method. Then the modal equation and the sensitivity equation of whole system were derived by using the component mode synthesis method. The model updating method based on sensitivity analysis proposed in the paper greatly reduces the model scale and improves the computational efficiency. The application of the proposed model updating method in a wing model calculation demonstrates that the presented method is effective.

free-interface; component mode synthesis; perturbation method; model updating

国家自然科学基金资助(11472132); 中央高校基本科研业务费资助(NS2014002); 机械结构力学及控制国家重点实验室(南京航空航天大学)自主研究课题资助(0113Y01); 江苏高校优势学科建设工程资助

2015-03-27 修改稿收到日期：2015-12-24

王陶 男，博士，1987年生

何欢 男，副教授，1978年生 E-mail:hehuan@nuaa.edu.cn

O321; TB123

A

10.13465/j.cnki.jvs.2017.02.024