基于EEMD和自相关函数峰态系数的轴承故障诊断方法

刘永强， 李翠省， 廖英英

(1.石家庄铁道大学 机械工程学院，石家庄 050043; 2.石家庄铁道大学 土木工程学院，石家庄 050043;3.河北省交通安全与控制重点实验室，石家庄 050043)

基于EEMD和自相关函数峰态系数的轴承故障诊断方法

刘永强1,3， 李翠省1， 廖英英2,3

(1.石家庄铁道大学 机械工程学院，石家庄 050043; 2.石家庄铁道大学 土木工程学院，石家庄 050043;3.河北省交通安全与控制重点实验室，石家庄 050043)

针对滚动轴承故障冲击信号周期性强且易被强烈的背景噪声所淹没的特点，提出了基于EEMD和自相关函数峰态系数的轴承故障诊断方法。首先，对采集到的复杂振动信号进行EEMD分解，根据自相关函数峰态系数和峭度准则重构IMF分量以突出故障特征信息；然后，利用谱峭度自动确定带通滤波器的最佳中心频率和带宽；最后，将滤波后的信号进行包络解调分析并与理论故障特征频率对比。通过轴承故障的仿真和实验研究，验证了该方法的有效性和可行性。

自相关函数；峰态系数；轴承；故障诊断

滚动轴承被广泛应用于各种旋转机械中，是较容易损坏的零件，其运行状态正常与否直接影响到整个机械系统的性能，因此滚动轴承的故障诊断具有重要的实际研究价值。

滚动轴承运行环境复杂，早期微弱故障信号往往被强噪声所湮没，不易被提取到。目前常用的研究方法主要集中于消噪和故障特征提取。小波消噪具有多分辨率等优点，但消噪效果很大程度上依赖于基函数和阈值的选择，缺乏自适应性[1-2]。经验模式分解(EMD)是一种自适应信号消噪方法，适合分析非线性、非平稳信号，但EMD分解存在着端点效应和模态混叠等现象。因此WU等[3]在EMD方法的基础上引入噪声辅助分析，提出了集成经验模态分解方法(EEMD)，可有效抑制模态混叠现象。共振解调法是最常用的轴承故障诊断方法，但需事先通过冲击试验确定带通滤波器的中心频率和带宽[4]，局限性比较大。王宏超等[5]利用Kurtogram算法自动确定带通滤波器最佳滤波中心和带宽，克服了人为确定带通滤波器参数的缺点。苏文胜等[6]依据相关系数和峭度准则选取IMF分量，彭畅等[7]采用度量因子筛选IMF分量，两者均结合谱峭度法滤波器功能，成功提取到了滚动轴承的故障特征频率。

本文针对轴承故障冲击信号周期性强，利用周期信号和随机信号自相关函数分布的差异性，提出了基于EEMD和自相关函数峰态系数的轴承故障诊断方法。依据自相关函数峰态系数和峭度准则筛选IMF分量，对重构信号进行基于谱峭度法的共振解调分析，有效地提取出故障信息特征。

1 基于自相关函数峰态系数的EEMD方法

1.1 EEMD原理及理论

集成经验模态分解方法是一种噪声辅助信号处理方法，通过多次给原信号中加入给定幅值的白噪声，利用白噪声频谱的均匀分布统计特性，使不同频带尺度的信号自动映射到合适的参考尺度上，克服了极值点上下包络线的拟合误差，从而有效地避免模态混叠现象。对多次分解的IMF叠加求平均，以达到消除噪声影响的目的。

EEMD的具体算法归结如下：

(1)对分析信号x(t)加入白噪声序列，并对加噪后的信号进行归一化处理。

(2)将包含白噪声的信号进行EMD分解，得到k个IMF分量cj(t)和一个余量r(t)，(j=1,…,k)。

(3)每次加入不同的白噪声序列，重复步骤(1)、(2)N次，即

(1)

式中：xi(t)为第i次加入白噪声后的信号；cij为第i次加入白噪声后分解得到的第j个IMF，j=1,…,k。

(4)求每次分解得到对应IMF的总体平均，消除多次加入高斯白噪声对真实IMF的影响，最终得到EEMD分解后的IMF为：

(2)

式中：N为EMD的集成次数；ci.j(t)为第i次EMD所得到的第j个IMF。

1.2 峭度和谱峭度(SK)

峭度是反映振动信号分布尖峰程度的数值统计量，对于冲击类故障信号的反应比较准确。正常轴承的振动信号近似服从正态分布, 其峭度值约为3, 而轴承出现故障时, 其峭度值明显增大。峭度值越大，故障冲击成分越明显。

(3)

式中：μ和σ分别是振动信号x(t)的均值和标准差，E表示取数学期望。

谱峭度(SK)最早由DWYER[8]提出，其基本原理是计算每根谱线的峭度值，从而提取出发生冲击的频带。ANTONI等[9-10]对谱峭度进行了深入的研究,给出了谱峭度的数学定义，并将其成功应用到旋转机械的故障诊断中。考虑非平稳信号的Wold-Cramer分解, 定义Y(t)为由信号x(t)激励的系统响应, 则Y(t)可以表示为：

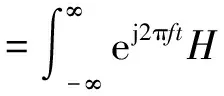
(4)

式中：H(t,f)是系统的时变传递函数,表示Y(t)在频率f处的复包络。

基于四阶谱累积量的谱峭度定义为：

(5)

式中：S2nY(f)为2n阶瞬时矩,用来度量复包络能量,定义为：

(6)

谱峭度可定义为：

(7)

滚动轴承的振动信号可用如下模型表示：

x(t)=z(t)+n(t)

(8)

式中：x(t)为实测振动信号，z(t)为纯净故障信号，n(t)为噪声信号。分别用Kx(f)和Kz(f)表示实测振动信号和纯净故障信号的谱峭度，则有：

(9)

式中：ρ(f)为噪声与实际振动信号的功率谱密度之比。由式(9)可知，在信噪比很大的频率处，Kx(f)和Kz(f)近似相等，噪声很强的频率处，Kx(f)近似等于零。

1.3 自相关函数及峰态系数

随机信号的自相关函数反映了信号与其本身在不同时刻的相似程度，是一种时间域的统计度量方法，定义为[11]：

Rx(t1,t2)=E[x(t1)x(t2)]

(10)

式中：x(t)为随机信号，其归一化自相关函数为：

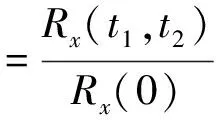
(11)

式中：Rx(0)表示信号与其本身在同一时刻的相关函数值，可知任何随机信号这一值都为最大值。

白噪声自相关函数的特点是只与自身相关，其他情况几乎为零，这与一般周期信号的自相关函数不同，结果如图1所示。从图上可知，随机噪声的自相关函数在零点处最大，向两侧迅速衰减为零；虽然一般周期信号在零点处同样取得最大值，但向两侧衰减为零的过程是缓慢的。

为了能定量地描述出相关函数的分布特点，本文引入峰态系数作为度量指标。在正态分布情况下，峰态系数值是零。正的峰态系数表明观察量更集中，有比正态分布更长的尾部；负的峰态系数表明观测量不那么集中，有比正态分布更短的尾部，类似于矩形的均匀分布。峰态系数越大，说明数据分布曲线越陡峭。

(12)

式中：N为信号x(t)的点数，σ为信号x(t)的标准方差。

计算图1(b)、(d)和(f)的峰态系数，分别为0.85、650.4和2.56。可知，随机信号的自相关函数分布曲线比较陡峭；带噪声的周期信号其自相关函数分布较单纯的周期信号要陡峭。

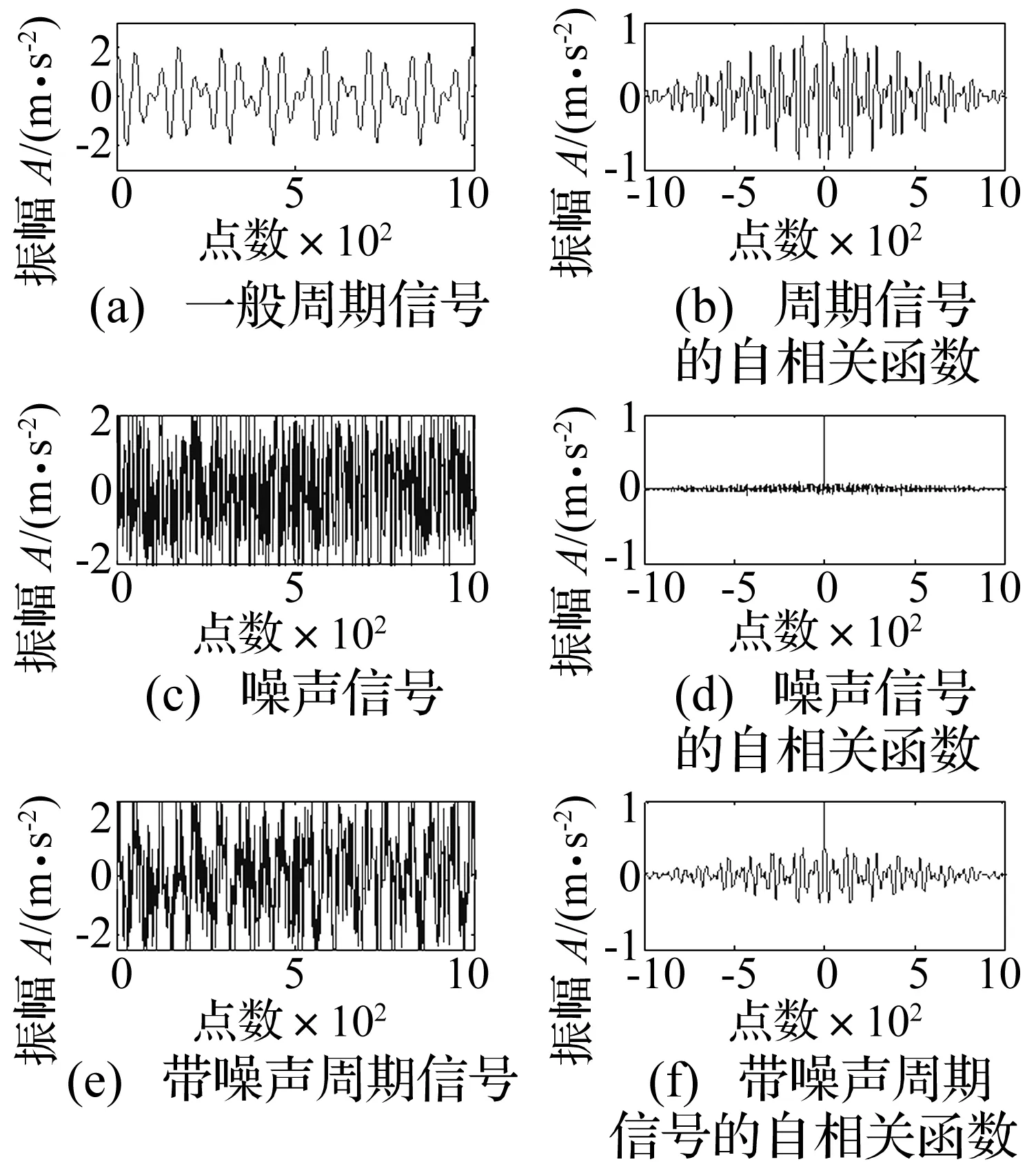
图1 周期信号和噪声信号及自相关波形Fig.1 Periodic signal and noise signal and autocorrelation waveform

1.4 轴承故障诊断流程

EEMD能自适应地将信号从高频到低频逐次分解出具有不同振动模式的IMF分量，高频部分的IMF分量中包含较多的故障冲击成分，然而其中往往含有大量的噪声，所以IMF分量的选取为EEMD分解的关键。本文采用峭度和相关函数峰态系数作为筛选IMF分量的准则。峭度值大于3即可判定信号中含有故障信息，本文经过多次试验，得出峰态系数的阈值设定为原故障信号自相关函数峰态系数的10倍比较合适，大于阈值即为强噪声。首先计算各个IMF的峭度值及其自相关函数的峰态系数，选取峭度值大于3且峰态系数小于阈值的IMF分量进行重构，这样既能保留最多的故障信息又能避免强噪声的干扰。然后将重构信号进行基于谱峭度法的共振解调分析，从而精确有效地提取到故障特征信息。其具体流程如图2所示。

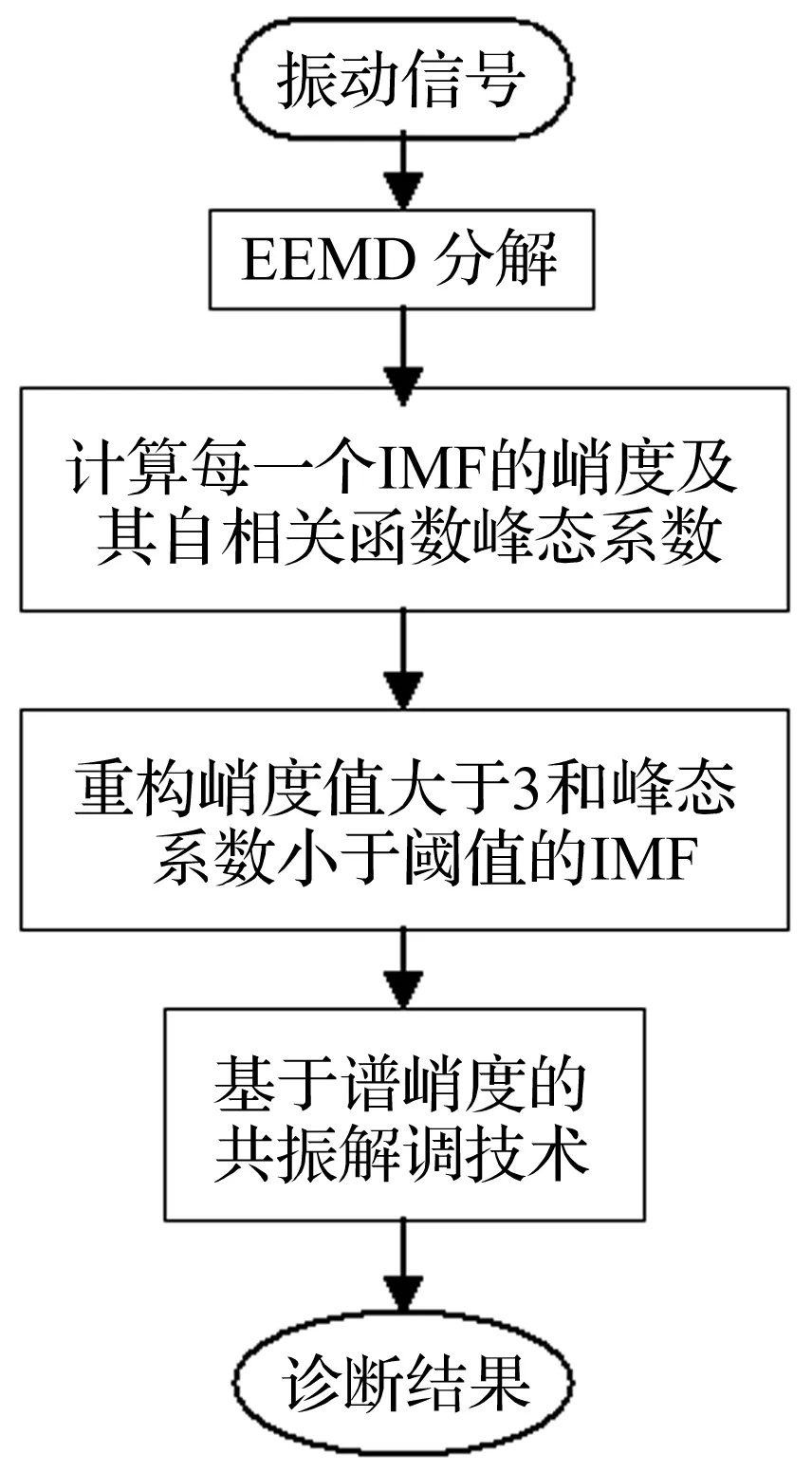
图2 轴承故障特征提取流程图Fig.2 The flow chart of the rolling bearing faults diagnosis

2 仿真信号分析

为了验证本文方法的正确性和有效性，首先利用滚动轴承故障时的仿真信号进行研究分析。

2.1 信号仿真

仿真信号由冲击信号、噪声信号和谐波信号3部分组成，以此来模拟滚动轴承发生早期故障时的单点损伤振动模型，其表达式为:

(13)

式中:α为衰减率，A为冲击幅值,t为时间，f1为冲击导致的共振频率；B为噪声幅值,z为随机数；C为谐波幅值，f2为谐波频率(转频)。

2.2 验证与分析

设冲击导致的共振频率f1为3 kHz,采样频率fs为25.6 kHz，转频f2为10 Hz，冲击信号的频率(故障频率)fm为180 Hz，信号时长1 s。仿真信号的时域图和频谱图分别如图3(a)、(b)所示。由于噪声的严重干扰，从图3(a)上难以看到故障冲击成分，图3(b)上也只能看到转频，发现不了故障频率。

将故障仿真信号进行EEMD分解，得到12个IMF分量，前3个IMF分量的时域波形如图4所示。计算各个IMF分量的峭度值及其自相关函数的峰态系数，如表1所示。原信号的自相关函数峰态系数为89.98。由表1知IMF1的峭度值为2.13，峰态系数为7 033，可知其完全为噪声。IMF2、IMF3和IMF7的峭度值大于3且峰态系数小于阈值，对其进行重构,时域波形如图5(a)所示，可以看到明显的冲击成分。图5(b)为重构信号帯通滤波后的包络谱，可以清楚地看到故障频率及其倍频。仿真分析结果验证了本文方法的正确性和有效性。

图3 滚动轴承仿真信号Fig.3 The simulation signal

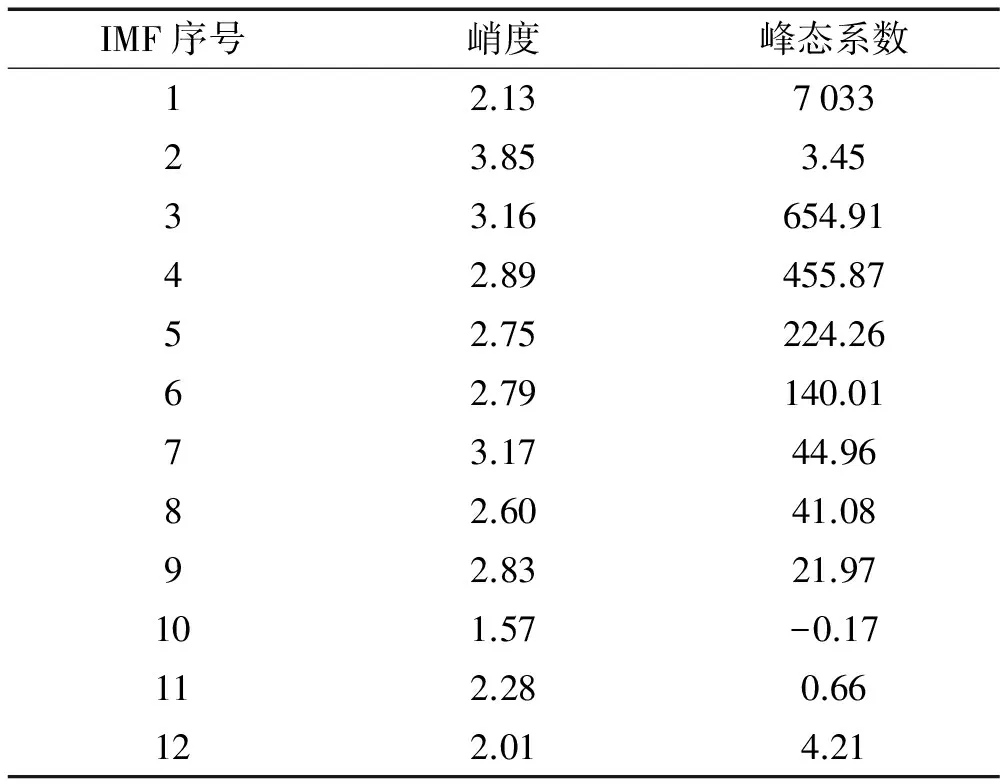
IMF序号峭度峰态系数12．13703323．853．4533．16654．9142．89455．8752．75224．2662．79140．0173．1744．9682．6041．0892．8321．97101．57-0．17112．280．66122．014．21

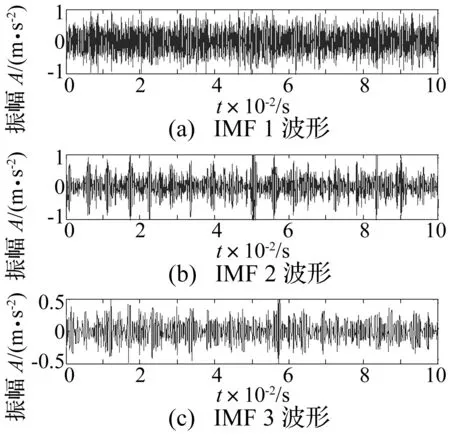
图4 前3个IMF分量Fig.4 The previous three IMFs

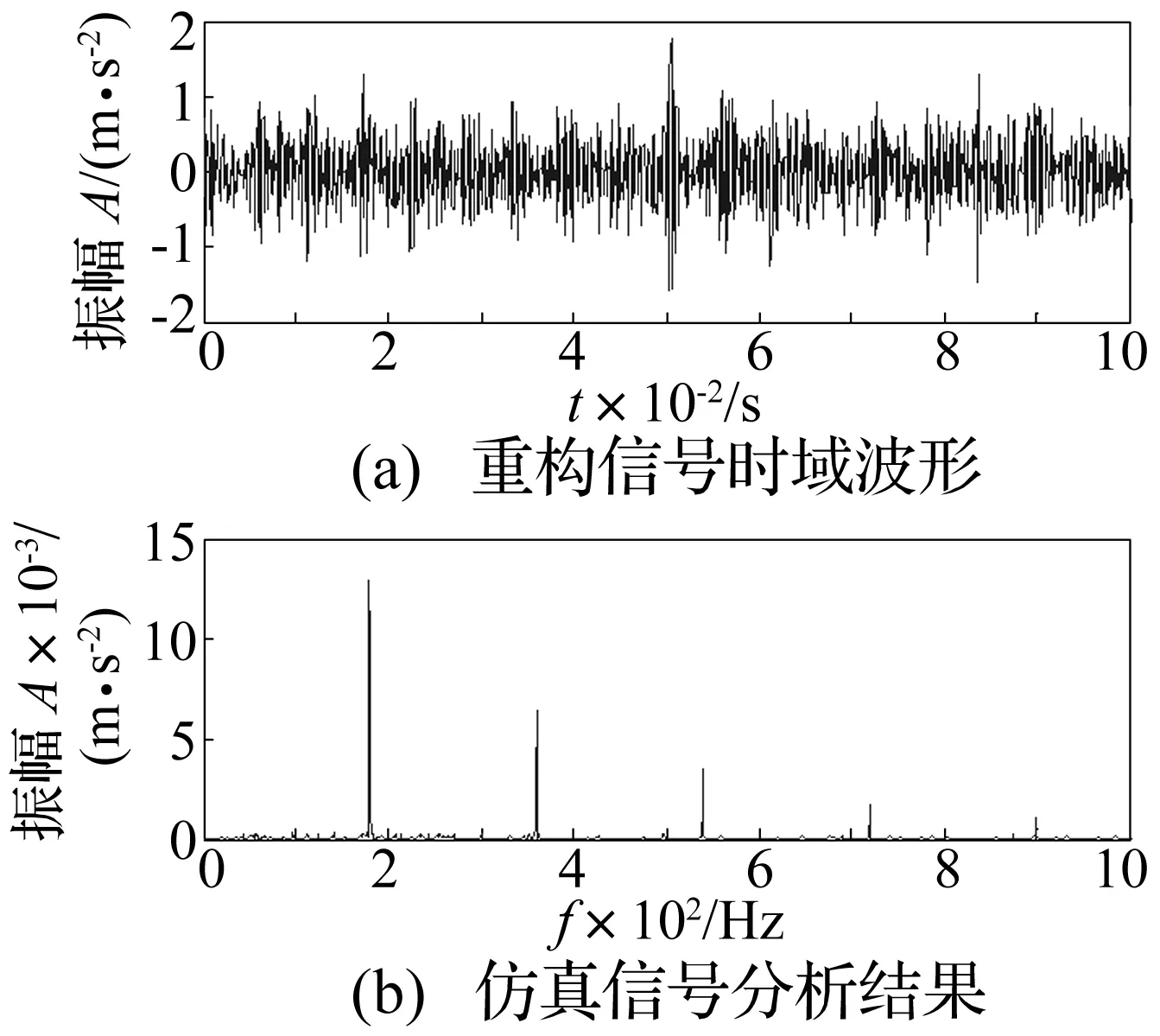
图5 重构信号Fig.5 The reconstruction signal

3 实验研究

3.1 实验装置

为了验证该方法的有效性和可行性，将其应用于铁路货车滚动轴承的故障诊断中。铁路货车运行环境复杂，背景噪声强，轴承故障特征信息难于提取。在轮对滚动轴承故障诊断实验台上一侧安装正常状态轴承，另外一侧安装故障轴承，实验台及传感器安装位置如图6和图7所示。实验台采用的是 RD2型轮对和与之相匹配的197726 型双列圆锥型滚动轴承，其主要参数如表2所示。实验装置包括CA-YD-188型压电式加速度传感器、信号放大器、INV36DF型信号采集仪、DASP数据处理软件等。

表2 197726 型轴承主要参数

图6 轮对跑合试验台Fig．6Wheelsetrunningtesting图7 传感器安装位置Fig．7Sensorsinstallationlocation

3.2 实验数据及分析

选取轮对速度为465 r/min，采样频率为12 800 Hz时的内圈故障数据进行EEMD分解，得到15个IMF分量和1个余量，前3阶IMF 分量的时域波形如图8所示。计算各IMF的峭度值及其自相关函数峰态系数，如表3所示。原信号的自相关函数峰态系数为152.14。由表3知IMF1的峭度值为4.59，而峰态系数为5 227.7大于阈值，为避免强噪声的干扰剔除IMF1。将分量IMF2、IMF3、IMF4、IMF5和 IMF12进行重构,时域波形如图9(a)所示，可以看到明显的冲击成分。文献[12]将峭度值大于3的所有IMF进行重构，其时域波形如图9(b)所示；图9(a)较图9(b)可以看到更加明显的冲击成分，证明了该方法的优越性。

图8 前3个IMF分量Fig.8 The previous three IMFs

IMF序号峭度峰态系数14．595227．727．08348．835．13407．544．32104．353．462．9662．935．5672．520．2282．850．6192．370．11102．6928．17112．6613．08123．719．65132．200．81142．841．43151．50-0．26

图10为重构信号帯通滤波后的包络谱图，可以看到故障特征频率88.18 Hz(接近内圈的理论故障特征频率88.03 Hz)及其倍频176.4 Hz、264.6 Hz,基频和二倍频谱线都很突出，三倍频谱线虽不突出，但也可辨别。包络谱中同时可看到转频7.8 Hz(接近转频理论值7.75 Hz)及其倍频15.5 Hz、23.3 Hz，间距为转频的调制边带。由此典型特征可以诊断为内圈故障。图11为基于谱峭度法的共振解调分析的包络谱图，没有经过EEMD降噪处理，故障特征频率谱线不突出，并且没有故障频率和转频的3阶频谱线。比较图10和图11，可以看出本文方法的精确性。

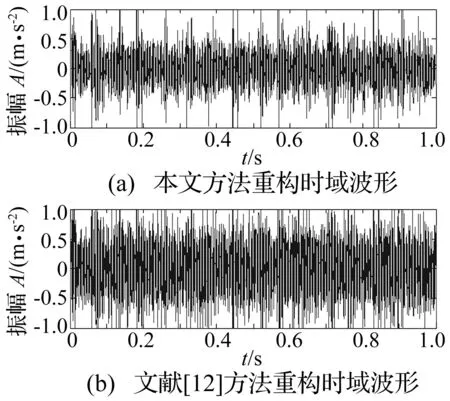
图9 本文及文献[12]时域波形Fig.9 The time domain waveform of this paper and the reference[12]

图10 实测信号的包络谱Fig.10 Envelope spectrum of measured signal

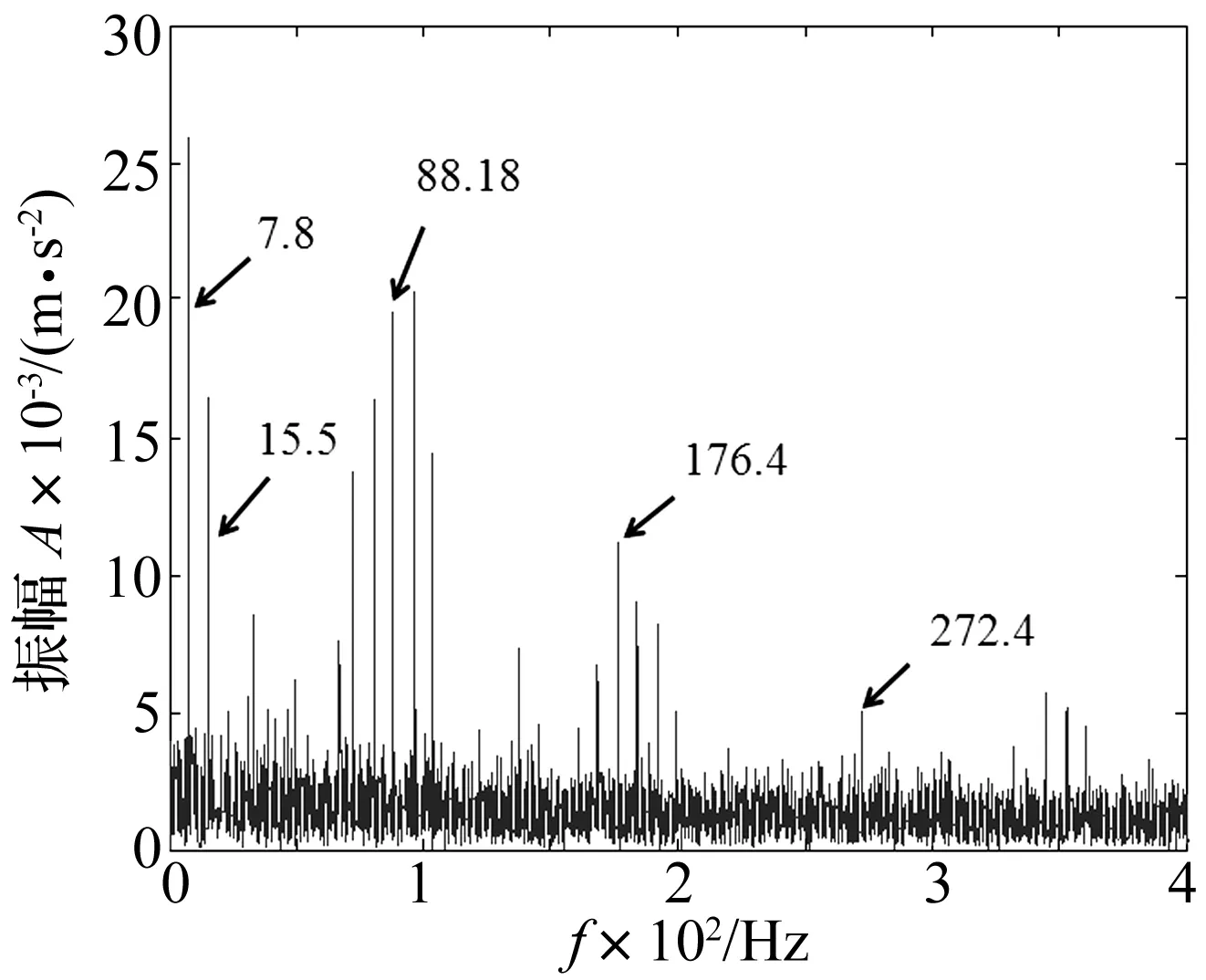
图11 无EEMD降噪处理的实测信号包络谱Fig.11 Envelope spectrum of measured signal without EEMD

4 结 论

本文针对滚动轴承早期故障提取困难的特点，提出了基于EEMD和自相关函数峰态系数的轴承故障诊断方法。采用EEMD方法对信号进行降噪处理，依据峭度和自相关函数峰态系数筛选IMF分量，达到了降低噪声突出故障特征信息的目的。利用谱峭度自动、准确地确定带通滤波器参数。EEMD降噪与谱峭度的结合，可以有效地抑制噪声，提高故障诊断的精确度。通过故障仿真信号和工程实测信号的研究分析，验证了本文所提方法的有效性和可行性。

[1] DONOHO D L, JOHNSTONE I M. Ideal spatial adaptation by wavelet shrinkag [J]. Biometrika Trust, 1994, 81(3): 425-455.

[2] 郭代飞, 高振明, 张坚强. 利用小波门限法进信号去噪[J]. 山东大学学报, 200l, 36 (3): 306-311. GUO Daifei, GAO Zhenming, ZHANG Jianqiang. Application of wavelet threshold to signal de-noising[J]. Journal of Shandong University,200l, 36 (3): 306-311.

[3] WU Z H, HUANG N E. Ensemble empirical mode decomposition: a noise assisted data analysis method [J]. Advances in Adaptive Data Analysis, 2009, 1 (1): 1-41.

[4] 王平, 廖明夫. 滚动轴承故障诊断的自适应共振解调技术 [J]. 航空动力学报,2005,20(4):606-612. WANG Ping, LIAO Mingfu. Adaptive demodulated resonance technique for the rolling bearing fault diagnosis [J]. Journal of Aerospace Power, 2005, 20 (4):606-612.

[5] 王宏超,陈进,董广明,等.基于快速kurtogram算法的共振解调方法在滚动轴承故障特征提取中的应用[J]. 振动与冲击, 2013, 32 (1): 35-37. WANG Hongchao, CHEN Jin, DONG Guangming, et al. Application of resonance demodulation in rolling fault feature extraction based on fast computation of kurtogram[J]. Journal of Vibration and Shock,2013, 32 (1): 35-37.

[6] 苏文胜, 王奉涛, 张志新，等. EMD 降噪和谱峭度法在滚动轴承早期故障诊断中的应用[J]. 振动与冲击, 2010, 29 (3): 18-21. SU Wensheng, WANG Fengtao, ZHANG Zhixin, et al. Application of EMD denoising and spectral kurtosis in early fault diagnosis of element bearings [J]. Journal of Vibration and Shock, 2010, 29 (3):18-21.

[7] 彭畅, 柏林, 谢小亮，等. 基于EEMD、度量因子和快速峭度图的滚动轴承故障诊断方法[J]. 振动与冲击, 2012, 31(20): 143-146. PENG Chang, BO Lin, XIE Xiaoliang, et al. Fault diagnosis method of rolling element bearings based on EEMD, measure-factor and fast kurtogram [J]. Journal of Vibration and Shock, 2012, 31(20): 143-146.

[8] DWYER R F. Detection of non-gaussian signals by frequency domain kurtosis estimation [C]//Acoustic, Speech and Signals Processing. Boston: IEEE Inter-national Conference on ICASSP,1983:607-610.

[9] ANTONI J,RANDALL R B. The spectral kurtosis: a useful tool for characterizing non-stationary [J]. Mechanical Systems and Signal Processing, 2006, 20(2): 282-307.

[10] ANTONI J, RANDALL R B. The spectral kurtosis: application to the vibratory surveillance and diagnostics of rotating machines [J].Mechanical Systems and Signal Processing, 2006, 20(2): 308-331.

[11] 余发军, 周凤星. 基于EEMD 和自相关函数特性的自适应降噪方法[J]. 计算机应用研究，2015, 32(1): 206-209. YU Fajun, ZHOU Fengxing. Adaptive de-noising method based on EEMD and autocorrelation function property[J].Journal of Application Research of Computers,2015, 32(1): 206-209.

[12] 王旭, 彭畅,张振先. 基于EEMD的共振解调技术在列车轴承故障诊断中的应用[J]. 现代电子技术，2015, 38(21): 24-27. WANG Xu, PENG Chang, ZHANG Zhenxian. Application of EEMD-based resonance demodulation technology in train bearing fault diagnosis[J]. Journal of Modern Electronics Technique, 2015, 38(21): 24-27.

Fault diagnosis method for rolling bearings based on EEMD andautocorrelation function kurtosis

LIU Yongqiang1，3, LI Cuixing1, LIAO Yingying2，3

(1.School of Mechanical Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China；2.School of Civil Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China；3.Key Laboratory of Traffic Safety and Control in Heibei, Shijiazhuang 050043, China)

Considering that fault shock signals of rolling bearings have the features of periodicity and easily immerging in background noise, a fault diagnosis method based on the EEMD and autocorrelation function kurtosis was proposed. Bearing fault signal was decomposed by EEMD method, and according to the autocorrelation function kurtosis and the kurtosis criterion, the IMF components, which contain much more fault information, were chosen to reconstruct a new composite signal. By virtue of the spectral kurtosis analysis of the new composite signal, a band-pass filter was designed. The new composite signal was filtered by the band-pass filter, further envelope demodulated and then compared with the theoretical failure frequency. A case study on bearing faults simulations and experiments verifies the effectiveness and feasibility of the method proposed.

autocorrelation function; coefficient of kurtosis; bearing; fault diagnosis

国家自然科学基金(11227201;11472179;U1534204;11572206;11302137;11172182;11372199);河北省自然科学基金(A2015210005);河北省教育厅项目(YQ2014028);河北省人才工程培养经费资助科研项目(A2016002036)

2016-02-23 修改稿收到日期：2016-05-08

刘永强 男，博士，副教授，1983年生

TH133.33

A

10.13465/j.cnki.jvs.2017.02.018