EMD和FSWT组合方法在爆破振动信号分析中的应用研究

杨仁树， 付晓强， 杨国梁， 陈 骏， 陈 玮

(中国矿业大学(北京)，力学与建筑工程学院，北京 100083)

EMD和FSWT组合方法在爆破振动信号分析中的应用研究

杨仁树， 付晓强， 杨国梁， 陈 骏， 陈 玮

(中国矿业大学(北京)，力学与建筑工程学院，北京 100083)

针对传统经验模态分解EMD时频分析功能不足的缺陷，提出了基于经验模态分解EMD和频率切片小波变换FSWT组合的爆破振动信号分析方法。对实际工程采集到的爆破振动信号进行EMD分解，根据相关性系数确定优势分量实现信号重构，并获取重构信号全频带FSWT时频特征。利用FSWT逆变换能切割任意频率区间的特点，将重构信号选择时间、频率切片区间进行了更为细化时频特征提取。研究了EMD-FSWT组合方法、Hilbert-Huang变换(HHT)、小波变换(WT)三种方法的消噪滤波效果，并与短时Fourier变换(STFT)、重排平滑Wigner-Ville分布(RSPWVD)两种传统时频方法进行了对比。分析结果表明：EMD-FSWT组合方法，对瞬态信号在时频域上的分辨率更高，消噪和滤波效果好，适于对爆破振动信号进行更为精细化的时频特征分析。

爆破振动；经验模态分解；频率切片小波；时频分析；能量分布

爆破振动信号具有典型的非平稳特性，单纯采用时域或频域分析方法很难精确提取其所包含的有效特征信息。因此，时频分析方法，如短时傅里叶变换(Short Time Fourier Transform,STFT)、小波变换(Wavelet Transform,WT)、魏格纳分布(Wigner-Ville Distribution，WVD)等，都越来越广泛地应用于爆破振动信号分析领域，取得了显著的成效。但这些方法在应用上都存在一定的局限性[1]。

1998年HUANG N E提出的HHT算法，它不受傅里叶分析的局限，具有多分辨率和自适应的特点，是一种更有效的时频局部化分析方法，适用于非线性非平稳信号的分析。但算法中EMD分解在低频段易产生一些不相关的IMF，不能分离低能量信号成分等缺陷使其频谱分析功能不足[2]。

严中红等[3]提出了频率切片小波变换(Frequency Slice Wavelet Transform，FSWT)理论并将其用于瞬态振动信号分析，该算法克服了传统EMD分解时频理论中严格的可容许性限制,可灵活实现信号的滤波和分割。郭涛等[4]成功将该算法引入到了爆破振动信号时频特征分析中，收到了良好的效果。本文在阐述EMD分解和频率切片小波变换理论基础上,提出了基于EMD和FSWT组合方法，融合了两种分析方法的优点并将其应用于爆破振动信号频谱分析中，揭示了爆破振动信号所包含的内在细化特征。

1 组合算法基本原理

1.1 EMD分解[5]

HHT变换中的EMD算法是依据分析信号本身的局部特征进行自适应分解，得到一系列具有不同特征时间尺度的IMF(Intrinsic Mode Function)分量。采用EMD方法对给定信号f(t)进行分解,最终原始信号f(t)可分解为若干IMF分量和一个余项rn(t)的和，即：

(1)

信号f(t)经EMD分解得到的各分量是具备完整性和正交性的，并且分解是自适应的，使信号分解更加灵活。但仍然存在一些不足，如不能分离低能量信号成分，容易引起模态混叠以及交叉项的干扰等，致使后续信号时频分析功能不足，仍需不断改进和完善。

1.2 FSWT算法[6]

令L2(R)为有限向量空间(R为实数集合)，对于任意信号f(t)∈L2(R),频率切片小波变换以母小波函数p(t)的傅里叶变换存在为前提，即：

W(t,ω,λ,σ)=

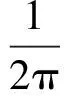
(2)

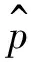
W(t,w,λ,σ)=

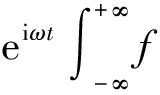
(3)

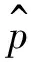
1.3FSWT尺度因子选取[7]

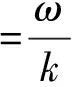
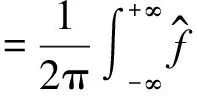
(4)

式中，k与ω、u无关，用其调节变换对频率或时间的灵敏度，称为时频分辨系数。

为获得均衡的时间和频率分辨率，对分析信号引入2个评价参数η、v，其中η称为频率分辨比率：

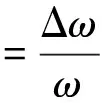
(5)

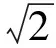
(1)若f(t)=eiω0t，且其FSWT满足：

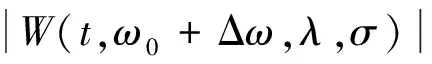
(6)

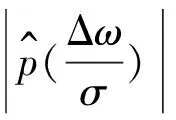
(2)若脉冲函数f(t)=σ(t-t0)，且其FSWT满足：

(7)

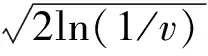
(8)

使上式成立，则v=e-(1/2)μ≈0.778 8，k≈0.707/η。

1.4FSWT逆变换[8]

FSWT可对分析信号进行时频分解，理论上其逆变换可采用不同形式来实现信号重构。

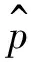
(9)

上式表明其逆变换与频率切片函数p(t)或p(ω)无关，重构信号可直接由快速傅里叶变换求得。假定信号的FSWT变换为W(t,ω,λ,σ)，任意选取时间区间(t1，t2)和频率区间(ω1，ω2)，可以得到该时频空间上的信号分量：

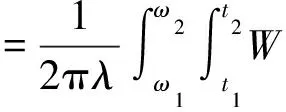
(10)

1.4 能量分布特征[9]

FSWT能方便地重构任意频带内的信号，并且不受小波基函数的限制。利用该特点，可通过构造合理的子频带，对信号进行更加详细具体的分析，进而获取信号细节特性。定义任意频带的能量为

(11)

式中，Ei,j表示信号在频率范围为[i-j]Hz的能量，xk(k=1,2,…,n)为相应频带各个采样点的幅值。

相应的总能量为

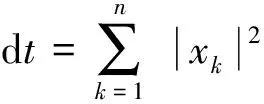
(12)

各个频带的能量占总能量的百分比为

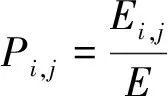
(13)

2 EMD-FSWT方法爆破振动信号分析

2.1 爆破振动信号EMD分解

图1为典型的多段微差爆破振动信号时程曲线，采样频率5 000 Hz，采样时间0.991 s，主振频率86.67 Hz，最大振速0.713 cm/s。图2为图1信号对应的功率谱密度曲线。

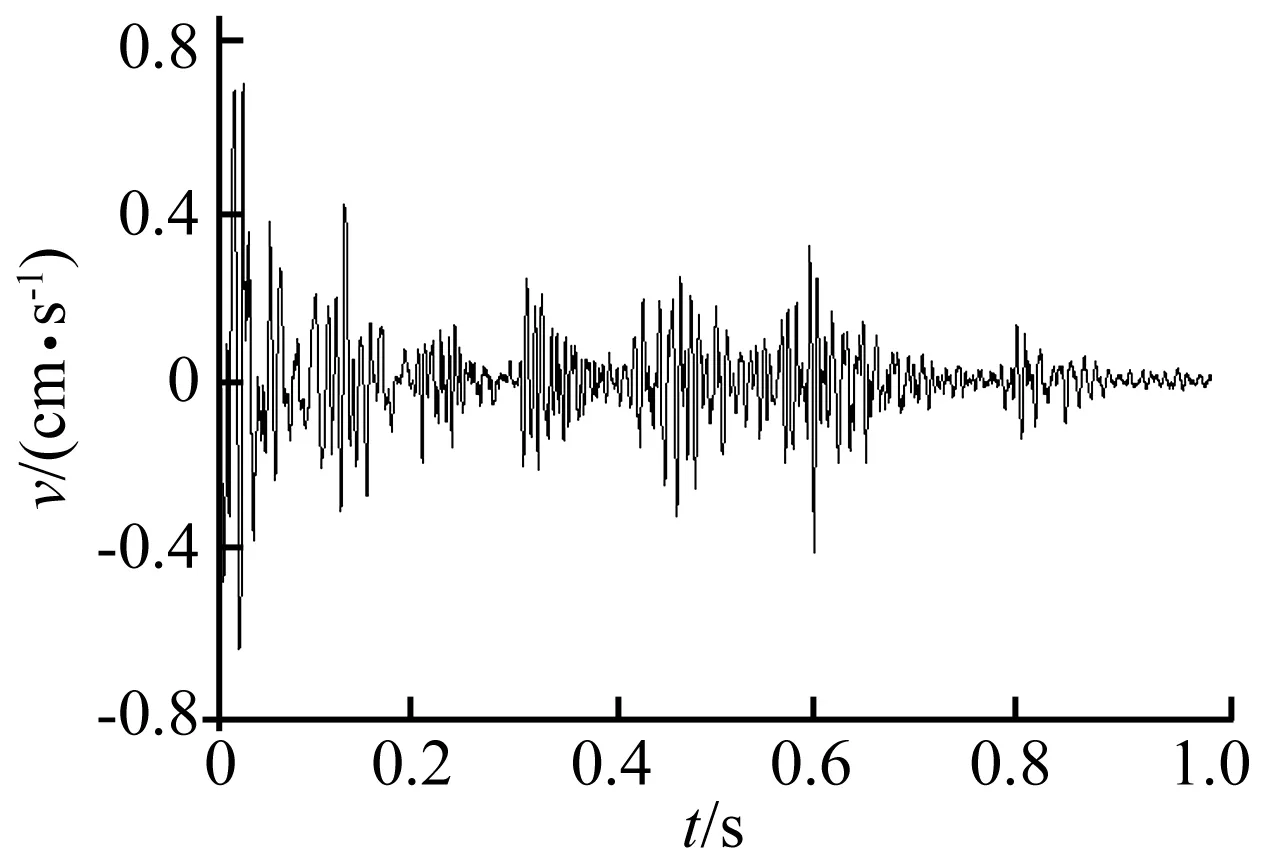
图1 爆破振动信号速度时程曲线Fig.1 Blasting vibration signal velocity curves

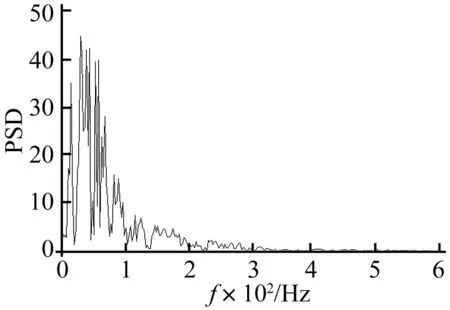
图2 爆破振动信号功率谱密度Fig.2 PSD spectrum of blasting vibration signal

EMD分解函数形式为:IMF=emd(x,t,stop,tst)，其中s为分析信号，t为信号采样时间，stop为算法判止准则，这里采用默认值为[0.05,0.5,0.05]，tst取为2，表示无停顿筛分。对图1所示原信号进行EMD分解，得到11个IMF(残余项r也作为一个IMF分量)，如图3所示。

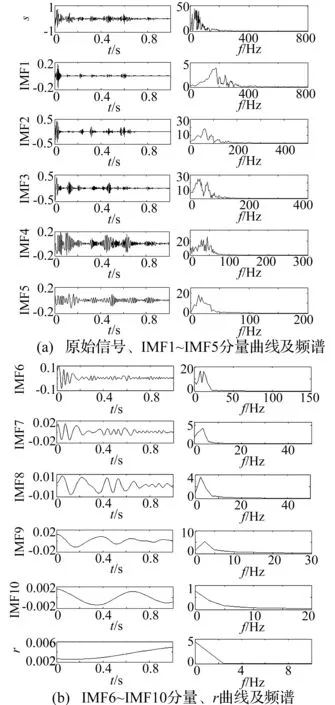
图3 原始信号、各IMF分量时程曲线及其频谱(注：s-原始信号)Fig.3 The original signal,IMF component and spectrum (Note: s-the original signal)

EMD分解是一种新的主成分分析方法[9]，它按频率从高到低提取信号本身所固有的全部模态函数，残余项r为信号微弱的变化趋势项。

2.2 优势分量确定及信号合成

信号经过EMD分解后得到的IMF分量大都具有明确的物理意义。但由于算法上的原因如插值误差、过分解等，使得EMD分解中常会出现伪分量，即与原始信号无关的分量，这些伪分量所含有的频率成分存在与信号特征频带重合的可能，应采取相关方法予以剔除[10]。文献[11]中采用了基于互相关的伪分量判定方法，通过IMF分量与原始信号之间的互相关性判定IMF的真伪，信号的主要IMF分量与原始信号的相关程度较高，而伪分量与原始信号的相关性很小。据此，从分解后各IMF分量与原始信号的相关性分析中，可以判定各IMF分量的真伪。定义分解出的各IMF分量与原始信号的互相关系数为[11]：

ρs,cj=max[Rs,cj(τ)]/max[Rs(τ)]

(14)

式中，Rs,cj为各IMF分量与原始信号的互相关，Rs(τ)为原始信号的自相关。把分解后各IMF分量与原始信号的互相关系数的大小作为评定各IMF分量是否为伪分量的指标。为了剔除信号中包含的伪分量，采用互相关性系数指标来客观评价IMF分量与原信号的相关度。互相关性系数F=CCF(s,xi,t)，其中s为原始信号，xi(i=1,2,…,n)为信号EMD分解后各IMF分量，t为信号采样时间。表1为图1爆破振动信号EMD分解得到的10个IMF分量(r分量除外)与原信号的互相关系数。

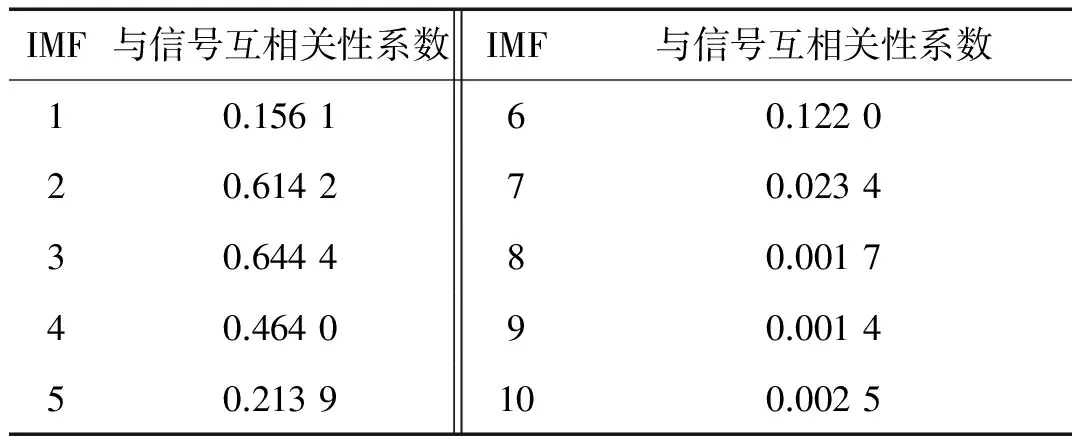
表1 各IMF分量与原信号的互相关性

从表1可知，IMF1～IMF6分量与原信号的互相关系数远大于其余阶IMF分量，可确定为信号的优势分量。因此，这里选择这几阶分量作为优势IMF分量，将其合成得到爆破振动特征信号如图4所示。

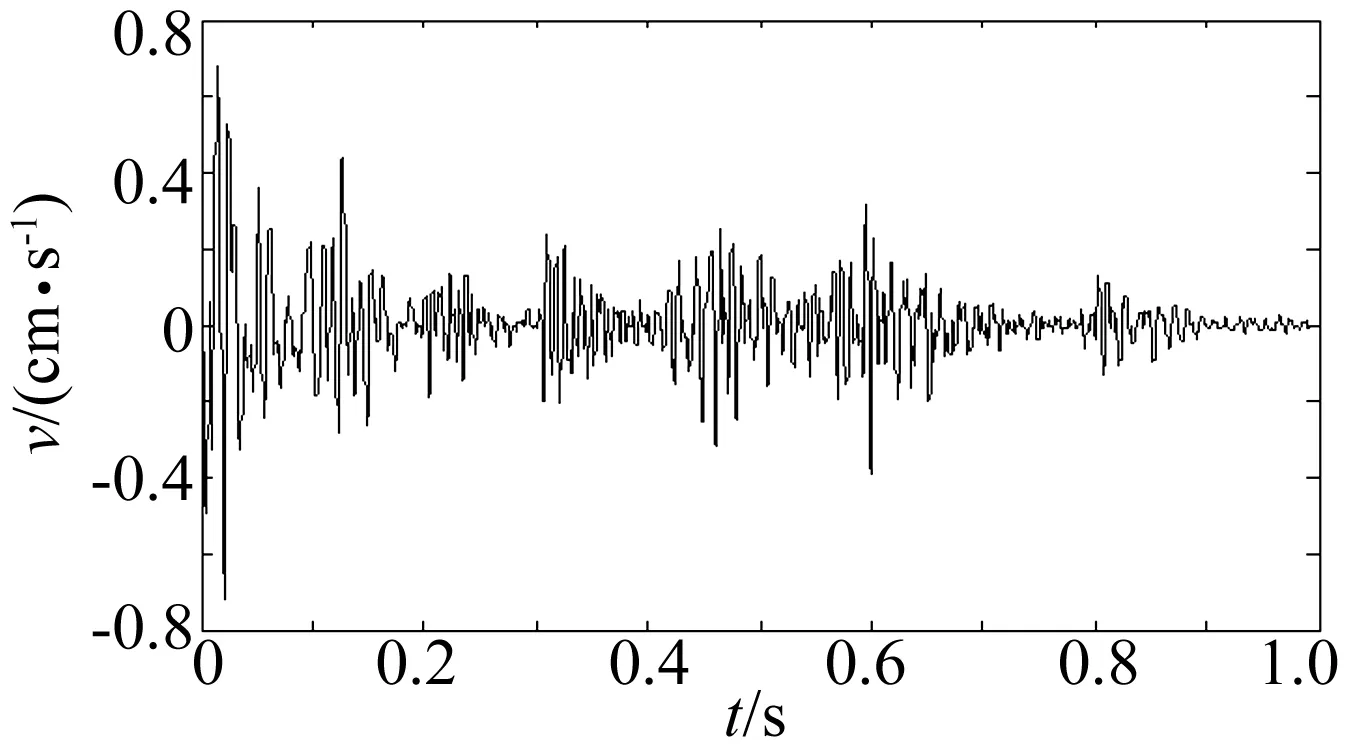
图4 优势分量合成信号Fig.4 The advantage component synthesized signal

2.3 信号特征频率精细化分析

图5 优势分量合成信号FSWT三维时频能量分布Fig.5 FSWT 3D time-frequency energy distribution of the advantage component synthesized signal

从图5可知，爆破振动信号中超过500 Hz的信号分量很小，因此可选取[0,500]Hz作为细化分析的频率切片区间。该频带区间范围内的FSWT分析结果见图6。

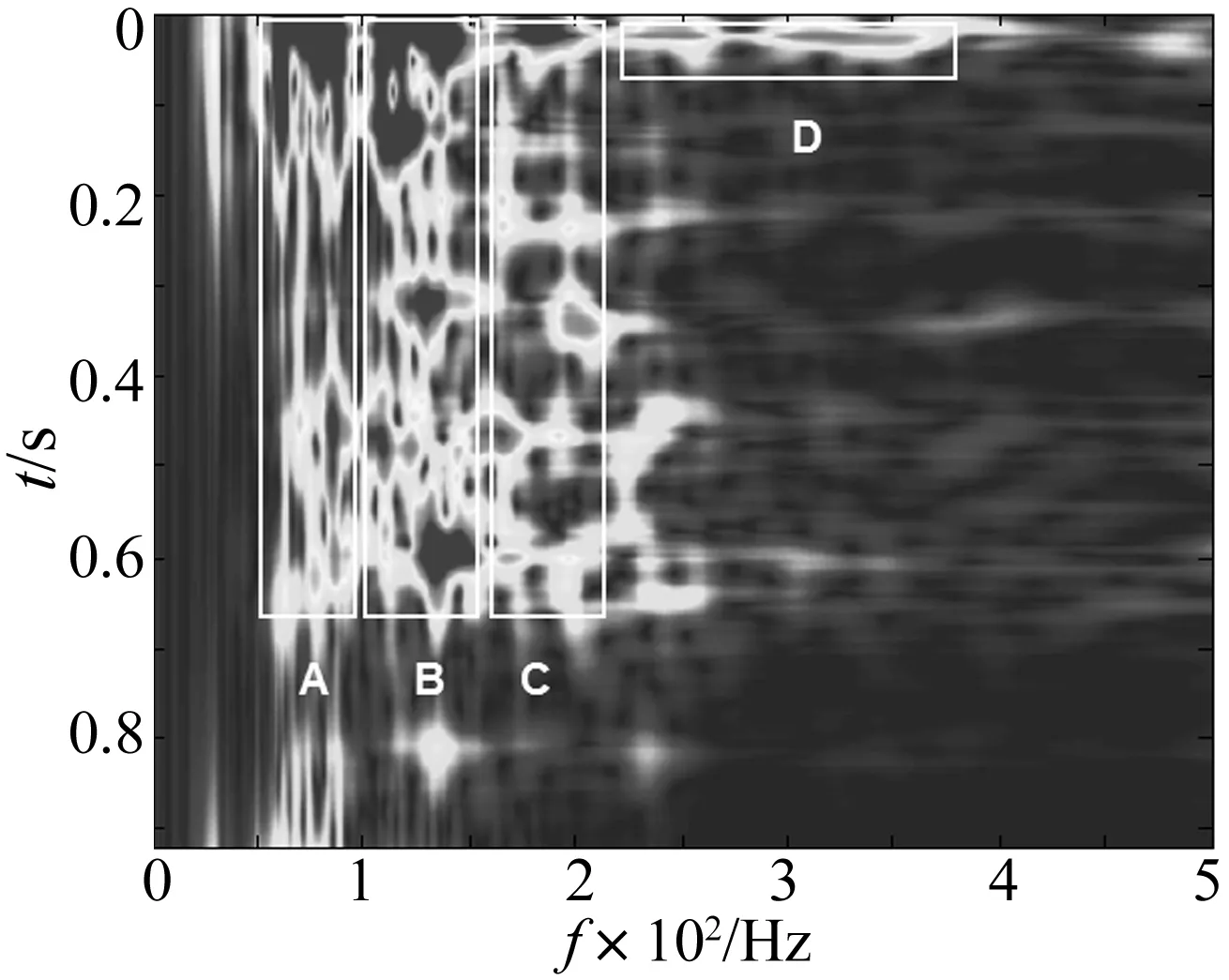
图6 合成信号[0,500]Hz FSWT结果Fig.6 [0,500]Hz FSWT of synthesized signal

从图5和图6分析中可发现：EMD优势分量合成信号时频能量谱中存在四个能量较大且持续时间较长区域，分别对应频带A：[55,90]Hz，B:[105,155]Hz，C:[160,210]Hz，D:[230,370]Hz。因此，基于EMD分解优势分量重组信号FSWT的时频分析结果，不仅能获得爆破振动信号中的频率成分，亦能获得该信号中能量幅值随时频的变化规律。

由图6中四个能量较强“色块”，提取几个能量强、频率处于该信号主要频率段内的A、B、C、D四个切片区间定义为该爆破振动信号的特征切片。为研究图1爆破振动信号在四个特征切片区间内完整的时频特征，在信号全时程范围分别在四个频率切片区间内进行细化FSWT分析，如图7所示。

图7 特征频率切片区间FSWT精细化分析Fig.7 FSWT fine analysis of characteristic frequency slice interval

从图7可以看出，在爆破地震波作用发生瞬间，信号发生突变，持续较短时间后振动响应信号能量衰减到0。四个特征切片内时频特征窄而强，且间歇出现，充分刻画出爆破振动信号的短时非平稳特征。利用1.4节中FSWT能量求解算法[13]得到该信号500 Hz频率以上能量约占信号总能量的4%，500 Hz以下频率区间能量约占96%。其中55～90 Hz频段能量占54.32%，为信号能量主要聚集区，105～155 Hz频段能量占27.38%，160～210 Hz频段能量占9.72%，230～370 Hz频段能量占2.74%，其余频段能量占1.84%，体现了爆破振动信号在四个特征切片区间内能量所占比例随着频率的升高而递减的趋势。从图7对应特征切片区间内的FSWT逆变换重构信号，可获得四个特征切片区间内爆破振动响应信号时域特征信息。四个特征切片区间内，爆破振动信号振速峰值依次为：0.462 6，0.311 5，0.189 4，0.158 5，说明对于爆破振动信号而言，其振动强度随着频率的升高不断降低。

3 组合算法与传统方法分析对比

3.1 与传统方法信号消噪效果对比

为体现EMD-FSWT组合算法在爆破振动信号特征分析中的优势，对图1原始信号分别采用EMD-FSWT组合算法、HHT、WT三种分析方法进行消噪对比研究。将2.3节得到的四个特征切片对应的特征信号波形在时域叠加，便实现了EMD-FSWT组合算法对原始信号的消噪。按照2.2节分析，此处选取信号EMD分解中IMF1～IMF6分量进行信号HHT重构和误差计算。在小波分析中，Daubechies小波系列(dbN)具有较好的紧支撑性 、光滑性及近似对称性，已成功地应用于非平稳信号问题。目前在爆破信号的处理中用得最多的是 db5 和 db8[14]。这里，选用db5作为本次分析的小波函数。本文所用爆破振动采集仪的最小工作频率为5 Hz，信号的奈奎斯特(Nyquist)频率为2 500 Hz。因此，这里将信号分解到第9层来实现信号的重构，对应的最低频带为(0～4.883) Hz,最接近采集仪的最小工作频率，保证信号分析的精度和有效性。图8为分别采用EMD-FSWT组合算法、HHT、WT小波算法对图1爆破振动信号进行消噪前后的重构信号和重构误差。

图8 EMD-FSWT、HHT、WT三种方法消噪对比及重构误差Fig.8 De-noising contrast of EMD-FSWT, HHT, WT methods and reconstruction error

为了定量研究三种算法在爆破振动信号去噪分析中的应用效果，引入均方根误差(RMSE)、信噪比(SNR)、峰值误差(PE)作为评价标准[15]：

(15)

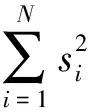
(16)

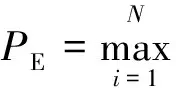
(17)

3.2 组合算法与传统时频分析对比

3.2.1 与STFT对比

STFT是以傅里叶变换为基础，最早的时频分析方法。通过对信号加时间窗并滑动后做Fourier变换，可得信号的时-频域联合分布能量谱。对爆破振动信号f(t)∈L2(R)，其STFT定义为[18]：

f(ω,τ)=∫Rf(t)g*(ω-τ)e-iωtdt

(18)

图9所示为图1中原始信号基于STFT算法所得到信号能量时频分布情况，纵坐标为归一化频率。归一化频率的转化关系为[19]：

fnormalized=f/fnyquist

(19)

式中f指不同频率值，fnyquist为信号的Nyquist频率为2 500 Hz，信号[0，500]Hz频段对应于[0，0.2]Hz归一化频率区间。

图9 原信号短时傅里叶分析 Fig.9 STFT analysis of original signal

从图9看出，爆破振动信号的能量分布主要集中在[0.01,0.2]s时间域内，频率主要集中在[0.06，0.09]Hz和[0.1，0.14]Hz归一化频率之间，能量在时、频域上聚集性差并且导致0.7 s后高段别雷管起爆能量缺失，不能完全反映爆炸冲击波时频特性。同时，在STFT中所加窗函数的宽度是固定的，这就导致其时频分辨率是固定的，缺乏细化功能。而在EMD-FSWT中，窗函数的宽度会随着分析信号的频率自适应变换，这使得信号滤波和分解在时、频域是同时进行的。与图9相比，图6、图7结果基于EMD-FSWT组合方法所得时频谱更能显示出每次由爆炸冲击产生的能量细节特征。

3.2.2 与RSPWVD对比

二次型时频分布可较准确进行时频分析。对于给定的信号f(t)，其Wigner-Ville分布可以用下式来定义[20]：

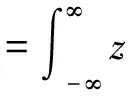
(20)

其中核函数为：φ(τ,ν)=1，式中z(t)是f(t)的解析信号。平滑Wigner-Ville分布是采用窗函数g(v)和h(τ)对信号的时域变量和频域变量进行平滑处理的能量谱，重排平滑Wigner-Ville分布(Reassigned Smoothing Pseudo Wigner-Ville Distribution,RSPWVD)是将平滑Wigner-Ville总体能量按区域重心进行重新分配得到的，更能体现信号的局部能量分布特征。图10为图1中对应爆破振动信号的RSPWVD分布。

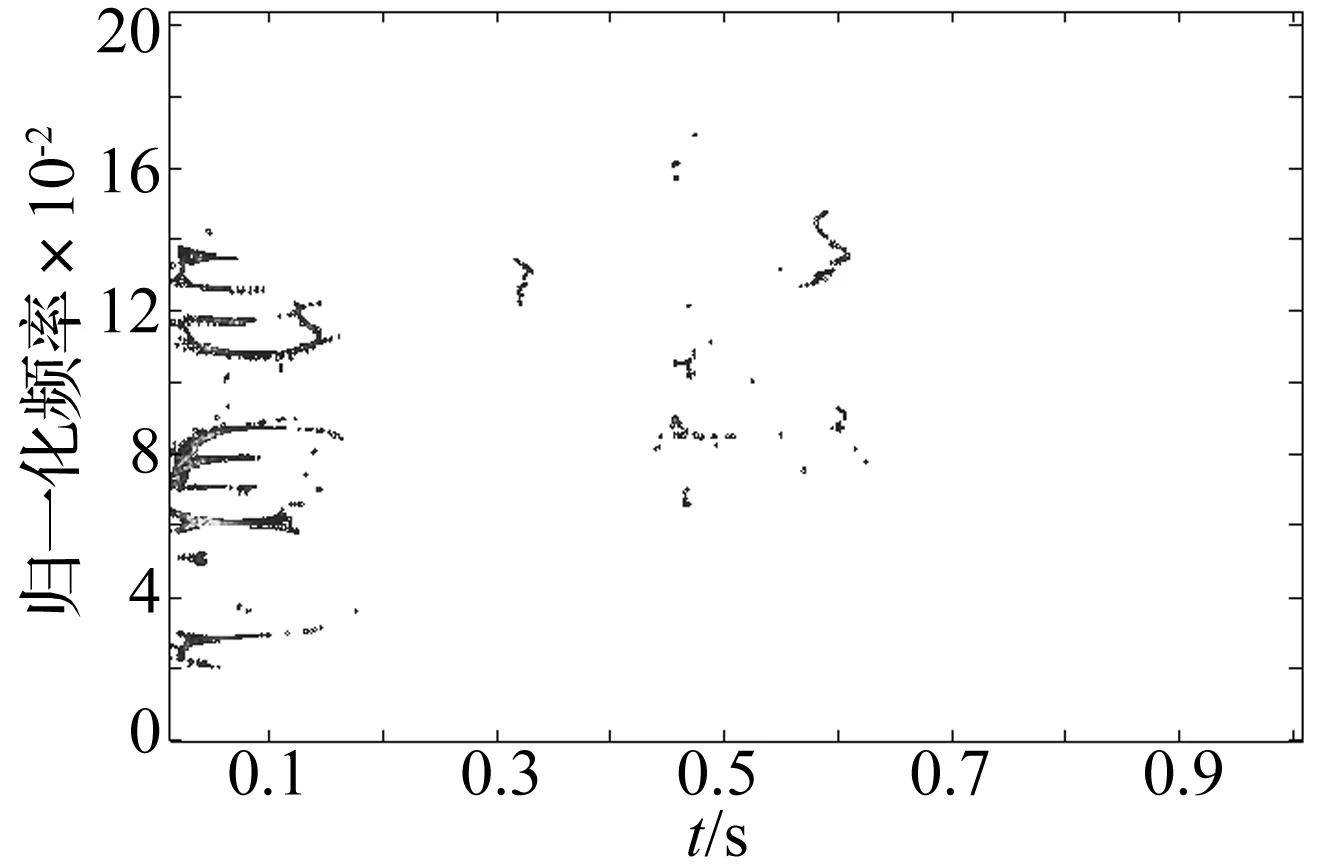
图10 原信号重排光滑Wigner-Ville分布Fig.10 RSPWVD of original signal

将图6、图7与图10对比分析发现，RSPWVD能量谱虽能在一定程度上体现该爆破振动信号所含时频特征，但图10显示其聚集性不高，仍未能准确显示该爆破振动信号能量分布。同时，由于RSPWVD算法对含多频率成份信号分析时因算法本身缺陷，导致变换过程中对噪声成分较为敏感并会产生严重的交叉项和模态混叠现象，对时频分析结果带来不利影响，使其应用受到很大限制。

4 结 论

(1)本文提出了基于EMD-FSWT组合爆破振动信号分析方法。利用组合分析技术获取振动信号在全频带时频分布特征，按能量分布细化特征频率切片区间，可以得到更加直观、分辨率更高的信号时频特征。

(2)通过EMD-FSWT频率切片区间能量计算，得到了四个切片区间能量百分比随着频率增大而递减的趋势。同时，其振动强度随着频率的升高也具有相同的规律。

(3)FSWT逆变换实现了EMD分解优势分量合成信号的重构去噪，并与HHT、WT方法去噪效果进行对比，证明了EMD-FSWT组合算法可满足爆破振动信号的高精度消噪和滤波要求。与短时Fourier(STFT)、重排平滑Wigner-Ville分布(RSPWV)两种传统时频分析方法对比，表明了EMD-FSWT组合算法可实现动态尺度变换，运算结果体现出良好的时频聚集性，适宜于精细化描述爆破振动信号的时频特征。

[1] 李舜酩,郭海东,李殿荣. 振动信号处理方法综述[J]. 仪器仪表学报,2013,34(8):1907-1915. LI Shunming,GUO Haidong,LI Dianrong.Review of vibration signal processing methods [J]. Chinese Journal of Scientific Instrument,2013,34(8):1907-1915.

[2] 赵迎,乐友喜,黄健良,等.CEEMD与小波变换联合去噪方法研究[J].地球物理学进展,2015,30(6):2870-2877. ZHAO Ying,LE Youxi,HUANG Jianliang,et al.CEEMD and wavelet transform jointed de-noising method[J].Progress in Geophysics,2015,30(6):2870-2877.

[3] YAN Z, MIYAMOTO A, JIANG Z. Frequency slice wavelet transform for transient vibration response analysis [J]. Mechanical Systems and Signal Processing, 2009,23(5): 1474-1489.

[4] 郭涛,方向,谢全民,等. 频率切片小波变换在爆破振动信号时频特征精确提取中应用[J]. 振动与冲击,2013,32(22):73-78. GUO Tao,FANG Xiang,XIE Quanmin,et al.Application of FSWT in accurate extraction of time-frequency features for blasting vibration signals [J]. Journal of Vibration and Shock, 2013,32(22):73-78.

[5] 汤宝平,钟佑明,程发斌．基于 HHT 的非平稳信号分析仪的研究[J]．仪器仪表学报,2007,28(1): 29-33． TANG Baoping,ZHONG Youming,CHENG Fabin.Research on nonstationary signal analyzer based on HHT[J]．Chinese Journal of Scientific Instrument,2007,28(1): 29-33．

[6] YAN Z, MIYAMOTO A, JIANG Z.Frequency slice algorithm for modal signal separation and damping identification [J]. Computers and Structures,2011, 89(1/2):14-26.

[7] 张宇辉,刘梦婕,黄南天,等. 频率切片小波变换在局部放电信号分析中的应用[J]. 高电压技术,2015,41(7): 2283-2293. ZHANG Yuhui, LIU Mengjie, HUANG Nantian,et al.Application of frequency slice wavelet transform in partial discharge signal analysis [J].High Voltage Engineering,2015,41(7):2283-2293.

[8] 段晨东,高强,徐先峰. 频率切片小波变换时频分析方法在发电机组故障诊断中的应用[J]. 中国电机工程学报,2013,33(32):96-103. DUAN Chendong,GAO Qiang,XU Xianfeng.Generator unit fault diagnosis using the frequency slice wavelet transform time-frequency analysis method[J]. Proceedings of the CSEE, 2013, 33(32): 96-103.

[9] 赵国彦,邓青林,马举. 基于FSWT时频分析的矿山微震信号分析与识别[J]. 岩土工程学报,2015,37(2):306-312. ZHAO Guoyan,DENG Qinglin,MA Ju.Recognition of mine microseismic signals based on FSWT time-frequencyanalysis [J].Chinese Journal of Geotechnical Engineering, 2015,37(2):306-312.

[10] 李成武,解北京,杨威,等. 基于HHT法的煤冲击破坏SHPB测试信号去噪[J]. 煤炭学报,2012,37(11):1796-1802. LI Chengwu,XIE Beijing,YANG Wei,et al.Coal impact damage SHPB testing signal de-noising based on HHT method [J].Journal of China Coal Society,2012,37(11):1796-1802.

[11] 李精明,魏海军,魏立队,等.摩擦振动信号的经验模式分解和多重分形研究 [J]. 振动与冲击, 2016, 35(3): 198-203. LI Jingming,WEI Haijun,WEI Lidui,et al.Empirical mode decomposition and multifractal of frictional vibration signal[J].Journal of Vibration and Shock,2016, 35(3): 198-203.

[12] 邹云屏,李 潇. 信号变换与处理[M]. 武汉：华中理工大学出版社,1993:8-12.

[13] 庞学苗,李建伟,邢宗义,等. 基于频率切片小波变换的轨道列车轮对振动信号分析[J]. 铁道机车车辆,2015,35(增刊1):26-31. PANG Xuemiao,LI Jianwei,XING Zongyi,et al.Analysis of wheel-rail vibration signal based on frequency sliced wavelet transform [J].Railway Locomotive & Car,2015,35(Sup1):26-31.

[14] 何浩祥,陈奎,闫维明. 基于小波包变换和时变频率的结构地震损伤评估[J]. 振动与冲击,2016,35(7):23-30. HE Haoxiang,CHEN Kui,YAN Weiming.Structural seismic damage assessment based on wavelet packet transformation and time-varying frequencies[J]. Journal of Vibration and Shock,2016,35(7):23-30.

[15] 谢全民,龙源,钟明寿,等. SGWT在爆破振动信号信噪分离中的应用研究[J]. 振动与冲击,2012,31(1):24-28. XIE Quanmin,LONG Yuan,ZHONG Mingshou,et al.Application of SGWT in separation of noises from a blast vibration signal[J]. Journal of Vibration and Shock, 2012, 31(1):24-28.

[16] 路亮,龙源,谢全民,等. 爆破振动信号的提升小波包分解及能量分布特征[J]. 爆炸与冲击,2013,33(2):140-147. LU Liang,LONG Yuan,XIE Quanmin,et al.Decomposition and energy distribution of blasting vibration signal based on second generation wavelet packet(SGWP) [J]. Explosion and Shock Waves,2013,33(2):140-147.

[17] 王姣,李振春,王德营.基于CEEMD 的地震数据小波阈值去噪方法研究[J].石油物探,2014,53(2):164-171. WANG Jiao，LI Zhenchun，WANG Deying. A method for wavelet threshold denoising of seismic data based on CEEMD [J].Geophysical Prospecting for Petroleum,2014,53(2): 164-171.

[18] 郭远晶,魏燕定,周晓军. 基于STFT时频谱系数收缩的信号降噪方法[J]. 振动、测试与诊断,2015,35(6):1090-1096. GUO Yuanjing,WEI Yanding,ZHOU Xiaojun.Signal denoising method based on STFT time-frequency spectrum coefficients shrinkage [J]. Journal of Vibration,Measurement & Diagnosis,2015,35(6):1090-1096.

[19] 张艳博,梁鹏,刘祥鑫,等. 基于多参量归一化的花岗岩巷道岩爆预测试验研究[J]. 岩土力学,2016,37(1):96-104. ZHANG Yanbo,LIANG Peng,LIU Xiangxin,et al.An experimental study of predicting rockburst in granitic roadway based on multiparameter normalization [J].Rock and Soil Mechanics,2016,37(1):96-104.

[20] 赵明生,张建华,易长平. 基于小波分解的爆破振动信号RSPWVD二次型时频分析[J]. 振动与冲击,2011,30(2):44-47. ZHAO Mingsheng,ZHANG Jianhua,YI Changping.Blasting vibration signal RSPWVD quadratic time-frequency analysis based on wavelet decomposition[J]. Journal of Vibration and Shock, 2011, 30(2): 44-47.

Application of EMD and FSWT combination method in blasting vibration signal analysis

YANG Renshu, FU Xiaoqiang, YANG Guoliang, CHEN Jun, CHEN Wei

(School of Mechanics and Civil Engineering，China University of Mining and Technology(Bei jing), Beijing 100083, China)

In view of the shortcomings of the traditional empirical time-frequency analysis methods, a blasting vibration signal analysis method based on EMD-FSWT was proposed. The EMD of blasting vibration signals collected in actual engineering was carried out,according to the correlation coefficient, to determine the dominant component and reconstruct the signal, and the full band FSWT time-frequency characteristics of the reconstructed signal were then provided. In virtue of the characteristic of the inverse transformation of FSWT, that any frequency range of the signal can be cut out, the time and frequency ranges of the reconstructed signal were chosen and more refined time-frequency feature extraction was achieved. The filtering de-noising effects of the EMD-FSWT combination method, Hilbert Huang transform (HHT) and wavelet transform (WT), were analysed and compared with those of two traditional methods, the short time Fourier transform (STFT) and rearrangement smooth Wigner-Ville distribution (RSPWVD).The analysis results show that: the EMD-FSWT combination method has higher time-frequency domain resolution in transient signal analysis. Its de-noising and filtering effect is good and is more suitable for precise time-frequency characteristics analysis for the blasting vibration signal.

blasting vibration; empirical mode decomposition (EMD); frequency slice wavelet transform (FSWT); time-frequency analysis; energy distribution

国家自然科学基金-面上项目(51274203)

2016-03-08 修改稿收到日期：2016-05-05

杨仁树 男，博士，教授，博士生导师，1963年10月生

付晓强 男，博士生，1984年8月生 E-mail:fuxiaoqiang1984@163.com

TD235.1

A

10.13465/j.cnki.jvs.2017.02.009