黄土边坡降雨入渗规律及其对稳定性的影响
2017-02-13张建忙
汪 勇,刘 瑾,张建忙
(河海大学地球科学与工程学院,南京 210098)
黄土边坡降雨入渗规律及其对稳定性的影响
汪 勇1,刘 瑾1,张建忙1
(河海大学地球科学与工程学院,南京 210098)
降雨是诱发土质边坡失稳的主导因素之一,研究降雨入渗对土质边坡稳定性的影响有着重要意义。以陕西富平地区某黄土边坡为例,结合野外现场试验和数值模拟,研究了降雨入渗规律和其对稳定性的影响。研究结果表明,降雨入渗的影响范围在边坡浅层,深度为2~2.5 m。土体的抗剪强度参数受含水率影响较大,在雨水入渗条件下,边坡表层的孔隙水压力变化较大,孔隙水压力的变化区域指示着湿润锋的位置。最大剪应力的应力集中区域为湿润锋区域以及各级边坡坡脚处,降雨后边坡稳定性系数比降雨前降低了12%,显示降雨对边坡的稳定性影响较大。
降雨入渗;黄土边坡;人工降雨;数值分析;稳定性
0 引言
边坡稳定性问题一直是岩土工程的一个重要课题。统计资料表明,边坡失稳破坏的最主要诱发因素是降雨入渗[1-2]。随着高速公路以及铁路的发展,降雨对边坡的影响越来越受到重视,降雨入渗引起的非饱和土边坡失稳每年给国家社会造成巨大的经济损失[3-4],因此对降雨入渗下的边坡稳定性进行研究很有必要。土质边坡在天然状况下一般处于非饱和态,对于降雨条件下的非饱和土边坡研究成为学者研究的重点。近年来,国内很多学者开展了关于降雨入渗对土质边坡的作用机理、影响因素与稳定性影响的研究,研究的结果表明,边坡稳定性不仅与渗透系数相关,也与降雨历时有关。在渗透过程中,非饱和带基质吸力与含水率的密切相关,含水率的提高导致孔隙水压力升高,基质吸力较小,土体的抗剪强度也会随之变化,当降雨强度与降雨历时达到一定值后,边坡可能出现滑坡等地质灾害[5-10]。常金源、李宁以Green-Ampt入渗模型为基础,建立降雨条件下浅层滑坡的概念模型,既考虑了边坡坡面倾斜的影响,也考虑了非饱和土的特性[11-12]。蒋中明等提出降雨入渗导致边坡表层会出现暂态饱和区并形成暂态水压力,并推导了边坡潜在滑动面位于暂态饱和区与非饱和区两种情形下的安全系数计算方法[13]。在降雨入渗过程中,耦合作用同样影响边坡稳定性。李海亮等针对黄土的非均质性开展研究,考虑渗流场与应力场耦合作用[14],程彬等也做了渗流场与应力场耦合的相关工作[15]。夏元友运用水气两相流与应力耦合的方法研究边坡稳定性[16]。
本文以陕西富平地区地质环境下的典型黄土边坡为研究对象,分析人工降雨入渗深度和土体含水率的变化规律,并对降雨中孔隙水压力、最大剪应力以及稳定性进行数值模拟,为今后研究黄土边坡失稳及其防治提供参考依据。
1 试验区概况
富平县位于陕西省中部,属大陆性温带半干旱、半湿润气候区,四季干湿冷暖分明。冬季气候寒冷,干燥少雨雪;春季温度回升快,气候日差较大,易出现大风、浮尘等寒潮降温天气,常有春旱发生;夏季气温高,雨量集中,但降水时空分布不匀,常有伏旱发生;秋季较凉爽、湿润,多连阴雨,气温下降较快。年降水量为520 mm左右,主要集中于夏季和秋季,分别占年降雨量的42%和31%[17]。
试验所选边坡位于富平县县城近西北方向约5 km处,在底店乡底店村附近,边坡具体平面位置图如图1所示。道路工程是富平县底张二级路县城段,项目由陕西秦正建设集团于2011年4月开始进行勘察设计并建设,富平县公路管理局在现场进行监理,于2012年12月正式竣工。
图1 平面位置图Figure1 Plan position
试验所选边坡为人工开挖边坡,坡高18 m,边坡分3级,单级坡高为6 m,下面两级坡比为1∶0.75,最上面一级坡比为1∶1。
2 野外试验与数据测定
研究采用野外现场试验和室内试验分析相结合的研究方法,主要分析降雨前后土体物理力学特性及降雨入渗对土质边坡稳定性的影响。
(1)野外试验:2011年6月,由陕西秦正建设集团设计和实施野外试验,地点在公路边坡附近,其形态与实际边坡类似,大小与实际边坡比例为1∶3。按实际的坡面线进行刷坡,以保证土体在雨水入渗时有相同的密实度和含水率。降雨模拟装置由框架式降雨器、供水桶、管线以及控制阀门等组成。利用降雨器对不同高度和不同强度下的雨滴变化进行研究,降雨高度超过2.5 m时,不同强度下的雨滴较接近。该降雨器具有较好的稳定性,降雨分布较为均匀,可持续性好,满足实验要求。因此,野外试验的降雨器在边坡上方2.5 m处安置。根据气象部门对降雨量等级的划分,试验的降雨强度等级为小到中雨,降雨量为0.008 m/h,降雨时长12 h。
(2)取样:在降雨试验过程中,试验人员分组取样,每次取完土样后迅速用保鲜袋密封(防止水分蒸发),带回实验室立即进行土体物理力学试验。取样时间点按设计试验方案为0(即降雨前)、2、4、6和12 h,取样深度根据实际情况,每隔0.5 m取样,深度到达2.5 m,每组样重复取3次。
(3)数据测定:本实验是在实际边坡的旁边进行模拟实验,黄土的物理性质与边坡工程所在地的实际物理性质相同,土体含水率测定采用烘干法,土体力学性质测定采用抗剪试验,仪器选用烘箱、应变控制式直剪仪等进行了有关参数的测定,测得的含水率及抗剪强度参数作为边坡模拟的物理力学参数,取得重复样的平均值,具体参数见表1,然后采用GeoStudio软件进行渗流场和应力场耦合模拟边坡在降雨过程中的变化情况。

表1 土样物理力学参数Table 1 Soil sample physical and mechanical parameters
3 降雨入渗规律及其对稳定性的影响
3.1 降雨入渗规律
在降雨强度一定的情况下,降雨时间越长,土体含水率的变化越大,降雨入渗的深度也会随之增大。对于同一深度的土层,其含水率随入渗时间的增加而增加,且土层深度越深,含水率变化的幅度越小。从图2中可以看出,1 m深度以上土层在入渗时间4 h内,其含水率急剧增加,4 h后随雨水入渗其含水率变化趋势逐步缓慢,是由于表层土体的含水率接近饱和,基质吸力趋近于0,雨水入渗较慢;1 m深度以下的土层,降雨时间达到6 h后含水率才出现缓慢增加的趋势。
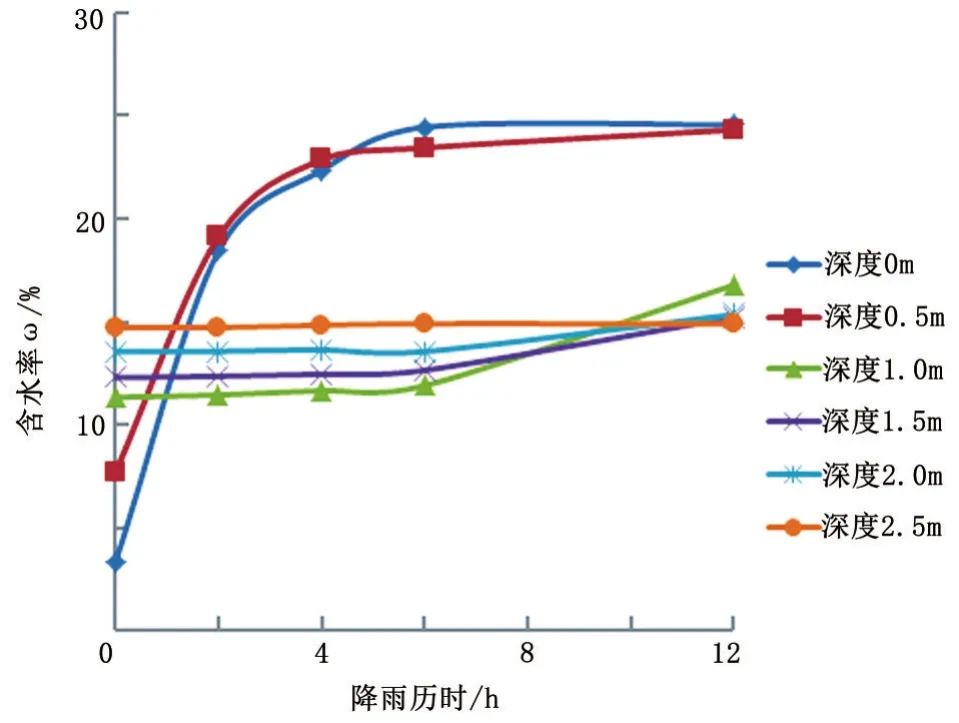
图2 不同深度土体含水率与降雨时间的关系Figure 2 Relationship between different depth soil mass specific moisture content and rainfall time
从图2同样可以看出,深度为2.5 m处的土体含水率几乎没有随着降雨时间的变化而变化,由此可以推断降雨入渗的影响深度为2~2.5 m,再往下不再是降雨入渗的影响范围,属于边坡浅层,降雨入渗造成的滑坡大多数也为浅层滑坡。
3.2 稳定性影响
3.2.1 降雨入渗对土体抗剪强度的影响
土体含水率测试试验与抗剪试验的结果如图3和图4。天然结构黄土的黏聚力C在低饱和度情况下对含水率ω的变化很敏感,当含水率从3%增加到25%时,黏聚力C从67 kPa降低到14 kPa,减少了4倍多;当含水率ω大于20%后,黏聚力C随含水率ω的变化明显小于20%之前。而天然黄土边坡的内摩擦角受降雨影响较小,当含水率从3%增加到25%时,内摩擦角从30°降低到25°,变化范围较小。

图3 土体含水率与粘聚力的关系Figure 3 Relationship between soil mass specific moisture content and cohesion

图4 土体含水率与内摩擦角的关系Figure 1 Relationship between soil mass specific moisture content and internal friction angle

图5 网格划分与边界条件Figure 5 Grid division and boundary condition
3.2.2 数值模拟
3.2.2.1 模型建立
本文运用GeoStudio软件进行模拟,结合试验边坡的地形特征建立建立几何模型。考虑到降雨渗流会引起边坡内应力分布的变化,故选用该软件中的Seep模块、Sigma模块以及Slope模块,基于边坡渗流场与应力场的耦合分析边坡的稳定性。网格划分采用三角形和四边形混合的非结构化网格,共划分2445个单元。模拟计算时只考虑自重应力和渗透作用,模型底面边界施加水平方向和垂直方向的位移约束,左右两侧边界均施加水平方向的位移约束,网格划分与边界条件如图5。在有限元分析时假设试验区边坡的受力及变形视为平面应变问题,屈服准则采用Mohr-Coulomb准则;模拟时考虑入渗过程,雨水入渗时边坡的物理力学指标发生变化,并视试验区坡体为均质黄土,进行降雨过程中不同时间点边坡位移、应力的模拟对比,分析雨水入渗对边坡稳定性的影响。
本文中考虑到渗流场与应力场的耦合作用,在渗流过程中,体积含水量的变化会导致基质吸力的变化,渗透系数与体积含水量、基质吸力均有关系,在Seep模块中选用Van Genuchten方法来确定渗透系数与基质吸力的关系,从而确定渗透性函数。本次研究降雨历时12 h,降雨强度恒定为0.008 m/h,时间步长为2 h。
3.2.2.2 模拟结果分析与评价
①孔隙水压力分析。在本次研究时间范围内,入渗雨水主要集中在边坡浅层,坡下部土层受降雨入渗影响小,因此重点对表层内的孔隙水压力变化进行分析。图6为降雨时间分别为0、2 h、6 h和12 h边坡内部孔隙水压力的等值云图。
从图6中可以看出,沿高程线性变化,表层内孔隙水压力均为负值。在降雨前,孔隙水的变化随着高程线均匀变化,在降雨2 h后,坡面孔隙水压力小于零,这是因为降雨强度与饱和土渗透系数十分接近且小于土壤允许入渗的容量。而当降雨时间达到6 h后,入渗的雨水使得表层上部土体趋于饱和,孔隙水压力迅速增大,基质吸力逐渐消失,而孔隙水压力变化较大区域就是降雨入渗时湿润锋的深度。随着降雨的进行,湿润锋深度不断增加,同一深度位置的孔隙水压力随时间增加而增大,湿润锋位置以下土层内孔隙水压力不变化,说明下部土层几乎不受降雨的影响。同时也可以看出边坡表面的孔隙水压力等值线出现了一定的密度集中,边坡上部的孔隙水压力变化明显大于边坡底部。

图6 降雨过程中坡体孔隙力压力等值云图(kPa)Figure 6 Slope mass pore pressure contour nephogram during rainfall process(kPa)
②最大剪应力特征。由模拟结果可知,在自重应力和渗流作用下,试验区边坡降雨前后坡体最大剪应力随坡体深度的增加,其应力逐步增大。从图7可以看出,在自重应力与渗流作用的作用下,边坡表层应力等值线密集,尤其在在各级坡脚处最密,出现应力集中带。结合孔隙水压力变化曲线分析得出的湿润锋位置可知,应力密集带出现在湿润锋深度附近,表明边坡易发生沿湿润锋的浅层破坏。
③稳定性系数的变化特征。在降雨的过程中,随着雨水渗入,坡体内部的土体含水率逐渐增加,导致抗剪强度降低,另外渗流场的作用也会降低边坡的稳定性。从图7稳定性系数变化的过程来看,边坡的稳定性系数从降雨前的1.581,在降雨过程中不断减小,12 h后降到1.34。由图8也可看出,在降雨过程中,边坡的稳定性系数出现短暂时间内的升高,可能是由于其表层以下的含水率较低,渗透系数较小,在边坡表层形成暂态饱和区,重力增加,而之后表面形成径流,内部雨水逐渐渗透,稳定性系数又逐渐降低,虽然降雨前后边坡均处于稳定状态,但稳定性系数下降了18%左右,且有继续降低的趋势,甚至产生滑坡,说明降雨入渗对边坡的稳定性影响明显。
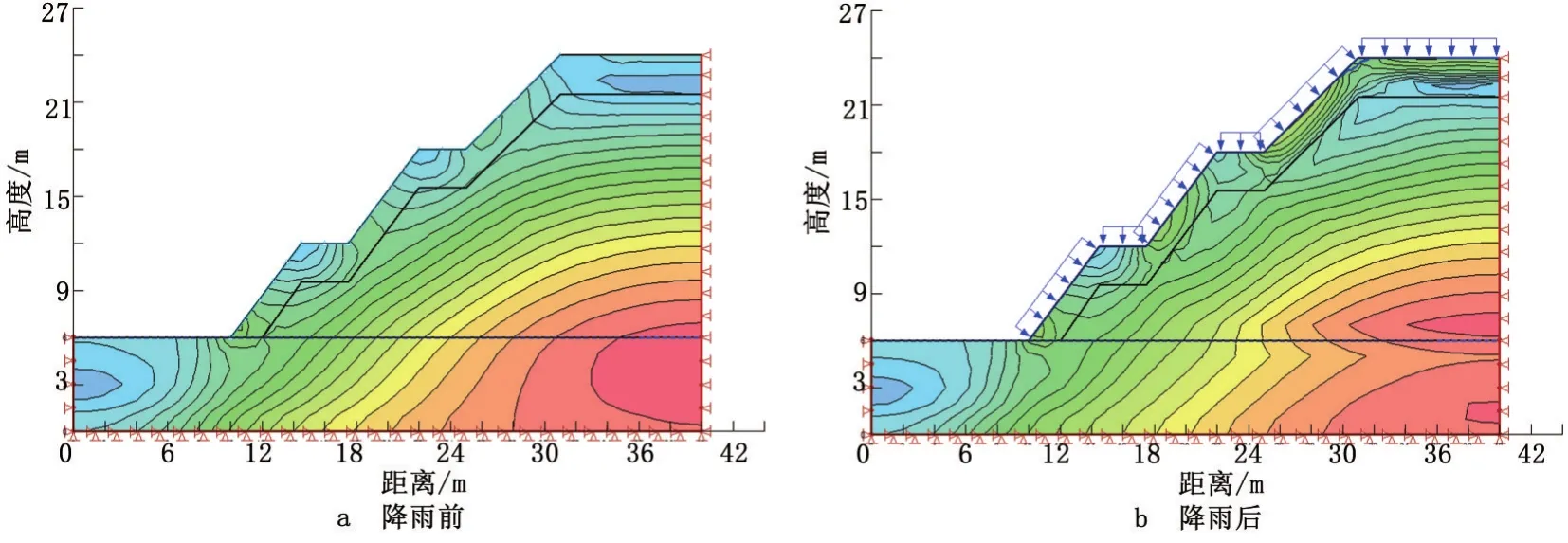
图7 降雨前后坡体应力等值云图(kPa)Figure 7 Slope mass stress contour nephogram before and after rainfall(kPa)

图8 稳定性系数与降雨时间的关系Figure 8 Relationship between stability coefficient and rainfall time
4 结论
降雨入渗对于黄土边坡的影响较大,尤其是边坡浅层土物理力学性质的变化,对边坡的稳定性的影响较大。
(1)降雨入渗的影响深度范围为2~2.5 m,在降雨过程前期边坡表层土层含水率急剧增加,而后其含水量变化趋势逐步缓慢,边坡深部的含水率在降雨一段时间后才出现缓慢增加的趋势。
(2)土体的抗剪强度参数受含水率影响较大,尤其是土体粘聚力C,含水率的变化会引起黏聚力C很大程度的变化,而内摩擦角随含水量的变化呈缓慢减小趋势。
(3)在雨水入渗条件下,边坡表层的孔隙水压力在表层变化较大,孔隙水压力的变化区域指示着湿润锋的位置。最大剪应力的应力集中区域为湿润锋区域以及各级边坡坡角处,降雨后边坡稳定性系数比降雨前降低了12%,降雨对边坡的稳定性影响较大。
[1]周家文,徐卫亚,邓俊晔,等.降雨入渗条件下边坡的稳定性分析[J].水利学报,2008,39(9):1066-1073.
[2]徐兴华,尚岳全,唐小明,等.降雨作用及坡脚开挖激发路堑滑坡的灾变效应[J].中国地质灾害与防治学报,2013,24(4):6-15.
[3]刘俊新,刘育田,胡启军.非饱和地表径流-渗流和流固耦合条件下降雨入渗对路堤边坡稳定性研究[J].岩土力学,2010,31(3):903-910.
[4]王叶娇,曹玲,武加恒.降雨入渗下非饱和土边坡稳定性影响研究[J].中外铁路,2013,33(2):25-30.
[5]言志信,高刚,于换小,等.降雨入渗条件下非饱和土边坡稳定性数值分析[J].铁道建筑,2013,7:85-88.
[6]童龙云,简文星.考虑降雨入渗过程的非饱和边坡稳定性分析[J].武汉理工大学学报,2012,34(11):78-83.
[7]张绪涛,张强勇,李术才.降雨入渗影响下的边坡稳定性分析[J].人民长江,2008,39(1):83-90.
[8]陈善雄,陈守义.考虑降雨的非饱和土边坡稳定性分析方法[J].岩土力学,2001,22(4):447-450.
[9]陈芳,田凯.降雨入渗作用下土质斜坡稳定性的数值分析[J].长江科学院院报,2013,30(12):69-73.
[10]付建新,谭玉叶,宋卫东.考虑二维降雨入渗的非饱和土边坡稳定性分析[J].东北大学学报(自然科学版),2014,35(11):1646-1649.
[11]常金源,包含,伍法权,等.降雨条件下浅层滑坡稳定性探讨[J].岩土力学,2015,36(4):995-1001.
[12]李宁,许建聪,钦亚洲.降雨诱发浅层滑坡稳定性的计算模型研究[J].岩土力学,2102,33(5):1485-1490.
[13]蒋中明,伍忠才,冯树荣,等.考虑暂态饱和区的边坡稳定性极限平衡分析方法[J].水利学报,2015,46(7):773-782.
[14]李海亮,黄润秋,吴礼舟,等.非均质土坡降雨入渗的耦合过程及稳定性分析[J].水文地质工程地质,2013,40(4):70-76.
[15]程彬,卢靖.基于GeoStudio的边坡渗流场与应力场耦合分析[J].山西建筑,2010,36(3):146-147.
[16]夏元友,张亮亮.考虑降雨入渗影响的边坡稳定性数值分析[J].公路交通科技,2009,26(10):27-32.
[17]张岁岐,辛小桂.富平县农业气候资源及灾害天气分析[J].水土保持研究,1999,6(1):32-36.
Loess Slope Rainfall Influent Seepage Pattern and Its Impact on Slope Stability
Wang Yong,Liu Jin and Zhang Jianmang
(School of Earth Science and Engineering,Hohai University,Nanjing,Jiangsu 210098)
Rainfall is one of leading factors to induce soil slope instability.Study of impact on soil slope stability from rainfall influent seepage has great significance.Taking a loess slope in Fuping area,Shaanxi as example,combined with field site tests and numerical simulation,studied rainfall influent seepage pattern and its impact on slope stability.The result has shown that the impacting extent is confined within slope superficial zone with depth 2~2.5m.Soil mass shear resistance parameters are largely impacted by specific moisture content.Under the rainfall influent seepage,slope superficial zone pore water pressure varied largely,pore water pressure variation domain indicating wetting front position.Maximum shear stress concentration regions are wetting front region and toes of slope at all levels.Slope stability coefficient after rainfall has 12%less than before rainfall,indicated larger impact on slope stability from rainfall.
rainfall influent seepage;loess slope;artificial rainfall;numerical analysis;stability
P642.22
A
10.3969/j.issn.1674-1803.2017.01.10
1674-1803(2017)01-0048-05
汪勇(1993—),男,安徽芜湖人,硕士研究生,主要研究滑坡治理与生态护坡技术。
2016-07-27
责任编辑:樊小舟
