步态识别的小波去噪质量评价方法*

涂斌斌， 谷丽华， 许 会

(1. 沈阳工业大学 信息科学与工程学院， 沈阳 110870； 2. 沈阳大学 信息工程学院， 沈阳 110044)

步态识别的小波去噪质量评价方法*

涂斌斌1，2， 谷丽华1， 许 会1

(1. 沈阳工业大学 信息科学与工程学院， 沈阳 110870； 2. 沈阳大学 信息工程学院， 沈阳 110044)

针对步态加速度信号由于采集信号包含大量尖峰或突变等高频噪声，导致在步态分析、周期划分和特征提取方面存在困难的问题，提出了一种利用小波去噪质量评价来对加速度信号小波去噪的最优参数进行选择的新方法.根据质量评价指标的几何和物理意义，使用评价指标值来指导小波去噪最优小波分解与重构层数的参数选择.当评价指标值取最小值时，其对应分解层数为最优分解层数，采用的小波基函数为最优小波基函数.结果表明，本文方法在步态识别领域可以为步态信号小波去噪选择最优小波基函数和分解层数提供理论依据.

步态； 步态识别； 加速度信号； 小波去噪； 质量评价； 小波基函数； 分解与重构； 最优参数

近些年，随着便携式及可穿戴式智能设备的快速发展，基于加速度传感器的步态生物特征识别技术成为研究热点[1-3].步态作为生物特征之一，具有普遍性、可采集性和唯一性，且不易伪造及仿冒，可在无需主动配合的情况下，随时随地保护便携式电子产品的信息安全[4].使用加速度传感器采集人体步态信号时噪声污染难以避免，因此，从混有噪声的步态信号中提取有效信息成为研究工作重点.

在步态识别预处理过程中，信号的去噪方法主要包括：FIR低通滤波、移动均值滤波、加权移动均值滤波及小波去噪等[5-6].由于小波分析具备良好的时域局部性和多分辨率分析能力，借助小波分析与重构技术，小波去噪已经在步态识别预处理中得到了广泛应用[7].但是采集信号特征的未知性直接导致小波去噪质量的复杂性，很难正确选取去噪所需的最优参数.小波去噪原理是基于非统计理论，其特点源于小波分析技术不考虑系统的概率分布，允许系统的概率分布是未知的或非典型的.为此，本文将系统分析现有小波去噪方法在步态识别预处理中的质量效果，通过完善小波去噪最优参数选择标准来提高步态识别预处理的有效性.

1 步态加速度信号分析

1.1 步态信号的特点

加速度传感器采集人体正常行走时三维方向的加速度信号.研究显示，正常活动中人体躯干所产生加速度值在6g以下，范围集中在[-2g，2g][8].一般情况，重力方向的加速度信号幅度为-0.3g～0.8g，身体侧向腰部加速度幅度为-0.3g～0.4g.行走时，人体活动产生低频信号，频率在20 Hz以下，主要集中在1～5 Hz范围内.

1.2 信号噪声的特点

加速度传感器采集人体步态信号时，易受多种噪声源影响，包括身体晃动、环境噪声、呼吸状况、工频和高频干扰等.这些产生的噪声混杂在采集信号中，直接导致有效步态分析、特征提取的困难，主要表现为步态信号含有非正常的高频成分.加速度传感器步态采集装置虽然通过硬件滤波能去除部分噪声，但高频信号依然存在，本文以小波去噪软件滤波的方法来去除噪声影响.

2 小波去噪质量评价方法

2.1 小波去噪基本原理

小波变换实现信号去噪原理：使用小波基函数去逼近元函数，从而完成对元函数的分解.即利用小波变换的带通功能，将原信号分解为互不重叠频率的信号，再择优选取阈值来有效地去除信号中混入的噪声，小波去噪的基本步骤可概括如下：

1) 择优选择小波基函数及分解层数，计算各层小波分解系数；

2) 通过对高频系数门限阈值量化处理来消除高频部分的噪声；

3) 对低频系数和去噪后的高频系数进行小波重构，得到去噪的真实信号.

2.2 小波去噪质量评价

传统小波去噪质量评价使用的4个指标为：均方根误差(RMSE)、信噪比(SNR)、互相关系数(R)以及平滑度(r)[9]，具体公式和特点如下.

1) 均方根误差表示为

(1)

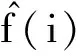
2) 信噪比表示为

(2)

式中，psiganl、pnoise为原始信号的功率和噪声功率.信噪比是指去噪前后信号间功率的比值，其值越大表示去噪效果越好.

3) 互相关系数表示为

(3)

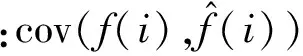
4) 平滑度表示为

(4)

平滑度是指去噪前后信号一阶差分之间方差根的比值，其值越小表示去噪效果越好.

传统评价指标虽然拥有具体物理意义，但也具有一定局限性.当去噪效果甚微或未达到去噪目的时，将出现均方根误差值接近0，相关系数接近1，而信噪比值极大的情况，显然这种评价结果是无效的.本文利用文献[10]所提出的复合评价指标来衡量步态信号小波去噪效果.

复合评价指标公式为

T=WPRMSEPRMSE+WPrPr

(5)

(6)

(7)

式中：PRMSE为标准化的均方根误差(RMSE)；Pr为标准化的平滑度；σPRMSE为PRMSE的标准差；μPRMSE为PRMSE的均值；σPr为Pr的标准差；μPr为Pr的均值.复合评价指标由均方根误差、平滑度及其变异系数定权决定，具有保留细节信息和逼近信息的物理意义.当复合评价指标值取最小值时，其对应分解层数为最优分解层数，其采用的小波基函数可作为最优小波基函数来备选.

3 步态信号小波去噪

对步态信号进行分析时，发现信号包含大量尖峰或突变等噪声，导致产生极值点、步态周期划分和特征提取不一致现象.采用小波变换的方法去噪，能有效去除噪声，最大限度地提取有用步态信息.在利用小波变换方法进行去噪的过程中，小波基函数和分解层数的选择十分重要.小波基函数和分解层数的差异直接影响真实信号特征提取的差异，Daubechies系列小波基是典型的正交小波基，具有良好的正则性，使得信号重构过程比较光滑.

小波由一组多尺度滤波器迭代而成，小波去噪对消除非平稳信号的噪声具有无可比拟的优点.文献[7]首次将小波去噪方法应用到步态加速度信号滤波中，以消除因外界环境或身体晃动等引起的噪声；文献[11]使用小波基函数db13对垂直方向加速度信号进行6层尺度小波分解和重构；文献[12]使用小波基函数db8对加速度信号进行2层尺度小波分解和重构；文献[13]使用小波基函数db5对加速度信号进行3层尺度小波分解和重构.以上3个文献都提出了各自使用的小波基函数和分解尺度层数，但未给出实际的理论依据，仅仅对比2种小波基函数分解和重构后的滤波效果，并不能解释其为最优小波基函数和最优分解层次的根本原因.

4 实验设计与分析

4.1 实验数据

实验数据来源于第一个公开的步态加速度数据集(ZJU-GaitAcc数据集[14])，包括身体5个位置(右手腕、左上臂、髋部、左大腿和右脚踝)的步态加速度数据，所使用的加速度传感器为ADXL330三轴加速度传感器，采样率为100Hz.数据集中包含3个子集，每个子集数据采集于5个身体位置6次自然行走20m、水平地面的正常行走步态信号.本文研究仅针对子集1中右髋部位置22名测试者的6次采样步态加速度数据进行实验，其加速度信号如图1所示.

图1 右髋部位置步态加速度信号Fig.1 Gait acceleration signals in position of right pelvis

4.2 实验设计

步态加速度信号小波去噪质量的复合评价指标实验设计如下：

1) 确定备选参数，分解层数为2～7层，小波基函数为db5～db13小波，阈值选定为heursure阈值准则及软阈值处理函数；

2) 计算均方根误差及平滑度的值，并归一化，计算WPRMSE与WPr权重系数的值；

3) 计算复合评价指标，当其取最小值时，所对应的小波基函数和分解层数为最优备选参数；

4) 分析备选参数小波重构后的滤波效果.

4.3 实验结果分析

1) 1名测试者1次采集步态信号的9个小波基函数与6个分解层数复合评价指标如表1所示.

表1 多层次多小波基函数的评价指标Tab.1 Evaluation index of multi-level wavelet basis function

由表1可知，无论采用何种小波基函数对步态信号进行分解，当分解层为4层时，得到的复合评价指标值都为最小值，复合指标值小于0.2；当分解层为2层时，得到的复合评价指标值都为最大值，复合指标值大于0.6.复合指标值从2层到3层间递减幅度较大，3～4层递减幅度趋于平稳，4层时为最小值，4～5层递增幅度较大，5～7层时增加幅度趋于平稳，其中3～7层的复合指标值基本处于[0.1，0.3]范围内.从数值大小分析，db8、db11、db12为复合评价指标极小的三种小波基函数，可以作为最优备选参数.

实际上，人正常步行时的步频包含在0.625～20 Hz频带内，其中1～5 Hz频率范围内集中了最多正常行走的频率信息.研究表明，99%以上的运动能量集中在15 Hz以下的信号成分中，正常行走的步频在1～3 Hz(慢速为1～2 Hz，常速为2～2.5 Hz，快速为2.5～3 Hz)[15].图2为4层分解中滤波效果对比和频谱对比图.从图2可知，以db5小波基函数对步态信号进行4层分解和重构的去噪后，在5～20 Hz频率范围内，依然含有频率信息；以db8小波基函数对步态信号进行4层分解和重构的去噪后，步态信号主要步频信息集中在1～5 Hz频率范围内，满足对步态信号研究的滤波需求.图3为db8滤波效果对比和频谱对比图，从图3可知，使用相同小波基函数db8对步态信号进行去噪，分解层数为3时，在5～10 Hz频率范围内含有较多频率信息，对应滤波后的步态信号仍然含有毛刺.

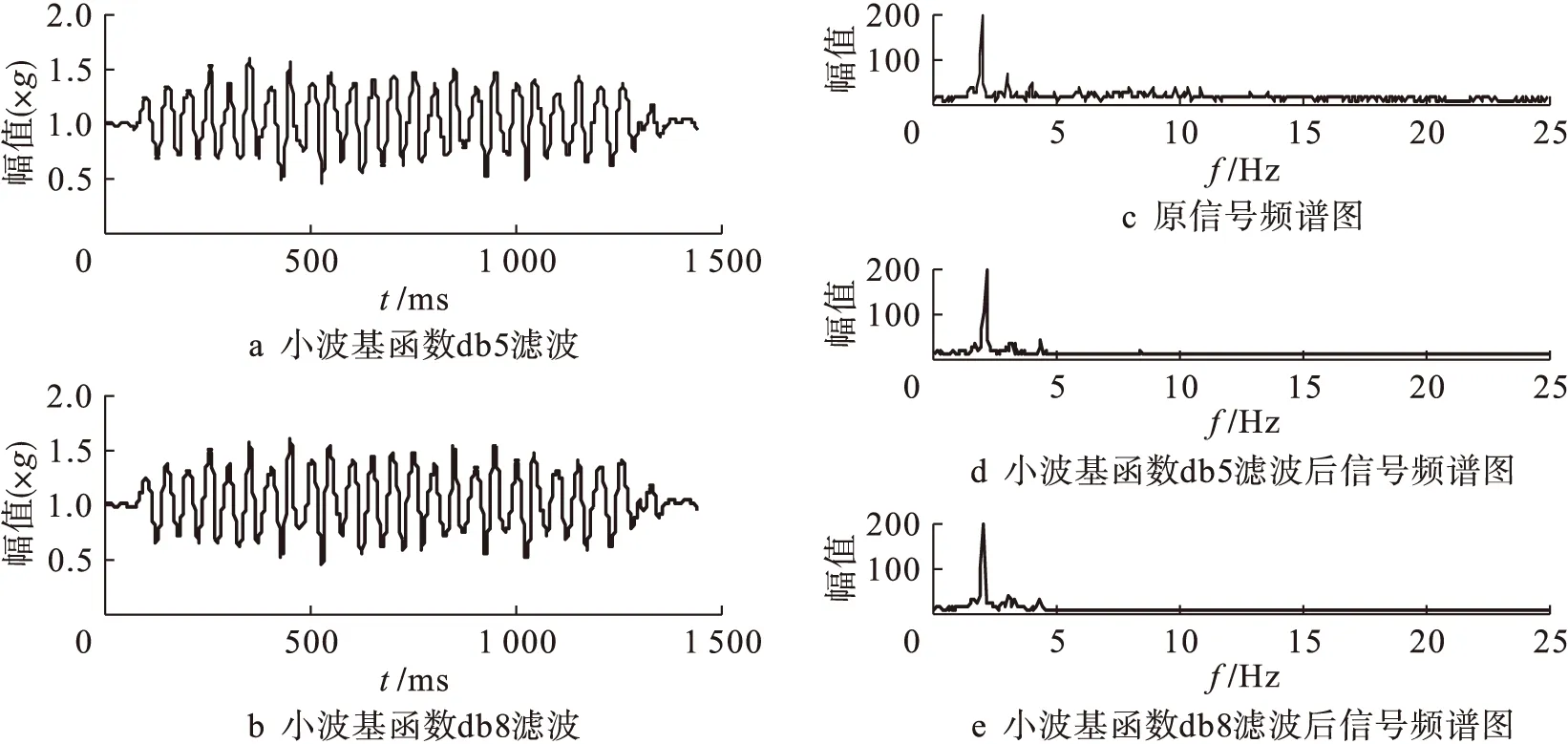
图2 4层分解中滤波效果对比和频谱对比Fig.2 Comparison in filtering effect and frequency spectrum for 4-level decomposition

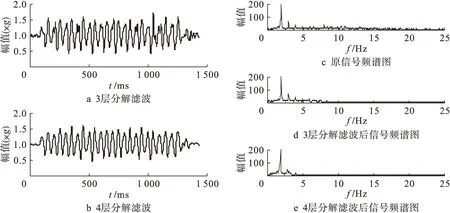
图3 db8滤波效果对比和频谱对比Fig.3 Comparison in filtering effect and frequency spectrum for db8

2) 1名测试者6次采集步态信号的9种小波基函数与6个分解层数复合评价指标图如图4所示.由图4可见，对同1名测试者进行6次采样，每一次采样用9种小波基函数进行6个层数分解和重构，所计算的复合评价指标规律与上述分析结果一致.当分解层为4层时，得到的复合评价指标值都为最小值，且其值小于0.2.最优小波基函数选取方法如表2所示.

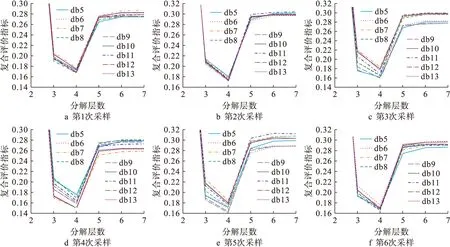
图4 复合评价趋势图(1人)Fig.4 Trend graphs of composite evaluation (1 person)

表2 最优小波基函数选取Tab.2 Selection method for optimal wavelet basis function

对比6次评价结果可知，其最小值所对应的小波基函数无规律可寻，6次评价结果具有明显不同，可见每次评价结果只适于每一次采样数据.

3) 多名测试者多次采集步态信号的多小波基函数、多分解层数复合评价指标分析.对22名测试者的6次步态信号进行132×9次复合评价指标分析，评价结果与上述研究基本一致.其中，5～7层层数分解时，10号、15号、17号测试者有部分或者全部复合指标值处于[0.3，0.4]范围内；以3层层数分解时，10号测试者有部分复合指标值大于0.3.图5为10名测试者采用不同基波函数的复合评价指标趋势图.

5 结 论

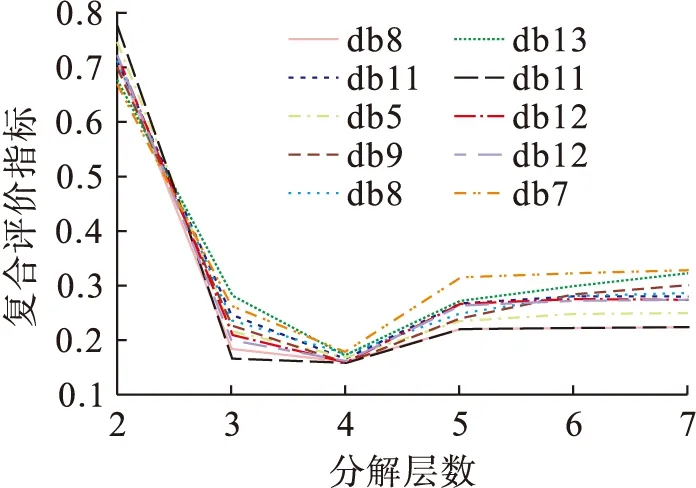
图5 复合评价趋势图(10人)Fig.5 Trend graphs of composite evaluation (10 persons)

本文将小波去噪质量评价指标应用到步态信号预处理过程中，通过评价指标值来指导小波去噪最优备选参数的选取.采用质量评价指标对步态加速度信号进行分析，得到了满意的效果，给出如下结论：

1) 以db5～db13小波基函数进行2层尺度小波分解和小波重构的质量评价指标值最大，根据判定规则，不适合用于步态信号小波去噪处理；

2) 分解层数为4层时，复合评价指标达到最小值，根据判定规则，是最适合的小波分解与重构层数；

3) 同1名测试者多次采样的步态信号进行4层小波分解和小波重构的小波基函数并不唯一.

[1]Khandelwal S，Wickström N.Gait event detection in real-world environment for long-term applications：incorporating domain knowledge into time-frequency analysis [J].IEEE Transactions on Neural System and Rehabilitation Engineering，2016，99：1-10.

[2]Derlatka M.Biometric system for person recognition using gait [C]//Foundations of Intelligent Systems.Warsaw，Poland，2011：565-574.

[3]Yang C C，Hsu Y L，Shih K S，et al.Real-time gait cycle parameter recognition using a wearable accele-rometry system [J].Sensors，2011，11(8)：7314-7326.

[4]Ren Y，Chen Y，Chuah M C.User verification leveraging gait recognition for smartphone enabled mobile healthcare systems [J].IEEE Transactions on Mobile Computing，2015，14(9)：1961-1974.

[5]Soaz C，Diepold K.Step detection and parameterization for gait assessment using a single waist-worn accelerometer [J].IEEE Transactions on Biomedical Engineering，2015，63(5)：933-942.

[6]Tran K H，Chew M T.Kalman filtering for wearable fitness monitoring [C]//Proceedings of 2015 IEEE International on Instrumentation and Measurement Technology Conference (I2MTC).Ho Chi Minh City，Vietnam，2015：2020-2025.

[7]Liu R，Duan Z，Zhou J Z，et al.Identification of individual walking patterns using gait acceleration [C]//Proceedings of lst International Conference on Bioinformatics and Biomedical Engineering.Wuhan，China，2007：543-546.

[8]谷丽华，崔畅，高松巍，等.基于MPU-6050的步态信号采集系统 [J].沈阳工业大学学报，2015，37(2)：176-182.

(GU Li-hua，CUI Chang，GAO Song-wei，et al.Gait signal acquisition system based on MPU-6050 [J].Journal of Shenyang University of Technology，2015，37(2)：176-182.)

[9]陶珂，朱建军.小波去噪质量评价方法的对比研究 [J].大地测量与地球动力学，2012，32(2)：128-133.

(TAO Ke，ZHU Jian-jun.A comparative study on validity assessment of wavelet de-noising [J].Journal of Geodesy and Geodynamics，2012，32(2)：128-133.)

[10]朱建军，章浙涛，匡翠林，等.一种可靠的小波去噪质量评价指标 [J].武汉大学学报(信息科学版)，2015，40(5)：688-694.

(ZHU Jian-jun，ZHANG Zhe-tao，KUANG Cui-lin，et al.A reliable evaluation indicator of wavelet de-noising [J].Journal of Wuhan University(Geomatics and Information Science)，2015，40(5)：688-694.)

[11]Li Y X，Wang X B，Qiao F.Gait authentication based on acceleration signals of ankle [J].Chinese Journal of Electronics，2011，20(3)：447-451.

[12]侯向锋，刘蓉，周兆丰.加速度传感器MMA7260在步态特征提取中的应用 [J].传感技术学报，2007，20(3)：507-511.

(HOU Xiang-feng，LIU Rong，ZHOU Zhao-feng.App-lication of accelerometer MMA7260 in the gait feature extraction [J].Chinese Journal of Sensors and Actuators，2007，20(3)：507-511.)

[13]翟文婷.利用加速度传感器实现人体步态识别 [D].沈阳：沈阳工业大学，2013.

(ZHAI Wen-ting.Using acceleration sensor to realize human gait recognition [D].Shenyang：Shenyang University of Technology，2013.)

[14]Zhang Y T，Pan G，Jia K，et al.Accelerometer-based gait recognition by sparse representation of signature points with clusters [J].IEEE Transactions on Cybernetics，2015，45(9)：1864-1875.

[15]Trung N T，Makihara Y，Nagahara H，et al.Performance evaluation of gait recognition using the largest inertial sensor-based gait database [C]//Proceeding of 5th IAPR International Conference on IEEE Biometrics Compendium.Osaka，Japan，2012：360-366.

(责任编辑：景 勇 英文审校：尹淑英)

Quality evaluation method for wavelet de-noising in gait recognition

TU Bin-bin1, 2, GU Li-hua1, XU Hui1

(1. School of Information Science & Engineering, Shenyang University of Technology, Shenyang 110870, China; 2. School of Information Engineering, Shenyang University, Shenyang 110044, China)

In order to overcome the difficulties in gait analysis, cycle division and feature extraction for gait acceleration singals due to the fact that the acquired signals contain a large number of higher frequency noises such as peaks or mutation, a new method, where the quality evaluation for the wavelet de-noising was adopted to select the optimal parameters for the wavelet de-noising of acceleration signals, was proposed. According to the geometric and physical meanings of quality evaluation indexes, the paramenter selection for both decomposition and reconsitution levels of optimal wavelet in the wavelet de-noising were guided by the evaluation index value. When the evaluation index took the minimum value, the correspongding decomposition level was optimal, and the used wavelet basis funtion was also optimal. The results show that the proposed method can provid the theoretical basis for the selection of both optimal wavelet basis funtion and decomposition levels for the wavelet de-noising of gait signals in the field of gait recognition.

gait; gait recognition; acceleration singal; wavelet de-noising; quality evaluation; wavelet basis function; decomposition and reconstruction; optimal parameter

2016-03-14.

国家自然科学基金资助项目(61372154).

涂斌斌(1980-)，女，辽宁沈阳人，讲师，博士生，主要从事模式识别、信号处理等方面的研究.

16∶10在中国知网优先数字出版.

http：∥www.cnki.net/kcms/detail/21.1189.T.20160907.1610.056.html

10.7688/j.issn.1000-1646.2017.01.12

TP 212

A

1000-1646(2017)01-0061-06