立体库作业均衡及货位优化仿生算法研究

杜永华，项 前，吕志军，陈 东

（1.东华大学 机械工程学院，上海 201620；2.上海精星物流设备有限公司，上海 201611）

立体库作业均衡及货位优化仿生算法研究

杜永华1，项 前1，吕志军1，陈 东2

（1.东华大学 机械工程学院，上海 201620；2.上海精星物流设备有限公司，上海 201611）

在批量订单的情况下，为了提高自动化立体仓库（AS/RS）的整体作业效率，提出了以堆垛

货位优化；作业均衡；作业效率；二进制粒子群算法；遗传算法

0 引言

自动化立体仓库（AS/RS）由于具有空间利用率较高、入出库能力较大、管理较智能化等优点，己成为现代企业生产管理中不可缺少的组成部分[2]。货位分配是影响立体仓库工作效率高低、拣选成本高低的一大主要因素，因此为了提高自动化立体库的性能，对仓储货位优化的研究越来越引起人们的重视。研究主要从两方面展开，一方面从分配策略或货位分区方面进行研究，文献[3]给出一种基于BOM（Bill of Material）分类的货位优化方法；文献[4]通过对产品频度和偏离度的研究，来实现出入库货位的优化；文献[4～6]则运用分区的策略来实现货位优化。另一方面建立货位优化数学模型，主要通过仿生算法来对模型进行优化求解，文献[6,7]分别运用贪婪算法、非支配遗传算法，以存储能耗、货架稳定性、运行效率为目标对立体仓库货位分配进行优化；文献[8]以存耗低、运行时间短为目标，运用离散粒子群算法来实现立体库货位优化。可以看出，上述货位优化研究大多集中在策略研究或者以路径、能耗及时间为目标的优化，但是在进行批量出入库操作时，由于各巷道作业的不均衡容易造成一些堆垛机闲置或超负荷运作，从而导致拣选效率和拣选质量的下降、资源的闲置，这显然不能满足批量作业的实际情况。另外，以上仿生算法的运用主要表现为遗传算法（Genetic Algorithm，GA）与粒子群算法（Particle Swarm Optimization），对二进制粒子群算法（Binary Particle Swarm Optimization，BPSO）的运用较少。据此，在批量订单操作中，本文提出了以堆垛机作业均衡以及工作效率高为目标的优化模型，与标准遗传算法比较，设计了一种基于二进制粒子群的模型求解仿生算法。

1 问题描述与数学模型

1.1 问题描述

所研究的货位优化问题可描述如下：在一个K排R层C列的储存区（其简易图如图1所示）进行批量出库或者入库操作，每张订单中的货物需要通过所处巷道堆垛机来实现出入库，当堆垛机执行完最后一个任务后返回到出入库台[9]。其中，每个巷道的堆垛机同时工作，堆垛机的工作效率通过其运行路径来衡量，每个巷道堆垛机的作业均衡也由该巷道堆垛机的运行路径来衡量。

图1 储存区简易图

1.2 数学模型

任意一个货位b均可用一个六元组（kb,rb,cb,Mb,Qb,Sb）表示，其中：（kb,rb,cb）表示货位b的坐标即（排，层，列），Mb表示货位b上所存货物的品项号，Qb表示货位b上所存货物的数量，Sb表示货位b的状态（有四种状态：任务完成、任务失败、任务正在执行、任务悬挂，默认的状态是任务完成）。

每次任务T可用如下向量表示：

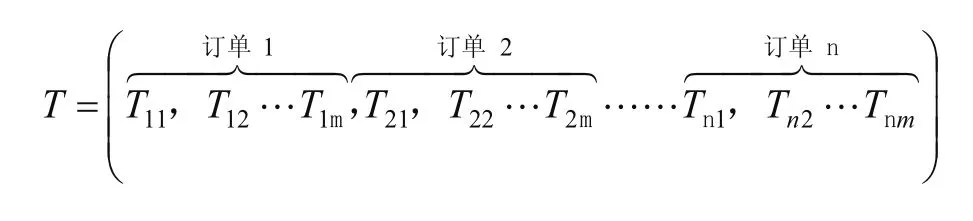
其中每张订单中的一个品项表示一个任务Ti，j=（Md, Qd），Md表示所需货物的品项号，Qd表示所需货物的数量。

为了让问题的复杂度降低，同时结合实际情况，做出如下模型假设：1）每次任务向量T都是单纯的出库或者入库；2）仓库里货物的品项和数量能够充分满足订单需求，且一个货位只能满足一个任务；3）堆垛机操作每个品项所用时间相等，且每趟只对一个目标储位进行操作；4）每个储位只能存放一个货物单元（托盘或集装箱）[11]，并且在作业之前对每个货位的状态（任务执行完成、任务失败、任务正在执行、任务悬挂，默认每个货位状态都是任务执行完成）、储位上品项信息（品项、数量、规格等）已知。

以堆垛机作业行程均衡和运行效率为目标建立优化模型，具体如下：

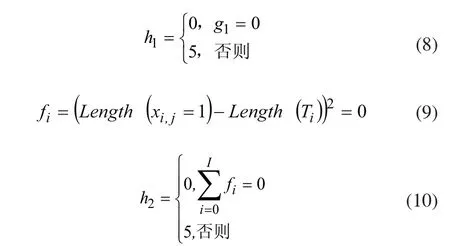
式中：i为巷道号，i = 1，2，…，I；Ni为巷道i中目标货位的集合；N为仓库中可行货位（根据任务所需的品项并且货位的状态是任务完成来确定）的集合；K为仓库中货架总的排数；R为仓库中每排货架总的层数；C为仓库中每排货架总的列数；j为粒子位索引号，j = 1，2，…，J；Length（xj=1）表示粒子中粒子位为1的个数；Length（T）为任务向量中任务的的个数；Length（xi,j=1）表示粒子中粒子位所对应的货位号位于巷道i且该粒子位为1的个数；Length（Ti）为每个任务中的货物品项号位于巷道i的任务个数S为各巷道工作行程的平均值；D为各个巷道工作行程的最大值；P为惩罚函数。

模型以最小化巷道工作行程（即最高的效率）以及各个巷道堆垛机工作量均衡为目标。约束(7)表示最后拣选的货位数与任务数相等；约束(9)表示具体到每一个巷道的任务数和该巷道拣选的货位数相等；惩罚系数(8)、(10)运用静态惩罚函数的方法来处理约束(7)、(9)[13]，对于约束(7)、(9)将其违反程度分为2个等级，不同等级采用不同惩罚系数。

2 基于二进制粒子群算法的模型求解

因为动态货位优化是一个离散型优化问题，所以适用于Kennedy和Eberhart提出的二进制粒子群算法（BPSO）[12]。基于BPSO的货位编码、解码及算法求解过程描述如下：

1）货位编号

给每个货位采取实数编号，从1开始，则每个货位的编号可以表示为：

式(11)中C和R表示的是每排货架总的列数、层数，（k，c，r）为当前货位的位置坐标。

2）粒子解码

图2 解码实例

BPSO中粒子位只有0和1两种，所以先根据任务向量中品项编号、每个货位的状态来确定可行域，让可行域的长度和粒子维度相等。粒子上相应的粒子索引号与可行域相应的货位索引是一一对应的，当该粒子位上是1时就表示相对应的货位被选中，反之就表示该货位没被选中。

则最后所选择的货位为15、20、77、89。

基于二进制粒子群的模型基本求解过程如下：

begin

确定可行货位N（根据任务所需的品项并且货位的状态是任务完成）；

参数值（主要有：种群规模（M）、粒子维度、学习因子c1、c2值、最大迭代代数等）的初始化；

t←0；

将每个可行货位采用二进制编码，初始化粒子群P（t）中每个粒子的位置、速度和个体极值；

while（not termination condition）do

for j←1 to M do

将每个粒子（xj）解码（具体见解码过程）成货位信息（Nj）；

计算目标函数值F(Nj)、F(pbestNj)、F(gbestNj)；

将货位信息（Nj）、当前最好解的货位信息（pbestNj）以及近邻中最好解的货位信息（gbestNj）分别编码（解码的逆过程）成粒子信息（xj）、当前最好的解粒子信息（pbestj）和近邻中最好解粒子信息（gbestj）

其中，N为可行货位的集合；Nj为可行货位中被选中的货位；t表示迭代次数；P(t)表示第t次迭代时的粒子群；pbestNj为j粒子当前发现的最好解货位；gbestNj为j粒子的近邻当前所发现的最好解货位；pbestj为j粒子当前所发现最好的解粒子；gbestj为j粒子的近邻当前所发现的最好解粒子；Vj为粒子群中第j个粒子的速度；函数F( )表示计算粒子的目标函数值；rand( )为属于（0，1）内的一个随机数； S（v）是sigmoid函数具体的表达式为：

3 试验及分析

为了验证优化模型的有效性，研究设计了基于BPSO和GA的模型求解仿生算法，以VS为编程环境，进行了多品项出库作业，最后对两种算法的优化结果做了对比和分析。试验对象为6排6层8列货架组成的单库型区域，有三条拣货巷道。因为进行批量出库或批量入库的时候其可行域的确定、优化模型基本都一致，所以试验中的任务向量设定为出库任务T，具体如下所示：

3.1 参数的确定

通过在不同种群规模下目标函数值的对比试验，来选取种群规模数，当种群规模小于100时，其目标函数值有明显减小的趋势，当种群规模大于100时又有上升，而种群规模等于100的时候目标函数值最小，所以种群规模选择100。具体的变化如图3所示，其中所用到的任务向量为出库任务向量T，并且每次的学习因子相同。

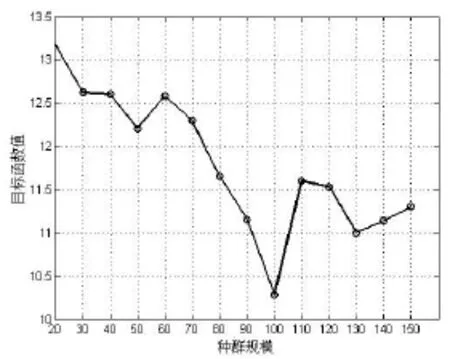
图3 不同种群规模目标函数值的对比（每种规模试验10次）

试验中用到的遗传算法（GA）是标准的遗传算法，具体的算法参数设置详情如表1所示。

表1 试验案例算法参数设置

3.2 不同优化方法的试验结果对比

试验中任务向量为出库任务向量T，图4、图5分别表示的是经过BPSO、GA优化后，目标函数值的迭代情况，它们优化结果对比如表2所示。

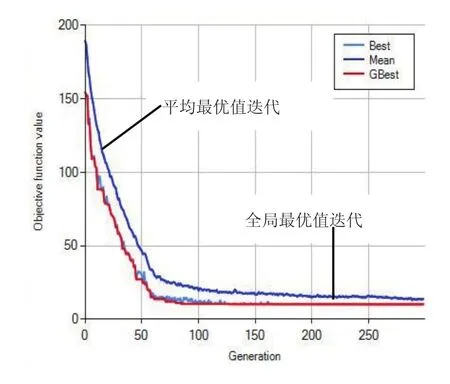
图4 基于BPSO的目标函数值迭代情况

图5 基于GA的目标函数值迭代情况

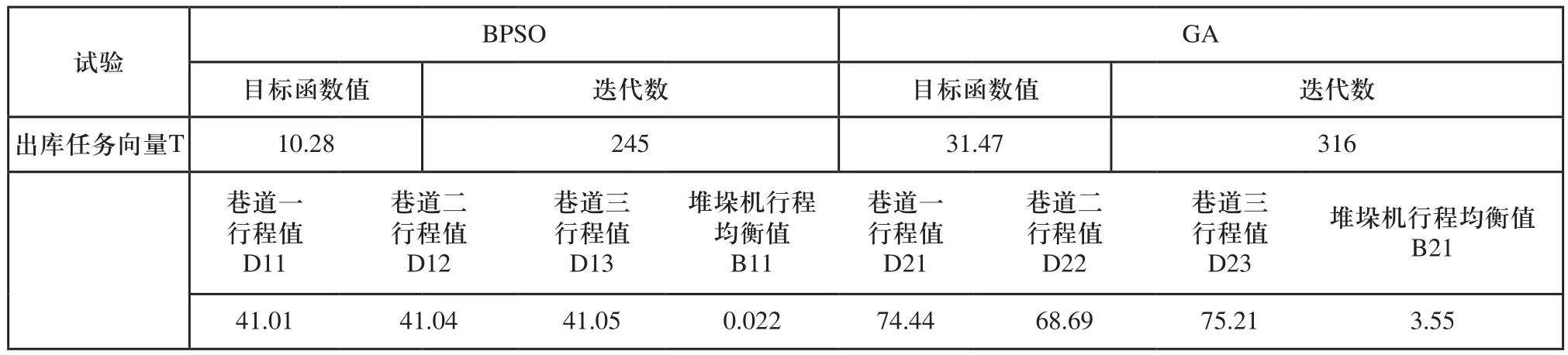
表2 BPSO与GA的优化结果对比

在立体库中每个巷道的堆垛机是并行作业的，所以每次任务所用时间取决于行程值最大的那个巷道，因此可以通过巷道的行程来表示作业效率。由图4、图5以及表2可以看出基于二进制粒子群和标准遗传的仿生算法对模型的求解都能取得较好的结果，BPSO经过245代后可得到目标函数值10.28、堆垛机行程均衡值B11为0.022及行程值D13为41.05，GA经过316代后可得到目标函数值31.47、堆垛机行程均衡值B12为3.55及行程值D23为75.21，显然BPSO比GA具有如下四点优势：1）可以以较少的代数得到较好的目标函数值；2）每代的种群差异较大，全局搜索能力更强；3）因为B11远小于B12，各堆垛机作业更加均衡；4）工作效率η提高了45.42%。通过以上分析，基于二进制粒子群算法求解的模型较符合实际的批量订单操作，提高了仓储作业的整体效率和质量。

4 结束语

在进行批量出入库时，为了提高仓储整体作业效率，提出了基于二进制粒子群的堆垛机作业均衡及货位优化模型，并且与标准遗传算法进行了优化效果对比，通过试验验证了模型及算法的有效性。由于本文只局限于单纯出库或入库作业研究，后续研究将针对出入库混合作业各巷道均衡性进一步展开。所研究的基于二进制粒子群的作业均衡以及货位优化模型及仿生算法已经在企业仓储管理系统中得到了应用，并取得了良好地成效。

参考文献：

[1] 丁立言,张铎.仓储自动化[M].1版.北京:清华大学出版社,2002,14-28.

[2] Hsieh S,Tsai K C. A BOM oriented class-based storage assignment in an automated storage/retrieval system[J]. International Journal of Advanced Manufacturing Techology,2001,17(9):683-691.

[3] 穆聪聪,郭敏.基于产品频度与偏离度的货位分配策略研究[J].物流科技,2015,06:107-112.

[4] T. A. Ajol, Ismail I, S. S. Gran, et al. An enhanced storage location assignment policy by minimizing handling cost for warehouse XYZ[A].International Conference on Computer, Communications, and Control Technology[C].IEEE,2015.

[5] Park B C, Foley R D, Frazelle E H. Performance of miniload systems with two-class storage[J].European Journal of Operational Research,2006,170(1):144-155.

[6] 张思建,方彦军,贺瑶,肖勇.基于模拟退火算法的AVS/RS多批货箱入库货位优化[J].武汉大学学报(工学版),2016,02:315-320.

[7] 李珍萍,于洋涛,李文玉.基于贪婪算法的仓库货位优化问题研究[J].物流技术,2015,05:242-244.

[8] 印美,洪荣晶,刘林.基于非支配遗传算法的自动化仓库动态货位优化[J].组合机床与自动化加工技术,2015,03:31-34+37.

[9] Li H P, Fang Z F, Ji S Y. Research on the Slotting Optimization of Automated Stereoscopic Warehouse Based on Discrete Particle Swarm Optimization[A].IEEE the, International Conference on Industrial Engineering and Engineering Management[C].2010:1404-1407.

[10] 李晓,项前,吕志军,管树林.基于单双亲混合GA的复杂拣选作业优化[J].计算机工程与设计,2015,12:3359-3364.

[11] 张小川.现代仓储物流技术与装备[M].北京:化学工业出版社,2013:37-38.

[12] 邓雪,李家铭,曾浩健,陈俊羊,赵俊峰.层次分析法权重计算方法分析及其应用研究[J].数学的实践与认识,2012,07:93-100.

[13] 黄竞伟,朱福喜,康立山.计算智能[M].1版.北京:科学出版社,2010,6.

[14] Kennedy J,Eberhart R. A.discrete binary version of the particle swarm algorithm[A].Proceeding of the World Multiconference on Systemics,Cybernetics and Informatics[C].New Jersy:Piscatawary,1997,4104-4109.

Bionic algorithm research on AS/RS operation balance and location assignment optimization

DU Yong-hua1，XIANG Qian1，LYU Zhi-jun1，CHEN Dong2

TP18

：A

1009-0134(2017)01-0122-05

2016-09-11

上海市自然科学基金资助项目（15ZR1400600）；2015松江区产学研创新项目计划

杜永华（1992 -），男，湖南邵阳人，硕士研究生，研究方向为智能制造。

机作业均衡与高仓储效率为目标的立体库货位优化模型。设计了基于二进制粒子群（Binary Particle Swarm Optimization，BPSO）和遗传算法（Genetic Algorithm，GA）的模型求解仿生算法。通过同一个立体库批量订单作业实例，验证了所提模型及算法的有效性，算法试验及分析表明，基于BPSO的立体库作业均衡及货位优化效果较遗传算法显著。