基于极大似然估计的鲁棒信息滤波算法研究
2017-02-10薛博阳胡柏青常路宾高敬东
薛博阳 胡柏青 常路宾 高敬东
(海军工程大学导航工程系 武汉 430033)
基于极大似然估计的鲁棒信息滤波算法研究
薛博阳 胡柏青 常路宾 高敬东
(海军工程大学导航工程系 武汉 430033)
为了有效提高传统卡尔曼滤波算法的鲁棒性,论文从滤波算法的极大似然估计的本质分析了传统滤波算法不具鲁棒性的原因,提出了基于广义极大似然估计的一般性鲁棒方法。同时,为了实现对粗大野值的剔除,将鲁棒滤波算法扩展到信息滤波领域,推导了一般性的鲁棒信息滤波框架。仿真实验验证了论文所研究算法的有效性。
卡尔曼滤波; 信息滤波; 鲁棒; 野值; 极大似然估计
Class Number TP301.6
1 引言
以卡尔曼滤波为代表的状态空间最优估计方法在卫星姿态估计、目标跟踪、组合导航等领域得到了广泛的研究和应用。卡尔曼滤波是一种基于贝叶斯最优估计和统计线性回归框架,通过线性组合的方式利用先验信息和观测信息来确定状态最优后验信息的方法[1]。要获得贝叶斯估计的最优解需要用无穷多个参数去描述输出的概率分布,这在实际中是无法做到的,同时贝叶斯最优估计算法中所涉及多维积分,对于非线性和(或)非高斯的情况,该积分一般没有解析解,只能采用近似方法。针对非线性问题,我们可以采用积分近似的非线性滤波算法,如今年来广泛研究应用的无味卡尔曼滤波算法、求容积卡尔曼滤波算法(CKF)等。这些算法在一般性的非线性问题中都得到了很好的应用效果[1~2]。
事实上,目前很多非线性滤波算法仍然采用了卡尔曼的线性递归框架,在线性递归框架中先验信息和观测信息通过线性组合,得到最优的后验信息[3]。此处的最优是指最小均方误差意义下的最优,最小均方误差也是一种l2范数最小的准则。然而统计学的研究表明l2范数最小估计不具有鲁棒性[4]。即当假设条件和现实参数不相符时,哪怕发生了微小的偏移,估计量都会发生明显的变化,而当实际参数和假设具有较大差别时甚至会造成滤波发散。因此研究鲁棒滤波算法以提高其在实际系统中的适应性是滤波算法研究领域的另一个重要研究方面[5]。近年来,相关学者基于广义极大似然估计提出了一系列鲁棒滤波算法,这些算法的核心都是通过引入新的鲁棒代价函数来替代原有的基于l2范数的代价函数[6]。这其中应用最为广泛的是Huber提出的两段代价函数,这种代价函数在误差较小时等效为l2范数,而当误差较大时则对误差进行截断平均。然而,很容易理解,当误差很大时,单纯的截断平均并不能很好的处理较大野值误差,在这种情况下,应当直接剔除相应的野值[7]。针对这种问题,我们虽然可以设计相应的鲁棒代价函数来实现对粗大野值的剔除,然而,鲁棒代价函数在滤波框架中是通过对残差进行加权来实现的,而该加权过程中存在一个矩阵求逆的过程。因此,如果直接将具有野值剔除功能的代价函数直接代入滤波框架中,则很容易引起数值不稳定性问题,从而造成滤波中断[8~10]。
信息滤波是其对应卡尔曼滤波的等价形式,在信息滤波框架中,滤波过程是通过对相应方差阵和权值阵进行求逆来实现的[4]。因此,前文中提到的因矩阵求逆而引起的数值不稳定性问题可以在信息滤波框架中得到自然的避免[5]。基于上述背景,本文研究了一种基于信息滤波的鲁棒滤波算法,实现了在一般鲁棒化的过程中对粗大野值的剔除,从而有效提高了滤波算法精度。
2 基于极大似然估计准则的卡尔曼滤波
考虑如下线性统计状态空间模型
xk=Fk-1xk-1+qk-1
yk=Hkxk+rk
(1)
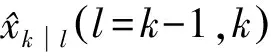
(2)
(3)
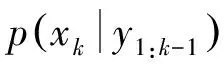
(4)
(5)
(6)
则
(7)
从式(4)和式(7)可以看出,卡尔曼滤波是基于l2范数最小准则下的最优解。然而l2范数对非高斯噪声及粗大误差特别敏感,不具有鲁棒性。
3 基于广义极大似然估计的鲁棒卡尔曼滤波

(8)
式(8)中最小化的问题可以通过对代价函数求导并置零得到,即
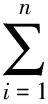
(9)
其中φ=ρ′一般被称之为影响函数。定义如下两个矩阵
(10)
(11)
则式(9)可以写成如下矩阵形式

(12)
将式(5)和式(6)代入式(12)可得
(13)
定义如下两个矩阵
(14)
(15)
将式(14)和式(15)代入式(12)可得
(16)
式(16)正是如下最小化问题的解
(17)
对比式(17)和式(7)可以看出鲁棒卡尔曼滤波和传统卡尔曼滤波具有相同的结构形式,区别仅仅在于状态预测方差和量测噪声方差的不同。因此可以将此思想应用到鲁棒卡尔曼滤波中,即构造代价函数对卡尔曼滤波中的状态预测方差和量测噪声方差进行修正,并将修正后的量代入卡尔曼滤波框架。
不同的代价函数会产生不同的鲁棒效果。Huber提出一种代价函数

(18)
这种代价函数综合了l1和l2范数的性质,具有较好的鲁棒性。当γ→∞时,这种广义极大似然估计退化为l2范数最小的最小二乘估计,而当γ→0时,则退化为l1范数最小的中值估计。这种代价函数在鲁棒卡尔曼滤波中得到了广泛的应用,并扩展到了非线性滤波领域。该鲁棒代价函数对应的加权函数(即式(10)和式(11)中权矩阵的元素)为
(19)
从权重函数中可以看到这种代价函数对于较大的误差值即野点只是进行了截断平均而并未剔除,因此会对滤波结果造成不利影响。针对含有较多及较大野点的情况,我们可以考虑如下形式的权重函数
(20)
这种权重函数对于较大的野点直接进行剔除,从而不会对滤波结果造成影响。
但是从式(14)和式(15)中可以看出,权重函数在对方差阵进行加权过程中有一个求逆的过程,由于式(20)中的权重函数中有一项为零,因此不能直接应用于卡尔曼滤波框架。针对该问题,本文提出在信息滤波框架下进行鲁邦化的思想。
4 基于广义极大似然估计的鲁棒信息滤波
信息滤波是其对应卡尔曼滤波的等价形式,区别在于在滤波递推的过程中传递的是方差的逆。首先定义I=P-1,下面给出信息滤波的具体形式:
时间更新
(21)
(22)
量测更新
(23)
(24)
从式(23)和式(24)中可以看到,在信息滤波过程中只是用到了量测方差阵的逆,因此在其对应的鲁棒化算法中也是只需要修正后的量测方差阵的逆。基于这种认识,来构造基于权函数式(20)的修正量测方差阵的逆。
根据式(15)可得
(25)
其中
(26)
将修正后的量测方差阵的逆代入式(23)和式(24)中即可得到鲁棒化的信息滤波算法。从该算法构造过程中可以看到,其中不涉及对零元素进行求逆的过程,因此不存在数值问题。
5 仿真实例
为了验证本文所提算法的有效性,考虑单变量非平稳增长模型(Univariate Nonstationary Growth Model, UNGM),该模型经常被用来作为验证滤波算法的基准模型。UNGM模型的离散时间动态系统方程如下:
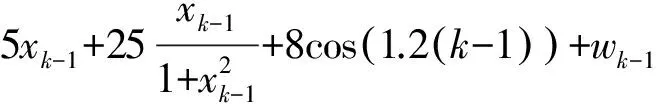


由于该模型为非线性,因此需要采用非线性滤波算法,本文采用UKF算法。由于鲁棒化算法从线性到非线性函数的过渡已有成熟的研究成果而且比较直接,因此此处不做详细介绍。本文提出的鲁棒信息滤波算法也很容易扩展到非线性滤波框架中。此处比较三种滤波算法:传统UKF,基于式(19)的鲁棒UKF(RUKF),以及基于式(20)和本文提出的鲁棒信息滤波框架的鲁棒信息UKF(RUIF)。
观测噪声服从如下形式的干扰高斯分布
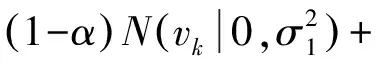
(28)
其中,α被称之为干扰因子,在该仿真实验中设为0.3。λ是干扰高斯分布方差相对于主高斯分布方差的比重。实验中,首先令σ1=1,λ依次设置为1~20之间的整数,并通过以下指标比较滤波算法的性能:
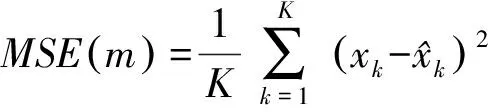
(29)
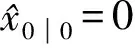
三种滤波算法在50次Monte Carlo仿真下的MSE如图1所示,MSE对应的均值和方差如图2所示。从图中可以明显看出,传统的卡尔曼滤波算法不具有鲁棒性,在观测量中含有干扰噪声时,对应的滤波精度会严重降阶。在传统滤波框架中引入鲁棒代价函数可以对干扰噪声进行有效地抑制,对应的滤波精度也明显提高,但是由于传统鲁棒化过程中对较大的野点没有进行剔除处理,会损失一部分滤波精度,如图1中14,20,30,47处的滤波结果。而本文提出的方法一方面继承了鲁棒滤波算法的优势,同时实现了对野点的有效剔除,因此滤波精度最好。
6 结语
本文从广义极大似然估计的角度研究了鲁棒卡尔曼滤波算法,该鲁棒滤波框架需要对加权矩阵进行求逆运算,因此对于能够剔除粗大野值的代价函数并不适用。针对该问题,本文提出了鲁棒信息滤波算法,在保证一般鲁棒卡尔曼滤波算法所具有的鲁棒性同时,实现了对粗大野值的在线剔除。实验结果证明了该算法的有效性。
[1] Kalman R. A New Approach to Linear Filtering and Prediction Problems[J]. Journal of Basic Engineering,1960,82(1):35-46.
[2] 付梦印,邓志红,闫莉萍.Kalman滤波理论极其在导航系统中的应用[M].第二版.北京:科学出版社,2010.
[3] Crassidis J L, Junkins J L. Optimal Estimation of Dynamic Systems[M]. Boca Raton, FL: Chapman & Hall/CRC,2012.
[4] Chang L B, Hu B Q, Li A, et al. Transformed unscented Kalman filter[J]. IEEE Transactions on Automatic Control,2013,49(2):1400-1402.
[5] Chang L B,Hu B Q,Chang G B,et al.Huber-based novel robust unscented Kalman filter[J]. IET Science,Measurement & Technology,2012,6(6):502-509.
[6] Chang L B,Hu B Q,Chang G B,et al.Robust derivative-free Kalman filter based on Huber’s M-estimation methodology[J]. Journal of Process Control,2013,23(10):1555-1561.
[7] Chang L B,Hu B Q,Chang G B,et al.Multiple Outliers Suppression Derivative-Free Filter Based on Unscented Transformation[J]. Journal of guidance,control,and dynamics,2012, 35(6):1902-1907.
[8] 吴枫,谷丛,朱启举.SINS辅助GPS检测技术在弹载组合导航中的应用[J].弹箭与制导学报,2014,34(5):17-25.
[9] 李杨,胡柏青,覃方君,等.MEMS陀螺的抗野值自适应滤波降噪方法[J].压电与声光,2015,37(4):590-594.
[10] 李京书,许江宁,覃方君,等.非线性EKF对准方法进行正逆向分析的应用[J].弹箭与制导学报,2014,34(3):1-6.
Algorithm Design of Robust Information Filtering Based on Generalized Maximum Likelihood Estimation
XUE Boyang HU Baiqing CHANG Lubin GAO Jingdong
(Navigation Engineering Department, Naval University of Engineering, Wuhan 430033)
In order to robustly the traditional Kalman filters, the Kalman filters are analyzed based on the perspective of maximum likelihood and the reason of its sensitivity to the disturbance has been pointed out. Furthermore, a robust Kalman filtering algorithm is developed based on the generalized maximum likelihood. Meanwhile, in order to eliminate thick outliers, the robust algorithm is extended to the information filtering and the general roust information filter has been derived. Simulation results have demonstrated the superiority of the proposed method over the traditional methods.
Kalman filter, information filter, robust, outlier, maximum likelihood estimation
2016年7月10日,
2016年8月27日
国家自然科学基金资助项目(编号:61304241,61374206)资助。
薛博阳,男,硕士,研究方向:惯性技术及其应用。胡柏青,男,博士,教授,研究方向:惯性技术及其应用。常路宾,男,博士,讲师,研究方向:惯性技术及其应用。高敬东,男,博士,教授,研究方向:惯性技术及其应用。
TP301.6
10.3969/j.issn.1672-9730.2017.01.009
