一种改进CB模型的彩色图像混合噪声去除方法*

周 千 李文胜

(西安航空学院理学院 西安 710077)



一种改进CB模型的彩色图像混合噪声去除方法*

周 千 李文胜

(西安航空学院理学院 西安 710077)

将分数阶偏微分理论和CB模型相结合应用于彩色图像混合噪声去除。对于添加混合噪声的彩色图像,首先,利用MCM模型去除图像中的椒盐噪声,然后将处理后的彩色图像分解为色度C和亮度B两部分,用分数阶偏微分模型处理亮度B,而对于色度C,由于其受到单位长度的限制,在处理时非常困难,因此,在角度域中平滑色度C,这样可以避免计算时的困难,并能够提高平滑的效率,然后将处理后的亮度B和色度C合成为新的彩色图像。最后通过实验证明了该方法的有效性。

彩色图像去噪; 分数阶偏微分方程; CB模型; 角度域

Class Number TP391

1 引言

在图像获取和传输的过程中,会产生大量的噪声,这些噪声会对图像的质量产生严重的影响。基于偏微分方程的图像去噪方法不但能较好地抑制噪声,而且能保持图像的边缘纹理特征,较好地克服了保持图像特征和抑制噪声这一对矛盾。针对不同的噪声,各种去噪方法应运而生。然而,现有的去噪方法大多是针对某一特定噪声的,在混合噪声情形下效果不理想。鉴于此,美籍韩国学者Seongjai Kim提出了一种混合PM模型[1]、TV模型[2]和MCM模型的αβϖ(ABO)模型[3],利用MCM模型能够有效地去除椒盐噪声,而PM模型、TV模型则能够去除高斯噪声,因此,该模型能够有效地平滑混合了高斯噪声和椒盐噪声的图像。然而,无论是PM模型还是TV模型,都是基于整数阶偏微分对图像进行去噪处理。而分数阶微分作为整数阶微分的一种推广,已经在数学、医学等许多研究领域得到了广泛的应用[4～10]。利用分数阶微分进行图像去噪,可以大幅提升图像的高频成分、增强图像的中频成分、非线性保留图像的低频成分,因此可以较好地保留图像平滑区域中灰度变化不大的纹理细节信息,同时,还可以避免二阶非线性扩散所特有的“阶梯效应”[11]。

在图像处理的研究进程中,一般的图像去噪模型都是针对灰度图像进行处理[12～13]。然而,在实际生活中,人们接触到的图像主要是彩色图像,因此,对彩色图像进行去噪处理具有非常重要的现实意义[14～19]。传统的彩色图像处理方法都是采用RGB空间,分别对彩色图像的红、绿、蓝三分量进行处理,最后再将处理后的三个分量合成彩色图像。虽然这种方法具有实现过程简单、处理速度快等特点,但由于彩色图像的三个分量原本是一个有机的整体,相互之间具有很高的相关性,将RGB三个分量分开处理往往会导致最终得到的彩色图像失真,降低去噪后彩色图像的质量。

受上述文献的启发,为了能够有效去除彩色图像中的高斯噪声和椒盐噪声,同时能够更好地保持图像的边缘纹理特征等细节信息,将分数阶偏微分理论和CB(Chromaticity-Brightness)模型相结合应用于彩色图像的混合噪声去噪。首先,将一幅彩色图像I分为色度C(Chromaticity)和亮度B(Brightness)两部分,其中,

这里,‖·‖表示L2范数。亮度B表示RGB彩色向量的长度,色度C用来存储单位长度上的彩色信息。对于亮度B,大多数的研究者采用TV模型(全变分图像去噪模型)进行处理,但TV模型属于二阶偏微分方程的范畴,去噪结果会出现阶梯效应,本文采用分数阶偏微分方程对亮度B进行处理;对于色度C,由于其受到单位长度的限制,在处理时非常困难,本文将在角度域中处理色度C,不仅可以降低计算的难度,还可以提高去噪的效率[16],然后将处理后的亮度B和色度C合成新的彩色图像。最后通过实验证明了该方法的有效性。

2 αβϖ(ABO)模型

为了能够有效地去除高斯噪声和椒盐噪声,Seongjai Kim提出了一种混合PM模型、TV模型和MCM模型的αβϖ(ABO)模型[3],如下:

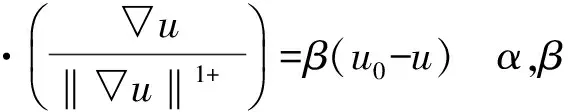
(1)

其中,|▽u|和‖▽u‖在数学上的定义是一样的,都是梯度模。之所以写成不同的符号,是因为Seongjai Kim对|▽u|和‖|▽u‖给出了不同的差分格式。在模型(1)中,当α=ϖ=0时,模型退化为TV模型,而当α=1,β=ϖ=0时,则退化为MCM模型,当α=0,ϖ>0时,则成为PM模型。特别地,当α=1+ϖ,ϖ>0,β>0时,称为强化的TV模型。

3 基于分数阶偏微分方程和CB模型的混合去噪模型

3.1 基于分数阶偏微分方程的混合去噪模型

为了能够有效去除高斯噪声和椒盐噪声,同时能够更好地保持图像的边缘纹理特征等细节信息,受到αβϖ(ABO)模型的启发,提出如下的去噪模型:

α,β,ϖ≥0,1≤ε≤2

(2)

类似于文献[20]中的方法,当离散该模型时,采用自适应时间步长并忽略时间t的迭代。因此,在式(2)中,令ut=0,则式(2)可改写为

(3)

因此,可以通过离散方程(3)来代替方程(2),这样可以大大减少计算的复杂程度。

3.2 彩色图像的CB模型

在RGB空间,一幅彩色图像可以看作一个映射:

(4)

大多数的图像去噪方法是建立在RGB空间体系上,CB模型也是来源于RGB颜色空间,它把I分为色度C和亮度B两部分,其中,

这里,‖·‖表示L2范数。亮度B表示RGB彩色向量的长度,色度C用来存储单位长度上的彩色信息。

对于亮度B,采用基于分数阶偏微分方程的图像去噪模型(2)进行处理,分数阶微分可以大幅提升图像的高频成分、增强图像的中频成分、非线性保留图像的低频成分,因此可以较好地保留图像平滑区域中灰度变化不大的纹理细节信息,同时,还可以避免二阶非线性扩散所特有的“阶梯效应”。

而对于色度C的去噪,将在角度域中进行。首先令V=B(x)C(x)=(u,v,w),并且令

(5)

由于u,v,w≥0,因此0≤φ,θ≤π/2。考虑如下的最小值问题:

(6)

式(6)对应的在角度域中的Euler-Lagrange方程是:

φt= ▽ε·((R(φ,θ))p-2▽εφ)

+sinφcosθ(R(φ,θ))p-2|▽εθ|2

(7)

θt=▽ε·(cos2φ(R(φ,θ))p-2▽εθ)

(8)

其中R(φ,θ)=(‖▽εφ‖2+cos2φ‖▽εθ‖2)1/2。

在式(6)～(8)中,令p=1,则可得基于向量的ABO模型:

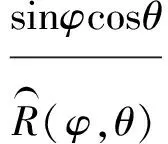
(9)

(10)

本文算法实现主要包括以下三个步骤:

1) 先用MCM模型去除混合噪声中的椒盐噪声;

2) 把去除椒盐噪声后的彩色图像分解为色度C和亮度B两部分。对于亮度B,将其代入式(3)中进行处理,而对于色度C则利用式(5)(9)(10)进行迭代求解;

3) 最后,将处理后的色度C和亮度B合成新的彩色图像。

4 模型的数值实现

为提高方程的去噪能力并同时保护图像的细节,对|▽u|的离散常常采用一些特殊的方法。Seongjai Kim提出了ENoD(Essentially non-dissipative)的差分格式来离散MCM模型中的扩散因子|▽u|,这可以有效地消除椒盐噪声并保护图像的边缘纹理特征[3]。ENoD差分格式定义如下:

给定一个网格点P(i,j),设(k,l)是P(i,j)的8-邻域中的点之一。令

(11)

对上述8个差分值按从小到大进行排序:

(12)

则在P(i,j)点计算|▽u|的ENoD差分格式为

(13)

ENoD差分格式综合了两个最小的差分值去逼近梯度值,因此,它不是数学意义上的梯度模的精确值,即当网格的空间步长趋于零时,它不一定趋于该点的梯度模,但是,从数值实验结果来看,它能有效地保护图像的边缘纹理细节等信息。

(14)

为了计算的方便,选取分数阶微分定义的前三项作为分数阶微分的近似:

(15)

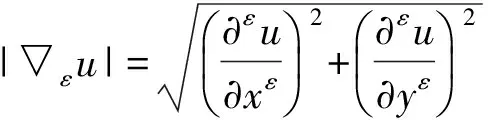
5 实验结果与分析

为了验证本文模型的有效性,在Matlab7.0的平台下进行了两组比较实验。实验结果主要通过计算去噪后图像的峰值信噪比(PSNR)作为去噪性能的客观评价标准。

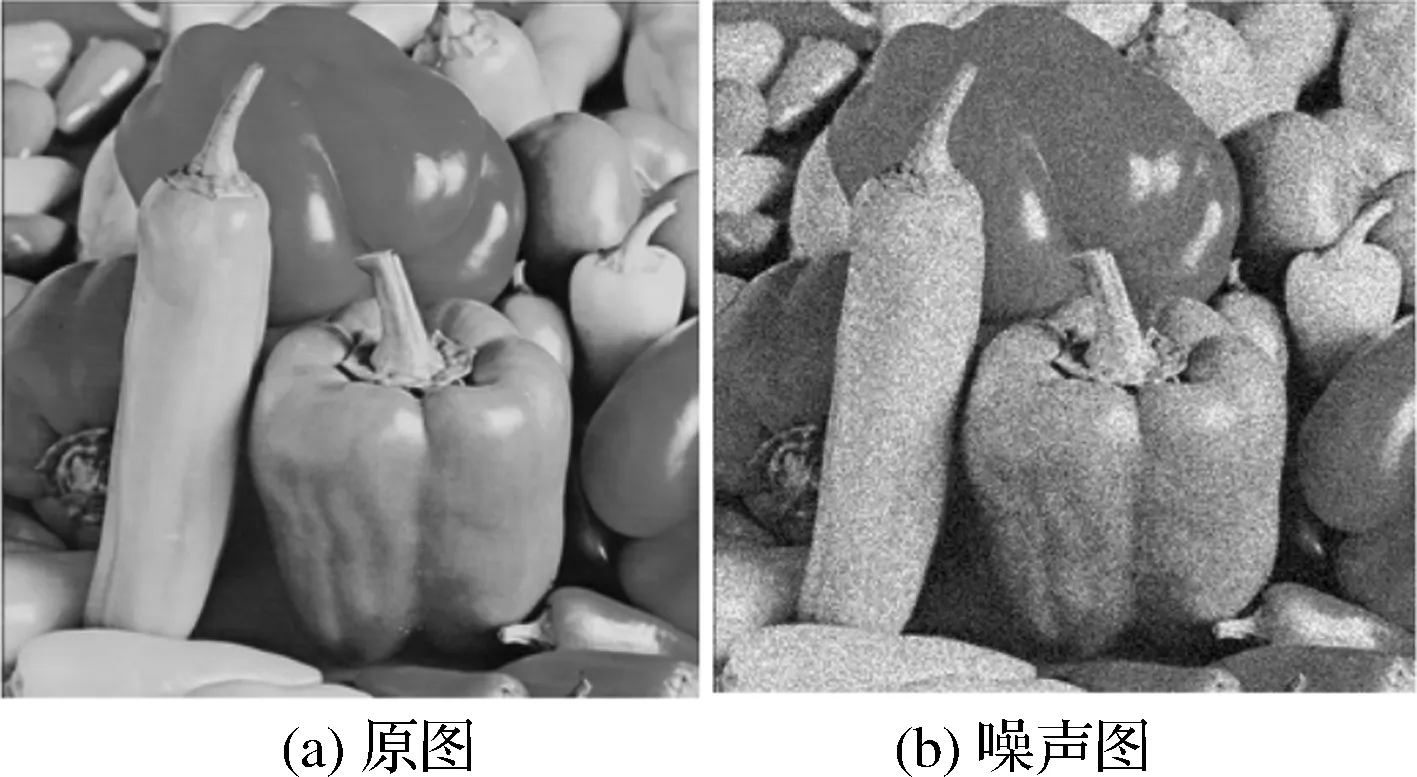
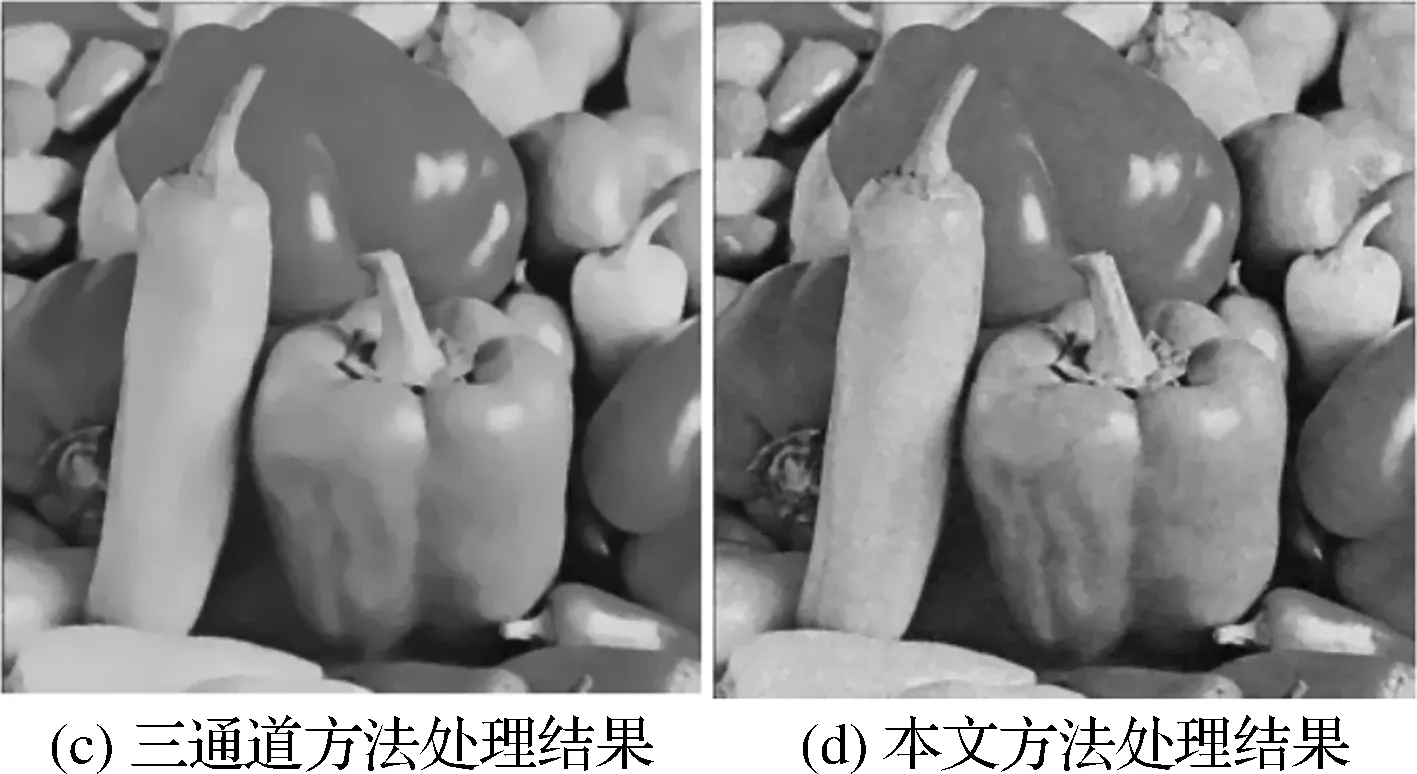
图1 Pepper图像及三通道方法和 本文方法的去噪效果图

第一组实验是将本文方法与传统的基于RGB三通道的图像去噪算法进行比较,实验结果如图1所示。选取标准的Pepper图像进行实验,图1(a)是原图,图1(b)是添加均值为0,方差为0.01的高斯噪声图,PSNR=17.3460。图1(c)是基于RGB三通道的图像去噪算法处理的结果,从图中可以看出,该方法处理后的彩色图像有明显的失真现象,特别是在图中红色辣椒的部分,从而降低了去噪后彩色图像的质量,其原因是彩色图像RGB三个分量原本是一个有机的整体,相互之间具有很高的相关性,将RGB三个分量分开处理势必会导致图像失真。图1(d)是本文方法处理的结果,选取参数α=0.001,β=0.01,ϖ=0.02,ε=0.6,从图中可以看出,经过本文方法处理后的图像更加接近于原图,视觉效果较好。最后,从实验结果也可以看出,在噪声强度相同的条件下,本文模型处理后得到的图像的PSNR=26.8637高于基于RGB三通道的图像去噪算法处理后得到的图像的PSNR=24.8106,进而从客观角度说明了本文模型的有效性和优越性。

第二组实验是将本文方法与αβϖ(ABO)模型进行比较,实验结果如图2所示。选取标准的Lena图像进行实验,图1(a)是添加均值为0,方差为0.01的高斯噪声,以及密度为0.02的椒盐噪声图,PSNR=23.9587。图1(b)是基于ENoD差分格式的MCM模型去除椒盐噪声后的图像,可以看出,MCM模型能够较好的去除椒盐噪声,并能够保护图像的边缘和细节。对于剩下的高斯噪声,则分别采用αβϖ(ABO)模型与本文方法进行平滑,结果如图2(c)和(d)所示,在αβϖ(ABO)模型中,选取参数α=0,β=0.04,ϖ=0.02,去噪后图像的PSNR=31.1365,本文方法中,选取参数α=0.001,β=0.01,ϖ=0.02,ε=0.6,去噪后图像的PSNR=33.8023,无论是视觉方面,还是客观的数据比较,本文方法都要优于αβϖ(ABO)模型。

图2 Lena图像及αβϖ(ABO)模型和 本文方法的去噪效果图

6 结语

本文将分数阶偏微分理论和CB模型相结合应用于图像去噪,提出了一种基于分数阶偏微分方程和CB模型的彩色图像混合噪声去除方法。首先,利用基于ENoD差分格式的MCM模型去除混合噪声中的椒盐噪声,然后将处理后的彩色图像分解为色度C和亮度B两部分。

利用E-αβϖ(ABO)模型处理亮度B,而将色度C的处理转化到角度域中进行,最后将处理后的亮度B和色度C合成为新的彩色图像。实验结果表明,本文提出的方法既能有效的加强图像的纹理信息,并能获得更好地视觉效果。

[1] Perona P, Malik J. Scale-space and edge detection using anisot ropic diffusion[J]. IEEE Trans on Pattern Analysis and Machine Intelligence,1990,12(7):629-639.

[2] Rudin L, Osher S, Faatemi E. Nonlinear total variation based noise removal algorithms[J]. Physica D,1992,60(4):259-268.

[3] Seongjai Kim. PDE-based image restoration: a hybrid model and color image denoising[J]. IEEE Transaction on Image Processing,2006,15(5):1163-1170.

[4] Jian Bai, Xiang-chu Feng. Fractional-Order anisotropic diffusion for image denoising[J]. IEEE Trans. Image Process,2007,16(10):2492-2502.

[5] 张富平,周尚波,赵灿.基于分数阶偏微分方程的彩色图像去噪新方法[J].计算机应用研究,2013,30(3):946-949. ZHANG Fuping, ZHOU Shangbo, ZHAO Can. Novel color image denoising method based on fractional-order partial differential equation[J]. Application Research of Computers,2013,30(3):946-949.

[6] 蒋伟.基于分数阶偏微分方程的图像去噪新模型[J].计算机应用,2011,31(3):753-756. JIANG Wei. New image denoising model based on fractional-order partial differential equation[J]. Journal of Computer Applications,2011,31(3):753-756.

[7] 黄果,许黎,陈庆利,等.基于空间分数阶偏微分方程的图像去噪模型研究[J].四川大学学报(工程科学版),2012,44(2):91-98. HUANG Guo, XU Li, CHEN Qingli, et al. Research on image de-noising based on space fractional partial differential equations[J]. Journal of Sichuan University(Engineering Science Edition),2012,44(2):91-98.

[8] 杨柱中,周激流,郎方年.基于分数阶微积分的噪声检测和图像去噪[J].中国图象图形学报,2014,19(10):1418-1429. YANG Zhuzhong, ZHOU Jiliu, LANG Fangnian. Noise detection and image de-noising based on fractional calculus[J]. Journal of Image and Graphics,2014,19(10):1418-1429.

[9] 高朝邦,周激流.基于四元数分数阶方向微分的图像增强[J].自动化学报,2011,37(2):150-159. GAO Chaobang, ZHOU Jiliu. Image enhancement based on quaternion fractional directional differentiation[J]. Acta Automatica Sinica,2011,37(2):150-159.

[10] 李博,谢巍.基于自适应分数阶微积分的图像去噪与增强算法[J].系统工程与电子技术,2016,38(1):185-192. LI Bo, XIE Wei. Image enhancement and denoising algorithms based on adaptive fractional differential and integal[J]. Systems Engineering and Electronics,2016,38(1):185-192.

[11] You Y L, Xu W, Tannenbanm A, et al. Behavioral analysis of anisotropic diffusion in image processing[J]. IEEE Trans on Image Processing,1996,5(11):1539-1553.

[12] Catte F, Lions P L, Morel J M, et al. Image selective smoothiung and edge detection by nonlinear diffusion[J]. SIAM J Num Anal,1992,29(1):182-193.

[13] Alvarez L, Lions P L, Morel J M. Image selective smoothiung and edge detection by nonlinear diffusion[J]. SIAM J Num Anal,1992,29(3):845-866.

[14] Chan TF, Kang SH, Shen J. Total variation denoising and enhancement of color images based on the CB and HSV color models[J]. Vis. Commun. Image R,2001,12(4):422-435.

[15] Tang B, Sapiro G, Caselles V. Color image enhancement via chromaticity diffusion[J]. IEEE Trans. Image Process,2001,10(5):701-707.

[16] Fang Li. A novel algorithm for color image denoising based on the CB color model[C]//2011 13thIEEE Joint International Computer Science and Information Technology Conference, Chongqing,2011:67-70.

[17] 杜宏伟,张翼.基于偏微分方程的彩色图像去噪综合模型[J].云南民族大学学报(自然科学版),2011,20(6):497-499. DU Hongwei, ZHANG Yi. Combined model for color image denoising based on the partial differential equation[J]. Journal of Yunnan University of Nationalities(Nature Sciences Edition),2011,20(6):497-499.

[18] 陈北京,戴慧,刘全升,等.基于四元数表示的彩色图像泊松噪声去除[J].东南大学学报(自然科学版),2013,43(4):717-723. CHEN Beijing, DAI Hui, LIU Quansheng, et al. Poisson noise removal for color images using quaternion representation[J]. Journal of Southeast University(National Science Edition),2013,43(4):717-723.

[19] 孙莉.一种基于平均曲率的彩色图像去噪分裂模型[J].兰州大学学报(自然科学版),2012,48(3):128-132. SUN Li. A splitting mean curvature-based model for color image de-noising[J]. Journal of Lanzhou University(Natural Science),2012,48(3):128-132.

[20] Tony F. Chan, Stanley Osher, Jianhong Shen. The digital TV filter and nonlinear denoising[J]. IEEE Transaction on Image Processing,2001,10(2):231-241.

A Method for Removing Mixed Noise of Color Image by Improving CB Model

ZHOU Qian LI Wensheng

(School of Science, Xi’an Aerotechnical University, Xi’an 710077)

Combing fractional-order differential theory with Chromaticity-Brightness (CB) model, in order to deal with the mixture of the salt & pepper and Gaussian noises, a novel color image denoising model is proposed. For a color image with mixed noises, the salt & pepper noise can be eliminated by the MCM model effectively. Then, the processed color image is decomposed into chromaticity component and brightness component. Secondly, fractional-order differential model is used for brightness component. The chromaticity component will be smoothed in angle domain to avoid the difficulty and to improve efficiency. Thirdly, the retorted image is got by multiplying the recovered chromaticity with recovered brightness. Finally, we proved the validity of the proposed model through the experiment.

color image denoising, fractional-order differential equation, CB color model, angle domain

2016年7月3日,

2016年8月21日

陕西省教育厅专项科研计划项目(编号:15JK1379);西安航空学院科研基金资助项目(编号:2016KY1214;2014KY1210)资助。

周千,男,硕士,讲师,研究方向:基于偏微分方程的图像处理。

TP391

10.3969/j.issn.1672-9722.2017.01.032