基于Lp范数广义变分正则化图像滤波*

王益艳

(四川文理学院物理与机电工程学院 达州 635000)



基于Lp范数广义变分正则化图像滤波*

王益艳

(四川文理学院物理与机电工程学院 达州 635000)

传统变分PDE方法,如基于L2范数调和模型,全变分TV模型和广义TV模型等。在滤除噪声的同时,不能有效地保留边缘等细节。针对该不足,提出了一种基于Lp范数(1≤p≤2)的广义变分滤波模型,采用差曲率作为自适应的调整参数,实现了图像的各向异性处理。仿真实验结果表明,该算法比传统变分PDE能更有效地检测边缘与平坦区的孤立噪声点,能有效地克服阶梯效应并保留局部细节信息,在主观视觉效果和客观评价指标两方面都更具明显优势。

图像滤波; 差曲率; 各向异性;Lp范数

Class Number TP391

1 引言

图像在获取和传输等过程中,会受到各种因素的影响,比如大气状况、成像设备与物体之间的相对运动等[1],从而引起图像失真,导致图像质量退化。因此,在对图像进行后续处理(如边缘检测、分割、识别等)[2]之前,必须先进行滤波预处理。传统的滤波方法包括均值滤波、高斯滤波等,但这两种方法虽然能在一定程度上能去噪声,但也容易导致图像细节模糊。基于变分PDE的方法是目前图像处理领域的研究热点,已被广泛应用于图像滤波、修复、分割、超分辨率重建等各领域[3]。从扩散的角度分析,基于L2范数的调和模型本质是各向同性的[4],与传统高斯滤波器的滤波效果基本等价[5]。全变分模型[6～7]只沿着边缘方向扩散,满足各向异性,能在去噪的同时较好地保护边缘细节,但该模型在平坦区域存在“阶梯”效应[8]。后来,Song等[9]提出一种基于Lp范数(1≤p≤2)的广义TV去噪复原模型,该模型可看成是前面两种模型的一种折中形式,其滤波效果容易受常数p的影响。针对该不足,文献[10]采用梯度作为边缘检测算子计算p参数,对传统方法进行改进。该方法根据图像的内部结构特征,可自适应选取p参数的值,在一定程度上提高了图像滤波效果。但由于其采用梯度作为图像的边缘检测算子,而梯度对噪声不具有鲁棒性[11]。因此,其复原效果还有进一步提升的空间。基于此,提出了一种基于Lp范数(1≤p≤2)的广义变分滤波模型,采用差曲率作为自适应的调整参数,实现了图像的各向异性处理。该算法能有效地检测边缘与平坦区的孤立噪声点,进一步克服阶梯效应并更好保留局部细节信息,仿真实验结果表明,该方法比传统变分PDE在主观视觉效果和客观评价指标两方面都更具明显优势。

2 本文方法

文献[12]提出的边缘检测算子是基于梯度|▽u|的,它不能有效地识别边缘和灰度渐变区及去除平坦区内的强噪声,基于此,本文采用基于差曲率的检测算子,其定义如下

S=||uηη|-|uξξ||

(1)

其中uηη和uξξ分别表示u在η和ξ方向上的二阶导数,表达式如下

(2)

(3)

而η为图像的梯度方向,ξ为与η垂直的切线方向,分别表示为

(4)

差曲率算子的具体性能[13]如表1所示。

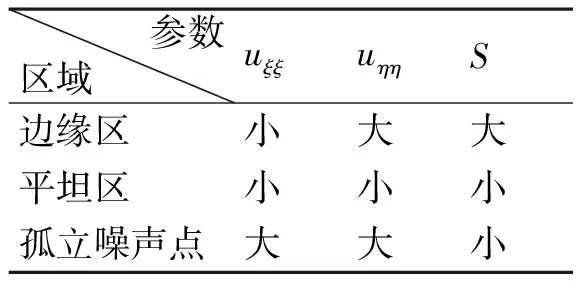
表1 差曲率算子性能

引入S算子后,新的自适应变分模型如下

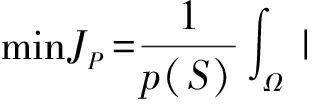
(5)

其中,上式第1项为正则项,第2项为数据保真项,λ为拉格朗日乘子。p函数的值域应该满足:在图像平坦区域,自适应选取去噪效果较好的L2范数,则p函数的值应趋于2;在图像的边界、纹理处,自适应选取较好保留局部细节的L1范数,p函数的值应趋于1。因此,根据表1中S算子在平坦区域和边缘区的取值大小关系,p函数应当为一个单调递减函数,本文选取如下表达式:

(6)

其中,Gσ表示对图像进行高斯平滑。

该模型的欧拉-拉格朗日方程为

-▽(|▽u|p(S)-2▽u)+λ(u-u0)=0

(7)

引入时间步长,其对应的梯度下降流为

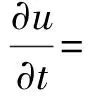
(8)

将式(8)在二维局部坐标(η,ξ)下展开为

+λ(u0-u)

(9)

引入新的变量,将式(9)改写为

(10)

其中,

(11)

上式中α和β分别为切线方向梯度方向的扩散系数。在图像边缘处,S值较大,p(S)趋于1,此时β趋于0,图像仅沿切线方向扩散,扩散项趋于TV模型,可较好地保持边缘;在图像平坦区及灰度渐变区,S值较小,p(S)趋于2,此时α≈β,图像具有各向同等扩散性能,扩散项趋于调和模型可消除阶梯效应。

与传统复原模型相比,该模型切线方向的扩散系数总是为正,因此能更好地识别平坦区和灰度渐变区。同时,此方法从图像结构来说是局部自适应的,克服了整幅图像都采用同一扩散模型的缺点。

采用半点格式的中心差分[14]来离散化式(10)中的PDE,其迭代形式可表示为

(12)

3 实验结果与分析

为论证本文方法的滤波效果,采用均方根误差(RMSE)和峰值信噪比(PSNR)进行量化评价。其表达式分别为

(13)

(14)

式中,g表示大小为C×L的原始图像,f表示滤波后的图像。RMSE值越小,PSNR值越大,图像滤波效果越好。

实验一:分别以彗星图像和liftingbody图像为测试对象,对原始图像分别加入σ=10和σ=15的噪声。将L2范数模型[4]、TV模型[7]、Song模型[9]、Zhang模型[12]和本文方法进行对比试验,滤波图像的主观视觉效果如图1和图2所示,各种模型下峰值信噪比(PSNR)和均方根误差(RMSE)如表2所示。

图1 各种模型的彗星图像滤波效果比较(σ=10)

图2 各种模型的liftingbody 图像滤波效果比较(σ=15)

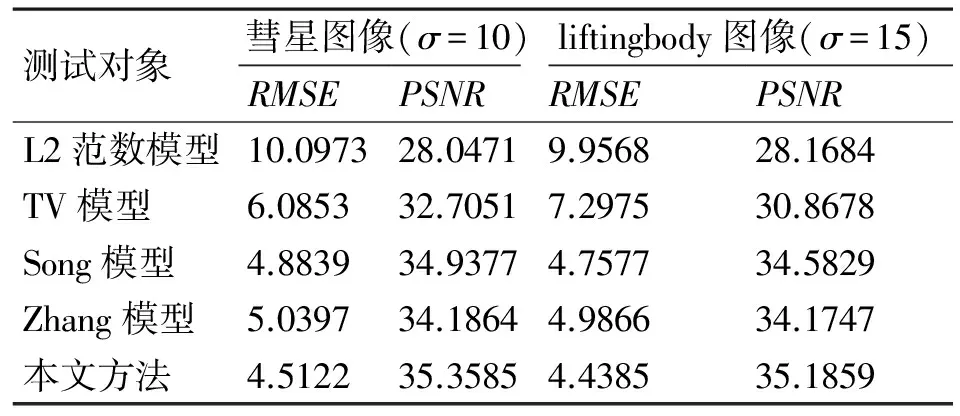
测试对象彗星图像(σ=10)liftingbody图像(σ=15)RMSEPSNRRMSEPSNRL2范数模型10．097328．04719．956828．1684TV模型6．085332．70517．297530．8678Song模型4．883934．93774．757734．5829Zhang模型5．039734．18644．986634．1747本文方法4．512235．35854．438535．1859

通过上述实验可知,L2范数模型[4]滤波后图像存在一定的模糊,TV模型[7]滤波后图像在平坦区出现了“阶梯”效应,而Song[9]、张红英[12]提出的改进模型虽然比传统模型的滤波效果有所提高,但本文方法无论是主观视觉效果,还是客观评价标准都是最佳。

4 结语

针对传统变分PDE模型存在的不足,提出了一种基于Lp范数(1≤p≤2)的广义变分滤波模型,采用差曲率作为自适应的调整参数,实现了图像的各向异性处理。该算法能有效的检测边缘与平坦区的孤立噪声点,进一步克服阶梯效应并更好保留局部细节信息,实验仿真结果表明,该方法比传统变分PDE在主观视觉效果和客观评价指标两方面都更具明显优势。关于模型参数的选取及该模型在彩色图像恢复中的应用将是今后研究的重点。

[1] Michael Felsberg. Autocorrelation-Driven Diffusion Filtering[J]. IEEE Transactions on Image Processing,2011,20(7):1797-1806.

[2] Mohammad R. H., M. Omair Ahmad., Chunyan Wang. An edge-adaptive laplacian kernel for nonlinear diffusion filters[J]. IEEE Transactions on Image Processing,2012,21(4):1561-1572.

[3] Kang-Yu Ni. Variational PDE-based image segmentation and inpainting with applications in computer graphics[D]. USA, Los Anggeles: University of California,2008.

[4] Tikhonov A N, Arsenin V Y. Solution of ill-posed problems[M]. Washington DC, Winston,1977.

[5] 冯象初,王卫卫.图像处理的变分和偏微分方程方法[M].北京:科学出版社,2009. FENG Xiangchu, WANG Weiwei. Variational and partial differential equations method for image processing[M]. Beijing: Science Press,2009.

[6] L. I. Rudin, S. Osher, E. Fatemi. Nonlinear total variation based noise removal algorithms[J]. Physica D,1992,(60):259-268.

[7] Chan T F, Osher S, Shen J. The digital TV filter and nonlinear denoising[J]. IEEE Transaction on Image Processing,2001,10(2):231-241.

[8] Guichard F, Moisan L, Morel J M. A review of PDE models in image processing and image analysis[J]. Journal de Physique Ⅳ,2002,92(12):137-154.

[9] Song B. Topics in variational PDE image segmentation, inpainting and denoising[D]. USA Los Angeles: University of California,2003.

[10] Blomgren P., Mulet P., Chan T., et al. Total variation image restoration: numerical methods and extensions[C]//Proceedings International Conference on Image Processing, Santa Barbara: IEEE Press, Oct 26-29,1997:384-387.

[11] Qiang Chen, Philippe Montesinos, Quan Sen Sun, et al. Adaptive total variation denoising based on difference curvature[J]. Image and Vision Computing,2010,28(3):298-306.

[12] 张红英,彭启琮.全变分自适应图像去噪模型[J].光电工程,2006,33(3):50-53. ZHANG Hongying, PENG Qicong. Adaptive image denoising model based on total variation[J]. Opto-Electronic Engineering,2006,33(3):50-53.

[13] 郭永彩,彭兰辉,高潮.基于局部坐标二次微分的自适应全变分去噪复原[J].光电工程,2012,39(8):10-16. GUO Yongcai, PENG Lanhui, GAO Chao. Adaptive total variation image denoising and restoration based on the quadratic differential in the local coordinate system[J]. Opto-Electronic Engineering,2012,39(8):10-16.

[14] 王益艳.基于全变分模型的新型数值实现算法[J].云南民族大学学报(自然科学版),2010(3):211-215. WANG Yiyan. A New Numerical Realization Algorithm Based on the Total Variational Model[J]. Journal of Yunnan University Nationalities(Natural Sciences Edition),2010(3):211-215.

Image Restoration Based on LpNorm Generalized Variational Regularization

WANG Yiyan

(School of Physics and Mechanical & Electronic Engineering, Sichuan University of Arts and Science, Dazhou 635000)

The traditional variational PDE methods, such as harmonic model based onL2norm, total variation(TV) model and the generalized TV model have shortcoming that can not effectively retain edge details during filtering noise. In this paper, a generalized variational filtering method is proposed based onLpnorm model, the differential of curvature is adopted as the adaptive adjustment parameters to realize image anisotropy processing. Simulation results show that the algorithm can effectively detect isolated noise point edge with the flat area, and overcome the staircase effect and preserve the local details. Meanwhile, the proposed method have more obvious advantages both subjective visual effect and objective evaluation than the traditional variational PDE methods.

image filtering, differential curvature, anisotropy,Lpnorm

2016年7月16日,

2016年8月23日

四川省教育厅自然科学一般项目(编号:16ZB0355);达州市科技计划应用基础研究项目(编号:KJJ2015001)资助。

王益艳,男,硕士,讲师,研究方向:图像处理与模式识别。

TP391

10.3969/j.issn.1672-9722.2017.01.029