基于灰关联度系数的证据组合方法*

卢彦龙 王 拓 徐 宏

(西安交通大学电子与信息工程学院 西安 710049)



基于灰关联度系数的证据组合方法*

卢彦龙 王 拓 徐 宏

(西安交通大学电子与信息工程学院 西安 710049)

分析了D-S方法及其改进方法的不足,基于灰关联度系数提出了一种新的冲突证据处理算法。首先,以灰关联系数作为衡量标准,把每条证据当做离散的点,求出证据体集合中其它证据与它的相似程度。然后把相似程度进行归一化处理得到相似度,该相似度表示的是该证据的重要程度。把该相似度当做每条证据体的权重,对证据体加权合成新的证据体模型。最后用新证据体融合得到结果。通过算例表明:该方法与其他改进方法比较,具有收敛速度快,计算方法简单,易于工程实现的优点。

D-S证据理论; 证据冲突; 灰色关联度; 信息融合

Class Number TP301.6

1 引言

Dempster-Shafer(D-S)证据理论是1967由Dempste[1]提出,又经其弟子Shafer进一步推广和发展。目前已广泛应用于地理空间系统[2]、网络安全[3]、电力自动化[4]等领域。证据理论虽然有很多优点,但Zadeh[5]在研究中发现,该理论处理高冲突证据时会产生与事实相反的结论。自此许多学者对该问题进行了深入的研究,提出了很多解决方法。总体来看,解决冲突方法分为两类。

一类是对D-S理论合成规则的修改,主张修改组合规则的学者认为D-S组合规则在解决高冲突问题时会出现有悖常理的情况,是由于D-S组合规则对冲突分配不合理而造成的,进而提出了不同的冲突分配法则,Lefevre[6]、权文[7]、刘海燕[8]等人都在这方面做了相关研究。另一类是对证据模型的修改,主张修改证据模型的学者认为D-S组合规则本身并没有问题,合成结果之所以有悖常理,造是成证据模型本身有问题,与合成规则无关,所以应该对证据模型进行修改,如Murphy[9],邓勇[10],韩德强[11]等。

对合成规则的修改难度大、容易破坏D-S组合规则的一些良好的数学性质,而且在一些应用领域,传感器容易受到干扰而失效,造成证据体数据出错,这种情况下把合成结果出现悖论的原因归结于D-S组合规则就有些许不妥。所以,本文也基于第二类改进方法提出一种新的证据体修改方法。该类方法的难点在于权重的生成确定,本文引入灰关联度系数生成权重,直接求出证据间的相似度,使合成冲突证据时,能够更加快速、准确的得出结论。

2 D-S 组合规则简介

D-S理论中,对某一个问题的所有认知的可能的解所构成的集合叫做识别框架,常用Θ表示,其中Θ中的元素两两相斥,及Θ={A1,A2,…,AN}。称Ai(1≤i≤N)为识别框架中的一个焦元,其中N为识别框架中总的元素个数。根据集合的定义可知,该集合有2N个子集,用2Θ表示。

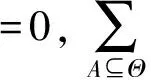
定义2:D-S证据理论是对多条证据融合处理的方法,合成规则表示为[1]

(1)

例:某一刑事案件有三个犯罪嫌疑人A,B,C,现有两个证人给出的嫌疑犯Θ={A,B,C}的基本信度赋值如下:

E1:m1(A)=0.99,m1(B)=0.01,m1(C)=0

E2:m2(A)=0,m2(B)=0.01,m2(C)=0.99

用D-S组合规则合成结果:m(A)=m(C)=0,m(B)=0.0001/(1-K)=1。

在本例中,两个证人都对B嫌疑人的支持度很低,但合成的结果却为B,这显然有悖常理。

3 基于灰关联度的改进方法

3.1 灰色关联度

灰色关联分析的基本思想是:根据序列中各点的贴近程度来度量该序列组成曲线几何形状的相似程度[12]。序列曲线的几何形状越接近,它们的关联程度就越大[12]。

定义3:若Xi(i=1,2,…,N)为观测对象序列,Xi(k)为Xi关于第k个指标的观测数据,称Xi=(xi(1),xi(2),…,xi(N))为序列Xi(k)的行为指数序列,则其他观测对象Xj=(xj(1),xj(2),…,xj(N))(i≠j)(j=1,2,…,N)与行为指数序列Xi对应的每个点的灰关联度系数定义为[12]γ(xi(k),xj(k)):

(2)

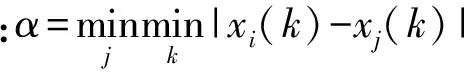
则序列Xi和序列Xj总的关联度为两条序列每个点的相似度之和,定义为Crd(Xi,Xj):

(3)

3.2 基于灰关联度的改进方法

基于灰关联度的改进方法认为若证据体与证据体集合中大多数证据之间的几何形状比较接近,则认为该证据对判断出正确结果的作用高,在证据合成时,应该赋予该证据较大的权重,而证据体之间几何形状接近程度用相似度表示,所以可以通过灰关联度直接求出证据体之间的相似度。求证据体相似度的方法如下:

若识别框架Θ中有N个元素,mi,mj(i≠j)为其中任意两个不同的基本信度赋值,则把mi,mj按以下形式映射到上面叙述的灰关联度里的Xi,Xj:

Xi(1)=mi(A1),Xi(2)=mi(A2),…,Xi(N)=mi(AN)

Xj(1)=mj(A1),Xj(2)=mj(A2),…,Xj(N)=mj(AN)

及Xi=(mi(A1),mi(A2),…,mi(AN))

Xj=(mj(A1),mj(A2),…,mj(AN))

用式(2)做一点改变,就可以求出两条证据每个点的相似度,定义为γ(mi(Ak),mj(Ak)):

(4)

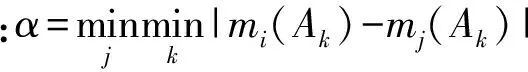
对照上述式(3),则两条证据mi,mj(i≠j)总的相似度为两条证据每个点的相似度之和,定义为Crd(mi,mj):

(5)

求出mi,mj(i≠j)相似度之后用相似度作为权重,对证据体模型进行修改,最后把修改后的证据体用D-S组合规则得到融合结果。

基于灰关联度的改进方法通过灰关联度求证据之间的相似度,通过式(4)的分母可以看出,当两条证据的BPA对识别框架Θ中每个元素的支持程度越接近,|mi(Ak)-mj(Ak)|越小,求出的两条证据每个点的相似度越大。若两条证据的BPA相差不大,也就是两条证据对识别框架中目标的支持程度冲突不大,根据式(5)可以得出两条证据的相似度越大。

两条证据间的相似度反映的证据信息的相似程度,若一条证据和证据集合中大部分证据对识别框架中元素的支持程度冲突不大,通过式(4)、式(5)可知,该类证据的相似度比较大则在合成时该证据应该赋予较高的权值。相反,若一条证据和证据集合中大部分证据的对别框架中元素的支持程度冲突较大,则|mi(Ak)-mj(Ak)|比较大,导致求出的每个点相似度较小,则证据之间的相似度也越小。

3.3 改进方法的计算流程

1) 计算出证据mi(1≤i≤N)与除自己之外证据体mj(1≤j≤N)每一个点的灰关联度系数矩阵PM:

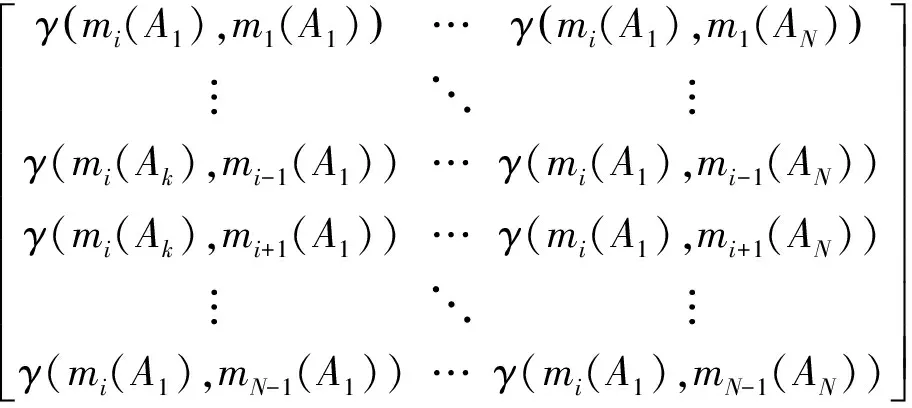
2) 对灰关联度系数矩阵PM对行求和得到mi,mj(i≠j)的相似程度Crd(mi,mj):

3) 计算出mi与其余证据体的总相似度TotalCrd(mi):

4) 把总相似度归一化的到归一化相似度

5) 把归一化相似度作为每条证据的权值

ωi=NormaCrd(mi)

6) 求出证据模型

对新证据模型进行N-1次D-S组合规则得到融合结果。

4 算例分析

下面利用邓勇文献[10]的算例,对比D-S组合规则,Murphy法,邓勇法,韩德强法分析结果,说明本文提出的方法在处理冲突证据融合方面的优越性能,计算时ρ=0.05。五种方法融合结果如表1所示。

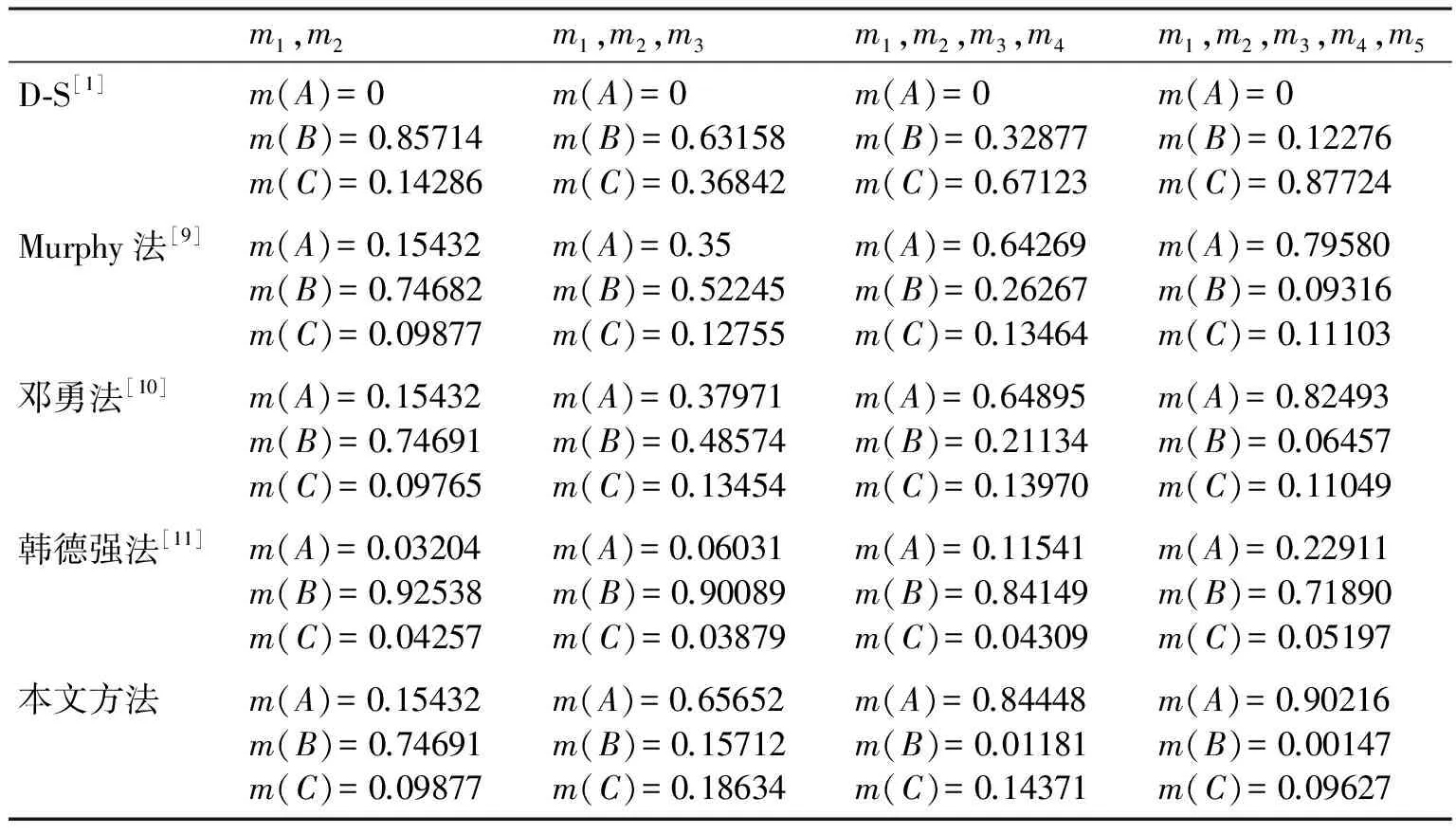
表1 五种证据组合方法的比较

本文算例中,m2为干扰证据,除它以外,其它四条证据都支持目标A。在用D-S方法融合时,由于m2(A)=0即使别的证据都支持A,依然无法识别出正确的结论,产生与事实相悖的结论,即D-S方法无法处理高冲突问题。韩德强方法虽然随着证据数目的增加对证据A的支持程度在慢慢变大,但由于干扰证据的影响,在文中五条证据合成完之后,依然无法得出正确的结论,可以看出在文中这种算例条件下,用该方法得到正确结论需要更多的证据。

Murphy法,邓勇法和文中提出的基于灰关联度的改进方法在合成时都能够比较迅速地合成结果。在合成判断时,当我们把阈值设为0.7时,可以看出用Mruphy方法和邓勇法融合识别时都能融合出正确的结论,但需要四次融合(m1,m2,m3,m4,m5)。而本文的方法只需三次(m1,m2,m3,m4)融合就可以得出正确的结论。当五条证据融合完以后,可以看出,本文对A的支持度为0.90216,远大于邓勇法的0.82493。分析其原因可以发现,Mruphy方法由于其对证据的简单平均,使得重要程度低的证据影响了合成合理结果的速度;韩德强方法用求权重时引入了负指数函数,使得第二条证据占有的权重较大,导致收敛速度严重降低;邓勇法由于Jousselme距离退化为欧氏距离,在度量两条证据之间的相似性时,不具有直接性,放大了证据之间的差异性,突出了冲突证据的权重,导致收敛速度慢。

本文算例中,五种合成方法k值变换趋势如图1所示。

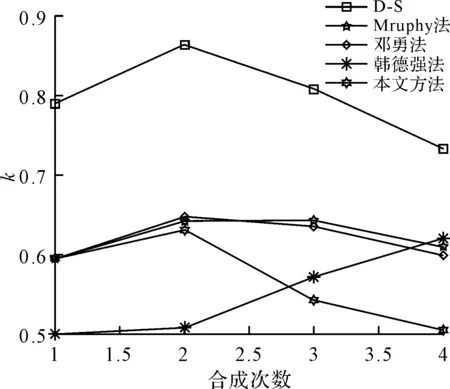
图1 五种合成方法k值比较

可以看出D-S方法融合时,k值一直居高不下,韩德强法在文中例子中,由于收敛速度较慢,致使k值在例子中的数据合成完成之前,一直在增加,没有收敛,Mruphy方法和邓勇法的k值虽然随着合成次数的增加都在减小,但减小速率慢于本文提出的方法。

5 结语

在军事应用的领域,传感器容易受到自然环境和人为因素的影响,导致少量传感器的测量结果异常,从而得到冲突证据。通过文中分析可以看出,当证据间存在严重冲突时,D-S方法无法得出正确结论,Mruphy方法和邓勇法收敛速度较慢,故而本文提出了一种基于灰关联度系数的证据组合方法。通过算例可以看出,本文提出的方法收敛速度快,鲁棒性好,计算方法简单,易于工程实现。

[1] 韩德强,杨艺,韩崇昭.DS证据理论研究进展及相关问题探讨[J].控制与决策,2014,29(1):1-8. HAN Deqiang, YANG Yi, HAN Chongzhao. Advances in DS evidence theory and related discussions[J]. Control and Decision,2014,29(1):1-8.

[2] Paul A. Elmore, Frederick E. Petry, Ronald R. Yager. Geospatial Modeling Using Dempster-Shafer Theory[J]. IEEE Transactions on Cybernetics,2016:1-11.

[3] 汤永利,李伟杰,于金霞.基于改进D-S证据理论的网络安全态势评估方法[J].南京理工大学学报,2015,39(4):406-411. TANG Yongli, LI Weijie, YU Jinxia. Network security situational assessment method based on improved D-S evidence theory[J]. Journal of Nanjing University of Science and Technology,2015,39(4):406-411.

[4] 司马莉萍,舒乃秋,李自品,等.基于SVM和D-S证据理论的电力变压器内部故障部位识别[J].电力自动化设备,2012,32(11):72-76. SIMA Liping, SHU Naiqiu, LI Zipin, et al. Identification of interior fault position based on SVM and D-S evidence theory for electric transformer[J]. Electric Power Automation Equipment,2012,32(11):72-7.

[5] Zadeh L. Asimpie view of the Dempster-Shafer theory of evidence and its impiication for the ruie of combinatio[J]. AI Magazine,1986,7(1):85-90.

[6] LEFEVRE E, COLOT O, VANNOORENBERGHE P. Belief functions combination and conflict management[J]. Information Fusion,2002,3(2):149-162.

[7] 权文,王晓丹,王坚.一种基于置信最大熵模型的证据推理方法[J].控制与决策,2012,27(6):899-903. QUAN Wen, WANG Xiadan, WANG Jian. A combination rule of evidence theory based on brief max-entropy model[J]. Control and Decision,2012,27(6):899-903.

[8] 刘海燕,赵宗贵,刘熹.D-S证据理论中冲突证据的合成方法[J].电子科技大学学报,2008,37(5):701-704. LIU Haiyan, ZHAO Zonggui, LIU Xi. Combination of Conflict Evidences in D-S Theory[J]. Journal of University of Electonic science and Technology,2008,37(5):701-704.

[9] Murphy C K. Combining beiief functions when evidence confiict[J]. Decision Support Systems,2000,29(1):1-9.

[10] 邓勇,施文康,朱振福.一种有效处理冲突证据的组合方法[J].红外与毫米波学报.2004,23(1):27-32. DENG Yong, SHI Wenkang, ZHU Zhenfu. Efficient combination approach of confilict evidence[J]. Journal Infrared Millimeter and Waves,2004,23(1):27-32.

[11] 韩德强,邓勇,韩崇昭.利用不确定度的冲突证据组合[J].控制理论与应用,2011,28(6):788-792. HAN Deqiang, DENG Yong, HAN Chongzhao. Conflicting evidence combination by using uncertainty degree[J]. Control Theory & Applications,2011,28(6):788-792.

[12] 鲁峰,黄金泉.基于灰色关联聚类的特征提取算法[J].系统工程理论与实践,2012,32(4):872-876. LU Feng, HUANG Jinquan. Feature extraction algorithm of clustering based on grey relational theory[J]. Systems Engineering — Theory & Practice,2012,32(4):872-876.

[13] 柏丹丹,和敬涵,王小君.基于灰色关联分析的自适应低频减载[J].电力系统保护与控制,2014,42(6):20-25. BAI Dandan, HE Jinghan, WANG Xiaojun. Adaptive UFLS scheme based on grey correlation analysis[J]. Power System Protection and Control,2014,42(6):20-25.

Evidence Combination Method Based on Degree of Gray Relationship

LU Yanlong WANG Tuo XU Hong

(College of Electronics and Information Engineering, Xi’an Jiaotong University, Xi’an 710049)

In this paper, the shortage of D-S evidence theory as well as its modification are analyzed, then a new combination method based on degree of gray relationship is proposed. The method uses degree of gray relationship as evaluation criteria, then regards each piece of evidence as discrete points and computes the similarity between every two evidences in evidence collection. Then the obtained similarity which represents the importance of evidences is normalized. The similarity obtained above is regarded as the weight of every evidence and generate new evidence model. Finally fusion result is got by means of evidence model.The numerical examples show that the method proposed in this paper compared to other methods has following advantages, including fast convergent rate, simple calculation method, easy realization in a project.

D-S evidence theory, conflict evidence, degree of gray relationship, information fusion

2016年7月9日,

2016年8月28日

国家自然科学基金(编号:61071217);江苏省自然科学基金(编号:Bk0141216)资助。

卢彦龙,男,硕士研究生,研究方向:数据融合、图像处理。王拓,男,教授,博士生导师,研究方向:图像处理,智能电网。徐宏,男,硕士研究生,研究方向:数据融合、文本处理。

TP301.6

10.3969/j.issn.1672-9722.2017.01.012