基于改进蚁群算法的通信业务智能调配分析研究*

缪巍巍 吴海洋 施 健 吕顺利

(1.江苏省电力公司 南京 210024)(2.南京南瑞集团公司 南京 210003)



基于改进蚁群算法的通信业务智能调配分析研究*

缪巍巍1吴海洋1施 健2吕顺利2

(1.江苏省电力公司 南京 210024)(2.南京南瑞集团公司 南京 210003)

电力通信光传输网络的业务路由调配符合多约束条件的路由路径特点,传统的路由计算方法难以实现最优化的业务路径生成。论文在蚁群算法的基础上借鉴A*算法的思想,提出了一种改进的蚁群算法,有效避免了蚁群算法中杂乱搜索和容易导致局部最优的缺陷。通过实验仿真,改进后的蚁群算法在不同的网络拓扑图上均能得到较优解,验证了算法的稳定性和优越性,具有较好的可行性和实用性,可为通信业务的智能调配提供辅助分析支持。

电力通信网; 智能调配; 蚁群算法; A*算法

Class Number TP391

1 引言

随着智能电网和“三集五大”体系的全面推进,电力企业对于通信业务的需求呈现爆发式增长的趋势。电力通信网作为电力系统的专用网络,其承载的通信业务主要是与电力生产、运行相关的通信业务,包括继电保护业务、稳定控制业务、远动业务、调度业务、办公业务等,这些业务对路径选择、可靠性等方面有特殊要求,业务路由的不同调配方式可能会对电力系统的安全稳定运行带来不同的潜在风险。因此,针对电力通信的网络拓扑架构和当前通信业务的需求分布,在保证网络资源有效利用的同时,科学合理地调配与选择路由路径,使得通信业务能够获得满足其服务要求的传输路径,已成为增强网络运维效能、提升网络运维水平的重要工作[1]。

通信业务的路由调配是图论研究中的一个经典算法问题,路径选择由于其日益广泛的应用而倍受关注。专家们从不同的视角审视这个问题,并提出了很多算法,同时也对这些算法进行了改进。计算路由路径的常用算法[2～6]有传统的Dijkstra算法、floyd算法以及启发式算法如A*算法、蚁群算法、遗传算法等。由于电力通信业务的路由调配不是简单的选择最短路径,而是需要考虑众多约束条件,因此在具有两个或两个以上的约束条件或者所求顶点数较多的情况下,传统的Dijkstra算法和Floyd算法就不再具有优势。当赋权拓扑图中存在大量顶点时,传统的搜索算法均需要对图中所有顶点进行迭代遍历,耗费时间长,得到的也不一定是最优解。目前常用的算法是蚁群算法,或蚁群算法与其他算法相结合的混合算法,如蚁群算法和遗传算法结合。但是该算法存在着搜索杂乱和容易陷入局部最优的缺陷,同时多个启发式算法的组合又产生了很多不确定性。

针对上述存在的缺点,本文提出了一种改进的蚁群算法。针对蚁群算法中由于初始信息素浓度相同所带来的初期蚂蚁运动随机性问题,借鉴了A*算法的思想,以当前节点到目的节点的距离为参考,使蚂蚁寻食具有一定的方向性;同时根据求解质量的不同在信息素更新时,赋予不同的权值,从而增加解空间的多样性,并采用全局更新机制,改善了蚁群算法中容易陷入局部最优的问题。最后通过与其他搜索算法的比较,验证了本算法的可行性和实用性。

2 A*算法基本原理

A*算法[7～10]在人工智能中是一种典型的启发式搜索算法,其算法被广泛地应用于很多领域。A*算法的基本思想是从搜索空间的初始节点开始,先广度优先搜索,再用估价函数f(i)对该轮搜索到的各个子节点进行评估,选出最佳子节点,再从这个最佳子节点开始进行新一轮的启发式搜索直到目标节点为止。可见A*算法中最为关键的部分是其评估函数[6]的设计,该函数在保留了传统算法中只考虑已发生行为对问题影响的同时,增加了将发生行为对问题的影响度。评估函数f(i)的公式定义如下所示:

f(i)=g(i)+h(i)

(1)

式中,f(i)是评估函数,g(i)是初始节点s到当前节点i的实际代价度量,h(i)是从当前节点i到目标节点e的最小代价启发值。由于g(i)是直接计算出来,而h(i)却需要依靠对问题特性的经验估计来确定。针对不同的问题类型,h(i)的设计方式会有所不同,h(i)设计的优劣将直接关系到该评估函数f(i)的优劣,而f(i)设计的好坏则直接决定着该A*算法的性能优劣。f(i)越小,表示选择节点i所需要花费的代价越小,节点i被选择的概率也就越大。因此,在A*算法中f(i)的设计至关重要。在通信业务路由路径设计中,h(i)一般用欧式距离式(2)或曼哈顿距离式(3)表示均满足可采纳要求:

(2)

h(i)=|xG-xi|+|yG-yi|+|zG-zi|

(3)

在针对网络的最短路径计算问题中,通过添加从当前节点到目的节点的距离作为参考,使得搜索过程能够始终朝着距离目的节点较近的节点进行,搜索过程更具有目的性和方向性。因此,A*算法在搜索区域上会优于传统的搜索算法,有效避免了传统搜索算法杂乱搜索导致的搜索范围大、耗时长的缺点。

3 基于蚁群算法的改进算法

3.1 蚁群算法杂乱搜索的改进

在传统的蚁群算法寻路算法中,蚁群k(k=1,2,3,…,n)在t时刻从当前节点i寻找下一个节点j时的状态转移概率为

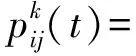
(4)

其中,allowed=C-tabuk,表示蚁群k(k=1,2,3,…,n)下一步允许选择的节点集合,α是信息素启发式因子,用于表征信息素重要程度的参数,反映了蚁群在运动过程中所积累的信息素在蚂蚁运动时所起的作用。β是期望启发式因子,用于表征启发函数重要程度的参数,反映了蚂蚁在运动过程中启发信息在蚂蚁选择路径中的受重视程度。ηij(t)为启发式函数,其表达式如下所示:

(5)

传统的蚁群算法未能充分利用启发式函数ηij(t),将其与通信网络的最短路由求解紧密结合起来。在式(5)中,启发式函数ηij(t)只考虑了上一节点到当前节点所付出的代价,并没有考虑当前节点到目的节点的代价,借鉴A*算法的思想,在启发式函数ηij(t)中新增两个参数dje(t)和γ。dje(t)表示当前节点j到目的节点e的最小代价。启发因子γ用于区别启发式函数中已经实际付出的g(i)和将付出的最小代价h(i)对蚂蚁寻找路径的重要性。修正后的启发式函数ηij(t)如下所示:

(6)

将式(6)替换到式(4)中,得到修正后的概率转移公式:

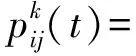
(7)

3.2 蚁群算法蚁群算法杂乱搜索的改进

当采取局部更新机制时,能够在一定程度上实现快速的信息素积累,同时可给其他蚂蚁的寻路过程提供经验值,但却容易造成局部最优,且这需要对每一只蚂蚁每走一步均要进行信息素的更新,运算代价较大。针对局部更新机制存在的缺点,本文采用全局更新机制的蚁周模型,同时引入权值参数λ,可根据每只蚂蚁寻找到的路径的优劣赋予不同的权值。根据权值的不同,对蚂蚁所走路径上的信息素浓度进行不同程度的更新,有效地改善了蚁群混合算法中的局部最优问题。

(8)

式中,Q表示的是信息素强度,是一个正的常数值,l(xk(t))表示蚁群k(k=1,2,3,…,n)在本次循环中所走的总路径长度,从上式可见,信息素强度Q与路径总长度l(xk(t))成反比例关系。

改进后的更新机制将判断每只蚂蚁每次所走路径是否接近最优路径,当蚂蚁所寻找的路径很接近最优解时就相应的增加信息素浓度,加快收敛的速度;如果蚂蚁搜索到的解的质量不高或者很差时就不对该路径的信息素浓度更新,或者只赋予一个很小的信息素增量值,避免对蚂蚁寻找最短路径造成干扰。

本文采用每次蚂蚁所走路径的长度与平均路径长度进行比较来寻找最优解。若所走路径长度大于平均值,则说明有偏离最优解的趋势,这时将赋予一个较小的权值或0;若所走路径长度小于平均值,则说明有朝向最优解的趋势,这时将赋予一个较大的权值。因此,权值参数λ表达式如下:

(9)

则改进后的蚁群算法信息素增量的更新机制变为

(10)

改进后的信息素更新机制采用全局更新避免了局部更新容易造成的局部最优现象,同时通过引入权值λ可智能地根据蚁群所寻路径的解的质量不同赋予不同的值,有效加快了蚁群向最优解收敛的速度。

改进后的蚁群算法流程步骤如图1所示。

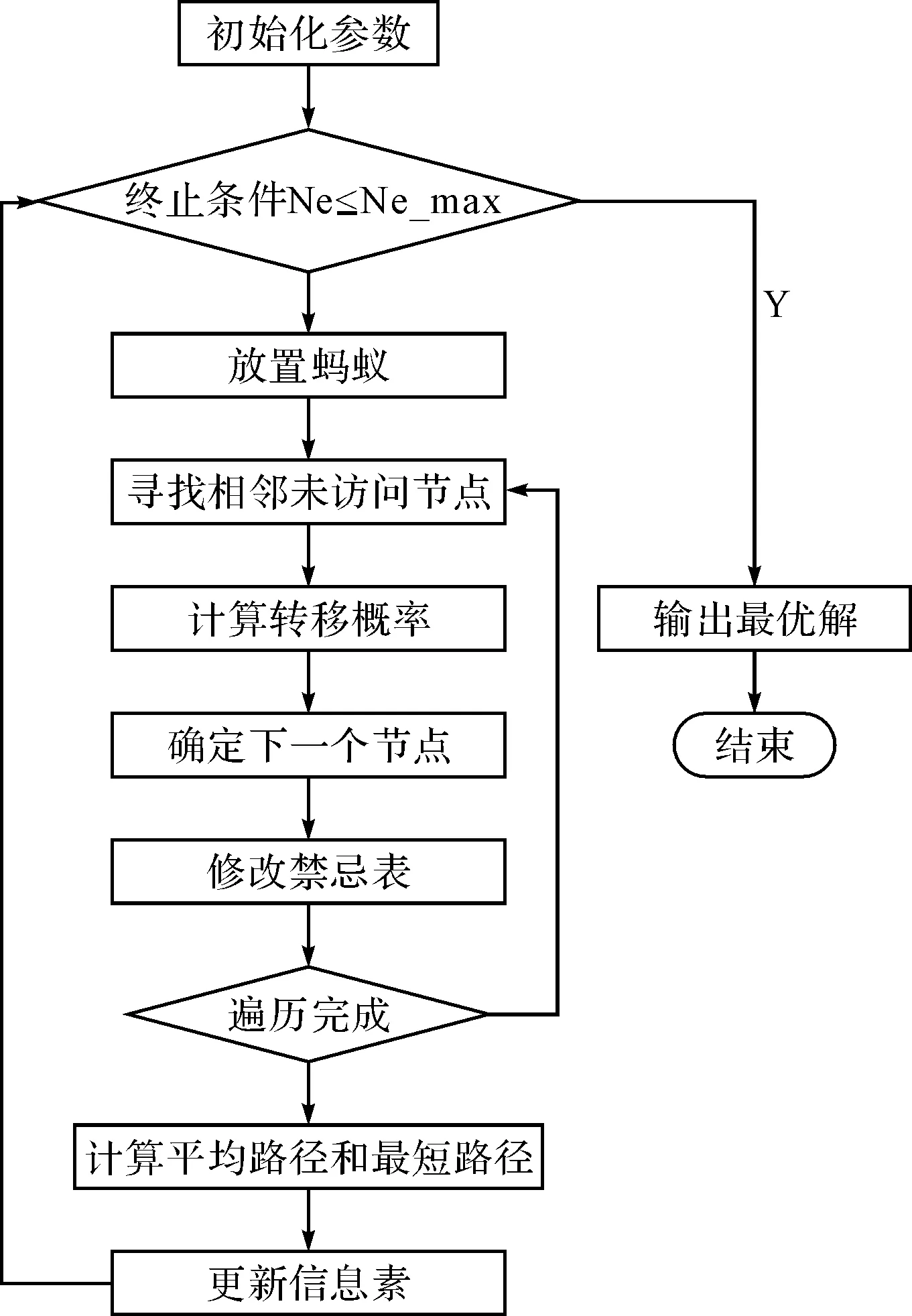
图1 改进蚁群算法流程

1) 初始化。初始化蚁群算法的信息素浓度。

2) 判断蚁群算法是否结束,即是否达到最大迭代次数Ne_max。如果达到迭代次数则结束,转到步骤8),否则转到步骤3)。

3) 放置蚂蚁。根据问题的规模,随机放置一定数量的蚂蚁。

4) 蚂蚁寻路。蚂蚁寻找相邻近的未访问节点,通过计算转移概率,确定下一个节点。

5) 修改禁忌表。在蚂蚁寻找路径的过程中动态的修改禁忌表表(Tabu),已经访问过的节点避免重复访问。

6) 遍历完成。判断蚂蚁是否遍历了所有节点,或者寻找到了目的节点,若是执行步骤7),否则跳转到步骤4)继续寻路。

7) 信息素的更新。计算平均路径和最短路径,并根据信息素的更新机制对信息素进行更新。

8) 输出最优解。

4 算法验证与比较

4.1 算法验证

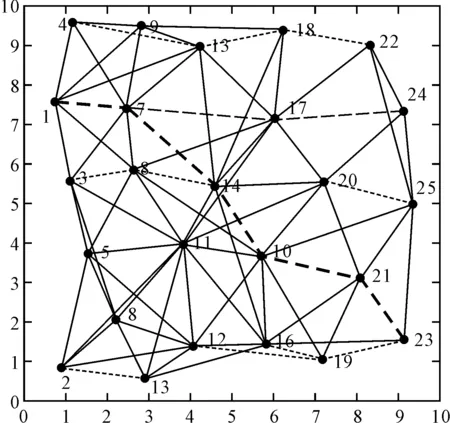
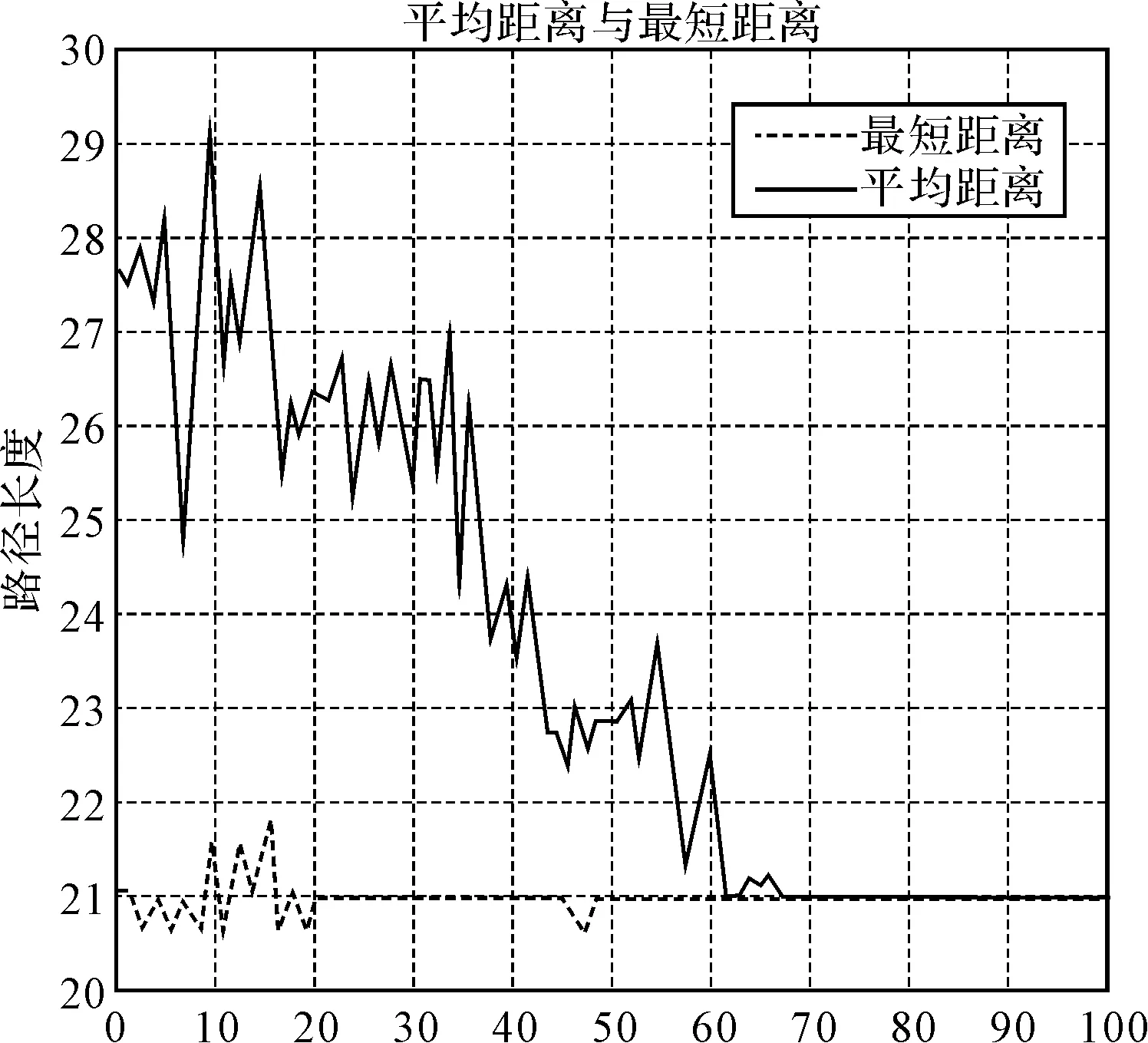
图2 传统蚁群算法的最短路径以及收敛曲线图

本文利用Waxman拓扑生成器,随机生成25个节点的网络拓扑模型,设置节点1为起始节点,节点23为目标节点。在此拓扑模型的基础上运行传统的蚁群算法,其经过迭代计算后得到的最短路径及收敛曲线图如图2所示,加粗线条即为传统的蚁群算法最终找到的最优路径。

在相同的网络拓扑模型上运行改进后的蚁群算法,其经过迭代计算后得到的最短路往以及收敛曲线如图3如下,加粗线条即为改进后的蚁群算法最终寻找的最优路径。

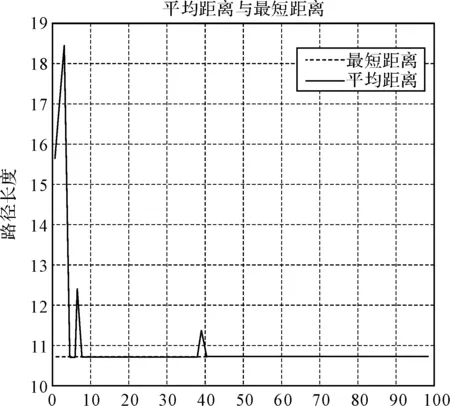
图3 改进蚁群算法的最短路径以及收敛曲线图

从以上两幅图对比可见,改进后的蚁群算法其搜索到的路径明显优于传统的蚁群算法。同时,改进后的蚁群算法收敛速度明显优于传统算法,提高了算法效率。

4.2 算法比较

基于图论最短路由计算的经典算法主要有Dijkstra算法和floyd算法。本文从算法的时间复杂度和空问复杂度两个维度将改进后的蚁群算法与这两种经典算法进行横向比较。Dijkstra算法是用来求解一个指定顶点到图中所有其他顶点间的最短路径,若要求解任意点到点的单播路由时需要对每一个网元节点重复使用Dijkstra算法,即增加一个for循环,导致和Floyd算法的时间复杂度一样。在matlab中,数据是以数组的方式进行存储的,所以每个算法的空间复杂度是一样的,由分析知,三者之间的区别具体如表1所示。

表1 算法比较

从上表可以看出三种常用算法的空间复杂度是一样的,而从时间复杂度上来比较时,对于求出所有顶点问的最短路径来讲Dijkstra算法和Floyd算法是一样的,而与蚁群算法比较三者的数量级是一样的,区别在于Nc,m的取值,通过对Nc,m进行合理的取值,可以降低算法的时间复杂度。

为验证实际算法效率,本文使用拓扑生成器随机依次生成网元数量为10、20、30、40、50、60、70、80、90、100的拓扑图,并分别使用Dijkstra算法、Floyd算法和蚁群算法依次对这些拓扑图求解,最后计算每个算法对不同网元数量的拓扑图求解所耗平均时间。

图4 三种算法平均耗时比较

图中为了比较的统一性将Nc,m的取值分别固定为50和60。从图4中可以看出,使用Dijkstra算法和Floyd算法求解任意点到点的单播路由时所耗时间相差不大。蚁群算法与Dijkstra算法和Floyd算法比较,在网元数量较少时耗时比较长,而当网元数量逐渐增多时蚁群算法的优越性就体现出来,因为Dijkstra算法和Floyd算法需要对所有来访问的节点进行权值更新,当网元数量很多时,计算量就比较大,从而导致算法的计算时间比较长。再加上蚁群算法是一种智能仿生算法,它具有快速的并行计算能力和正反馈机制,能够以信息素的形式对多个参数进行统一处理。这些是Dijkstra算法和Floyd算法所不具有的。因此,在求解多约束条件下的通信网络业务智能调配时使用蚁群算法是比较有优势的。

5 结语

本文对通信业务智能调配过程中经常使用的传统蚁群算法进行了分析与研究,针对蚁群算法中存在的杂乱搜索和局部最优的缺陷,改进后的蚁群算法借鉴了A*算法的思想,综合考虑了从当前节点到起始节点所花费的代价,增加了从当前节点到目标节点将花费的代价作为参考,使得蚂蚁搜索具有了方向性和目的性。与此同时,在信息素更新时采用了全局更新机制,增加了一个自适应参数,可根据蚂蚁寻找到路径的优劣程度赋予不同的权值,避免了局部更新机制所导致的局部最优解问题。

最后利用仿真环境对蚁群算法和改进后的蚁群算法进行验证,实验结果表明改进后的蚁群算法可较好的解决了蚁群算法中存在的杂乱搜索和局部最优的缺陷。同时,在复杂网络条件下的算法效率比传统路由算法也有较大的提升。

本文提出了改进的蚁群算法,求解业务路由的效率和质量较高,对于通信业务的智能调配具有较强的实用性。但该算法中很多参数的取值均需根据通信网络的实际情况在大量实验总结的基础上才能确定最优值,后续研究工作中应着力开展这方面的研究工作,确保实验结果更加有效和完善。

[1] ZHENG Rong-rong, ZHAO Zi-yan, LIU Shi, et al. Importance Based Power Communication Service Routing Assignment Algorithm[J]. Electric Power Information Technology,2012,10:23-28.

[2] Dijkstra E W. ANoteonTwoProblemsinConnection withGraphs[J]. Numer Math,1959(1):269-271.

[3] Kang Hwan, Lee, Byunghee, Kim Kabil. Pathplanning algorithm using the particle swarm optimization and the improved dijkstra algorithm[J]. Proceedings-2008Pacific-Asia. Workshop on Computational Intelligence and Industrial Application, PACIIA,2008:1002-1004.

[4] Gang LIU, Ramakrishnan G.A*Prune: An Algorithm for Finding K Shortest Paths Subjectto Multiple Constraints[J]. Proceedings IEEE INFOCOM,2001(2):743-749.

[5] Anwar M A. Integrating Knowledge-Base and Dijkstra’S Algorithmfor Finding Best Alternate Route Dynamically[C]//Multi Topic Conference, 2003. INMIC 2003. 7th International[S.1]: the IEEE Press,2003:428-433.

[6] Dai Zhiquan, Guan Yong, Guan Ran. Dynamic Adjustment A* Routing Algorithm[C]//2010 International Conference on Innovative Computing and Communication and 2010 Asia-Pacific Conference on Information Technology and Ocean Engineering,2010:316-318.

[7] Aini. A, Salehipour. A. Speedingup the Floyd—Warshall algorithmforthecycledshortestpathproblem[J]. Applied Mathematics Letters,2011,25(1):1-5.

[8] Nannicini, G., Delling, D., Liberti, L., et al. Bidirectional A* search for time-dependent fast paths[C]//WEA 2008. LNCS,2008:334-346.

[9] Wen Cao, Hui Shi, Shulong Zhu, et al. Applicationof AnImproved A* Algorithmin RoutePlanning[C]//WRIGlobal Congress, China, Xiamen,2009:253-257.

[10] Dorigo M, Maniezzno V, Colorni A. The ant System: Optimization by a cooperating agents[J]. IEEE Transcation on Systems Man and Cybernatic,1996,26(1):29-41.

Intelligent Allocation of Communication Services Based on Improved Ant Colony Algorithm

MIAO Weiwei1WU Haiyang1SHI Jian2LV Sunli2

(1. Jiangsu Provincial Power Company, Nanjing 210024)(2. Nanjing NARI Group Corporation, Nanjing 210003)

The traffic routing deployment of power communication optical transmission network is in accordance with the characteristics of the multi constraint conditions, and the traditional routing algorithm is difficult to achieve the optimization of the business path generation. Based on the ant colony algorithm, this paper proposes an improved ant colony algorithm based on the idea of A* algorithm, which effectively avoids the defects of random search and easily lead to local optimum in the ant colony algorithm. Through the simulation experiment, the improved ant colony algorithm in different network topology can obtain a better solution, verify the stability of the algorithm and the superiority, has good feasibility and practicability for deployment of intelligent communication services provide supplementary analysis support.

power communication network, intelligent allocation, ant colony algorithm, A* algorithm

2016年7月12日,

2016年8月28日

缪巍巍,男,硕士研究生,高级工程师,研究方向:电力通信传输网络、智能电网、通信网络运维。吴海洋,男,博士研究生,工程师,研究方向:电力通信网络、模式识别、信号处理。施健,男,硕士研究生,高级工程师,研究方向:通信网管、专家系统。吕顺利,男,硕士研究生,高级工程师,研究方向:电力自动化、智能电网、通信运维。

TP391

10.3969/j.issn.1672-9722.2017.01.009