基于LabVIEW的自整定PID控制器设计与分析

关艳翠　赵硕伟　杨振元

摘 要：为进一步提高工业控制效果，本文引入LabVIEW工程开发平台，利用其提供给的友好人机交互界面和较强的数据采集与处理功能对基于继电反馈的PID控制器展开了详细的设计。仿真分析结果表明，基于LabVIEW的自整定PID控制器设计能够有效提高工业生产的控制效果，具有良好的使用与推广价值。

关键词：工业过程控制；LabVIEW；自整定PID控制器

DOI：10.16640/j.cnki.37-1222/t.2017.02.193

1 继电反馈PID自整定技术分析

首先，对PID控制器的基本结构进行分析。反馈控制系统中，以y和ysp分别表示系统输出和预先设定值，以e=ysp-y表示控制误差，u表示控制信号[1]。给出如式1所示的经典PID控制器传递函数：

Gc（s）=KP（1++s） （1）

其中，KP、和分别表示比例增益、微分时间和积分时间。需要说明的是，因不同工业控制领域对PID控制器的性能要求具有较大差异，故应对其结构进行针对性改动从而确保达到预期控制效果。通常情况下，实际应用中的PID控制器大都被进行了微分增益的限幅，由此，其传递函数可改写为如下形式：

Gc（s）=KP（1++） （2）

其次，给出机电反馈PID的自整定法相关原理。机电反馈PID自整定法是以非参数模型辨识为依托的自整定法，该方法中，具有机电特性的非线性控制被相应的闭环控制回路所引入，以达到使被控过程产生极限环振荡的目的，同时，以得到的极限环振荡曲线为依据获得相应模型的特征参数，简单说来就是获取模型的振荡周期与临界比例系数Ku和Tu，在此基础上，借助Z-N临界比例度的参数整定表实现具体的PID参数计算。待整个自整定控制结束后，反馈控制系统将自动切换到PID控制模式。

2 基于LabVIEW PID控制器的设计

2.1 PID控制器设计

PID控制器设计流程如下：LabVIEW首先变换其采集的被控过程输出量的具体标度，而后，将变换后的标度值与设定值进行比较。需要说明的是，在自整定开始后，如果输出量超出了期望值，则可将其等效于继电器在关闭状态下输出的电压幅值（以m表示）；如果输出量小于期望值，则可将其等效于继电器在导通状态下输出的电压幅值（以M表示。其次，LabVIEW会对控制量施加转换操作，从而生成PWM波，生成的PWM波在抵达相应的模拟输出通道后，继电器在关闭和导通状态下的电压幅值m和M的占空比则分别为0和100%[2]。在自整定过程结束后，平台则根据对应的极限环振荡曲线对被控对象的特征参数，即Ku和Tu进行计算，而后，利用Z-N临界比例度对PID控制器参数予以计算，并将算得的参数传至PID自整定控制器中用以切换PID自动控制模块。

2.2 LabVIEW程序设计

基于LabVIEW的PID控制器设计中，平台程序的设计主要包括以下两方面工作：（1）前面板设计。用户同程序实现对接的接口便是LabVIEW的前面板程序，设计人员可利用LabVIEW创建相应的图形化界面，在确保该界面友好的基础上，增加结果分析的直观性。以自整定PID控制器VI前面板程序框图为依据，利用该程序，控制人员可实现对不同被控过程输出波形的同步获取[3]。

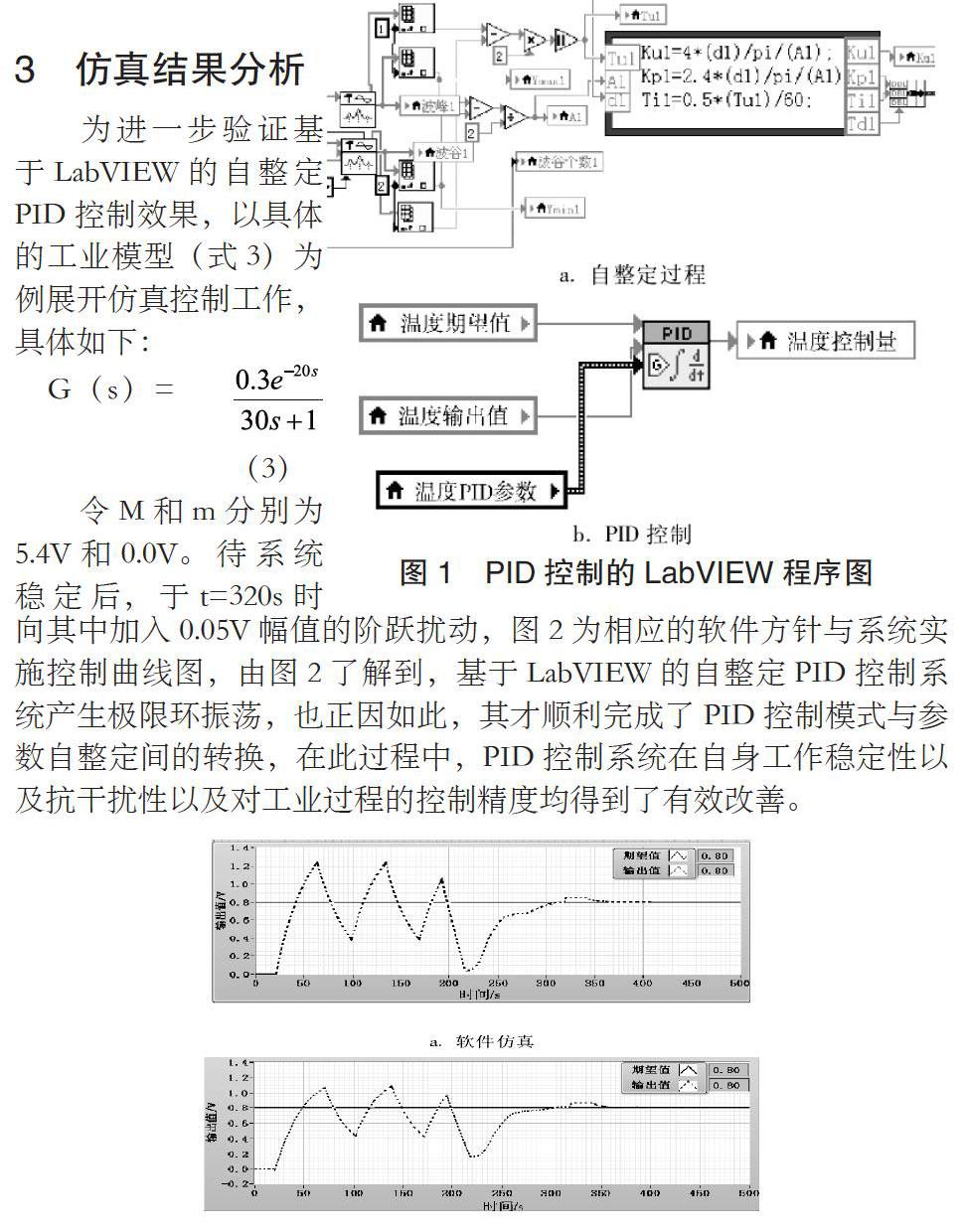
程序框图设计。前面板对象的控制可借助程序框图的编程来实现，而程序执行顺序的最直接的影响因素则为对应节点的数据流向。设计過程中，可利用程序框图中节点的数据流向形成对前面板I/O量的控制，以保证程序可以个人根据事先设定的功能顺利运行。基于LabVIEW的自整定PID控制程序框图如图1所示，其中，a图表示采集的数据与前面板输入数据的预处理和自整定过程，b图为系统进入PID控制模式。

3 仿真结果分析

为进一步验证基于LabVIEW的自整定PID控制效果，以具体的工业模型（式3）为例展开仿真控制工作，具体如下：

G（s）= （3）

令M和m分别为5.4V和0.0V。待系统稳定后，于t=320s时向其中加入0.05V幅值的阶跃扰动，图2为相应的软件方针与系统实施控制曲线图，由图2了解到，基于LabVIEW的自整定PID控制系统产生极限环振荡，也正因如此，其才顺利完成了PID控制模式与参数自整定间的转换，在此过程中，PID控制系统在自身工作稳定性以及抗干扰性以及对工业过程的控制精度均得到了有效改善。

4 结论

本文设计的LabVIEW自整定PID控制器的仿真结果表明，以LabVIEW作为平台支撑的自整定PID控制器无论在对工业过程控制的适应性和稳定性方面，还是对工业控制过程的控制精度与干扰性方面均具有良好效果。未来，还需进一步加强对基于LabVIEW自整定PID控制器的设计与研究，为提高工业过程控制效果，促进工业产业健康、稳定发展提供可靠的技术保障。

参考文献：

[1]肖奇军，李胜勇.模糊自整定PID控制器设计以及MATLAB仿真分析[J].计算机仿真，2013，09（15）：242-244.