基于三角模糊故障树分析的隧道工程风险评估——以马峦山隧道洞口施工为例

林如天李志高吴波，2

(1．福建工程学院土木工程学院福建福州350108;2．广西大学土木建筑工程学院南宁530004)

基于三角模糊故障树分析的隧道工程风险评估
——以马峦山隧道洞口施工为例

林如天1李志高1吴波1，2

(1．福建工程学院土木工程学院福建福州350108;2．广西大学土木建筑工程学院南宁530004)

为了使隧道洞口施工风险得到有效控制，建立了马峦山隧道洞口失稳的故障树，利用三角模糊数理论，确定了洞口失稳底事件的概率和重要度。同时引入模糊成本重要度的概念，结合提出的风险等级表，对马峦山隧道洞口失稳风险进行了评估。评估结果表明:洞口施工的总体风险等级为“Ⅱ级中度风险”;在10个风险事件中，3个为“Ⅱ级中度风险”，7个为“Ⅰ级，低度风险”。

三角模糊故障树;模糊成本重要度;洞口失稳;安全风险评估

0 引言

近年来，我国加大了公路铁路的建设力度，隧道建设也变得越来越平常。但是隧道工程一旦发生事故，往往会造成巨大的经济损失和人员伤亡，并且由于隧道工程的“一次性”特点，使得施工安全管理显得尤为重要。而风险评估是风险管理中重要的一环，它为风险管理的展开起指导作用。运用合理的评估方法对隧道工程进行风险估计，是防范事故频发的有力保障。

国际隧道协会的《隧道工程管理指南》［1］推荐使用的分析方法之一，是故障树分析法(FTA)。它是一种逻辑演绎法，以一种树状的图形呈现，反应了各个故障树事件之间的因果逻辑关系。它虽然有极强的定性分析能力，但在处理不确定性问题时，能力略显不足。因此学者们引入了模糊数学来增强故障树的分析能力。李青［2］等阐述了故障树分析从精确到模糊的重要度分析法，提出了重要度分析方法的新方法——中值法，代替传统使用的重心法，为故障树敏感性分析提供了一种便为可靠且便于操作的方法;林池峰［3］提出了模糊成本重要度的概念，并综合比较了采用模糊成本重要度分析和传统故障树分析的差别，证明了在敏感性分析中考虑经济损失的重要性。赵东安［4］在博士毕业论文中采用模糊故障树对盾构管片上浮、错台和破裂进行了风险分析，在考虑模糊成本重要度基础上进行了敏感性分析，并找出了其中的重要影响因素。郑俊杰［5］提出了三角、正态模糊数的精确求解方法，并对各种评估结果进行了比较，证明了改进三角模糊模型的优越性。以上文献虽对模糊故障树的应用进行了深入研究，理论基础十分雄厚，但最终的评估结果往往只停留在敏感性分析，不能体现专项评估结果和总体风险评估的关系，对于工程实际问题的解决不能发挥其全部作用。

本文针对这个问题，在已有的理论基础上，对采用三角模糊数实施的总体风险评估进行了研究，提出了基于模糊成本重要度的风险等级标准，并以实际工程为依托，对隧道工程洞口施工进行风险评估，证明了评估系统的合理性与实用性，为隧道工程风险管理的研究提供参考。

1 基本理论

基于三角模糊故障树理论，风险评估模型可以按照以下步骤建立。

1.1 故障树顶事件的选择

故障树的顶事件是一个系统分析的出发点，是一个源头，一般是项目中最不希望发生的事件。该项目将山岭隧道洞口施工失稳作为故障树的顶事件。

1.2 故障树的建立

故障树的建立一般使用人工演绎法。为使之后的运算更为简便可将故障树进行删减或转换，即进行规范化处理［6］，使得故障树中只含有“与门”“或门”和“非门”这三种逻辑门。在对本文案例马峦山隧道洞施工进行安全风险分析时，利用WBS－RBS法识别出容易造成重大危害的风险源，作为故障树的底事件。在概率分析中假设各风险源是相互独立的，且任意风险事件的发生都会导致顶事件的发生。即建立一个由最小割集［6］单一事件组成的或门结构故障树。

1.3 模糊数学在故障树分析中的应用

在传统的故障树中，底事件的概率往往是一个精确值，使得顶事件的计算结果也是一个精确值。但在实际工程中受各种干扰因素的影响，一些底事件不能被精确表达，因干扰因素存在而造成各种误差。在一个庞大的故障树中往往会造成误差的累积，得出的顶事件概率会为一个失效的数值［7］。所以在研究中，学者们为底事件引入了模糊数的概念，使得误差在合理的范围内，从而使顶事件的结果更加精确。

1.3.1 三角模糊数

三角模糊数是为了解决不确定环境下的问题而产生的方法。由Zadeh在1965年提出Dev模糊集的概念，并应用于质量管理、风险管理中。在三角模糊数(triangular fuzzy number)中对任何x∈u，都有一个数μ(x)∈［0，1］与之对应，μ(x)称为x对u的隶属度，μ称为x的隶属函数。其隶属度函数和隶属曲线分别如公式(1)和图1所示。

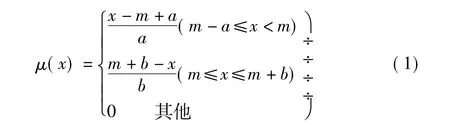
1.3.2 三角模糊数的模糊算子

在引入三角模糊理论后，用模糊数~Ai来代替底事件的概率，同时使用模糊算子来表达系统逻辑关系，这样得到的顶事件概率也是模糊数［8］。

底事件的发生概率采用模糊处理时，故障树逻辑与门、或门的模糊算子表示为［9］:

(1)与门

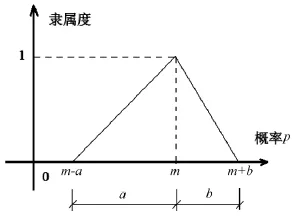
图1 三角模糊数的隶属度函数曲线

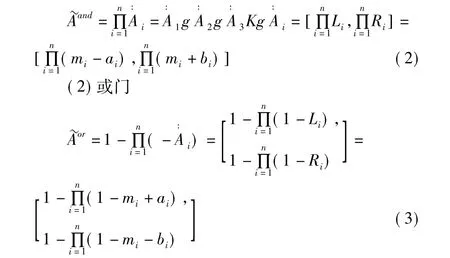
1.3.3 模糊重要度

重要度是评判底事件重要程度的一个指标，即敏感性分析，它可以分析出众多底事件对系统的贡献程度，或者称为该事件对系统运作的贡献程度。掌握这一数据可以很快地掌握系统中的薄弱环节，对系统的安全稳定性进行改进。

在一个模糊数主导的故障树中，模糊重要度的计算方法有:Hideo Tanaka的模糊重要度计算法、重心法、中值法等。分析各个方法的适用程度，本文选用“中值法”。即对于有界的闭模糊数，令A1=，存在点m，使得该点为分界线，模糊数曲线下的左、右两部分面积相等。则称m为该模糊数的中值。

STi=mT－mTi＞0为故障事件xi的模糊重要度。mT为所有底事件发生时顶事件T的中值;mTi为底事件xi不发生时，顶事件Ti的中值［2］。如果ST≥STi，则认为事件xi比事件xj重要，亦事件xi对系统的影响大于xj对系统的影响。因此，如果要改进系统，则首先应该考虑改进事件xi。

1.3.4 施工安全风险评估标准

本文在评估施工安全风险时，引入模糊重要度成本的概念［3］，并进一步放大损失在风险评估中的比重，用模糊损失重要度Cj替换原式中的经济损失比cj，其计算公式如式(4):

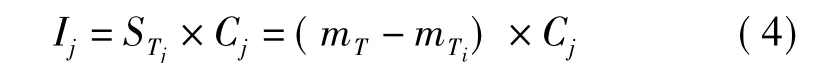
式中，Ij为模糊成本重要度;STi为第j项风险的模糊重要度;Cj为第j项风险的模糊损失重要度(用中值法直接计算)。通过模糊成本重要度，查阅风险等级标准(表1)，可得各底事件的风险等级，依据最大隶属度原则得到总体风险等级。

表1 风险等级标准

2 案例分析

通过查阅相关资料［10～13］，并对马峦山隧道进行调研后，列出该隧道较容易发生也最容易产生重大危害的10个风险源进行研究，其风险源如下:(1)初期支护不及时;(2)初期支护参数不符合设计要求;(3)开挖循环步距过大;(4)超挖;(5)二次衬砌不符合时机;(6)边仰坡开挖未按设计要求坡度施工;(7)洞顶及洞口排水系统未及时形成;(8)施工扰动;(9)洞口边坡有裂缝未能及时处理;(10)钢拱架架设时支撑不牢。建立的马峦山洞口失稳故障树，如图2所示。

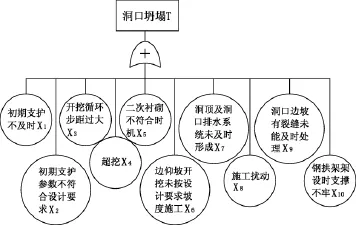
图2 马峦山隧道洞口故障树分析图

根据专家调查(自然语言模糊化详见文献［14］)，得到马峦山隧道洞口开挖时各风险发生概率和成本损失概率，并将其转化为等腰三角模糊数。其中，各风险的平均值及为等腰三角模糊数的模糊中值，拟模糊区间为±10％，在公式(1)中表现为:ai=bi=10％，i∈［1.10］。再结合马峦山洞口施工故障树，如图2所示，按照上文顺序将风险源记为X1～X10，计算各风险的均值和经济损失比，如表2所示。

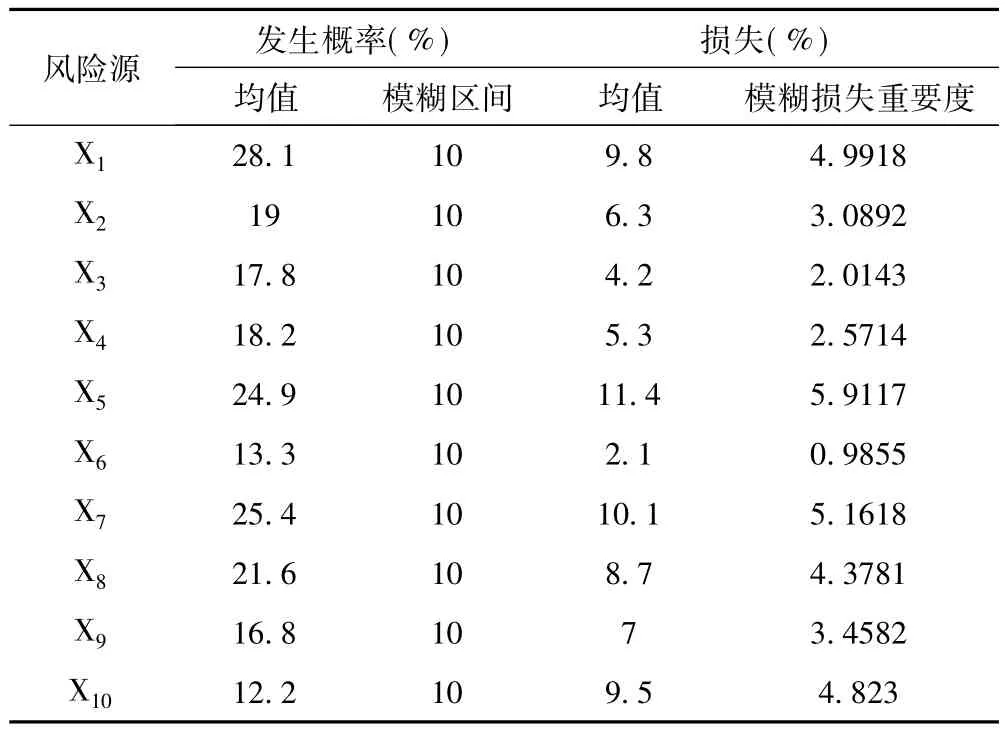
表2 各风险的模糊概率和模糊损失重要度

依据章节1.3.3计算各风险事件的重要度STi。以底事件X1为例，其重要度ST1计算过程如公式(5)所示:

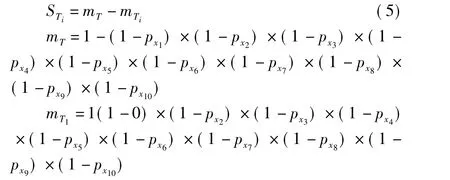
考虑全部风险时的顶事件隶属曲线和中值及不考虑事件“初期支护不及时”，顶事件的隶属曲线和中值图像分别如图3～图4所示。

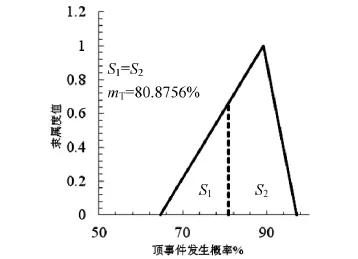
图3 考虑全部风险时的顶事件隶属曲线和中值

依据章节1.3.2中模糊算子计算公式(3)，将各底事件的左模糊值Ln、右模糊值Rn和平均值An代入运算，即可求得底事件X1的重要度为0.047 911。依照此法可求得马峦山洞口施工，底事件X1～X10的模糊重要度、模糊成本重要度和排序，如表3所示。

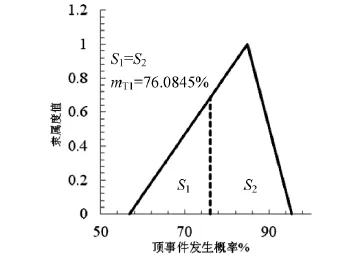
图4 不考虑事件“初期支护不及时”，顶事件的隶属曲线和中值

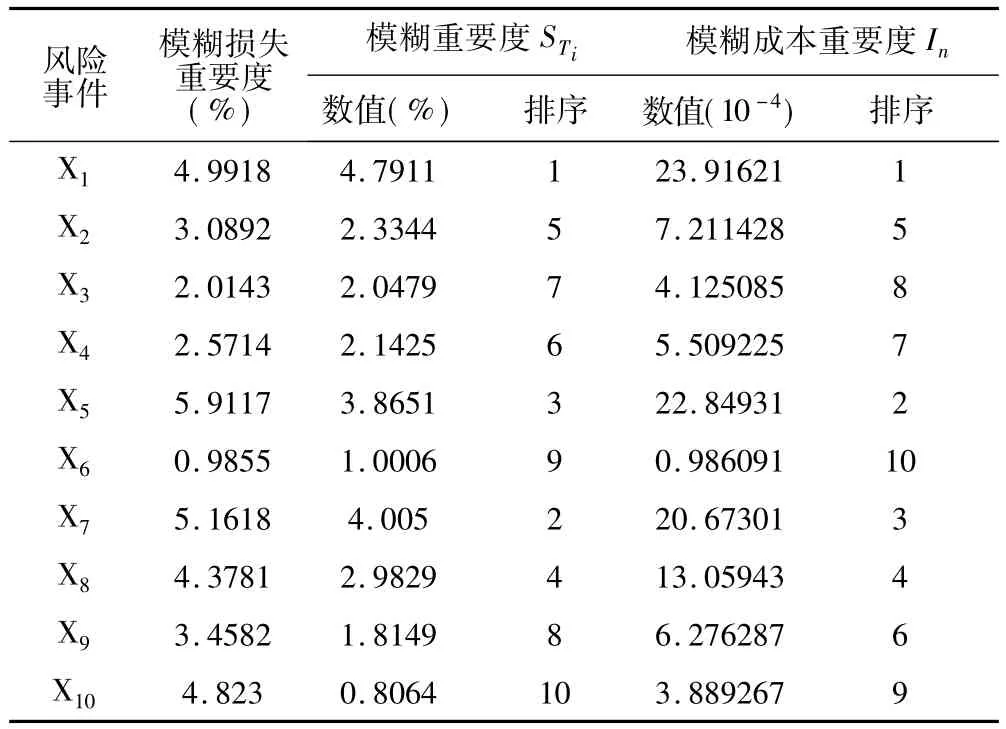
表3 各风险事件的重要度、模糊成本重要度和排序

结合表3风险等级标准，对马峦山洞口施工专项风险和总体风险进行评估:风险事件“二次衬砌不符合时机”“初期支护不及时”以及“洞顶及洞口排水系统未及时形成”风险等级为“Ⅱ级中度风险”;其余风险事件为“Ⅰ级低度风险”;依据最大隶属度原则马峦山洞口施工总体风险等级为“Ⅱ级中度风险”。

由评估结果可知，在马峦山洞口施工中，风险“二次衬砌不符合时机”“初期支护不及时”“洞顶及洞口排水系统未及时形成”对洞口施工安全有一定的影响，属于可接受风险，一般不需要采取风险处理措施，但需要予以监测。

3 结论

(1)文章针对隧道工程风险的模糊性与不确定性，应用了三角模糊数的故障树评估方法，对隧道洞口施工安全风险进行评估。甄选出10个在洞口施工中容易发生危险的事件，建立了马峦山洞口失稳的故障树模型。同时引入了成本模糊重要度的概念，兼顾了发生概率P和损失C对评估结果的共同影响，使定量分析结果更加精确可靠。

(2)给出了模糊成本重要度的风险等级标准，完善了模糊故障树在工程风险评估中的应用。为基于模糊故障树系统工程项目的专项评估和总体评估提供了参考，且便于应用到工程实际中。

(3)应用三角模糊故障树模型对马峦山隧道洞口施工安全进行了评估。得出洞口失稳的总体风险等级为“Ⅱ级中度风险”。其中风险事件“二次衬砌不符合时机”“初期支护不及时”“洞顶及洞口排水系统未及时形成”为“Ⅱ级中度风险”;其余7个事件风险等级为“Ⅰ级低度风险”。这与现场检测结果较为吻合，证明了该评估系统的合理性与实用性。

［1］Eskesen S D，Tengborg P，Kampmann J，et al．Guidelines for tunnelling risk management:International Tunnelling Association，Working Group No．2［J］．Tunnelling＆Underground Space Technology，2004，19(3):217－237．

［2］李青，陆廷金．模糊重要度分析方法的研究［J］．模糊系统与数学，2000(1):89－93．

［3］林池峰．基于模糊事故树的盾构隧道施工成本风险分析［D］．武汉:华中科技大学，2009．

［4］赵冬安．基于故障树法的地铁施工安全风险分析［D］．武汉:华中科技大学，2011．

［5］郑俊杰，林池峰，赵冬安，等．基于模糊故障树的盾构隧道施工成本风险评估［J］．岩土工程学报，2011(4):501－508．

［6］Eskesen S D，Tengborg P，Kampmann J，et al．Guidelines for tunnelling risk management:International Tunnelling Association，Working Group No．2［J］．Tunnelling＆Underground Space Technology，2004，19(3):217－237．

［8］杨伦标，高英仪．模糊数学原理及应用［M］．广州:华南理工大学出版社，1996．

［9］易昊旻，周生路，吴绍华，等．基于正态模糊数的区域土壤重金属污染综合评价［J］．环境科学学报，2013(4): 1127－1134．

［10］许崇帮，田海宁，周宁．鳌峰山隧道洞口段风险源辨识与风险评估分析［J］．公路交通科技，2012(10):96－101．

［11］吴坚，黄俊，李升连，等．基于专家调查法的公路隧道洞口失稳风险分析［J］．地下空间与工程学报，2009(S1): 1407－1411．

［12］中国公路学报编辑部．中国隧道工程学术研究综述· 2015［J］．中国公路学报，2015(5):1－65．

［13］陈龙，黄宏伟．软土盾构隧道施工期风险损失分析［J］．地下空间与工程学报，2006(1):74－78．

［14］郑俊杰，赵冬安，林池峰．三角模糊数故障树法在盾构隧道成本分析中的应用［J］．土木工程与管理学报，2012(4):1－5.

Risk assessment of tunnel engineering based on triangular fuzzy fault tree analysis in Maluan mountain tunnel portal construction

LIN Rutian1LI Zhigao1WU Bo1，2
(1．School of Civil Engineering，Fujian University of Technology，Fuzhou 350108; 2College of Civil Engineering and Architecture，Guangxi University，Nanning 530004)

This paper established the fault tree for portal instability of Maluan mountain tunnel，using triangular fuzzy number theory，which figured out the probability and the importance degree of those selected key events of the hole collapses for controlling the risk of tunnel portal construction effectively.In addition，it introduced a concept of fuzzy cost importance that evaluated the Maluan mountain tunnel instability，combined with the risk rating table.Shown as the evaluation results:the overall risk level for the construction of the portal is“levelⅡ，moderate risk”;in those selected ten key events，three of them are evaluated for“levelⅡ，moderate risk”and seven of them are“levelⅠ，low risk”.

Triangular fuzzy fault tree;Fuzzy cost importance;Portal instability;Security risk assessment

U45

:A

:1004－6135(2017)01－0072－04

国家自然科学基金项目(51478118)，福建省自然科学基金项目(2014J01170)

林如天(1991．9－)，男。

E-mail:472795697@qq．com

2016－10－16