基于距离场的二维偏移曲线快速生成方法

秦 睿，刘圣军，陈子泰，袁炜雄，张 帆，刘新儒*

(1. 中南大学 工程建模与科学计算研究所， 湖南 长沙 410083; 2. 中南大学 数学与统计学院， 湖南 长沙 410083)

基于距离场的二维偏移曲线快速生成方法

秦 睿1,2，刘圣军1,2，陈子泰1,2，袁炜雄1,2，张 帆1,2，刘新儒1,2*

(1. 中南大学 工程建模与科学计算研究所， 湖南 长沙 410083; 2. 中南大学 数学与统计学院， 湖南 长沙 410083)

提出了一种快速生成二维偏移曲线的方法.对于无自相交的二维多边形曲线，该方法能构造无自相交、保留准确尖锐特征的二维等距偏移曲线.算法的基本思想：先在一个均匀网格上根据给定的曲线采样一个局部有向距离场，然后使用等值线抽取方法从有向距离场中获取偏移曲线.在构造局部距离场时引入3个过滤器,在远离偏移曲线的区域消除大量冗余计算.采用经典MS(marching square)方法抽取初始多边形偏移曲线，通过一个混合解析解和二分搜索方法，快速计算得到偏移曲线与网格边的准确交点.根据最近点位置信息对初始多边形偏移曲线进行简化和特征重构(如尖角和圆弧)，构造无自相交、顶点数少、具有尖锐特征、含混合直线和圆弧段的准确偏移曲线.大量数据实例说明该方法性能良好.

偏移曲线；距离场；无自相交；过滤器；解析法

Fast construction of 2D offset curve based on distance field.Journal of Zhejiang University(Science Edition), 2017,44(1):010-021

0 引 言

二维曲线偏移广泛应用于平面几何造型、型腔加工和分层加工[1-3]，可生成轮廓线平行的刀具路径.然而，曲线偏移是一项困难的几何操作.CAD/CAM软件迫切需要快速稳定的偏移算法.

现有的经典二维曲线偏移算法包括基于边偏移的算法[4-8]和基于点偏移的算法[9-13].通常，偏移操作会导致在偏移曲线中出现无效问题，最终的偏移曲线是去除无效偏移段的结果.但大部分算法都存在无法处理的案例(见图1).LIN等[10]提出了一种基于卡圆解决局部无效问题的方法，尽管此方法通过修剪内角大于180°的偏移线可减小偏移曲线的逼近误差，但当形状复杂时很难生成准确的偏移曲线，见图1(e).

本文提出一种基于距离场的准确等距曲线快速构造方法，无须处理自相交和局部无效问题.等距偏移曲线Lr实际上由平面上到原始曲线L的最短距离为r的所有点构成，偏移距离为r的等距偏移曲线Lr可采用以下隐函数表示：

f(p)=dis(p,L)-r=0,

(1)

其中，p为平面上偏移曲线Lr上的点，dis(p,L)为返回平面上点到给定曲线L的有向距离的函数，正值表示点p在曲线内部，负值则表示在曲线外部，曲线L的顶点按逆时针方向排列.偏移值r可以是正值或负值，只要计算偏移曲线周围局部区域内的网格点即可，所以本文需在均匀网格上构造局部有向距离场.构造的3个过滤器用于在局部有向距离场的计算中消除冗余计算；在抽取偏移曲线的过程中，提出了一种结合解析法和二分法的快速计算网格边与等距曲线交点的混合算法；为了获得顶点数少且保留尖锐特征的准确等值线，设计了一个后处理过程以改进MS算法[15]的初始结果.

本文的主要贡献：

(1)采用基于距离场的隐式函数定义二维等距偏移曲线，避免了局部无效和自相交问题；

(2)使用3个过滤器：分层扫掠圆片过滤器、内/外过滤器和四叉树过滤器，加速了局部有向距离场的计算，可消除92.9%～94.3%的冗余距离计算；

(3)引入一种结合解析计算和二分搜索的混合方法，用于计算隐式偏移曲线与网格边的交点，较经典的二分搜索法其计算效率有很大提高.

(4)基于最近点所在原始曲线中的信息，对初始偏移曲线进行简化，最终形成由较少直线段和圆弧段构成的偏移曲线，同时重构了尖锐特征和准确偏移曲线.

图1 实例展示现有方法的不足Fig.1 Examples showing the limitations of the existing methods(a)基于边偏移的方法，需要解决自相交和不连续性问题[4-8];(b)文献[14]失败的例子;(c)文献[11-12]失败的例子;(d)文献[13]误判的例子;(e)文献[10]生成不准确的等距曲线，即使经过截断，其中虚线圆弧段为准确偏移线，黑色点横线为算法执行过程中给定曲线的更新.(a)The method based on edge shifting, with the problems about self-intersection and disjoint[4-8]. (b),(c),(d) are the failed cases for [14], [11-12], and [13], respectively. (e)The inexact offset curve generated by [10], even be trimmed, where the dashed arcs are the exact offsets, and the black dash dot lines are the updated curve for the original during the algorithm processing.

1 相关工作

研究者提出了多种二维曲线偏移算法，早期的研究工作可参考文献[16-17].有关二维曲线偏移算法的主要工作可归纳为：基于Voronoi图的算法[14,18-20]、基于边偏移的算法[4-8]和基于点偏移的算法[9-13].

当偏移曲线所在区域已知时，使用边界的Voronoi图，只要简单连接每一个区域的偏移曲线段即可.PRESSON[18]引入Voronoi图生成无岛且被线段包围的轮廓平行刀具路径.HELD等[19]在此基础上进行了改进，提出了使用Voronoi图处理带岛的曲线.LAI等[14]提出了一个基于向前位置跟踪的无效环剔除算法.在他们的工作中，所有的退化曲线段都可通过Voronoi图消除.而无效环的剔除则通过将二维交点遍历问题转换为一维区间识别问题.然而，当曲线相邻的2个内角之和大于180°且偏移距离较大时，他们使用的Voronoi图方法会出错，如图1(b)所示.另外，尽管通过构造Voronoi图可以避免自相交，但这些方法只适用于形状相对简单的曲线，且有数值误差，特别是接近圆弧的区域.

基于边偏移的方法是逻辑上最直接和简单的一类偏移曲线生成方法，其基本思想是以给定的偏移距离沿着法向方向偏移每一条线段的起点和终点.这类方法的主要缺陷是需要检测和解决所有自相交和不连续性问题(如图1(a)所示).文献[5-7]提出了基于分段干涉测试的偏移方法，将所有线段分为整体干涉、部分干涉和反向干涉3类，定义了2个操作并对干涉线段进行处理.然而，除干涉问题外，还要解决曲线在偏移方向上内角大于180°引起的偏移曲线不连续问题.文献[8]除了可以应用于数控加工刀具路径的生成过程外，更多是应用于计算机图形学.他们的主要贡献是可处理自相交、重叠和小圆弧问题.初始偏移曲线采用基本的分段偏移获得，本文主要研究局部问题的处理.一条轮廓线通常包含成千上万条直线段，非常耗时，因此不适合数控加工领域.

基于点偏移的方法是通过在每个顶点的角平分线上选择偏移点，使之到相邻2条线段的距离为偏移距离，然后根据原始给定曲线的顶点连接关系顺次连接各顶点对应的偏移点，得到偏移曲线.不同方法之间的差异主要在于偏移曲线上无效部分的去除.WONG等[9]在采用角平分线方法生成初始偏移曲线时，如果相邻2条角平分线相交，那么他们之间的线段将被删除，通过其相连的2条边构造新的角平分线.通过检测环的方向判定全局环的有效性，与原始曲线方向相反的则为无效环，将其从偏移曲线中剔除.文中没有详细给出对局部无效环进行剔除的算法.LIN等[10]受文献[9]的启发，提出了基于卡圈的方法解决由相邻角平分线相交造成的局部无效问题.通过卡圈及相应的规则，采用不同的三边模板对原始给定曲线进行更新，从而生成无局部无效段的偏移曲线.最后，采用树分析过程收集所有全局有效环，得到最终的偏移曲线.文献[11-12]通过比较偏移边与对应原始边的方向以确定无效边，通过去除无效偏移边以解决局部无效问题，通过检查环的方向确定和去除全局无效环.但此算法无法处理图1(c)所示的无效问题.LEE等[13]在解决局部无效问题时，除了验证偏移边的方向有效性外，还验证了偏移边的位置有效性.但他们用偏移边2个端点的有效性决定偏移边的有效性是不合适的，如图1(d)所示.尽管文献[13]给出了处理无效问题的5种不同判例，但仍未包含所有判例，导致文献[13]方法无法实现正确的曲线偏移.基于点偏移的方法虽不会生成不连续的偏移曲线，但由于局部无效和全局无效的检测和处理非常复杂，即使采用文献[10]的方法，生成的偏移曲线也不准确，如图1(e)所示.

采用基于距离场的方法生成二维偏移曲线[21]和三维偏移曲面[22]，可避免前述方法出现的偏移曲线自相交、不连续及无效检测与处理的问题.文献[21]将偏移问题定义为求解初值为原始给定曲线的偏微分方程，并采用快速跟踪方法得到方程的解.该方法在求解过程中，网格点处的距离值是所采用小包围盒边长或对角线的求和，而不是准确的到原始给定曲线的距离，导致最后得到的解是一条近似偏移曲线.文献[22]通过设计4个过滤器快速计算局部三维距离场，然后采用一种改进的等值面抽取方法生成三角网格模型的偏移曲面.偏移曲面采用三角片网格表示，精度越高，其三角片数量越多，对后续处理的影响越大.本文基于文献[22]的思想求解二维偏移曲线问题.针对曲线计算过程中主要涉及点与直线段、直线段与直线段之间的距离，设计了与直线段或多边形相关的3个过滤器，以快速实现局部二维距离场创建，并设计混合解析法和二分法的偏移曲线与网格边的交点计算方法，从而实现0.25 s内生成一条偏移曲线.最后，通过简化曲线实现与原始给定曲线顶点个数相近且保持尖锐特征的准确偏移曲线.

2 算法概述

在实际工程应用中，如分层加工，轮廓线通过平面与给定工件实体模型求交得到，因而是一条或多条带内环的无自相交的封闭多边形曲线.对于这类曲线，目标是获得无自相交的偏移曲线并保留其尖锐特征.算法分3步：

(1)将给定的多边形曲线L嵌入到一个包围它和偏移曲线的空间中.该空间在均匀网格上被采样成一个偏移曲线Lr周围窄带区域的局部有向距离场.设计了3个过滤器用于快速计算距离场，见第4节.

(2)计算网格边和偏移曲线的交点.根据网格边与原始曲线之间的位置关系，推导了解析计算交点的公式，并与二分搜索法结合形成一个快速计算交点的混合方法，见第5节.

(3)设计了一个简化及特征重构过程，生成保留尖锐特征的无自相交的等距偏移曲线.并使用圆弧和直线段对偏移曲线进行简化，获得了更准确的曲线偏移结果，见第6节.

图2给出了本文算法框架的主要步骤.局部距离场采样在均匀分布的网格上，最小距离计算和交点计算均可在多核计算机上并行处理，方法简单且易于实现.

图2 算法框架Fig.2 The method framework(a)嵌入到一个均匀剖分的网格中，对给定的二维多边形曲线，计算局部距离场；(b)找到有效网格边，计算偏移曲线与网格边的交点；(c)抽取出等距偏移曲线；(d)简化和特征重构生成准确等距曲线.(a)A given 2D polygon embedded in a uniform grid, and a local distance field based on the polygon. (b)Detecting valid grid edges and computing the intersections between them and the offset curve. (c)Extracting the offset curve. (d)Simplifying the initial extracted offset curve and reconstructing the shape features for the exact offset curve.

3 局部距离场快速构造

为了在一个n×n的均匀剖分网格上构造给定曲线L的有向距离场，最直接的方法是计算(n+1)2个网格节点到曲线L的最短距离.网格点p到曲线L的最短距离可通过计算其到曲线L上所有线段距离中的最小值获得.在找到点p在曲线L上的最近点pc后，两点之间有向距离的符号就可以通过点p处于曲线所包围区域的内部还是外部判断.有许多方法可以实现点与多边形位置关系的判定，如射线法、累计角度法、编码法等.本文采用角度加权法向[23]来快速判断点与多边形的内外关系.此方法尽管可以快速确定距离的符号，但最近点的计算非常耗时，尤其当n非常大时.下面介绍3个过滤器的加速计算.

3.1 分层扫掠圆片过滤器

扫掠圆片层次结构过滤器可用于点p到给定多边形曲线L距离的加速计算.基本思想是建立起曲线L上直线段的包围盒层次结构，使得远离点p的直线段不必进行距离计算测试.将文献[22]中的直线段扫掠包围球体改造为直线段扫掠包围圆片，应用于二维空间中点与曲线的最近距离计算.

不同于文献[24]需计算线段与线段之间的距离，本文只需计算点到直线段之间的距离.直线段可以表示成参数形式：

p(t)=p1+t(p2-p1)，

(2)

3.2 四叉树过滤器

尽管使用分层扫掠圆片过滤器可以快速计算函数f(p)，但在具有n2个结点的网格上构造距离场依然费时.实验显示，在一台个人电脑上使用扫掠圆片层次结构过滤器计算点p到具有1.2×103条边的直线的最近点，需要0.01 ms.当在具有5132个结点的网格上构造距离场时，需要2 632 ms.通常情况下，一条曲线的偏移曲线被包含在一系列的小网格内.只需要找到偏移曲线附近的这些小网格，构建一个窄带内的局部距离场，即可快速构造等距曲线.

在介绍包围盒层次结构过滤器之前，首先给出有(无)效网格点和有(无)效包围盒的概念.

定义1 对于任何网格结点，若其位置点p满足

(3)

其中s为小网格的边长，r为偏移距离，dis(·,·)表示点p到给定曲线L的有向距离，则称之为有效网格结点.否则，为无效网格结点.

如果直接检测每一个网格点是否有效，需计算点到给定曲线的距离.为了避免冗余计算，引入包围盒.将网格点分组，使之包含在具有更大边长的包围盒中，如图3(a)所示.

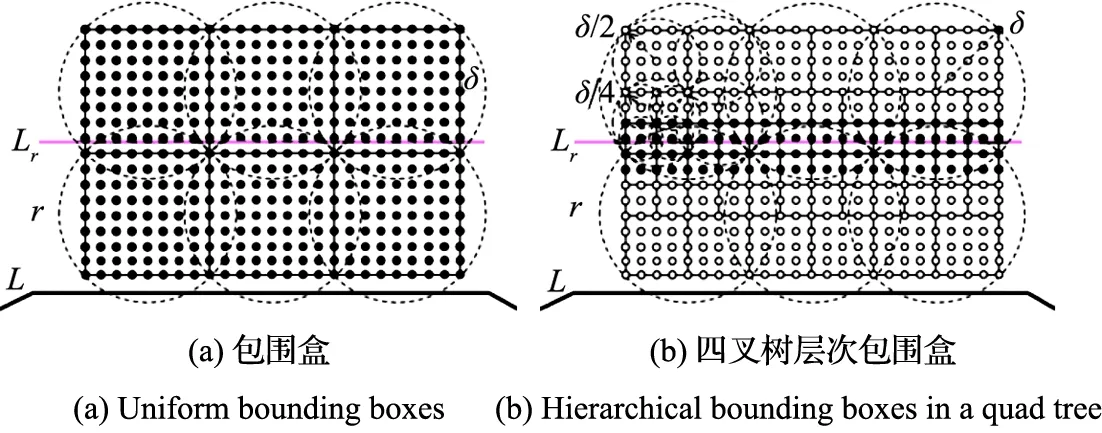
图3 四叉树过滤器示意图Fig.3 Quad-tree filter实心点为有效点，空心点为无效点.Solid points are valid, while empty points are invalid.

定义2 对于一个对角线长度为2δ的包围盒，若其中心cb到给定曲线L的距离满足

(4)

则称为无效包围盒.否则，称为有效包围盒.

由式(3)和(4)，可得在无效包围盒中的网格结点都是无效的.而在有效包围盒中，包含有效和无效网格结点.

尽管使用包围盒可以快速剔除无效网格点，但选择恰当大小的包围盒比较困难.当选择的包围盒太大时，有效包围盒中依然存在许多无效网格点.而当选择太小时，会增加大量有效性检测操作.为了更有效地剔除无效网格点，本文采用自适应分层包围盒过滤器——四叉树过滤器，如图3(b)所示.对于每一个有效包围盒B，对其一分为四，形成4个小的包围盒Bsub.计算小包围盒Bsub中心点到给定曲线的距离，若满足式(4)，则小包围盒Bsub不再细分，且所有包含于该小包围盒内的网格点被标记为无效.否则，Bsub将继续细分下去，直到包围盒所包含的网格点不多于4个.

3.3 内/外过滤器

根据偏移方向，确定偏移曲线处于给定曲线的内部还是外部.为了只在偏移曲线附近构建局部有向距离场，检测网格点或包围盒中心点到给定曲线的有向距离dis(p,L)，

dis(p,L)=sgn((p-pc)·nc)dmin,

(5)

其中nc为点p在给定曲线L上的最近点pc处的角度加权法向.

通常设定nc指向曲线L包围区域的外部.偏移距离r为正的偏移曲线Lr处于给定曲线L的外部，那么所有处于曲线L所包围区域内部的网格点为无效点；反之，偏移距离r为负的偏移曲线Lr处于给定曲线L的内部，那么所有处于曲线L包围区域外部的网格点为无效点.无效包围盒的判定应满足式(4).

4 网格边上等距曲线交点的快速计算

使用第3节介绍的3个过滤器，可以快速构造偏移曲线Lr附近的一个局部有向距离场f(p).不过，距离场内只计算了网格点上的有向距离值.根据这些有向距离值，能找到与偏移曲线相交的小网格.

定义3 在有向距离场中的2个有效网格点p1和p2之间的一条网格边e，若p1和p2满足

f(p1)f(p2)<0，

(6)

则称e为有效网格边.否则为无效网格边.

为了生成准确的偏移曲线，在应用MS算法抽取分段线性连续的初始偏移曲线的基础上，采用简化方法自动重构尖锐特征，减少结果偏移曲线的顶点数.在均匀网格上，MS算法计算有效网格边与隐式偏移曲线的交点，并记录交点在原始曲线上的最近点及其所在边的序号，以便用于曲线简化.有效网格边上的交点可通过求解下列方程得到：

f((1-α)p1+αp2)=0， 0≤α≤1.

(7)

由于函数f(·)中的有向距离函数是非线性的，方程(7)的解可以通过最简单但缓慢的二分搜索法得到.

为了加速交点计算，提出了结合解析法和二分搜索法的混合计算方法，并推导了交点的解析计算公式.

4.1 混合法

在实际造型时，只有当网格边足够短时，满足解析方法计算交点的条件的可能性才比较高.当不满足解析计算交点的条件时，则将网格边一分为二，找到交点可能存在的区段，然后测试该区段是否满足解析计算交点的条件.重复上述过程，直到找到交点.解析计算的交点将通过一次距离验证:

|dis(p,L)-r|≤ε，

(8)

其中ε=10-5为公差限.若距离偏差不小于ε，则将包含交点的区段进行一次二分，继续交点计算的过程.在实现中，二分搜索法的终止条件也为式(8).

根据以上描述，在算法1中列出了用混合法计算交点的基本步骤.

算法1 混合法计算交点

输入 有效网格边e的2个端点p1和p2，其相应最近点p1,c，p2,c和给定曲线L；

输出 交点p.

步骤：

(1)IFp1,c和p2,c在同一条线段上；

(2)使用解析法计算交点p(见5.2节)；

(3)ELSE；

(4)将网格边e一分为二，使用包含交点的新区段更新边e，同时更新p1、p2和相应最近点p1,c和p2,c，回到第(1)步；

(5)END IF；

(6)IF交点p满足式(8)；

(7) 输出交点p;

(8)ELSE；

(9)将网格边e一分为二，用包含交点的新区段更新边e，同时更新p1、p2和相应最近点p1,c和p2,c，回到第(1)步；

(10)END IF.

对处于线段2个端点位置的情况需要进一步计算，以便判断p1,c和p2,c是否在同一条线段上.因为最近点计算过程给出的结果可能是2个点不在同一条线段上，但属于下列情况之一：

(1)p1,c在线段l1内部，p2,c在与l1相邻的线段l2的一个端点v上，v也是l1的一个端点；

(2)p1,c和p2,c分别在2条不同线段的端点上，但这2个点是另外一条线段的2个端点.

4.2 解析解

对于2个端点p1和p2的最近点p1,c和p2,c处于同一条直线段上的有效边e，本节将给出其与偏移曲线Lr的交点p的解析计算公式.

分析发现，平面上线段l周围的一个点q，它在线段上的最近点qc将落在线段内部或线段的2个端点处.平面上线段l周围的区域通常被线段端点处的垂线分成3个区域，如图4(a)所示.

图4 偏移曲线与网格边交点解析计算示意图Fig.4 Illustration for analytically computing the intersections between the grid edges and the offset curve(a)一条线段与其2个端点处的垂线将平面分为3个区域；(b)处于线区域的线段;(c)处于端点区域的线段.(a)Three areas on the plane are divided by a line segment and the orthogonal lines are at its two end points； (b)The line area case; (c)The point area case.

定义4 平面上线段l周围的区域称为

(1)线区域，如果该区域内的所有点q的最近点都落在线段l内部，如图4(a)所示的区域2；

(2)点区域，如果该区域内的所有点q的最近点都落在线段l两个端点上，如图4(a)所示的区域1和3.

基于这个区域的分类，推导解析计算网格边与偏移曲线交点的公式.如果一条线段p1p2完全落在线段l的线区域内，如图4(b)所示，则交点p为

(9)

如果线段p1p2完全落在线段l的端点v对应的点区域内，如图4(c)所示，则交点p可以通过公式

(10)

计算，其中α∈[0,1].

尽管解析法可以快速计算偏移曲线与网格边的交点，但网格边通常会跨越多个区域.使用上述解析方法计算交点，需先将网格边e剖分为多段，使得每一子段都完全落在同一个区域内.如果一个子段的2个端点ps,1和ps,2满足f(ps,1)f(ps,2)>0，表明交点不在该子段上，舍去该子段.而对于满足f(ps,1)f(ps,2)<0的子段，在实现中则直接取第1个子段的交点，其余子段不予考虑.

5 准确偏移曲线的生成

在使用经典MS算法抽取第4节中得到的网格与偏移曲线交点的基础上，利用每个交点在原始多边形曲线上最近点的所在线段或端点的信息，简化与重构特征，获取准确的偏移曲线.

经典MS算法可以保证抽取的偏移曲线是无自相交的.但是，由于经典MS算法通过逐个处理每个小网格，连接每个小网格边上的交点得到偏移曲线，因而抽取的偏移曲线存在2个问题：(1)偏移曲线由许多条短直线段组成，即使这些直线段是在一条直线或一段圆弧上，顶点数亦太多；(2)连接交点成短直线段时没有考虑交点的法向信息，丢失了偏移曲线上的尖锐特征，导致生成的偏移曲线不准确.即使使用自适应网格生成的偏移曲线也无法完全解决上述问题.为此，设计了一个包含简化与特征重构的后处理过程.

对平面上的多边形曲线，其准确偏移曲线由直线段和圆弧段组合而成.其中，直线段由原始曲线中的直线段偏移得到，圆弧段则由原始曲线中的顶点偏移得到.基于平面偏移曲线的性质，在采用经典MS算法抽取初始的等距偏移多边形曲线之后，将考察偏移多边形曲线上所有顶点的最近点所在的原始曲线的边或顶点的信息，具有相同原始曲线的边或顶点信息的偏移多边形曲线上的所有相邻顶点将形成一条直线段或圆弧段.

在算法实现中，用(id1,id2)表示原始多边形曲线L的边和顶点信息，其中idk，k=1,2，为原始多边形曲线顶点的序号.顶点被认为是退化的边.例如，(3,4)表示一条2个端点在原始多边形曲线顶点序列中的序号分别为3和4的边，(4,4)表示一个序号为4的顶点.给定初始偏移曲线Lr上2个相邻顶点p1和p2的最近点所在原始多边形曲线的边或顶点的信息为(id1,id2)和(id3,id4)，

(1)如果id1=id3，id2=id4，且id1≠id2，则表示2个顶点是由原始多边形曲线L的同一条边上的点偏移生成，在偏移曲线Lr中处于同一条直线段上，图5(a)中红色虚线矩形框所包围的点；

(2)如果id1=id3，id2=id4，且id1=id2，则表示2个顶点由原始多边形曲线L的同一个顶点偏移生成，在偏移曲线Lr中处于同一圆弧段上，图5(a)中红色虚线椭圆框所包围的点；

(3)如果id1≠id3或id2≠id4，则表示2个顶点分别由原始多边形曲线L的3条边上的点或1条边与1个顶点或2个顶点偏移生成，偏移曲线Lr在这2个点之间会形成2条直线段或1条线段1条圆弧段或2条圆弧段的交点，如图5(a)所示绿色虚线椭圆框和蓝色虚线矩形框所包围的点.

通过式(1)和(2)减少偏移曲线上的顶点数，如图5(b)所示；由式(3)重构尖锐特征，生成准确的偏移曲线，如图5(c)所示.

图5 等距曲线简化与特征重构Fig.5 Offset curve simplification and feature reconstruction(a)抽取出的初始等距曲线，每一个顶点保留其最近点所在原始曲线中边的信息，并根据这些信息进行分组;(b)根据(a)的分组结果进行拼合，形成长的直线段并重构圆弧特征，减少顶点数；(c)根据交点最近点信息的变化，计算直线段之间.直线段与圆弧段，及圆弧段之间的交点，重构尖锐特征，生成准确的偏移曲线.(a)An extracted initial offset curve where all vertices are grouped with their closest points and relating original edges; (b)Longer line segment and arc features are recovered by merging the vertices according to the clusters, and vertices are reduced; (c)Sharp features are reconstructed and then an exact offset curve is generated according to the variations of the intersections computed between line segments, line segment and arc segment, and arc segments.

6 实验结果与讨论

使用VC++实现本文算法，并在普通配置的个人手提电脑上使用不同的数据实例进行算法测试.使用本文算法对不同的平面多边形曲线采用不同的偏移值进行向内和向外偏移，得到了一系列结果和统计数据，如图6、7和表1～4所示.

图6给出了采用本文方法在512×512网格上生成不同偏移距离并经过简化和特征重构的5条不同形状的偏移曲线，其中“手”“花”“京剧脸谱”“马”和“老鼠”曲线形状中分别包含188，1 303，1 831，1 781和2 075个顶点.5条不同形状曲线的给定距离偏移曲线的计算时间及误差的统计信息见表1.由表1可知，所有给定曲线的偏移曲线都可在不超过0.25 s的时间内生成.对抽取的初始偏移曲线进行简化及特征重构，可减少偏移曲线的顶点数,提高偏移曲线的逼近精度.由表2知，简化后的偏移曲线顶点数不到初始偏移曲线顶点数的25%，精度至少是初始偏移曲线的106倍，达到了10-8，基本上可以认为是准确偏移曲线.

图6 使用不同偏移距离进行偏移的结果Fig.6 Offsetting results with different offset distances网格分辨率512×512.The dimensions of the grid is 512×512.

图7 给定曲线形状在不同分辨率网格上使用不同偏移距离进行偏移的结果Fig.7 The offsetting results in different resolution grids with different offset distances for the given curve shapes其中，黑色实线为给定的曲线形状,第1行与第3行为初始偏移曲线，第2行与第4行为简化及特征重构后的偏移曲线.Here, the black curve are the given shapes, and the first and third rows are the initial offset curves while the second and fourth rows are the final offset results after simplification and feature reconstruction.

曲线形状顶点数偏移距离计算时间/msT1T2T3Ttol初始偏移曲线顶点数平均误差简化偏移曲线顶点数平均误差手188-2201091612519589．9×10-41510．00花1303-11161563220421861．3×10-33780．00脸谱1831-22151573120320401．4×10-33230．00马1781-25161873123424161．8×10-32052．2×10-9老鼠2075-25161723121922581．7×10-31918×10-10

注T1为构造扫掠圆片层次结构的时间，T2为分辨率为512×512的网格上构造距离场的时间，T3为抽取偏移曲线的时间，包括抽取初始偏移曲线和简化的时间，Ttol为前3项的总和.

当原始曲线采用一般样条曲线表时，可以先采用直线段自适应进行近似，转化成多边形曲线，然后使用本文算法进行处理.初始偏移曲线的简化依然可以提高偏移曲线的精度.

图7显示的是对2个形状复杂性不同的曲线在不同分辨率的网格上进行不同距离的偏移结果，同时给出了简化前后的曲线形状及顶点，顶点用红色进行标记.形状简单的“五角星”曲线包含10个顶点，偏移距离为25，而形状复杂的“猪”的曲线包含1 271个顶点，偏移距离为15.图中对于使用分辨率较高的网格生成的偏移曲线，由于顶点太多，无法显示曲线的顶点，见图7(d)和(e)的第1个和第3个图.图7中第1行与第3行为初始偏移曲线，第2行与第4行为对应简化及特征重构后的偏移曲线.由图7知，在分辨率较小的网格上，抽取出的初始偏移曲线丢失了尖锐特征，且圆弧特征的逼近很粗糙，如图7(a)第1和第3个结果所示.随着分辨率的增大，曲线上的尖锐特征逐步恢复，且圆弧特征的逼近精度逐渐改善，如图7(b)～(e)第1行和第3行所示.

表2 不同分辨率网格中生成偏移曲线的统计数据

从图7第2行和第4行的结果中发现，当采用分辨率较小的网格，如32×32，偏移曲线的简化和特征重构效果非常明显，尤其是对形状简单的曲线.在低分辨率的网格上对简单曲线构造的偏移曲线进行简化和特征重构，简化后的偏移曲线逼近精度比在高分辨率网格上构造的初始偏移曲线更高，且与它们的简化结果曲线相同，见图7第2行的偏移曲线，表2中的数据也说明了这点.所以使用本文方法在构造包含长直线段曲线的偏移曲线时，可先在低分辨率的网格上生成初始偏移曲线，然后进行简化.

为了研究本文提出的过滤器的性能，在构造局部距离场时测试了所能减少的最近距离计算次数.这里，最近距离计算指使用基于分层扫掠圆片过滤器的方法进行的点到曲线最近距离计算.分别对简单形状曲线“五角星”和复杂形状曲线“猪”在513×513的均匀划分网格上构造偏移曲线附件的窄带距离场.测试了4种过滤器组合形式：(1)只使用包围盒，m×m表示2个方向上使用m个包围盒；(2)使用包围盒和内/外过滤器；(3)四叉树过滤器；(4)使用内/外过滤器和四叉树过滤器.由表3的统计数据不难发现，使用内/外和四叉树过滤器可以剔除网格点上约92.9%～94.3%的无效计算.

测试了混合计算有效边上交点的算法效率.基于顶点数不同的曲线形状，表4统计了不同分辨率网格中具有交点的有效网格边数量.不难发现，98.5%的边使用混合方法可在不超过6次细分操作下找到交点，而使用二分查找法，只有不到20%的边能在不超过6次细分操作下找到交点.由此可见，混合方法大大提高了求交的效率.

表3 使用不同过滤器进行点到曲线最近距离计算次数的统计

图8 用本文方法对图1中的5种曲线生成准确的偏移曲线Fig.8 Exact offset curves generated by our method corresponding to five cases in Fig.1

曲线形状顶点数偏移距离分辨率有效边数混合方法0次二分1次二分2次二分小于6次二分法小于6次五角星1015128618611236170256124012303412390512248424745224840猪12711512847430663474672625695275587469491205121910171096541907375

本文方法能有效处理图1中文献[4-8,10-14]方法难以解决的问题，能生成连续、准确的偏移曲线.图8给出了本文方法处理对应于图1中示例的结果.黑实线为原始给定多边形曲线，浅色线为生成的偏移曲线.

表5给出了3条给定的原始曲线用本文和文献[10]方法生成的偏移曲线结果的比较.在生成偏移曲线过程中，本文方法采用了分辨率为512×512的均匀网格，因而耗时比文献[10]方法长.但依然能达到交互的计算速率，满足用户交互设计的要求.另外，本文方法生成的偏移曲线比文献[10]方法更准确，平均精度超过文献[10]100倍.图9给出了对应图形显示的比较结果,可明显看到，在内角大于180°处，本文方法生成的偏移曲线更光滑、准确.采用文献[10]程序生成结果时，发现只能处理内偏移，对较大偏移距离无法得到结果或所得结果错误.

7 结 论

提出了一种快速、鲁棒计算平面多边形曲线的无自相交、准确偏移曲线的方法.算法的基本思想是在一个均匀网格上基于给定曲线的局部有向距离场采样，然后利用等值线抽取算法得到偏移曲线.基于距离场的方法可以减少经典方法中对偏移曲线上某段有效性的判断及相关处理工作.通过使用3个过滤器消除在距离场构造过程中的大量冗余计算，从而高效生成局部有向距离场.采用经典的等值线抽取方法可以获得初始偏移曲线.在曲线抽取过程中，采用基于解析解和二分法的混合交点计算方法，大大缩短了查找过程，实现了等值线的快速抽取.在偏移曲线与网格边的交点计算过程中，根据保存的最近点的位置信息，用长直线段或圆弧段表示端点具有相同最近点位置信息的短线段，并进行合并.初始偏移曲线上相邻顶点的最近点位置信息的变化，标识了原始曲线中线段的变化，据此可在偏移曲线上计算相邻直线段之间、直线段与圆弧段、圆弧段之间的交点，以重构偏移曲线上的尖锐特征，最终获得准确的偏移曲线.文中的大量例子和统计数据都有力地说明了本方法的良好性能和优势.

[1] PHAM B. Offset curves and surfaces: A brief survey[J]. Computer-Aided Design,1992,24:223-239.

[2] MACKAWA T. An overview of offset curves and surfaces[J]. Computer-Aided Design,1992,31:165-173.

[3] LASEMI A, XUE D, GU P. Recent development in CNC machining of freeform surfaces: A state-of-the-art review[J]. Computer-Aided Design,2010,42:641-654.

[4] KIM K, JEONG J. Tool path generation for machining free-form pockets with islands[J]. Computers & Industrial Engineering,1995,28:399-407.

[5] CHOI B, PARK S. A pair wise offset algorithm for 2D point sequence curve[J]. Computer-Aided Design,1999,31(12):735-745.

[6] PARK S, CHOI B. Uncut free pocketing tool-paths generation using pair-wise offset algorithm[J]. Computer-Aided Design,2001,33:739-746.

[7] PARK S, CHUNG Y. Offset tool-path linking for pocket machining[J]. Computer-Aided Design,2002,34:299-308.

[8] LIU X Z, YONG J H, ZHENG G Q, et al. An offset algorithm for polyline curves[J]. Computers in Industry,2007,58:240-254.

[9] WONG T, WONG K. NC tool-path generation for arbitrary pockets with islands[J]. The International Journal of Advanced Manufacturing Technology,1996,12:174-179.

[10] LIN Z, FU J, HE Y, et al. A robust 2D point-sequence curve offset algorithm with multiple islands for contour-parallel tool path[J]. Computer-Aided Design,2013,45:657-670.

[11] KIM H, LEE S, YING M. A new offset algorithm for closed 2D lines with islands[J]. The International Journal of Advanced Manufacturing Technology,2006,29:1169-1177.

[12] KIM H. Tool path generation for contour parallel milling with incomplete mesh model[J]. The International Journal of Advanced Manufacturing Technology,2010,48:443-454.

[13] LEE C, PHAN T, KIM D. 2D curve offset algorithm for pockets with islands using a vertex offset[J]. International Journal of Precision Engineering and Manufacturing,2009(10):127-135.

[14] LAI Y, WU J, HUNG J, et al. A simple method for invalid loops removal of planar offset curves[J]. The International Journal of Advanced Manufacturing Technology,2006,27(1):1153-1162.

[15] MAPLE C. Geometric design and space planning using the marching squares and marching cube algorithms[C]//Proceedings of 2003 International Conference on Geometric Modeling and Graphics. London：Geometric Modeling and Graphics,2003:90-95.

[16] HATNA A, GRIEVE R J, BROOMHEAD P. Automatic CNC milling of pockets: Geometric and technological issues[J]. Computer Integrated Manufacturing System,1998,11:309-330.

[17] DRAGOMATZ D, MANN S. A classified bibliography of literature on NC milling path generation[J]. Computer-Aided Design,1997,29:239-247.

[18] PRESSON H. NC machining of arbitrarily shaped pockets[J]. Computer-Aided Design,1978,10:169-174.

[19] HELD M, LUKACS G, ANDO L. Pocket machining based on contour-parallel tool paths generated by means of proximity maps[J]. Computer-Aided Design,1994,26:189-203.

[20] BO Q. Recursive polygon offset computing for rapid prototyping applications based on Voronoi diagrams[J]. The International Journal of Advanced Manufacturing Technology,2010,49(9):1019-1028.

[21] DHANIK S, XIROUCHAKIS P. Contour parallel milling tool path generation for arbitrary pocket shape using a fast marching method [J]. The International Journal of Advanced Manufacturing Technology,2010,50(912):1101-1111.

[22] LIU S J, WANG C C L. Fast intersection-free offset surface generation from freeform models with triangular meshes[J]. IEEE Transactions on Automation Science and Engineering,2011,8(2):347-360.

[23] BAERENTZENJA, ANANAES H. Signed distance computation using the angle weighted pseudonormal[J]. IEEE Transactions on Visualization and Computer Graphics,2005,11(3):243-253.

[24] LARSEN E, GOTTSCHALK S, LIN M C, et al. Fast proximity queries with swept sphere volumes[C]//Proceedings of International Conference on Robotics and Automation. San Francisco：Technical Report of Department of Computer Science,1999:1-32.

QIN Rui1,2, LIU Shengjun1,2, CHEN Zitai1,2, YUAN Weixiong1,2, ZHANG Fan1,2, LIU Xinru1,2

(1.InstituteofEngineeringModelingandScientificComputing,CentralSouthUniversity,Changsha410083,China; 2.SchoolofMathematicsandStatistics,CentralSouthUniversity,Changsha410083,China)

A fast approach of generating a 2D offset curve from any polygonal curve is presented, which preserves sharp features and is self-intersection free. The basic idea is first to establish a local signed distance field on a uniform grid according to the input curve and then employ a contouring algorithm to extract the offset curve from the distance field. Three filters are conducted to generate a narrowband signed distance field around the offset curve in a very efficient way to reduce computation redundancies in regions far from the offset curves. The initial offset curve is derived by a traditional MS (Marching Square) method, the accurate intersections between the grid edges and the offset curve are computed quickly by a hybrid method employing the analytical solutions and the bisection search. Based on these closest points, an exact offset curve composed of line and arc segments is constructed by merging short line segments and reconstructing sharp features. The derived offset curve is intersection-free and retains the sharp features. The quality and performance of this approach are demonstrated by a number of experimental tests on various examples.

offset curve; distance field; intersection-free; filter; analytic solution

2016-07-25.

国家自然科学基金资助项目(61572527,61602524)；湖南省科技计划重点项目(2014FJ2008).

秦 睿(1995-)，ORCID:http://orcid.org/0000-0002-0914-5104，男，本科生，主要从事几何计算与优化算法研究.

*通信作者，ORCID:http://orcid.org/0000-0001-5427-0178，E-mail：liuxinru@csu.edu.cn.

10.3785/j.issn.1008-9497.2017.01.002

TP 391

A

1008-9497(2017)01-010-12