基于k-shell和信息熵冗余度的网络节点影响力度量

杜翠凤

1 引言

在社交网络中，营销人员希望通过具有影响力的客户使产品信息快速传播。随着通信技术的发展和在线社交网络的普及[1]，研究人员借助于在线社交互联网海量的交互信息以及用户之间的行为关系，构建各种网络节点的影响力度量模型。这些模型可以归纳为三类：基于拓扑结构的网络节点影响力度量；基于用户行为的网络节点影响力度量；基于用户交互信息的网络节点影响力度量。而本文考虑到通信数据的特点，将重点阐述适用于通信海量数据的网络拓扑结构的度量方法。

基于网络拓扑结构的度量方法从传统的以节点“中心性”[2]为代表的度量方法扩展到以局部网络结构[3-5]、全局网络结构[6-9]以及特征向量[10]为代表的度量方法。由于全局网络结构的评估方法具有较高的复杂度，并不适用于大规模社交网络节点度量，因此不少学者从局部角度实现节点影响力的度量。研究结果表明，k-shell（k-壳）在衡量海量社交数据的节点影响力上最为合适[7]，而PageRank等相关算法则不适用于处理无向网络[4]。因此，在节点度量方法的扩展性、普适性以及效率是影响力度量工作面临的巨大挑战。k-shell方法可快速识别网络中最有影响力的节点，但该方法所得到的核心层节点并不能真实反映其在网络的核心位置，这是由于核心层中某些节点携带的信息熵冗余度较高。针对该问题，本文结合信息熵冗余度判断核心层存在的冗余节点，采用基于k-shell和信息熵冗余度相结合的方法不仅能够保证核心点识别的速度，而且还可以提高核心点识别的精度。

2 网络影响力节点度量的相关研究

2.1 问题定义

网络影响力节点度量是基于传播学和社会学理论提出的，理论认为网络影响力节点度量从某种意义上是一个信息传播的系统，强调信息传播的有效性。本文基于传播学和社会学理论，采用k-shell来寻找核心层的节点，结合信息熵冗余度来剔除核心层的冗余节点，构建基于k-shell和信息熵冗余度的网络节点影响力度量模型。

2.2 k-shell算法

k-shell算法是一种剥洋葱式的网络结构分解算法，通过对节点的子图进行逐层分解，把极大子图称为k-cores（k-核）；而保留在极大子图中的节点存在的位置称为k-shell，节点的k-shell值是k-shell层中节点的重要特征。k-shell算法分解社会网络结构的步骤如下：

（1）去掉度数为1的网络节点，剩下一个子图，若该子图中仍然具有度数为1的节点则继续删除，直到该子图G1存在的节点度数都大于1，那么被删除的节点属于ks=1的核；

（2）与上一步类似，删除子图G1中度数为2的节点，直到该子图G2中存在的节点数都大于2，那么这一步被删除的节点属于ks=2的核；

（3）以此类推，逐步增加k值，对节点的子图进行逐层分解，直到所有节点被划分到k-shell中，而这些节点所在的子图被称为极大子图。

首先获取一个网络节点连接图，如图1所示；将网络节点中度数为1的节点以及边去掉，剩下一个子图，若该子图中仍然具有度数为1的节点则继续删除，那么所有被删除的节点被纳入于ks=1的核，如图2所示。

采取同样的方法把相应的节点划分到ks=2的核中，如图3所示。

重复上述步骤，直到所有的节点被去除。如图4所示，相应的网络节点被划分到ks=3的核中。网络结构分解结束后，每个节点均有一个ks值。很显然，采用k-shell值反映节点在网络中的核心位置是有问题的，因为所处核心层的所有节点的信息传播特征是有差异的。研究表明[9]，某些节点具有较高的信息熵冗余度，这类节点在信息传播过程中的重要性明显低于具有较低的信息熵冗余度的节点。因此，本文在k-shell算法的基础上，结合网络节点信息熵冗余度来识别真正的核心节点。

图1 网络节点连接图

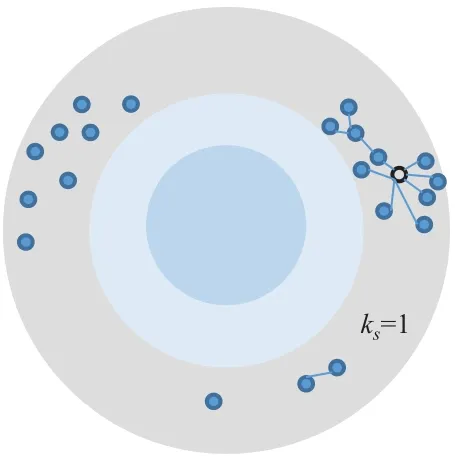
图2 ks=1的核所包含的节点

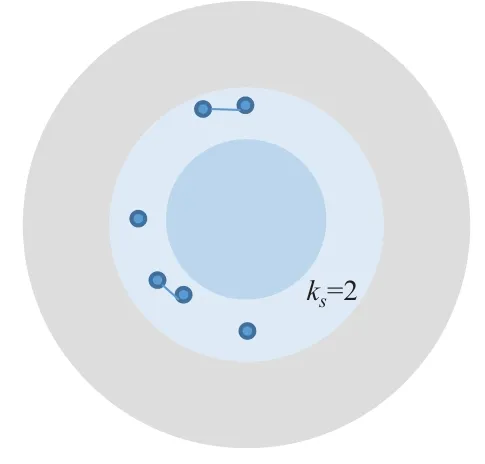
图3 ks=2的核所包含的节点

图4 ks=3的核所包含的节点

2.3 网络节点信息熵及其冗余度

熵是对系统不确定性的度量[11]。在信息论中，根据香农定义的信息熵是指信息的数学期望。根据这个概念，研究者把熵理解为某种特定信息出现的概率。而从熵这个概念引申出来了系统的有序化程度：一个系统越有序，其信息熵就越低。在社会网络中，节点的信息传播需要衡量两个方面：信息传播的可达率以及准确率。

可达率是指信息在两个节点中流动，设从起始节点出发到终止节点的时间跨度为As，从节点i传播到其相邻节点的时间跨度为li，则节点i的信息传播可达率为：

同理，根据网络的拓扑特性，信息从一个节点传播到另一个节点需要跨越节点的总数量为Az，与节点i直接关联的节点数量为ki，则节点i的信息传播准确率为：

那么，节点i的综合信息熵为：

其中：

根据冗余度的定义，节点i的信息熵冗余度为：

节点信息熵冗余度对网络节点中心性的计算、社区划分、网络控制、网络传播路径的识别等基于网络的应用有显著影响，这一研究结果对于认识复杂网络的拓扑结构、准确区分网络节点角色有着重要意义。

节点影响力度量的方法为：考虑节点的ks值，在ks值相同的情况下，结合公式(5)所得的熵冗余度对节点的影响力进行综合排名，熵冗余度越大表示节点的排名越后。

3 基于k-shell和信息熵冗余度的网络节点影响力度量流程

本文基于k-shell和信息熵冗余度的网络节点影响力度量流程具体如下：

（1）获取某地市运营商最近一个月的部分移动用户的移动社交数据；

（2）基于上述数据，构建移动用户的社交网络；

（3）采用k-shell的方法分解网络结构，得到核心层的移动用户；

（4）结合信息熵冗余度判断核心层存在的冗余节点；

（5）通过实验的方法验证利用信息熵冗余度算法是否能够识别存在传播影响力较大的核心层节点，采用实验对比的方法来判断本文提出的算法是否能够提高具有较高传播影响力的核心用户选取的精度。

3.1 获取源数据，并对数据进行清洗

本文以某运营商一个月1 860名移动用户的通话记录为例，如果某个用户在一个月中与另一个用户发生联系，那么可以认为这两个节点之间具有连通性。用户通话数据具体如表1所示：

表1 用户通话数据

根据上述通话数据，下一步的工作就是对数据进行清理，比如一些公共电话（快递电话、中介电话等）。因此，本文采用TF-IDF算法来清理通信用户数据，相关的方法[12]不再赘述。

3.2 构建通信用户社交网络图

根据清洗后的移动用户数据，构建移动用户的通信网络图，其矩阵的表示方式如表2所示。

3.3 采用k-shell的方法分解网络结构

采用k-shell的方法分解网络结构，得到核心层的用户如表3所示。

从表3可知，基于k-shell的方法分解网络结构可获得13层用户数据，其中第13层是网络的核心层，拥有8个核心节点。为验证本文提出算法的有效性和可行性，分别对仅使用k-shell算法寻找核心节点以及k-shell结合信息熵冗余度的方法寻找核心节点这两种方法进行了8组实验。在试验之前，本文把上述核心层的8个用户号码进行编码，分别是1～8，得到的相关信息具体如表4所示：

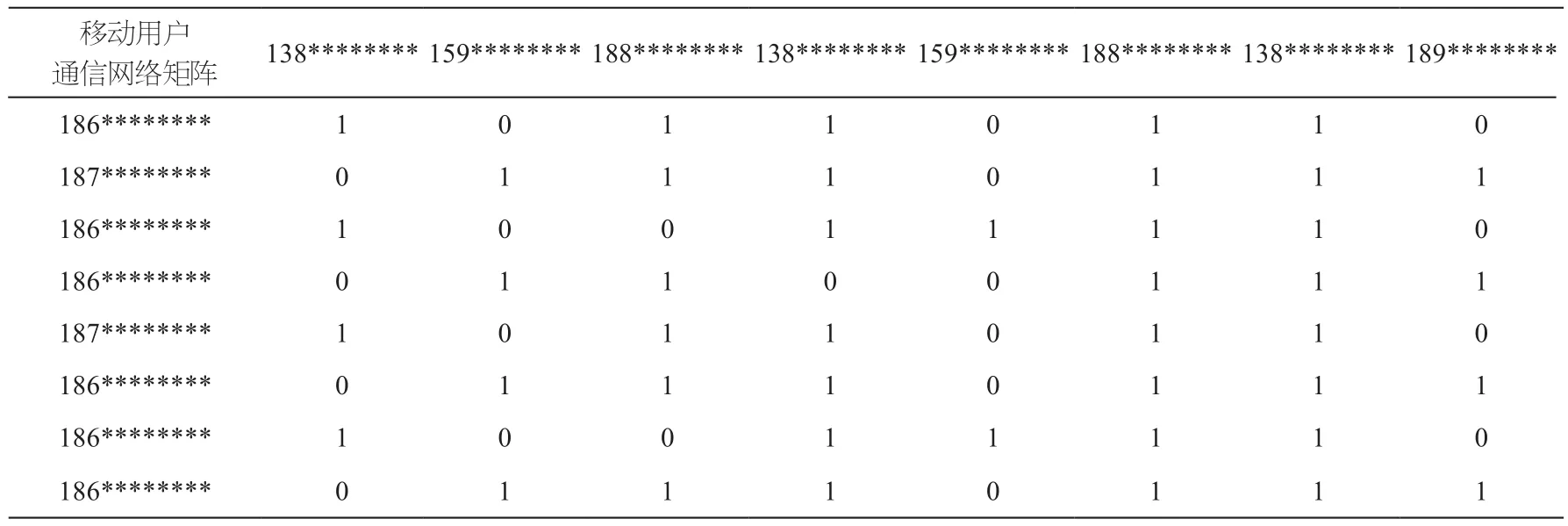
表2 移动用户通信网络矩阵

表3 基于k-shell算法进行网络结构分解

表4 各节点的相关信息

在本次试验中，设信息传播率为0.2。本次试验采用标准的SIR模型来模拟影响力的传播。

首先，采用经典的k-shell得出核心点后，随机选取节点1～8中的2个节点、4个节点、6个节点以及8个节点进行信息传播，得到整个网络中信息被有效、真实传播的节点数量；然后采用本文提出的方法得到核心层的8个节点，计算各个节点信息熵冗余度并将其进行排序，分别选取排名前2名的节点、前4名的节点、前6名的节点以及前8名的节点进行信息传播，得到整个网络中信息被有效、真实传播的节点数量。相关的对比结果如表5所示：

表5 经典的k-shell算法与本文算法的传播节点数量对比

在真实网络中，网络各层连接具有多样性的特点，节点本身具有信息熵，且较低熵值的节点所携带的信息量较少，其传播给相邻节点的影响力也较小。本文通过提取信息熵冗余度的方法，并采用实验对比了上述两组数据的连接特征，确定节点的潜在影响力在信息传播中的重要性。实验发现，有一类节点存在于网络连接的核心层，但本身具有较高的信息熵冗余度。也就是说，虽然节点本身拥有较高的连接数量，但其携带的信息量较少，对周围的节点具有较低的影响力，影响周围其他节点的数量有限。从表5可知，采用经典的k-shell算法的传播节点数量比本文算法的传播节点数量少，实验结果证实了网络核心层确实存在具有较高信息熵冗余度的节点，这类节点往往具有较低的传播性。因此，在选择核心节点时，通过过滤具有较高信息熵冗余度的节点能够在很大程度上提升核心节点选取的精度以及信息传播的准确性。这一结果对于运营商实施产品的推广以及病毒营销具有重要的意义。

4 结束语

本文提出基于k-shell和信息熵冗余度的网络节点影响力度量算法，即通过k-shell算法来提取核心层的节点，采用信息熵冗余度来过滤具有较高信息熵冗余度的节点，综合上述两种算法来选择网络中具有影响力的节点。本文的算法能够有效识别存在网络核心层但由于自身携带的信息量较少，对周边具有较低影响力的节点，使得保留下来的节点不仅具有较高的连接数量，而且本身具有较高的传播影响力，从而提升核心节点对网络的传播影响力，有效地解决了k-shell指标度量的核心层节点并不能真实反映其在网络传播影响力中的核心位置这一问题，合理地规避了核心层节点选取的随意性较高的问题，实现了基于k-shell指标选取的核心节点的客观化和科学化。由于本文仅针对某运营商的部分移动用户数据进行研究，因此适用性和扩展性有限。后续可针对移动运营商某个省的用户数据进行研究，以扩展该算法的适用范围。

[1] Ellison N B. Social network sites: Definition, history,and scholarship[J]. Journal of Computer-Mediated Communication, 2007,13(1): 210-230.

[2] 任晓龙,吕琳媛. 网络重要节点排序方法综述[J]. 科学通报, 2014(13): 1175-1197.

[3] 任卓明,邵凤,刘建国,等. 基于度与集聚系数的网络节点重要性度量方法研究[J]. 物理学报, 2013,62(12): 522-526.

[4] Chen D, Lu L, Shang M S, et al. Identifying influential nodes in complex networks[J]. Physica A Statistical Mechanics & Its Applications, 2012,391(4): 1777-1787.

[5] Gao S, Ma J, Chen Z, et al. Ranking the Spreading ability of nodes in complex networks based on local structure[J].Physica A Statistical Mechanics & Its Applications,2014,403(6): 130-147.

[6] Freeman L C. Centrality in social networks conceptual clariベcation[J]. Social Networks, 1978,1(3): 215-239.

[7] Kitsak M, Gallos L K, Havlin S, et al. Identification of influential spreaders in complex networks[J]. Nature Physics, 2011,6(11): 888-893.

[8] Bae J, Kim S. Identifying and ranking inぼuential spreaders in complex networks by neighborhood coreness[J].Physica A Statistical Mechanics & Its Applications,2014,395(4): 549-559.

[9] Liu Y, Tang M, Zhou T, et al. Core-like groups result in invalidation of identifying super-spreader by k-shell decomposition[J]. Scientiベc Reports, 2015(5): 9602.

[10] Lü L, Zhang Y C, Yeung C H, et al. Leaders in social networks, the Delicious case[J]. Plos One, 2011,6(6):1-9.

[11] 王俊,杜翠凤. 基于熵理论的ERP业务流程评价体系研究[J]. 移动通信, 2016,40(16): 20-24.

[12] 蒋仕宝,陈少权. 基于呼叫指纹的重入网识别算法研究[J]. 移动通信, 2016,40(22): 27-30.

[13] Silva R A P D, Viana M P, Costa L D F. Predicting epidemic outbreak from individual features of the spreaders[J]. Journal of Statistical Mechanics Theory&Experiment, 2012(7): 1-8.★