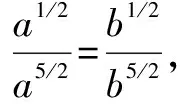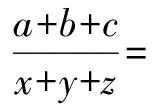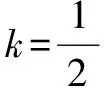柯西不等式及其在高考中的应用

韩 芳

(宁夏银川市实验中学 750001)

一、二维形式的柯西不等式形式及其证明

设a,b,c,d∈R，则(a2+b2)(c2+d2)≥(ac+bd)2，当且仅当ad=bc时，取等号.

证法一(配方法)(a2+b2)(c2+d2)=a2c2+a2d2+b2c2+b2d2

=(ac+bd)2+(ad-bc)2≥(ac+bd)2.

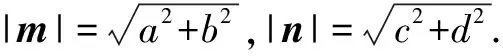
∵m·n=ac+bd，且m·n=|m||n|cos〈m,n〉，则|m·n|≤|m||n|.

∴ (a2+b2)(c2+d2)≥(ac+bd)2.

证法三(构造二次函数法)设f(x)=(a2+b2)x2-2(ac+bd)x+c2+d2，

∵f(x)=(ax-c)2+(bx-d)2≥0恒成立.

∴Δ=[-2(ac+bd)]2-4(a2+b2)(c2+d2)≤0，即(a2+b2)(c2+d2)≥(ac+bd)2.

二、一般形式的柯西不等式及其证明

设a1,a2,…,an,b1,b2,…,bn∈R,则

当且仅当bi=0(i=1,2,…,n)或∃k∈R,ai=kbi(i=1,2,…,n)时,取等号.

三、柯西不等式在高考中的应用

结合全国各省不等式选讲这一模块的选做题，我们发现，陕西、福建、湖北等地考查柯西不等式的居多，而借助柯西不等式解题的难点在于要能把原问题变为适合于柯西不等式的各种形式，这就需要抓住应用柯西不等式的两个主要技巧：一是在于构造两组数；二是结合题目中的数值特征，来拆分柯西不等式中的常数.

1.求函数的最值

例1 (2015·福建卷)已知a>0,b>0,c>0,函数f(x)=|x+a|+|x-b|+c的最小值为4.

(1)求a+b+c的值；

解析(1)因|x+a|+|x-b|+c≥|(x+a)

-(x-b)|+c=a+b+c，当且仅当-a≤x≤b时，等号成立.因为f(x)的最小值是4，所以a+b+c=4.

(2)由(1)知a+b+c=4，由柯西不等式得

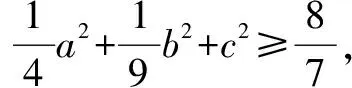
点评在解题中，要想使用柯西不等式，就得先理解它的数学意义和外在形式，当一个代数式与柯西不等式的左边或右边形式一致时，可考虑利用柯西不等式对这个式子放缩.

例2 (2015年高考数学陕西卷，24)已知关于x的不等式|x+a|

(1)求实数a，b的值；

解析(1)解得a=-3，b=1.

点评作为一种非常重要的解题工具—柯西不等式，其在应用求解相关不等式时,关键在于构造出柯西不等式的形式，并注意能取到等号的条件.

2.证明不等式

例3 (2014·浙江卷)设正数a,b,c满足abc=a+b+c，求证：ab+4bc+9ac≥36，并给出等号成立条件．

∴ab+4bc+9ac≥36，当且仅当a=2,b=3,c=1时,取等号.

例4 (2017年新课标Ⅱ卷，第23题)已知a>0,b>0,a3+b3=2,证明：(1)(a+b)(a5+b5)≥4;(2)a+b≤2.

解析(1)由柯西不等式得

3.证明等式与解方程

4.在解析几何中的应用

例6 (2008年高考新课标卷Ⅱ理科21题)设椭圆中心在坐标原点，A(2，0)，B(0，1)是它的两个顶点，直线y=kx(k>0)与AB相交于点D，与椭圆相交于E、F两点．

(Ⅱ)求四边形AEBF面积的最大值．

灵活巧妙地应用柯西不等式，可以使得一些较为复杂的数学问题简单化.通过以上几个方面的应用举例，使我们不仅掌握了柯西不等式在数学解题中的应用技巧，而且了解了高考对柯西不等式知识的考查程度，从而，使我们更加科学和高效地对相关问题进行系统化的复习.

[1] 华东师范大学数学系．数学分析(第三版) [M]．北京：高等教育出版社，2001．

[2]中学数学课程教材研究开发中心.普通高中课程标准实验教科书(数学选修4-5)[M].北京：人民教育出版社，2007.

[3]杨丽英.柯西不等式的证明及应用[J].内蒙古师范大学学报(自然科学版),2013,42(1):16-20.