混响背景下GTM回波检测算法研究

刘启军，张雪松，王易川，张宗堂

(1. 海军潜艇学院，山东青岛 266199；2. 吉林省航道管理局，吉林吉林 132013)

0 引 言

对于主动声呐，在浅海环境中，其背景噪声主要为混响而非海洋环境噪声。混响是大量的散射波叠加形成的[1]，它在时域上和回波信号有很强的相关性且在频域上频谱有重叠，因此单纯从时域或频域很难从混响中检测出回波信号。

匹配滤波器是平稳高斯白噪声条件下的最佳检测器[2]。不同于一般海洋环境噪声，混响具有非平稳性、有色性、非高斯性等特性，这使得在混响背景下使用匹配滤波器受到了严重的限制。一种可行的解决办法是对混响背景进行处理，使其接近平稳高斯白噪声。文献[3-5]利用多种方法对混响进行预白化处理，改善其有色性。文献[6-7]认为混响服从局部平稳条件，再利用平稳信号处理方法分析。文献[8-10]则考虑了混响的非高斯性。本文统筹考虑混响的非平稳性、有色性和非高斯性，在此基础上建立了混合高斯时变自回归模型和混响特性评价方法，实现了回波检测和滤波效果评价。

1 混合高斯时变自回归模型(GTM)

激励un是高斯白噪声。虽然这种模型适应于大部分情况，但在有些时候则会失效，例如在水下利用主动声呐进行探测和识别时，混响中往往会有突出的冲激，其概率密度函数是具有重尾特性的非高斯分布。

为了解决上述问题，对AR模型进行改进。设激励un服从混合高斯分布，即：

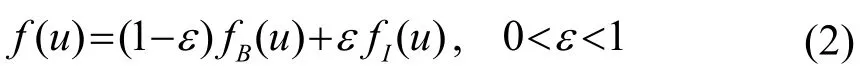
混合高斯自回归模型可以对有色非高斯数据进行建模，分别估计出其功率谱密度和概率密度。但它是在信号平稳的框架下进行参数估计的，而混响信号往往是非平稳的。时变自回归(Time-Varying Autoregressive，TVAR)模型的参数是随时间变化的，可以通过估计混响的时变功率谱来刻画其有色性。因此用TVAR模型取代AR模型，再结合混合高斯模型，提出了 GTM。从而综合考虑了混响的非平稳性、有色性和非高斯性。

基函数算法是T.S.Rao[12]提出的一种算法，它将参数看做一些函数的加权和，如果利用2阶多项式来对参数进行展开，即：

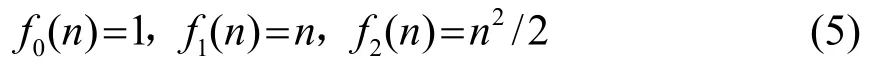
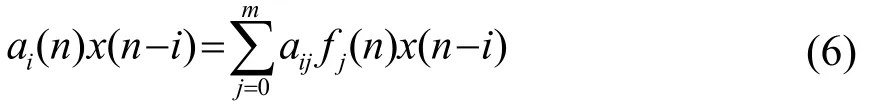
定义矢量：

式(3)可以表示为：

将递推最小二乘算法推广到时变参数模型中，则

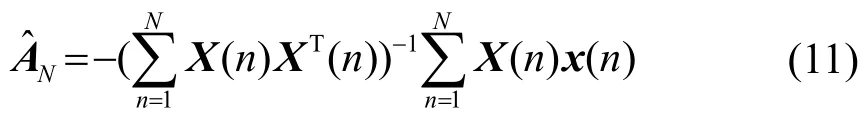
令

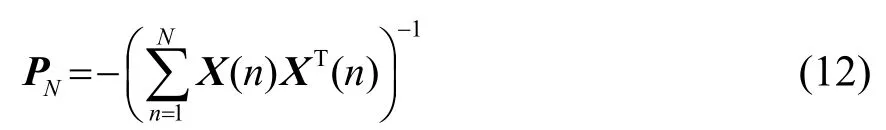
则有如下递推算法：

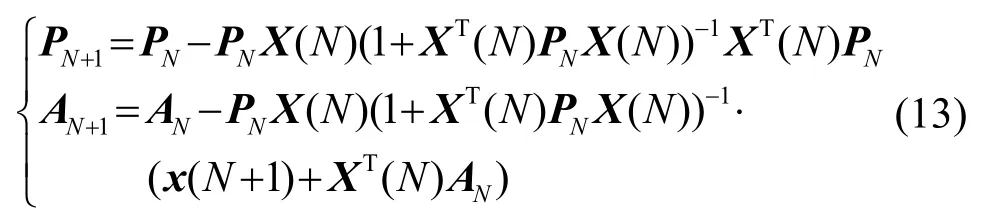
对于p阶模型，递推从第p+1点开始，初值选取如下：

式中：I1为P(m+1)阶单位列向量，I2为P(m+1)×P(m+ 1)单位矩阵。 取一个较小的数而Ψ取一个较大的数。如果把混响噪声和环境噪声统一看作混响，则混响背景下的回波信号检测问题可以由二元检测问题描述，即当接收信号中无回波信号时，接受假设H0，当接收信号中有回波信号时，接受假设H1，如式(15)所示。

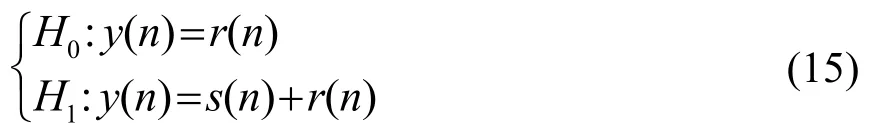
式中，y(n)为接收信号，r(n)为混响信号，s(n)为回波信号。

对于主动声呐信号检测问题，最典型的方法是匹配滤波法，它是在平稳高斯白噪声背景下的最佳检测器。然而混响背景往往是非平稳、有色、非高斯的。如果继续使用匹配滤波器在混响干扰下检测回波信号，则需要对混响进行白化处理和高斯化处理，使其尽量满足平稳高斯白噪声的条件，然后再进行匹配滤波。本文采用的白化和高斯化处理方法是在混响的GTM模型下，通过对混响的功率谱密度(Power Spectral Density，PSD)函数和PDF估计，构建白化滤波器和高斯化滤波器组成 GTM 滤波器，从而形成GTM回波检测算法。

白化滤波器是利用时变系数构造传输函数：

式中，ak(z)为时变系数。

将混响r(n)通过上述白化滤波器可以得到白化后的新序列r'(n)：

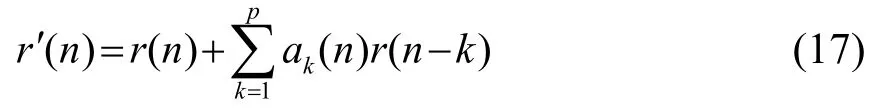
高斯化滤波采用的是U滤波，即先通过GTM估计其PDF，然后构建U函数[13]：

式中：f为概率密度函数；f'为其一阶导数。因此有如图1所示的GTM回波检测。

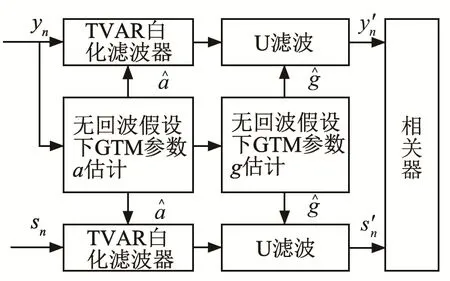
图1 GTM回波检测流程图Fig.1 The flow chart of GTM echo detection

2 混响特性评价方法

如果上述检测方法效果不佳，单纯从相关器输出无法判断是接收信号本身的相关性较弱，还是滤波的效果不佳。另外从滤波的角度来看，也无法知道是哪一个滤波器环节出了问题。为此，本文提出一种定量衡量混响特性及滤波效果的评价方法。该方法包含非平稳度、有色度和非高斯度三个评价标准，分别对混响的非平稳性、有色性、非高斯性进行定量描述。

文献[14]中提出用Itakura距离定量描述序列非平稳性。应用Itakura距离时，首先需要对信号进行分段，然后计算相邻两段的Itakura距离，因此一个被分为n段的信号会有n−1 段Itakura距离。为了更直观地比较两个信号的非平稳性强弱，把一个信号全部Itakura距离的平均值定义为非平稳度P，用来量化信号非平稳性的大小，即：

由于白噪声是功率谱密度为常数的噪声，所以当功率谱密度的波动越大时，噪声的有色性就越强。而方差是描述随机变量与其期望偏离程度的统计量。如果用方差的概念来刻画有色性的大小，便可定义混响的有色度C的概念，即混响功率谱密度的方差：

当信号为白噪声时，其有色度为 0。信号的有色性越强，则其有色度越大。

随机变量X的偏度βs是其分布偏斜方向和程度的度量，而峰度βk表示PDF在平均值处峰值的高低。若则定义非高斯度G为：

当序列服从高斯分布，则其非高斯度G0=0。G的值越大，说明序列的非高斯性越强。

从非平稳度、有色度和非高斯度的定义可以看出，若混响的三个评价标准的数值越小，则说明混响越接近于平稳高斯白噪声的理性条件。这里便蕴含了一个“相对性”的概念，即单独一段混响特性的“绝对数值”是无参考性的，而将它与经过滤波处理后的混响的特性相比较，其数值的相对大小便可以作用对滤波器进行评价的依据。经过滤波处理后，若混响的非平稳度降低，则滤波器可以改善混响的非平稳性；若有色度降低，则滤波器可以改善混响的有色性；若非高斯度降低，则滤波器可以改善混响的非高斯性。

3 模型验证

利用AR模型和TVAR模型对实测混响的功率谱密度进行建模。其中TVAR模型的参数运用基函数法进行估计，基函数采用二阶多项式基函数。取AR模型的模型参数分别为5、10、50，依次得到如图2～4所示的结果。

从图中可以看出，TVAR模型能够较好地拟合混响的功率谱密度。而低阶数的AR模型与真实的混响模型的功率谱密度相差较大，随着阶数的增大，其拟合精度不断提高，当阶数为 50时可以较好地拟合混响的功率谱密度。但实际工作中，模型阶数一般未知，如果想要利用AR模型达到较好地拟合效果，则需要运用定阶准则来对阶数进行估计。增加了算法的复杂性。同时，最优定阶准则的选取也是一个复杂的工作。因此，TVAR模型不但拟合效果理想，而且实际运用时更加简练可行。

图2 AR模型与TVAR模型的功率谱密度 (AR阶数为5)Fig.2 The PSDs of AR and TVAR models (the order of AR is 5)

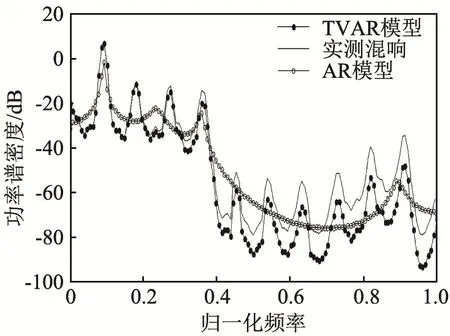
图3 AR模型与TVAR模型的功率谱密度 (AR阶数为10)Fig.3 The PSDs of AR and TVAR models (the order of AR is 10)

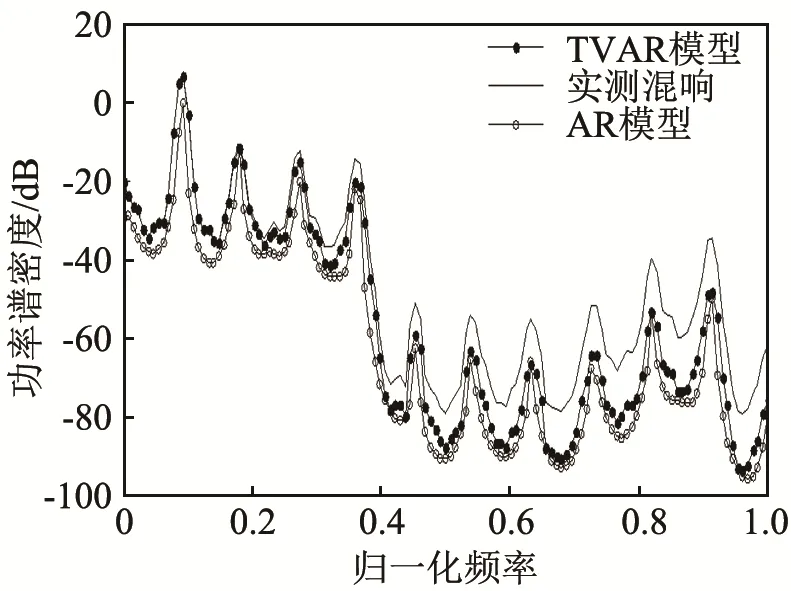
图4 AR模型与TVAR模型的功率谱密度 (AR阶数为50)Fig.4 The PSDs of AR and TVAR models (the order of AR is 50)

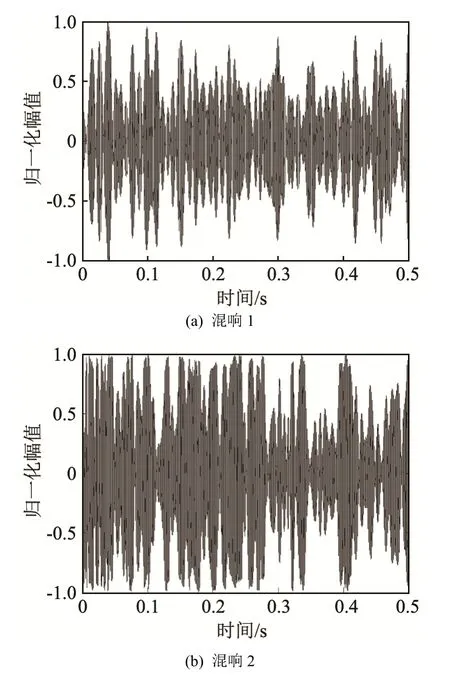
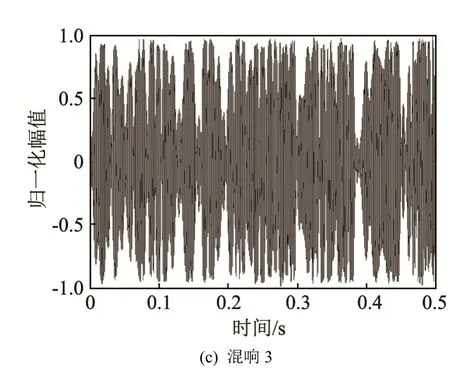
图5 实测混响时域波形Fig.5 The waveform of measured reverberation

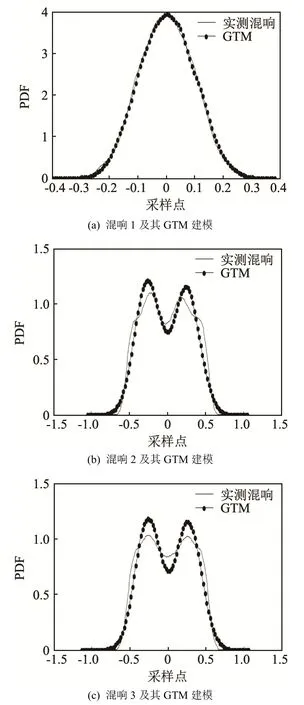
图6 实测混响与GTM建模的概率密度Fig.6 The PDFs of measured reverberation and GTM modeling

利用三段海上实测混响对上文建立的GTM进行模型验证，模型验证之前先对原始数据做去均值处理。图5为混响时域波形，图6和图7分别是其概率密度曲线和功率谱密度曲线。从图6中可以看出，对于服从高斯分布(图 6(a))和非高斯分布的混响，GTM 均能较好地拟合其概率密度。同时图 7表明GTM对功率谱密度也能够达到较好的拟合效果，从而验证了模型的有效性。

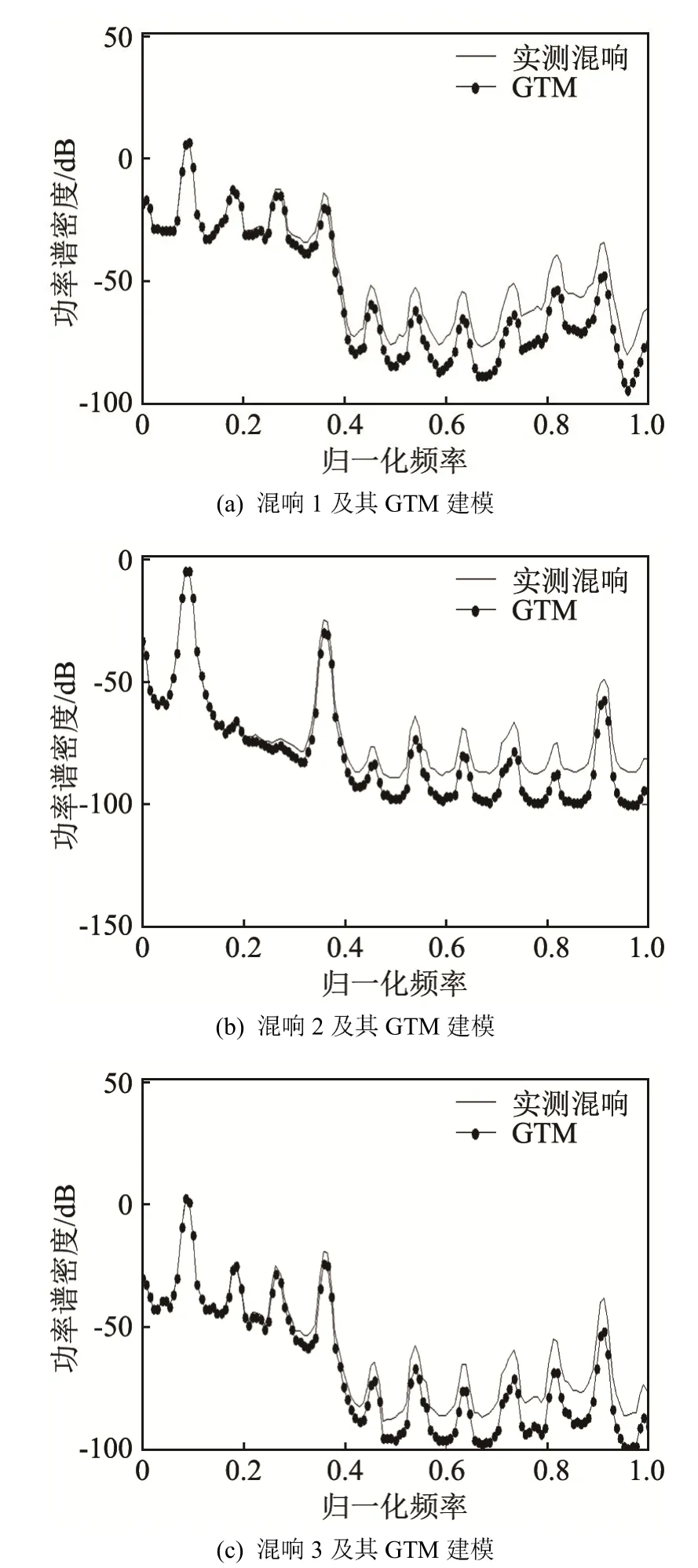
图7 实测混响与GTM建模的功率谱密度Fig.7 The PSDs of measured reverberation and GTM modeling

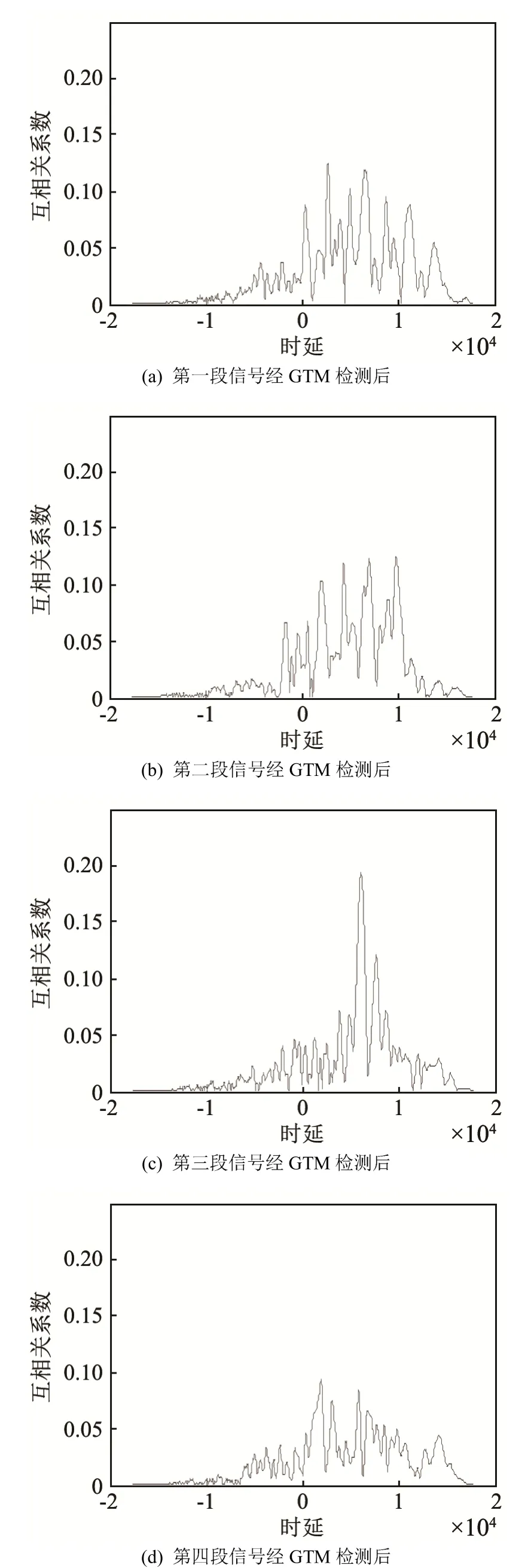
图8 每段信号经GTM检测后的互相关系数Fig.8 Cross correlation coefficient of each signal section after GTM detection

4 实测信号分析

根据上文构建的GTM回波检测算法对实测混响信号进行检测。将信号分为四段，分别作 GTM回波检测，得到各段的相关器输出，如图8所示。从图8(c)可以看出明显的互相关峰，峰值为0.19，在设定适当的检测门限后能够检测出回波信号。而对第三段信号进行普通预白化检测得到图9，其峰值为0.16，说明GTM检测算法优于普通预白化检测算法。

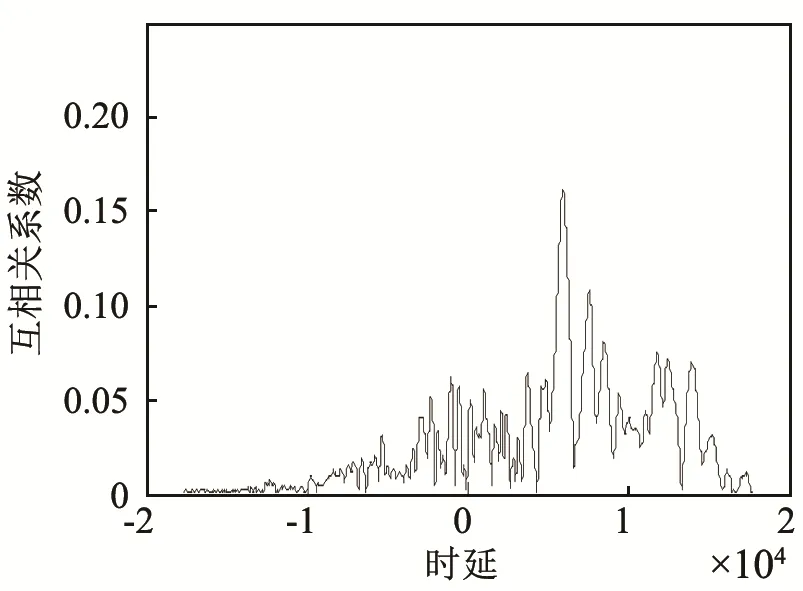
图9 第三段信号经普通预白化检测后的互相关系数Fig.9 Cross correlation coefficient of the 3rd signal section after prewhitening detection

运用混响特性评价方法对该段(第三段)信号进行评价。分别计算出未经滤波和经过GTM滤波的混响的非平稳度、有色度和非高斯度如表1所示，滤波后，混响的非平稳度由0.132 5降低到0.044 6，即提高了平稳性；有色度由 16.079 6降低到15.099 4，说明滤波后混响更接近于白噪声；非高斯度由1.527 9降低到0.776 4，即滤波后混响更接近于高斯噪声。可以看出GTM滤波可以改善混响的特性。

表1 滤波前后混响特性比较Table 1 Reverberation features before and after filtering

为了验证GTM滤波方法的有效性，对全部32个实测混响信号进行处理，取其检测出回波的那段信号，分别进行评价，得到其非平稳度、有色度和非高斯度的平均值和优化率如表2所示，其中优化率指滤波后混响特性得到改善的信号数量占总数量的比例。

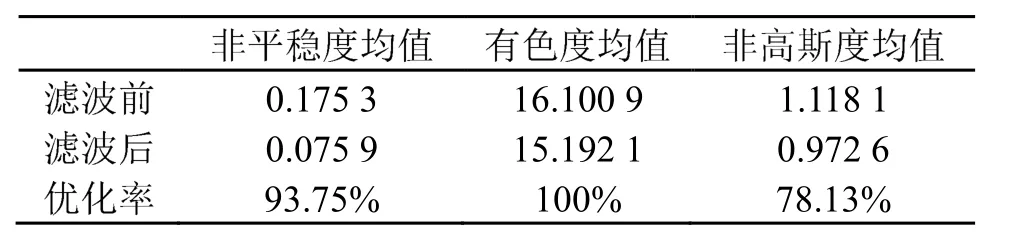
表2 滤波前后混响特性统计结果(对32个实测混响信号)Table 2 Statistical results of reverberation features before and afterfiltering for 32 measured reverberation signals

5 结 论

经过模型验证，本文提出的GTM可以较好地拟合实际混响的概率密度与功率谱密度。结合实测信号分析，GTM 回波检测算法实现了回波信号的有效检测且效果优于普通预白化检测算法。利用提出的混响特性评价方法得到的统计结果可以看出，经滤波后的混响特性亦得到了改善，证明了算法的工程应用价值。

[1]刘伯胜, 雷家煜. 水声学原理[M]. 哈尔滨: 哈尔滨工程大学出版社, 2011, 7: 200.

LIU Bosheng, LEI Jiayu. Underwater acoustics principle[M]. Harbin: Harbin Engineering University Press, 2011, 7: 200.

[2]Van Trees H L. Detection, Estimation, and Modulation Theory-Part 1[J]. John Wiley and Sons, 1968, Chapter 4.

[3]陈鹏, 侯朝焕, 马晓川. LFM 信号基于自适应预白化处理的GLRT检测器[J]. 系统工程与电子技术, 2006, 28(8): 1138-1140.

CHEN Peng, HOU Chaohuan, MA Xiaochuan. GLRT detection of LFM signal based on adaptive prewhitening[J]. System Engineering and Electronics, 2006, 28(8): 1138-1140.

[4]王汝夯, 黄建国, 张群飞. 基于分数阶傅里叶变换的LFM混响空时预白化方法[J]. 系统工程与电子技术, 2011, 33(7): 1523-1526.

WANG Ruben, HUANG Jianguo, ZHANG Qunfei. LFM reverberation space-time prewhitening based on FRFT[J]. System Engineering and Electronics, 2011, 33(7): 1523-1526.

[5]许江湖, 张明敏. 一种基于PCI技术预白的水下目标检测方法[J].信号处理, 2007, 23(1): 127-131.

XU Jianghu, ZHANG Mingmin. A underwater target detection method based on PCI prewhitening[J]. Signal Processing, 2007,23(1): 127-131.

[6]Steven Kay, John Salisburg. Improved active sonar detection using autoregressive prewhiteners[J]. J. Acoust. Soc. Am., 1990, 87(4):1603-1611.

[7]Carmillet V, Amblard P O, Jourdain G.Detection of phase-or frequency-modulated signals in reverberation noise[J]. J. Acoust. Soc.Am., 1999, 105(6): 3375-3389.

[8]孙文俊, 马远良, 杨益新. 非瑞利混响背景下接收机工作特性曲线仿真[J]. 声学与电子工程, 2007(85): 11-14.

SUN Wenjun, MA Yuanliang, YANG Yixin. Receiver working characteristics curve simulation under non-rayleigh background[J].Acoustic and Electronic Engineering, 2007(85): 11-14.

[9]Abraham D, Lyons A P. Exponential scattering and K-distribution reverberation[J]. MST/IEEE Oeeans 2001. An Ocean Odyssey.Conference Proeeedings, 2001, 31(3): 1622-1628.

[10]Abraham D A. Broadband detection in K distribution reverberation[J]. 2002 IEEE Sensor Array and Multichannel Signal Processing Work shop Proceedings, 2002, 23(2): 53-57.

[11]Debasis Sengupta, Steven Kay. Efficient estimation of parameters for Non-Gaussian Autoregressive Processes[J]. IEEE Transactions on Acoustics, 1989, 37(6): 785-794.

[12]Rao T S. The Fitting of Non-Stationary Time-Series Models with Time Dependent Parameters[J]. J Royal Statist. Soc. Series B,1970, 32(2): 256-263.

[13]王平波, 蔡志明. 非高斯数据的高斯化滤波[J]. 声学与电子工程,2006(83): 26-30.

WANG Pingbo, CAI Zhiming. Gaussian filter of non- gaussian data[J]. Acoustic and Electronic Engineering, 2006(83): 26-30.

[14]Carmillet V, Amblard P O, Jourdain G. Detection of phase- or frequency-modulated signals in reverberation noise[J]. J. Acoust.Soc. Am., 1999, 105(6): 3375-3389.