车载行李架结构的有限元分析方法
2017-02-06唐振华武文超尚丽娜
唐振华,武文超,吴 磊,尚丽娜
(泛亚汽车技术中心有限公司,上海 201201)
引言
随着国内越来越多的家庭拥有了汽车,特别是SUV车型保有量的持续增加,自驾游正成为一种时尚。由于人们活动的地域范围在不断扩大,以及自由度的增加,需要携带的物品也越来越多。但是车内的空间毕竟有限,只能通过加装一些附属设备来增加汽车的运能,而简单实用的车顶行李架,因为可以在旅行途中承载大量物品,为汽车扩展出更大的“空间”,成为许多车主竞相选装的汽车部件。
当然,车载行李架作为一个车辆外饰功能件,其安全的重要性不言而喻。在行李架完成初期设计时,如果没有经过计算机有限元分析而直接开模制造行李架再进行试验,万一试验不通过可能需要更改设计,将会造成原有模具报废的损失,所以通常在行李架数据完成后会进行针对测试标准要求的有限元分析,通过不断改进分析中的不合格设计,最终冻结满足标准要求的设计数据,然后进行开模制造,这种开发方式是相对可靠和安全的。
1 有限元法基本思想
有限元法的基本思想是将一个实际的实体结构均分为有限个数和有限大小的单元组合体来进行研究。这些单元会在节点处带有连接,单元之间的载荷将通过节点进行传递。这种把连续体解耦为分散结构的过程称为离散化,也叫做单元划分。
离散后单元节点的设定、性质和数量应根据所要解决问题的属性、变形形态的需求和分析精度而决定,所以有限元分析法中的所有结构不是原来的物体结构,而是同材料的众多单元连结而成的相对离散状形体。用有限元分析方法计算获得的最终结论只能是相对近似的,如果划分单元的数量充足且较为合理,那么得出的最终结论就与实际情况越符合。
1.1 有限元建模和分析软件
随着各种新型计算机技术的卓越发展,其各类软件和硬件条件的相继改进,为有限元分析等数值理论分析方法在计算机中的应用提供了充足条件。目前,行业内能进行大型复杂实体结构的精准建模和有限元分析的软件越来越多。本文选用了Hypermesh和Nastran分别对某中型SUV行李架进行有限元建模和分析计算。
1.2 有限元建模和分析的一般流程
有限元建模和分析的一般流程如图1所示。
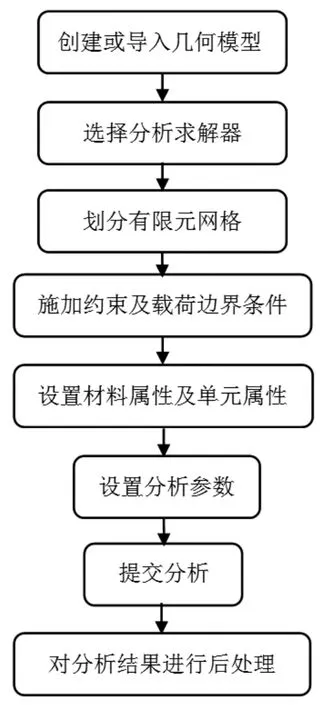
图1 有限元建模和分析的一般流程图
2 行李架的有限元分析方案及前期准备
2.1 行李架的分析方案
汽车行李架为梁结构,由于承载和行驶路况的不同,其载荷形式复杂多变。如果尝试选用经典力学方法来分析其刚度、强度或动态性能,就要求作大量简化或者假设,使得结果偏差加大;如采用实体试验进行演示,则需要利用各种手段制作样件,不仅费用高、时间长,而且很难实行相对全面地评估,复现影响结构各种性能的关键因素或环节将变得越来越难。计算机技术的不断发展和数值分析理论的逐渐优化,对汽车结构分析提供强有力地支持,传统车辆的设计开发由经验、对比、设计,转变为通过计算机辅助来建模并进行强度性能计算和分析优化。有限元分析技术能有效解决车辆车体设计开发过程中的模糊性,从而使车体及其部件结构的设计更加合理,降低了研发设计费用,减少了很多不必要的开支和时间。
本章主要就某中型SUV行李架的承载功能,采用Hypermesh和Nastran进行有限元建模分析。为了简化汽车行李架在各种复杂工况下的承载形式,根据企业子系统分析规范制定了11种具有代表性的受载形式,如表1所示,分别分析这11种工况下,该行李架的安全性能,此项目因定位问题,仅需完成等级1(50 Kg)的验证即可。
2.2 建模准备
2.2.1单位制及材料性能
大部分有限元分析计算程序不定义物理参数的单位,不同的单位可以被定义在不同条件下,但在同一个条件中各物理参数的单位必须保持一致。但是在现实车辆的工程设计问题中经常用到几种不同单位制的物理参数,若只是按照传统采用常用的单位,那这种定义单位方法是不一致的,将导致偏离的计算分析结果。
因此在有限元分析之前,首先要制定一套封闭的物理量单位制。由于在工程结构CAD建模中通常采用的是非国际单位制,如长度通常是毫米(mm),所以有限元分析通常也采用了一套工程单位制:毫米(mm)、吨(tone)、牛顿(N)、兆帕(MPa)等,它们也具有封闭性。表2提供了两套最常用的封闭单位制。本文中由于直接导入了CAE文件采用是工程单位制,因此,在前处理中,都采用工程单位制来进行处理。
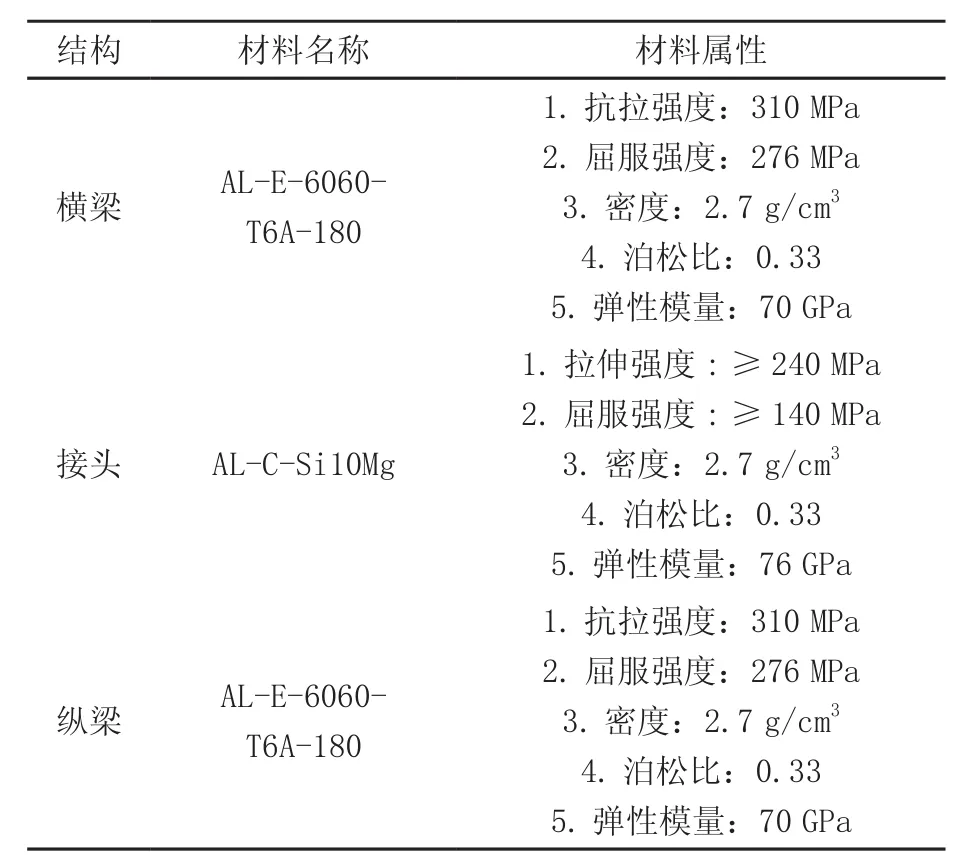
行李架的结构主要有纵梁、横梁、连接头以及其它相关配件,如图2。在有限元分析中,连接配件可忽略不计,只考虑整个系统的三个主体部件纵梁、横梁和连接头即可。纵梁、横梁和接头所选用的材料及其材料的力学属性如表3所示。
2.2.2模型简化
对于一些相对复杂的曲面造型,在操作方式上使用CAD造型软件相对于CAE软件要简单不少。本文采用了UGNX8.0软件进行了行李架的结构设计,产生了CAD文件,随后对该行李架进行有限元建模。
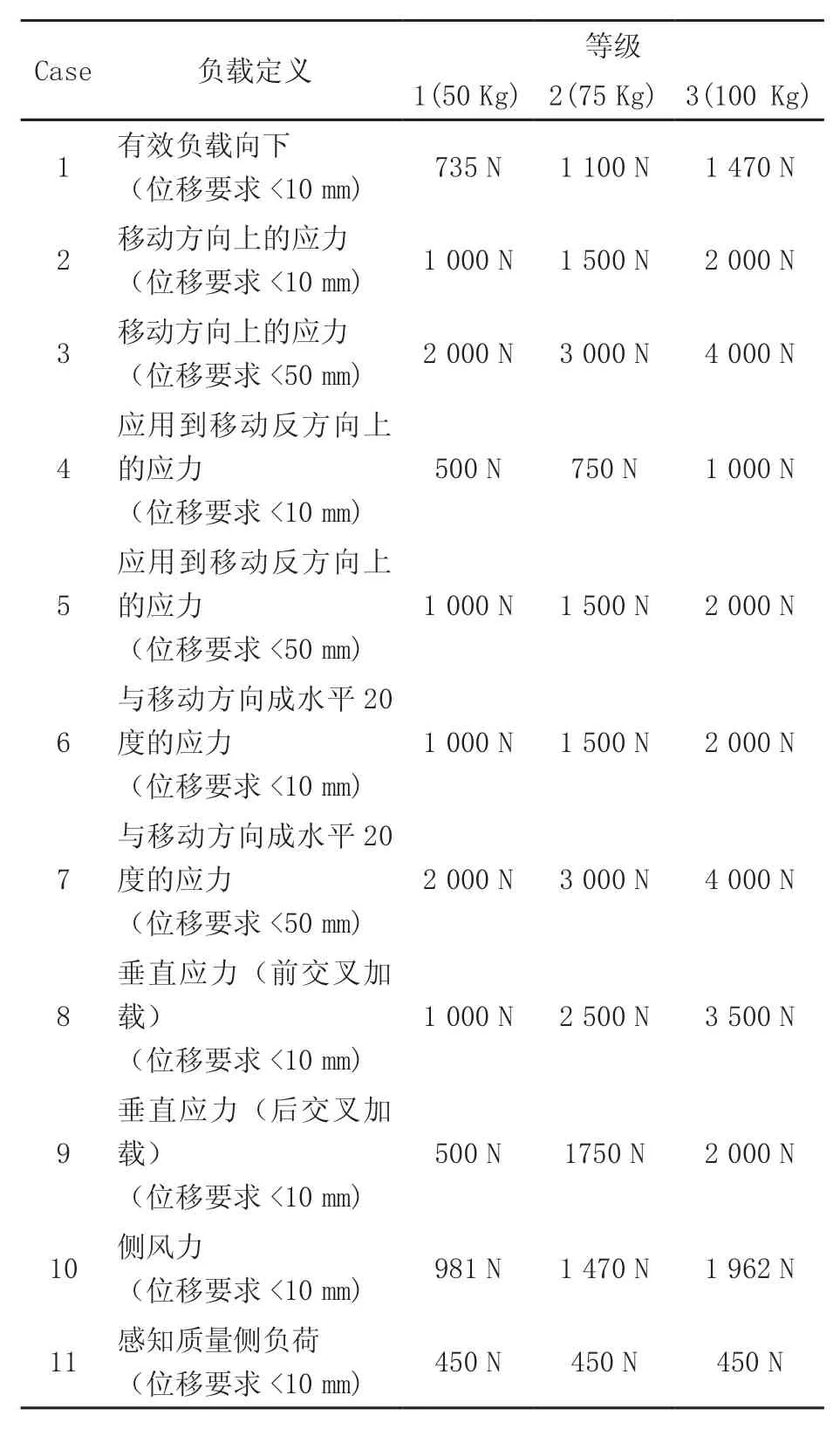
表1 11种工况负荷表
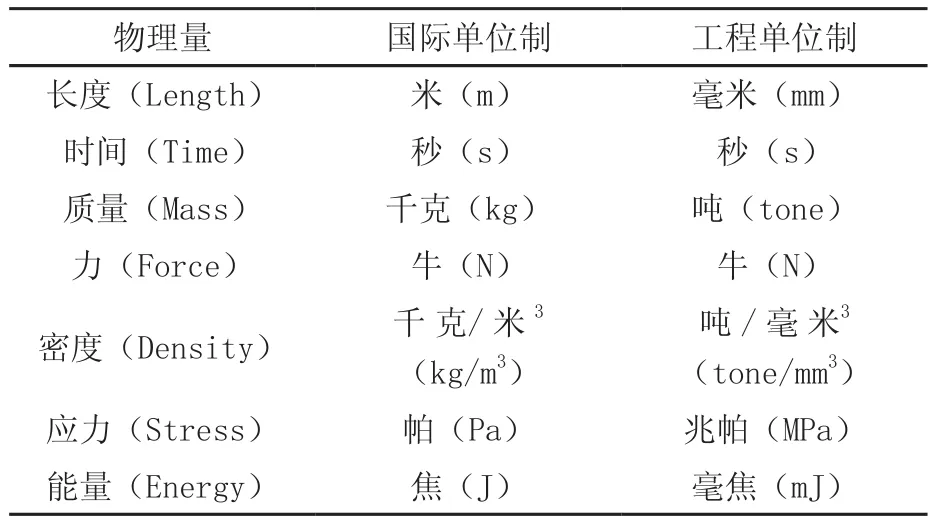
表2 有限元分析中两套常用单位制
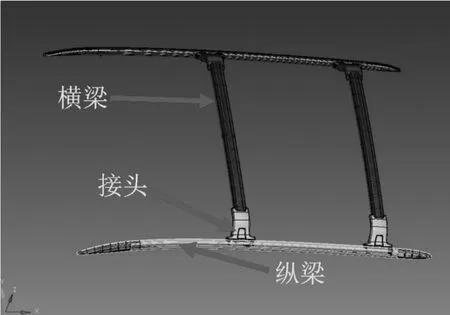
图2 某中型SUV行李架的结构组成
结构 材料名称 材料属性横梁 AL-E-6060-T6A-180 1.抗拉强度:310 MPa 2.屈服强度:276 MPa 3.密度:2.7 g/cm3 4.泊松比:0.33 5.弹性模量:70 GPa接头 AL-C-Si10Mg 1.拉伸强度:≥240 MPa 2.屈服强度:≥140 MPa 3.密度:2.7 g/cm3 4.泊松比:0.33 5.弹性模量:76 GPa纵梁 AL-E-6060-T6A-180 1.抗拉强度:310 MPa 2.屈服强度:276 MPa 3.密度:2.7 g/cm3 4.泊松比:0.33 5.弹性模量:70 GPa
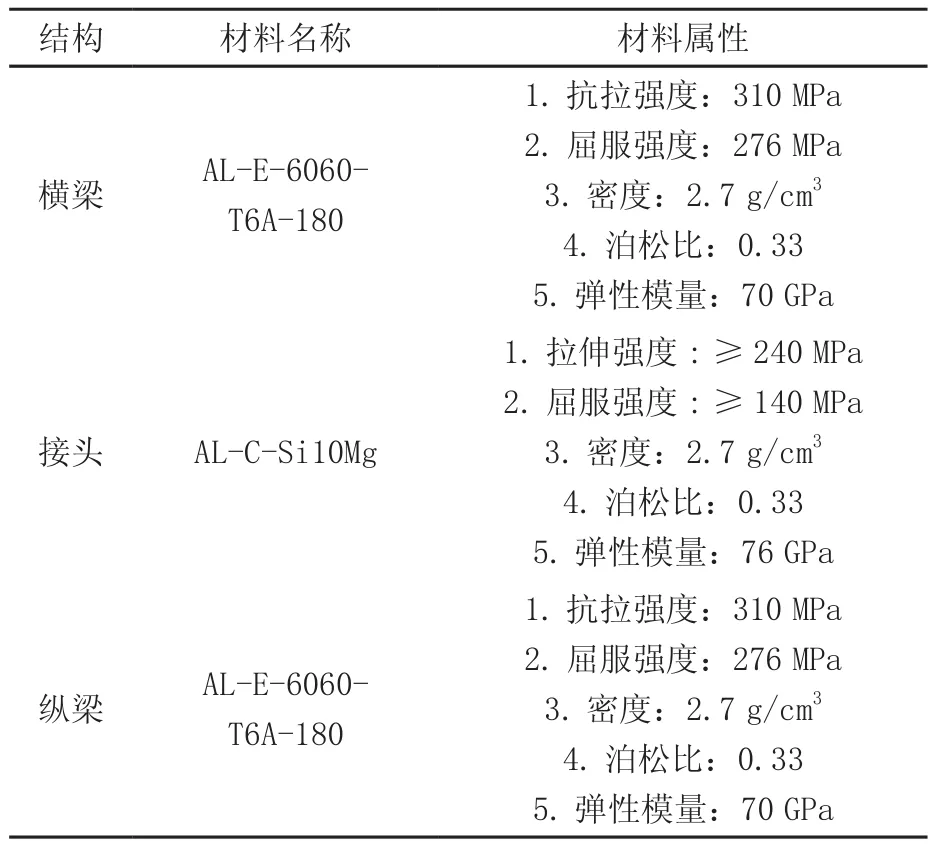
表3 某中型SUV行李架各个结构件的材料属性
汽车行李架除了纵梁、横梁和连接头主要承载部件外,还包括大量的承受应力的螺栓、垫片等连接配件和装饰配件。由于部分次要承载强度元件对于框架结构的形变和应力分布影响不大,但对解耦规模和最终结论准确性产生较大影响。所以不必参考车载行李架的实际设计结构来搭建有限元模型,可以通过各个部件分析的着重点对模型进行一些针对性简化。本文重点研究的是汽车行李架的承载安全性,因此根据实际需要建模时对行李架结构进行了简化。简化后只保留行李架的主体部分,如图3所示。
2.3 网格划分
如前章所述,有限元建模工作中网格的划分占有很重要的地位。通常来说网格的划分是有限元前处理过程中的主要关键工作。各元件网格划分的质量和优劣将对最终的计算分析结果带来较大影响。这项工作不仅繁琐、费时,而且在很多方面都依赖于操作人员的划分经验和技术。
2.3.1纵梁网格划分
纵梁在行李架的结构上主要起到连接横梁和汽车体的作用,属于承载部件,但是为了节省计算成本,采用壳单元在几何中面划分网格,平均尺寸6~8 mm,最小尺寸不小于2 mm。图4为纵梁结构的网格划分图。主要采用主体部分四边形单元,不规则的地方采用三角形单元的方法对横梁结构进行了网格划分。
2.3.2横梁网格划分
横梁为行李架的直接承载部件,为了得到较为精确的有限元分析结果,横梁采用六面体实体单元划分网格,平均尺寸2mm,最小尺寸不小于1mm。考虑到行李架本身的尺寸较大,过密的网格会急剧增加计算成本,因此在行李架横梁上截面采用单层网格进行建模,然后映射到整个长度上,如图5所示。
2.3.3连接头网格划分
两根横梁经四个接头分别连接到两条纵梁上,将横梁上载荷传递到纵梁上。由于结构和曲面比较复杂,因此适宜采用四面体网格进行划分。最方便的方法就是自由网格划分,采用四面体结构对接头构件进行有限元建模,平均尺寸5 mm,最小尺寸不小于2 mm。同时接头与承载构件横梁直接连接,因此网格的尺寸选择尽量与横梁网格相近,减小有限元计算的误差。接头的有限元网格划分如图6所示。

图3 某中型SUV行李架装配体模型简化

图4 行李架纵梁网格划分底部视图

图5 行李架横梁有限元网格划分断面图

图6 行李架接头有限元网格划分
图7为某中型SUV行李架主体结构有限元网格,该主体结构包括2条纵梁、2条横梁和4个连接头。有限元模型的总共网格数量为217 692个。
2.4 边界条件定义
边界条件通常是有限元分析中不可缺失的重要组成部分,边界条件可以在网格划分完成之后进行施加。,当有限元模型和几何模型相关联时,Hypermesh中的边界条件即能施加到有限元模型上,也可以施加到几何模型上,两者产生的作用是一致的。
在有限元建模时,对行李架的结构进行了简化,只保留了纵梁、横梁和连接头三个主体部件。各个部件之间的连接,采用刚性接触来进行定义。如图8所示,为接头和纵梁的接触方式。分别在接头和纵梁上用于螺栓连接的部位创建Node集,并选择一个作为参考点,然后定义Node集中所有的节点的自由度关联到参考点。这样定义产生的结果就是接头和纵梁螺栓连接的地方具有相同的自由度,接头上的位移和载荷可有效地传递到纵梁上,即完成了接头和纵梁的连接的定义。其余各个部位的横梁和接头的连接也采用相同的方法进行刚性接触定义,如图9所示。
行李箱一般采用四角固定的方式安装在行李架横梁上。在有限元分析中,为了方便给行李架横梁施加重量载荷,采用自由度关联的方式,在两条行李架中心位置建立一个参考点,并将行李架横梁上用于安装固定行李箱的位置处的有限元网格的节点的自由度关联到参考点上,如图10所示。通过设置使它们具有相同的自由度,可有效地实现重量载荷平均的施加在行李架横梁上,而不需要在行李架横梁上的载重位置分别施加载荷。
2.5分析控制
在几何模型、材料属性、有限元网格、单元属性、边界条件等参数都建立完成之后,就完成了完整的有限元模型,可以递交Nastran进行运算分析了。根据企业子系统分析规范给行李架的有限元分析制定的11种具有代表性的受载形式,建立11个Subcases,1个Subcase中定义一个工况,分别施加不同的载荷形式,并设置相应的分析类型和参数设置,定义应力、应变和位移等输出,具体见下节论述。
3 行李架结构有限元分析
行李架结构在使用过程中可能出现的失效形式为行李架横梁的刚度失效和强度失效。刚度是指汽车车身结构的载荷与车身行驶时造成的变形之间的关系特性。作为承重部件,行李架的结构在设计时必须考虑具有足够的强度和刚度,从而应对其疲劳寿命、总成装配和客户使用的各种需求。汽车在不同工况下行驶过程中会遭受到各种各样的加载载荷,如各类不同的路况(山路,涉水,碎石,柏油等),且会遭遇各种操控如颠簸、急刹、拐弯等,如果刚度不足,会引起行李架结构的变形,无法满足企业标准要求。当产生一定程度的变形时会引起应力集中,导致行李架结构的失效。因此,研究和分析行李架结构的刚度和强度,有着十分重要的意义。

图7 某中型SUV行李架主体结构有限元网格图

图8 定义接头和纵梁的接触方式

图9 定义横梁和接头的接触方式
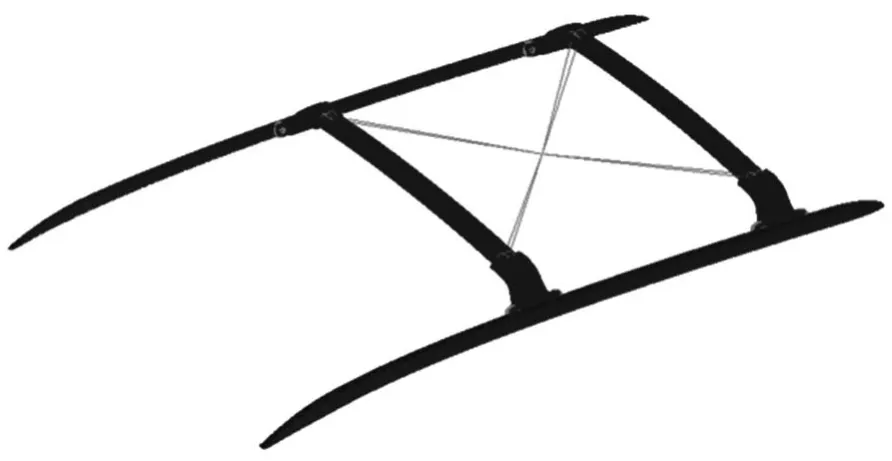
图10 用于施加载荷的参考点设置
11种不同的载荷形式如表1所示,载荷等级参照表1中的50 kg等级进行有限元分析。以下就工况1进行详细分析。
3.1 工况1:735 N垂直载荷(目标值:最大形变<10 mm)
该工况模拟正常装载货物情况,在车辆的中心线,并跨越前后部横梁分布的垂直载荷735 N,加载方式如图11所示。约束行李架纵轨上6个固定点的所有自由度。采用有限元分析垂直加载下行李架横梁的最大变形量和应力分布。
分析结果的位移分布和应力分布分别如图12和图13所示,可以看出位移和最大应力满足设计要求,没有损坏现象。其中位移变化最大位移为0.228 5 mm,满足要求值10 mm,主要集中在后梁,由于集中力方向竖直向下,主要原因在于前后梁的水平高度差,在实际安装过程中,尽量使前后梁的水平高度差降低。最大应力为21.4 MPa,没有出现损坏。
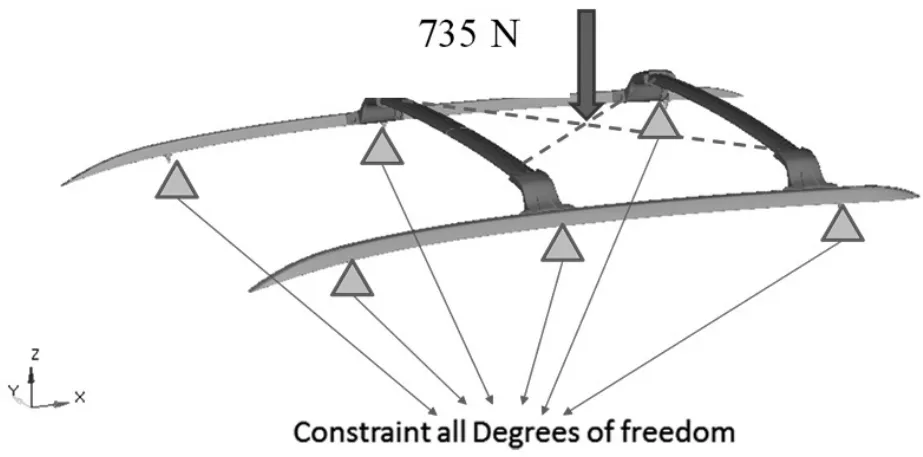
图11 工况1下的载荷方式示意图

图12 工况1下位移分布示意图
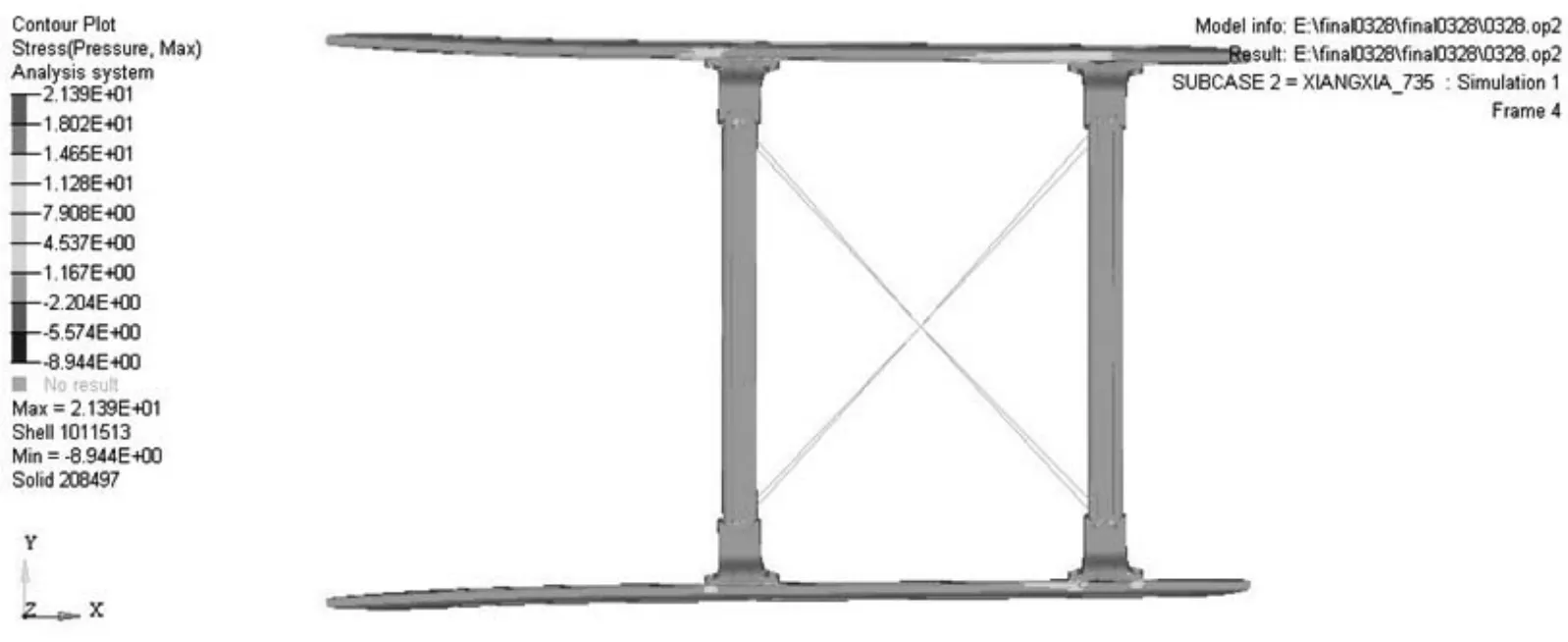
图13 工况1下应力分布示意图
其他10个工况依据此方法进行有限元分析,其结果都符合标准的要求,具体数值如表4所示,图14为数据对比图。
根据以上测试方法,收集11种不同工况下行李架横梁的位移值,都远小于标准的要求值,即该行李架结构设计满足要求,可以放心地进行下一步开模。
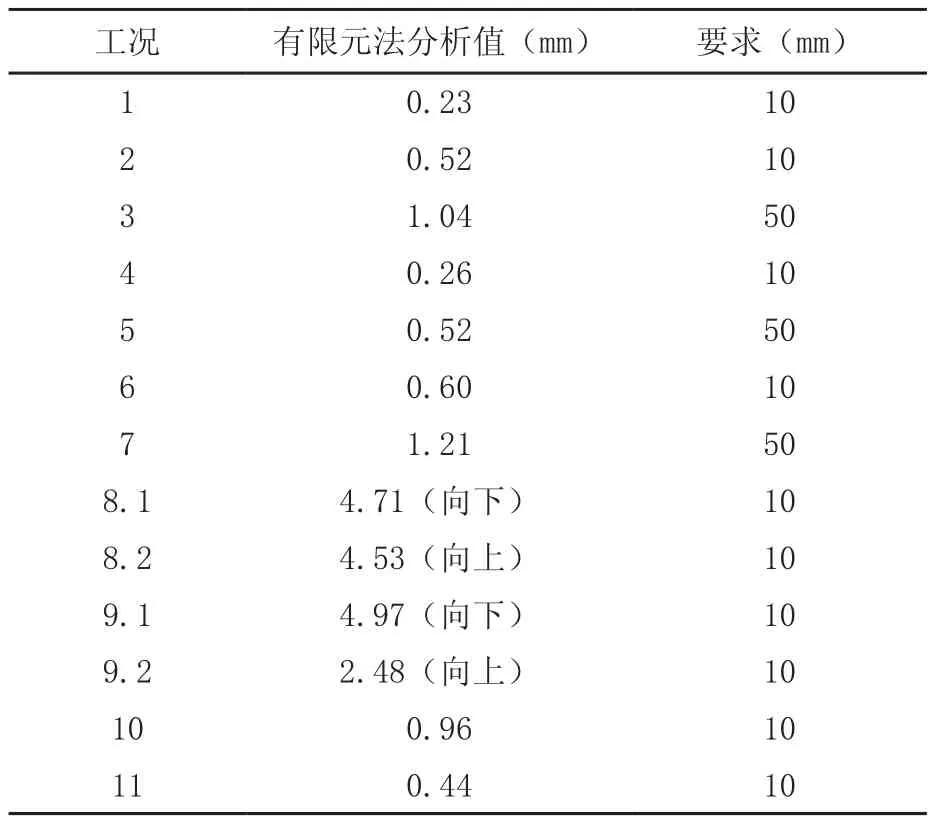
表4 有限元分析位移值
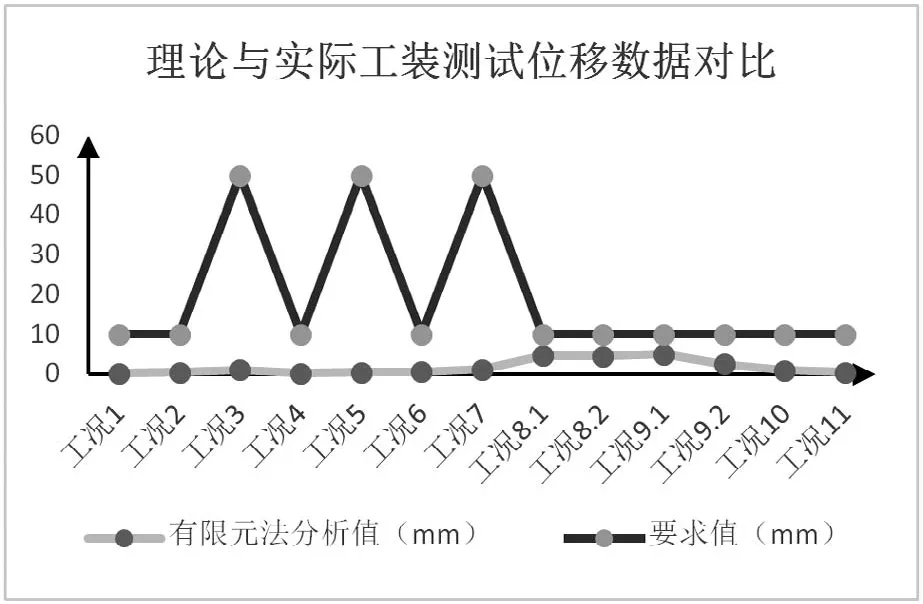
图14 有限元法分析值与要求值对比图
4 研究总结与展望
在现代车辆结构设计和分析方法中,有限元分析法在前期设计和性能测试方面有着非常重要的作用,是CAE虚拟设计和开发的重要环节。将有限元方法应用于汽车结构开发和测试已经成为各大主机厂的首选,也是缩短产品设计开发周期、降低研发成本、提高产品设计质量的必由之路。
有限元法在汽车结构设计和开发的应用中是一个范围很广泛的研究课题。本文对行李架的承载功能进行了有限元分析,只是涉及到了行李架结构设计和分析中一部分,在深度和广度上还有待于进一步研究。今后的研究目标主要有以下几个方面:
1)本文只是针对行李架结构的主体部件包括行李架横梁、纵轨和连接件进行了有限元建模,鉴于有限元分析成本,其余部件在有限元分析中都进行了简化,着重考察了行李架横梁的强度和刚度。根据实际工况的分析需求,以后还应该将车身考虑进来,同时结合材料的非线性特性进行分析,以进一步提高分析精度。
2)汽车的振动将带来噪声,影响汽车舒适度。更严重地振动工况会造成连接结构的共振和疲劳,当达到一定量级会产生不可逆的破坏,因此了解车身及产品本身的固有频率,将可以有效提高避免结构设计中由于振动造成的损失。因此对行李架结构模态分析也是很有必要的。
[1] 雅坤. 行李架知识[J]. 世界汽车, 2009 (3):128-131
[2] 林祥亮. 话说汽车行李架[J]. 家用汽车, 2006, (6):5-8
[3] 崔俊芝.计算机辅助工程(CAE)的现在与未来[J].计算机辅助设计与制造, 2000,(6):3-8.
[4] 张力.计算机辅助工程在产品发展中的综合应用与研究[D].重庆:重庆大学, 1996,(7).
[5] 谭继锦,张代胜. 汽车结构有限元分析[M]. 北京:清华大学出版社, 2009.
[6] Dereje Agonafer, J.Arnold Free. Numerical modeling of an entire thermal conduction module using a thermal coupling methodology[C]. ASME International Mechanical Engineering Congress.1995. Vol.236. No.9: 82-87 .
[7] Mori M. The finite element method and its applications[R].New York: Macmillan Pub Co, 1983.
[8] Noboru Hikosaka. A View of the Fracture of Automotive Diesel Engine[C]. SAE Transaction 972682. 1997: 2071-2081.
[9] 余俊.现代设计方法及应用[M].北京:中国标准出版社,2002.10.
[10] (美)艾金, J.E.有限元法的应用与实现[M].北京:科学出版社, 1992, 8.
