连线读点补矩法在施工期洪水中的应用

王晶晶

（辽宁省水利水电勘测设计研究院，辽宁沈阳 110006）

连线读点补矩法在施工期洪水中的应用

王晶晶

（辽宁省水利水电勘测设计研究院，辽宁沈阳 110006）

我国设计洪水频率分析的线型一般采用P-III分布，矩法初步估计参数，而矩法估计参数存在矩差。本文采用连线读点补矩法，进行矩差修正，提高了估计精度。通过在桓仁水库坝址的实例应用，表明绘线读点补矩法在施工期设计洪水中具有一定的适用性。

设计洪水；P-III分布；矩法；连线读点补矩法；施工期

我国设计洪水频率分析的线型一般采用PIII分布，对于参数估计方法，在国外最具代表性的是概率权重矩法（PWM）[1]和线性矩法（L-M）[2]；国内则是适线法[3]、概率单权函数法[4-5]和双权函数法[6]，实际应用中以矩法初步估计参数，经验适线法确定参数为主[7]。

1 连线读点补矩法

1.1 矩 法

参数估计是指采用经验频率公式在机率格纸上点连洪水系列后，选定频率曲线线型后，估计其中所含的统计参数。我国设计洪水频率分析的线型一般采用P-III分布，参数有均值x，变差系数Cv和偏态系数Cs。在实际工作中，除了n年连续观测资料外，通常还有若干次特大（历史）洪水。对于这种不连续系列，x和Cv两个参数的样本估计为：

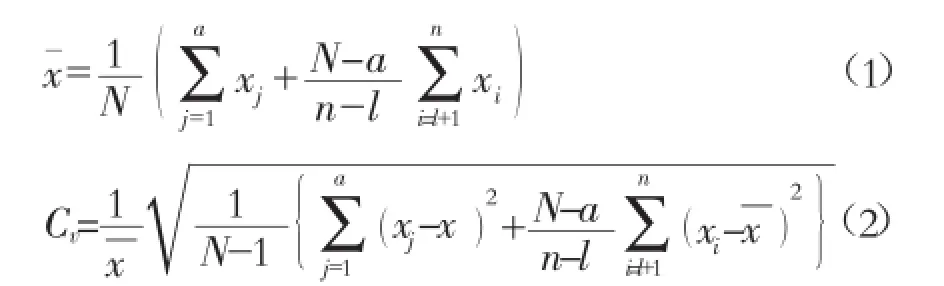
式中：N——历史洪水调查考证期长度，年；a——特大历史洪水个数；l——出现在n年连续观测期中，已作特大洪水处理的洪水个数；Cs——一般不用矩法估计，而是参考地区规律选定一个Cs/Cv的比值。1.2连线读点补矩法

由于矩法估计参数存在“求矩差”，由此所得的频率曲线总是系统偏小，其中尤以Cs偏小更为明显。“求矩差”是由于以有限和形式的样本矩代替连续频率曲线矩和使用的经验频率公式把（0，1）区间分成n+1等分而不是n等分的积分表达式而引起的。因而，“求矩差”不是随机误差，是一种系统的计算误差。只有当n→∞时才会消失[8]。

《水文频率计算常用图表》[9]给出了求矩差的表达式，用下列公式求得：

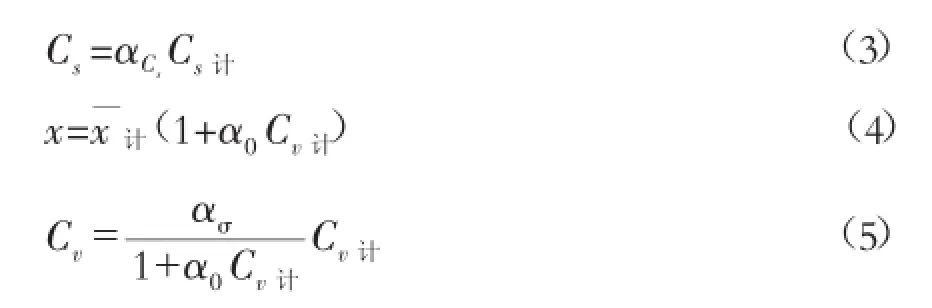
上述公式中，αCs，α0及ασ都与Cs和n有关，并已给出诺模图备查。

具体计算时，首先在目估和徒手绘得的频率曲线上，读出n个xm值（m=1，2，…，n），按此n个值用矩法计算3个参数x计，Cv计和Cs计，用上述公式求得加求矩差后的3个参数x、Cv和Cs。

2 实例研究

2.1 流域概况

浑江位于吉林省的南部和辽宁省的东部，是鸭绿江下游右侧的一条大支流。发源于长白山脉西南龙岗山的南麓，自东北流向西南，经白山、通化市于东村以下进入桓仁水库，桓仁水库以下为西江、凤鸣、东方红、回龙山、太平哨等梯级电站，然后转向东南，于桓仁县沙尖子下游50 km处注入鸭绿江。

桓仁水库位于浑江中游，控制流域面积1.04万km2，总库容34.6亿m3，为不完全调节水库。工程主要任务是发电，并兼顾防洪、灌溉、养殖等。

2.2 桓仁水库坝址施工期洪水

根据施工的要求及洪水特性，此次需要计算桓仁水库的施工期洪水。施工期洪水分为两期，即9月10日至12月和次年的1至6月，此次洪水选样选择相应期限内的年最大值。

桓仁水库上游有3个水文站，分别是八道江、通化和东村，均位于浑江干流上，其中八道江以上流域面积是1 306 km2，占桓仁水库面积的13%；通化以上流域面积4 722 km2，占桓仁水库面积的45%；东村以上流域面积是6 746 km2，占桓仁水库面积的65%。八道江以上流域面积较小，此次桓仁水库施工期洪峰分别采用通化和东村面积比的2/3次方进行计算，其中通化站资料系列为1957—1988年及2006—2013年，共计40年；东村站资料系列为1957—1966年及1969—1988年，共计30年。

通化站、东村站施工期洪水采用矩法和连续读点补矩法（简称补矩）的洪峰频率曲线图，见图1。

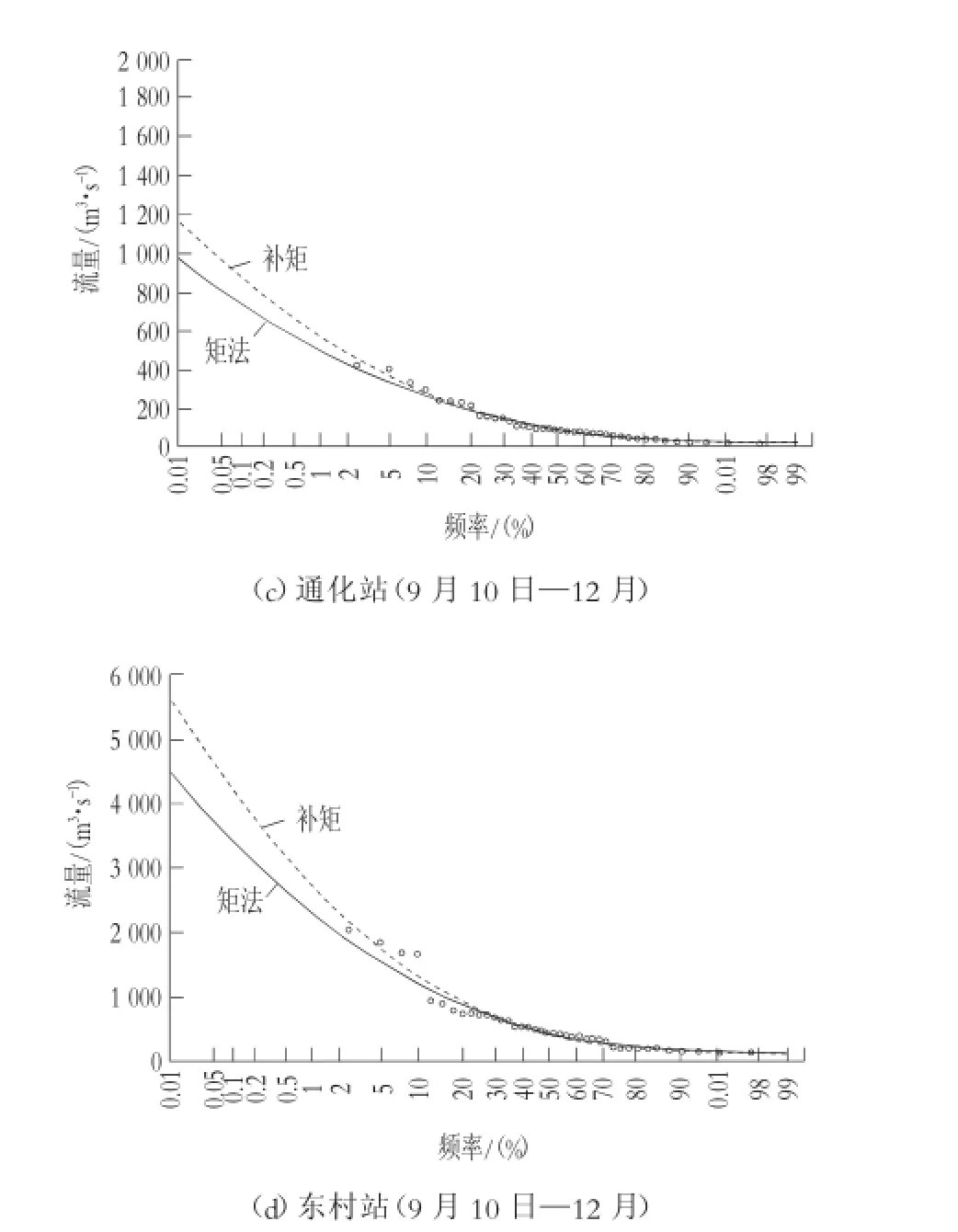
图1 通化站与东村站施工期洪峰流量频率曲线图

从图1可以看出，由矩法估计的参数及由此得出的频率曲线总是系统偏小，而连线读点补矩法可以修正这种矩差，计算结果更加合理，从而提高了频率分析效率和估计精度。

桓仁水库坝址施工期设计洪水成果见表1。

表1 桓仁水库坝址施工期设计洪水成果表

3 结论

由矩法估计的参数及由此得出的频率曲线系统偏小，连线读点补矩法可以修正这种矩差，提高了频率分析效率和估计精度。但任何一种估计方法都不可避免的包含有相当的误差（包括随机误差、计算误差或系统误差等），因此应尽量分析比较本站洪峰流量与各时段的洪量频率分析成果、上下游及临近流域频率分析成果和暴雨频率分析成果，经综合平衡后采用。

［1］GREENWOOD J A，LANDWEHR J M，MATALAS N C，WALLIS J R．Probability weighted moments:definition and relation to parameters of several distribution excressible in inverse form.Water Resource Research，1979，15（5）：1049—1054.

［2］Hosking J R M，Wallis J R.Regional frequency analysis．Cambridge University Press，1997：14—41

［3］黄振平．水文统计学［M］（1版）．南京：河海大学出版社，2003．

［4］马秀峰．计算水文频率参数的权函数法［J］．水文，1984，4（3）：1—11.

［5］宋德敦，丁晶．概率权重矩法及其在P－III分布中的应用［J］．水利学报，1988，19（3）：1—11.

［6］刘光文．P-Ⅲ型分布参数估计［J］．水文，1990，10（4）：1—10.

［7］王晶晶，梁忠民，等．基于熵法的入流预报误差规律研究［J］．水电能源科学，2010，28（7）：12—14.

［8］能源部水利部水利水电规划设计总院．水利水电工程设计洪水计算手册［M］（1版）．北京：水利电力出版社，1995．

［9］水利水电科学研究院．水文频率计算常用图表［M］（1版）．北京：中国工业出版社，1966．

TV122

A

2016-05-17