Bifurcation Analysis for a Free Boundary Problem Modeling Growth of Solid Tumor with Inhibitors

WANG ZE-JIA,XU JIAN-LEI AND LI JING-HUA

(College of Mathematics and Information Science,Jiangxi Normal University, Nanchang,330022)

Bifurcation Analysis for a Free Boundary Problem Modeling Growth of Solid Tumor with Inhibitors

WANG ZE-JIA,XU JIAN-LEI AND LI JING-HUA

(College of Mathematics and Information Science,Jiangxi Normal University, Nanchang,330022)

Communicated by Wang Chun-peng

This paper is concerned with the bifurcation analysis for a free boundary problem modeling the growth of solid tumor with inhibitors.In this problem,surface tension coefcient plays the role of bifurcation parameter,it is proved that there exists a sequence of the nonradially stationary solutions bifurcate from the radially symmetric stationary solutions.Our results indicate that the tumor grown in vivo may have various shapes.In particular,a tumor with an inhibitor is associated with the growth of protrusions.

free boundary problem,bifurcation analysis,solid tumor

1 Introduction

During the past forty years,a number of mathematical models have been studied and developed,see review papers[1]–[5]and the references therein.Among those,the growth of solid tumor models,described by partial diferential equations with a free boundary,have been given considerable attention,see[6]–[21].Solid tumor growth can be regarded as a result of various interactions within the micro environment,such as nutrient(e.g.oxygen,glucose), or inhibitors(e.g.inhibitory material developed from the immune system of healthy cells, anti-cancer drugs and radiation administered by medical treatment),etc.

In this paper,we consider a mathematical model describing the stationary state of anavascular solid tumor with inhibitor:

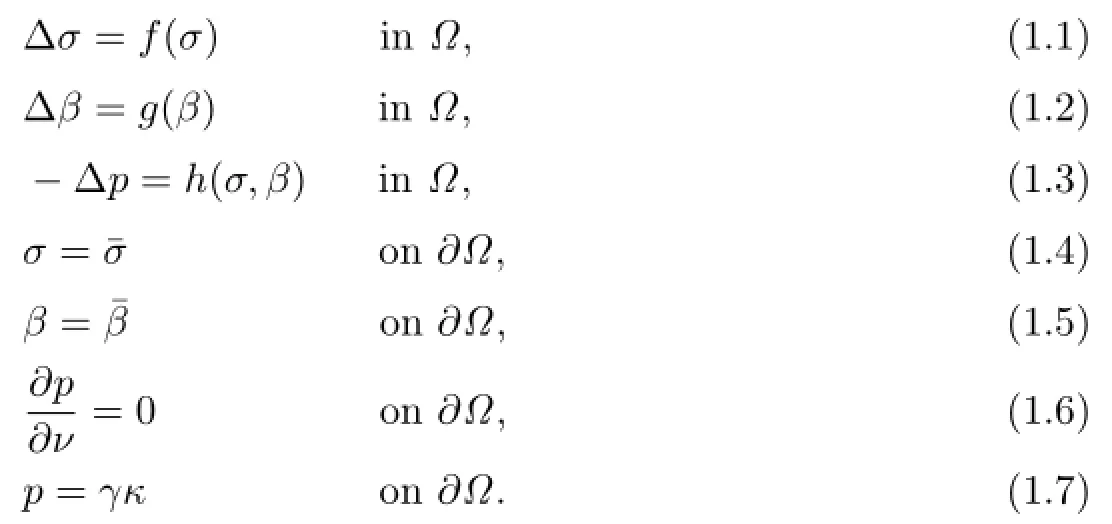
In this model,Ω⊆R3is the domain occupied by the tumor.σ,β denote the concentration of nutrient and inhibitor within the tumor,respectively.The pressure p within the tumor comes from the proliferation of the tumor cells.f(σ),g(σ),h(σ,β)are the nutrient consumption rate,inhibitor consumption rate and tumor-cell proliferation rate function,respectively. ¯σ and¯β are positive constants,σ=¯σ and β=¯β mean that the tumor receives constant nutrient and inhibitor supply from the exterior surface,respectively.ν is the outward normal of the free boundary∂Ω,γ is the surface tension coefcient,and κ is the mean curvature of the free boundary∂Ω.

According to the medicine and biology,as well as the need of the mathematics,we assume that f,g,h are functions satisfying the following conditions:

(A1)f∈C∞[0,∞),g∈C∞[0,∞),h∈C∞([0,∞)×[0,∞));

(A2)f′(σ)＞0 for σ≥0 and f(0)=0;

(A3)g′(β)＞0 for β≥0 and g(0)=0;

f(σ)is strictly monotone increasing about σ means the concentration of nutrient is much larger,the tumor cells consume more nutrient in the unit time.f(0)=0 means the nutrient consumption is zero when there is no nutrient,we can make similar explanation for g(β). h(σ,β)is strictly monotone increasing about σ and decreasing about β means increasing the concentration of the nutrient and inhibitor will enlarge and lower the proliferation rate of the tumor cells,respectively.h(0,0)＜0 means that the number of tumor cells decreases when the concentration of nutrient and inhibitor are all zero.Obviously,these assumptions satisfy the medicine and biology principle.

For the system(1.1)–(1.7)without inhibitors,i.e.,β=0,the authors of[13],[15]and [16]studied the linear case:f(σ)=σ,h(σ)=µ(σ−~σ),and proved the existence of a unique radially symmetric solution and a sequence of nonradially stationary solutions for this system in two-dimensional case and three-dimensional case respectively.In[11],the above results were extended to general case with f(σ),h(σ)are smooth functions.For the case β/=0, the existence of radially symmetric stationary solutions and nonradially stationary solutions were analysed for the linear case of(1.1)–(1.7)by Cui et al.in[10],[12],[20]and[21].For general case of(1.1)–(1.7),the existence of the radially symmetric solutions was studied byWei and Cui in[19].In this paper,we study the existence of nonradially solutions of the problem(1.1)–(1.7).We shall regard(1.1)–(1.7)as a bifurcation problem with γ being the bifurcation parameter,and reduce this problem into the following bifurcation equation with the form:

where F is nonlinear operator.By studying the linearized problem,we compute all eigenvalues of its Fr´echet derivative DρF(0,γ),then applying Crandall-Rabinowitz bifurcation theorem(cf.Theorem 1.7 in[14]),we obtain that there exists a null sequence of numbers {γk},and an integer k∗≥ 2 such that in a neighborhood of each γkwith k≥k∗,the problem(1.1)–(1.7)has a branch of nonradially symmetric solutions bifurcating from the radially symmetric solutions.

The rest of this paper is organized as follows.In Section 2,we study the linearization of (1.1)–(1.7)at radially symmetric solution.In Section 3,we reduce problem(1.1)–(1.7)into the abstract form(1.8)and study the properties of the operators F(·,γ).In Section 4,we study bifurcation solutions and prove our main result.Some conclusions are also given in the last section.

2 Linearization

It was shown in[19]that there exists a unique radially symmetric solution(σ0(r),β0(r), p0(r),Ω0)of the problem(1.1)–(1.7)with Ω0={x∈R3:|x|＜Rs}.In this section,we determine the linearization of the problem(1.1)–(1.7)at the radially symmetric solution. We also provide conditions which imply that the linearized problem has nontrivial solutions.

For S(ω)∈S2,denote Ωε={x∈R3:r＜Rs+εS(ω)},we consider the perturbations of the radially symmetric solution(σ0(r),β0(r),p0(r),Ω0)of the form

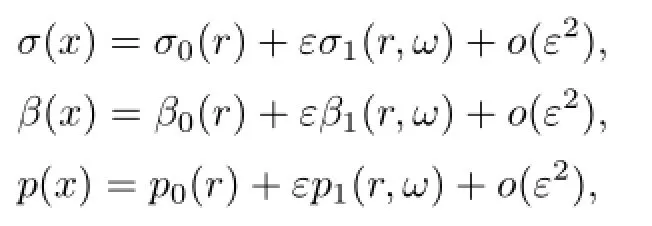
we can get that the linearizations of(1.1)–(1.7)satisfy the following:

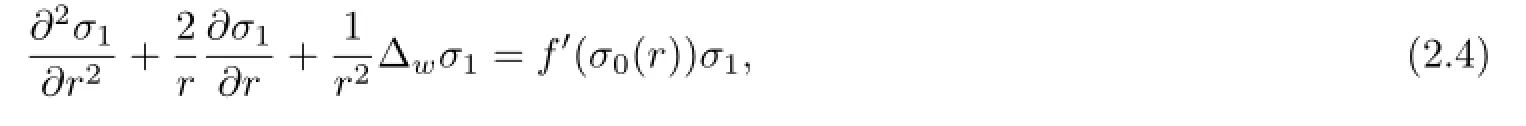
Thus we have the following result.

Lemma 2.1The linearization of the problem(1.1)–(1.7)at the radially symmetric solutions(σ0(r),β0(r),p0(r),Ω0)is given by the problem(2.4)–(2.10).

We now investigate the question of whether there exists γ such that the problem(2.4)–(2.10)has nontrivial solutions.For this purpose we frst note that standard results for second order elliptic partial diferential equations imply that all solutions σ1,β1,p1are smooth,namely,σ1,β1,p1∈C∞(¯BRs)⊆C∞([0,Rs],C∞(S2)),and S∈C∞(S2).Thus these functions can be expanded in the following way:

where Ykl(ω)(k≥0,−k≤l≤k)denotes the spherical harmonics of the order(k,l). Substituting(2.11)–(2.14)into(2.4)–(2.10),using the relation

we get

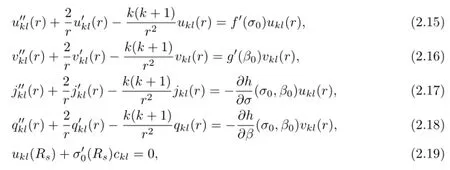
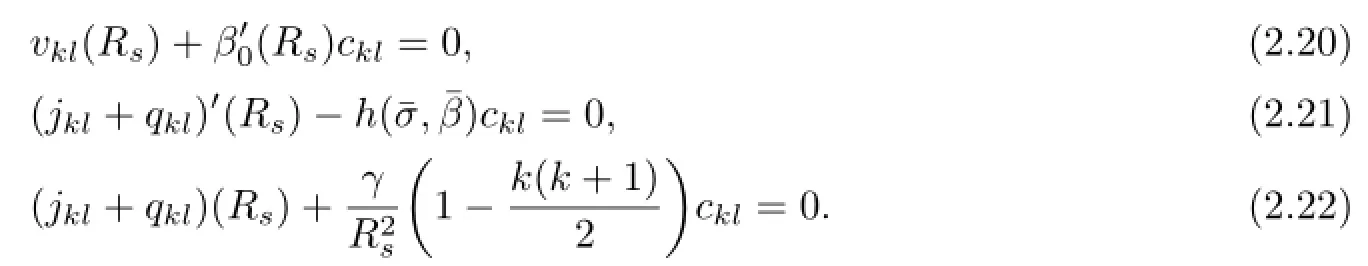
and

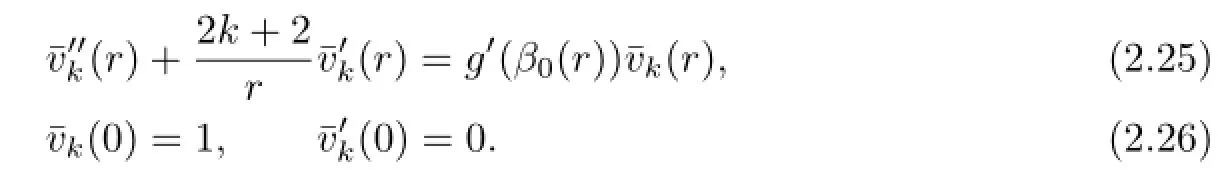
Denote

then ukl(r),vkl(r)satisfy the equations(2.15)and(2.16),where akl,bklare arbitrary constants.

Similarly,the solutions of(2.17)-(2.18)are given by:

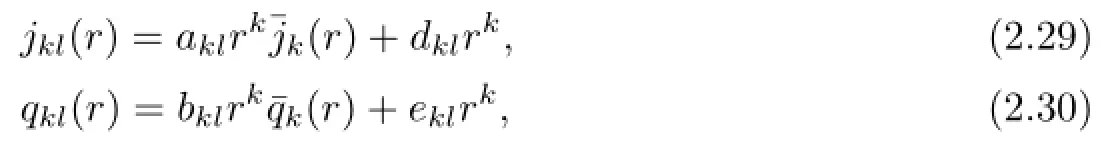
where aklis as before,dkl,eklare arbitrary constants proportional to akland bklfor an arbitrary constant c,respectively,and jkl(r)is the following boundary value problem

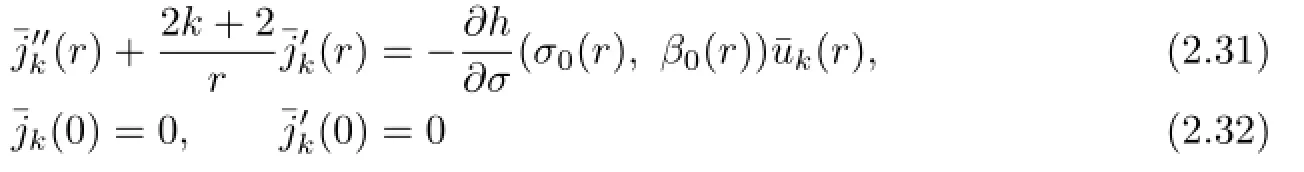
and qkl(r)is the solution of the following problem

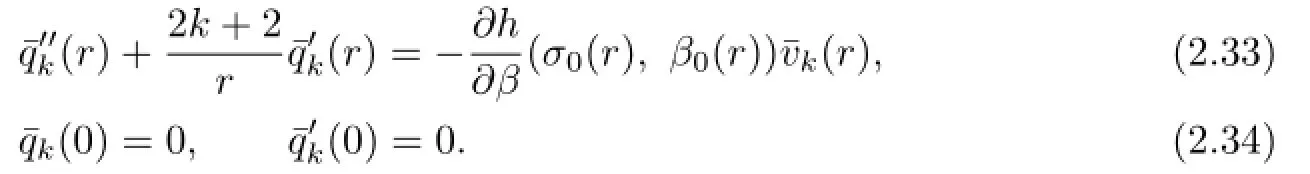
Substituting(2.27)-(2.28),(2.29)-(2.30)into(2.19)–(2.22),after simplifcation,we get the following equation for akl,bkl,ckl,dkl+eklsatisfying:

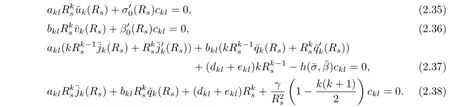
Hence,(2.4)–(2.10)has a nontrivial solution if and only if there exists k≥2 such that (2.35)–(2.38)has a nontrivial solution.In the following,we provide conditions on γ which guarantee that(2.35)–(2.38)has a nontrivial solution.

Lemma 2.2The system(2.35)–(2.38)has a nontrivial solution if and only if γ=γk, where

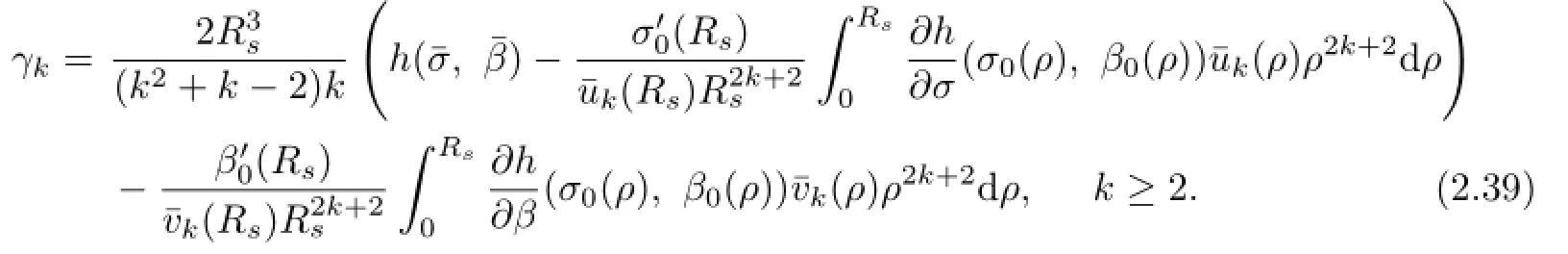
In this case,the nontrivial solutions of(2.35)–(2.38)are unique up to a constant factor. Moreover,there exists a positive integer k∗such that

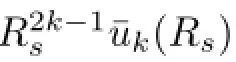
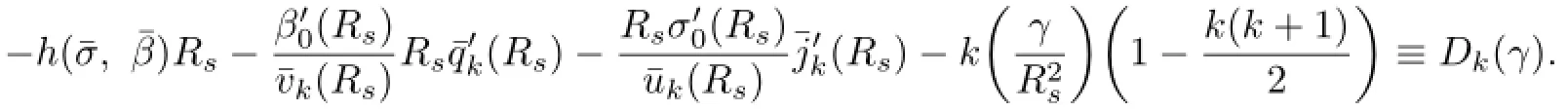
Hence,(2.35)–(2.38)has a nontrivial solution if and only if Dk(γ)=0,namely,

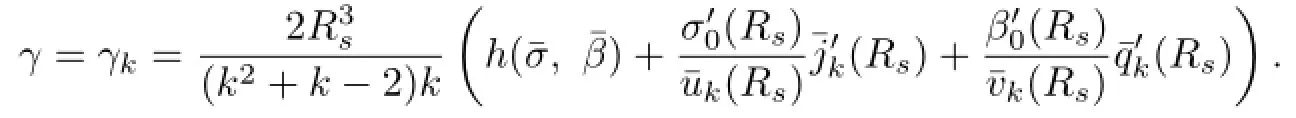
From(2.31)and(2.33)we further infer that

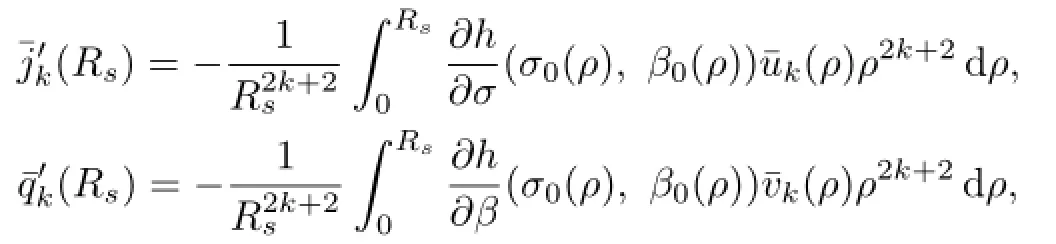
which implies that γkis given by(2.39).If γ=γk,then clearly the solutions of(2.35)–(2.38) are unique up to a constant factor.

To verify(2.40),we frst observe(2.23)and(2.25),which imply that

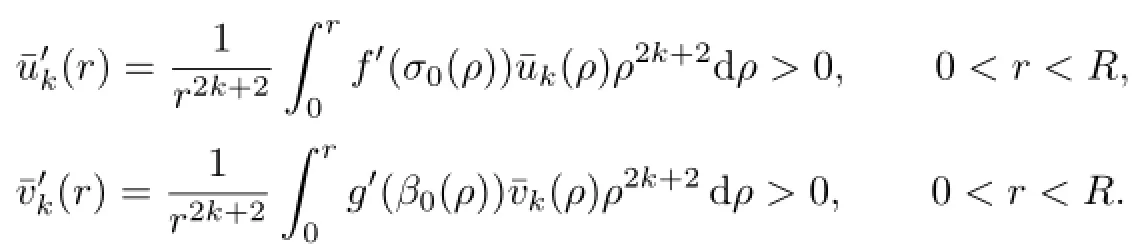
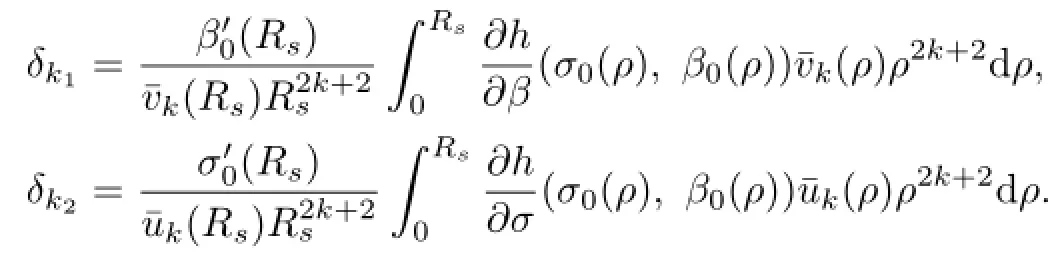
Integration by parts shows that

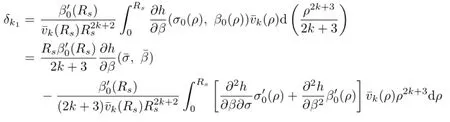
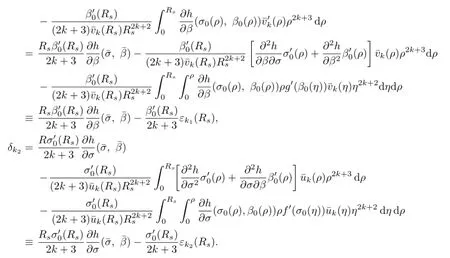
Since¯uk(r),¯vk(r)are increasing,we have

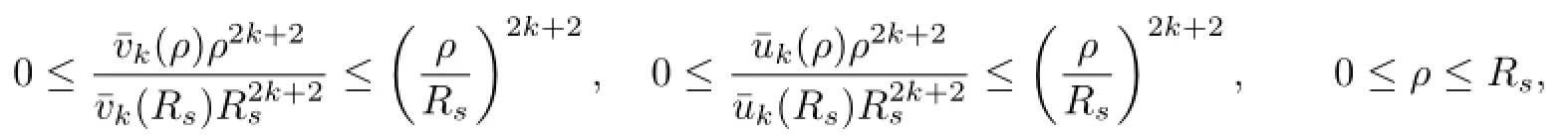
which implies that

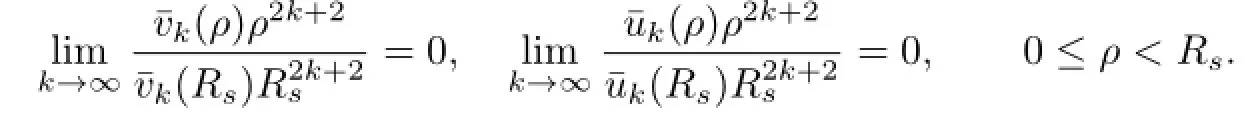
Hence,by dominated convergence,we see that

or

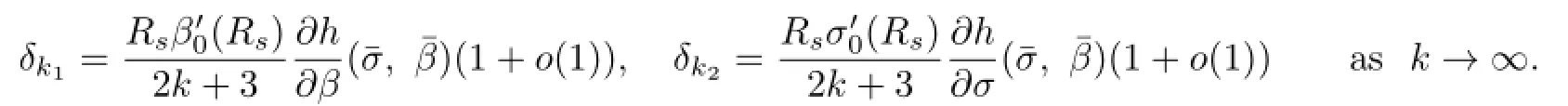
Substituting the above expressions into(2.39),we have

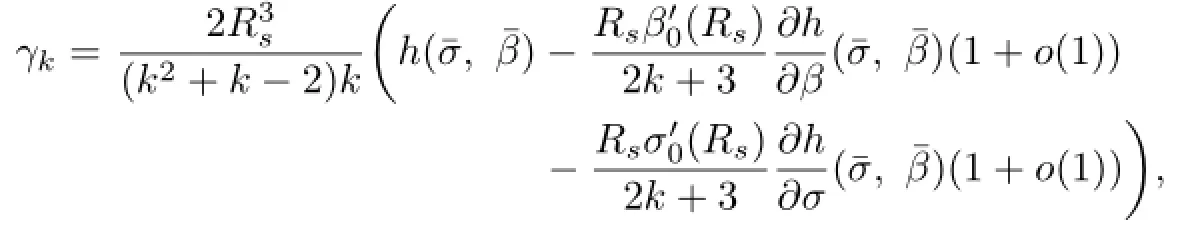
we deduce that

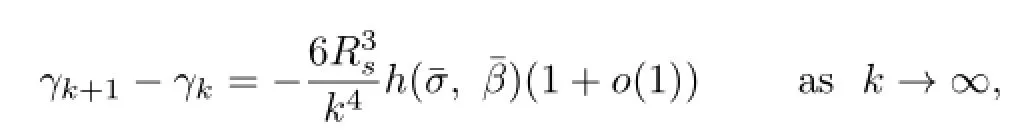
so that γkis strictly decreasing for k sufciently large.This is to say that there exists a positive integer k∗such that for k≥k∗,γk+1＜γk.This completes the proof of(2.40).

We now summarize the main result of this section.

Theorem 2.1The system of(2.4)–(2.10)has a nontrivial solution if and only if γ=γkfor some k≥2.

3 Reduction of the Problem

In this section,we perform the deduction of reducing problem(1.1)–(1.7)into an abstract equation of the form(1.8),and study properties of the operators F(·,γ).

Recall Ω0={x∈R3:|x|＜Rs}and∂Ω0={x∈R3:|x|=Rs}.We frst introduce the so-called Hanzawa transformation to convert the free boundary problem(1.1)–(1.7) into a nonlinear problem on the fxed domain Ω0.For this purpose,we take a function χ∈C∞[0,∞)such that

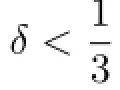
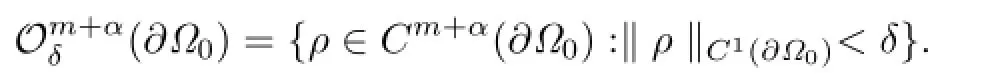
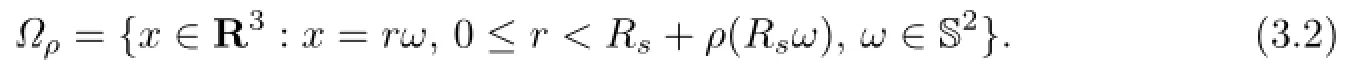
Now,the Hanzawa transformation Ψρ:R3→R3can be defned by Ψρ(0)=0 and

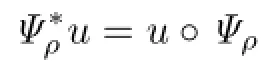
Clearly,if ρ∈Cm+α(∂Ω0),then

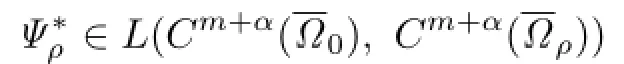
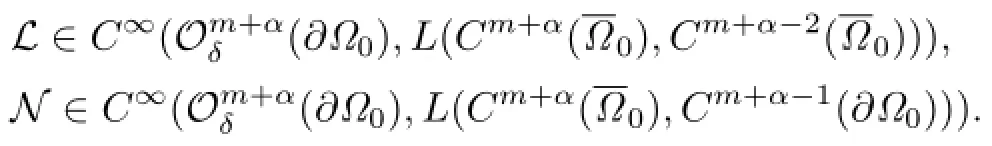
Finally,for ρ as mentioned earlier,we defne κ:Cm+α(∂Ω0)→Cm+α−2(∂Ω0)by κ(ρ)(Rsω)

={the mean curvature of the hypersurface r=Rs+ρ(Rsω)at the point(Rsω)}. Note that for any ω∈S2,we have

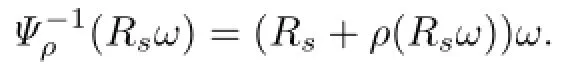
Using these notation,it is not difcult to verify that the Hanzawa transformation(3.2) converts problem(1.1)–(1.7)into the following equivalent system:

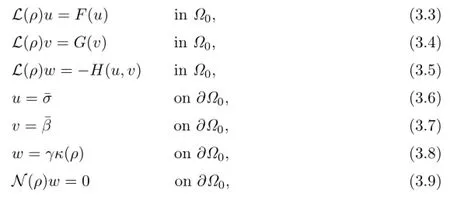
More precisely,we have

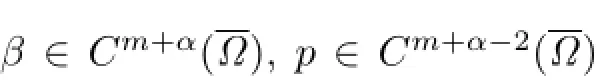
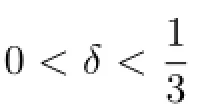
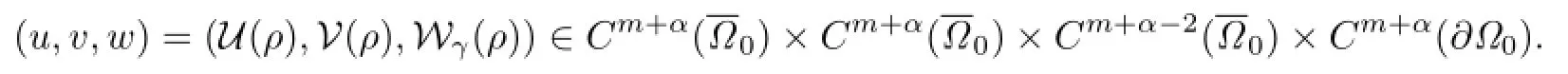
Substituting w=Wγ(ρ)into(3.9)and denoting F(ρ,γ)=N(ρ)Wγ(ρ),we obtain the following equation:

By the reduction and standard theory of elliptic equations,we can verify that

The following result will play an important role in later discussion:

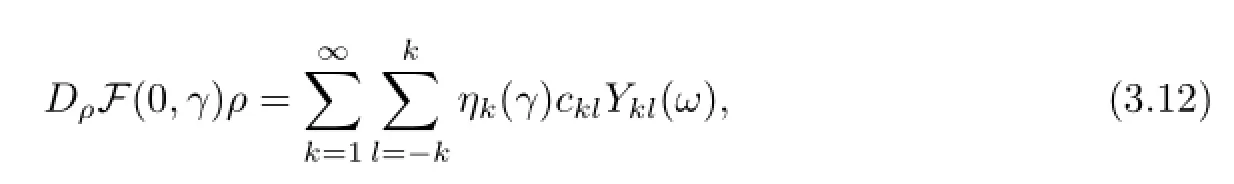
where

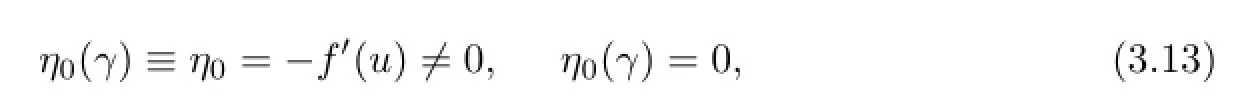
and

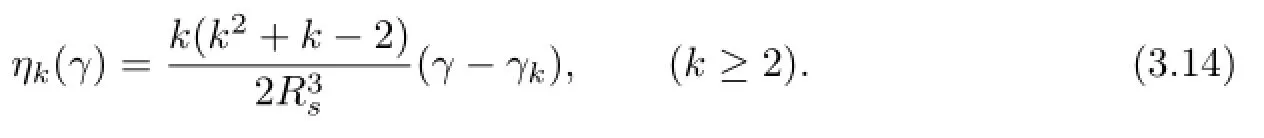
Proof. Because the equation(3.10)is equivalent to the problem(1.1)–(1.7),the linearization of(3.10)at ρ=0,that is,the equation DρF(0,γ)ρ=0,is correspondingly equivalent to the system of equations(2.15)–(2.22).Hence,from the deduction in Section 2,we see that DρF(0,γ)ρ has an expression of the form(3.12).Furthermore,this argument also shows that the coefcient of Ykl(ω)in the expression of DρF(0,γ)ρ,that is,ηk(γ)cklequals the left-hand side of(2.21),by a direct calculation,we obtain(3.13)and(3.14).

4 Bifurcation

In this section,we study bifurcation solutions for the problem(1.1)–(1.7).The main result of this paper is as follows:

Theorem 4.1Let(σ0,β0,p0,Ω0)be a radial solution of problem(1.1)–(1.7)satisfying(Rs)/=0.If h(σ,β)＞0,then there exists a null sequence of positive numbers γk{k≥k∗}, where k∗is an integer,k∗≥2,such that for each k≥k∗even,in an neighborhood of (σ0,β0,p0,Ω0,γk),there exists a bifurcation branch of solutions(σε,βε,pε,Ωε,γε)of problem (1.1)–(1.7)with the following form:

It should be pointed out that the bifurcation equation(3.10)is not of the classical type.By Lemma 3.2,we see that Fr´echet derivative DρF(0,γ)has a kernel of dimension 3, implying that DρF(0,γ)is always degenerate.Indeed,because any translation of a solution of(1.1)–(1.7)is still a solution,thus all solutions of(3.10)obtained from translating radial solutions make up a 3-dimension manifold,so it is natural.

For any m≥3 and 0＜α＜1,we introduce

X=the closure of the span{Yk0(ω),k=0,2,4,···}in Cm+α(∂Ω0),

Y=the closure of the span{Yk0(ω),k=0,2,4,···}in Cm−3+α(∂Ω0).

Note that in the spherical coordinates(θ,ϕ),0≤θ≤π,0≤ϕ≤2π,the spherical harmonics

where

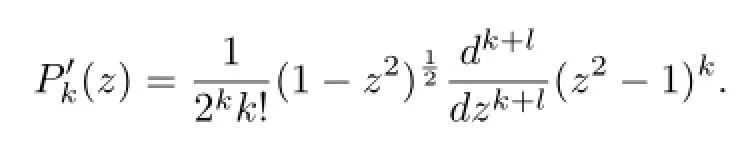
It is easy to verify that for k≥0 even,Yk0(θ,ϕ)is independent of ϕ and satisfes Yk0(θ)= Yk0(π−θ).Hence,for any function ρ∈X,ρ is independent of ϕ and ρ(θ)=ρ(π−θ).Using this fact and(3.11),we can verify that

Later we say γkis distinct if j/=k then γj/=γk.The following result holds:

Theorem 4.2For distinct γk(k≥k∗even),(0,γk)is a bifurcation point of the equation F(ρ,γ)=0.More precisely,there exists a constant ξk＞ 0 and a smooth mapping ε→(ρε,γε)from(−ξk,ξk)to X×R+of the form:

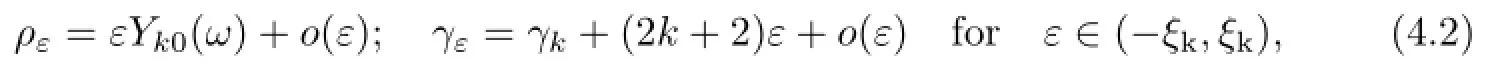
such that F(ρε,γε)=0.

Proof. By the reduction in Section 3 and the defnition of operator F(·,γ),it is clear that

From Lemma 3.2,we see that

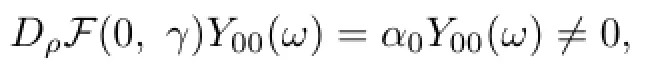
and

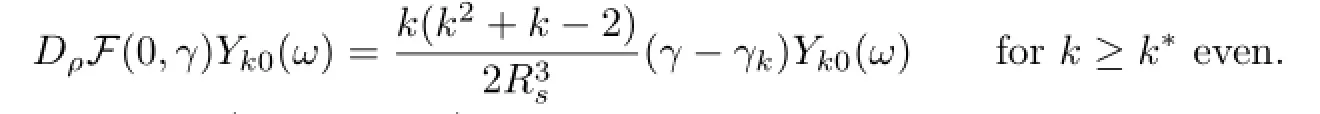
Hence,for distinct γk(k≥k∗even),we have

and

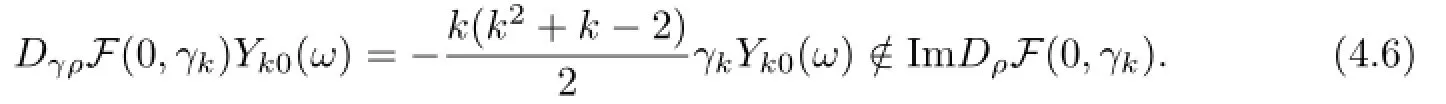
By(4.3)–(4.6),we see all suppositions of the well-known Crandall-Rabinowitz bifurcation theorem(Theorem 1.7 in[22])are satisfed,thus(0,γk)is a bifurcation point of the equation F(ρ,γ)=0,and the proof is completed.

Proof of Theorem 4.1Assume h(σ,β)＞0 and let k≥k∗even.By Lemma 2.2,we see that γkis distinct,so that(0,γk)is a bifurcation point of the equation F(ρ,γ)=0.Then by the reductions in Sections 2 and 3,the assertion of Theorem 4.1 follows.

5 Conclusion

Although the tumor model with inhibitor we studied is quite simple,we may nevertheless draw some interesting biological conclusions from the mathematical result.Tumors grown in culture are typically sphere.However,tumor grown in vivo may have various shapes.In particular,a tumor with an inhibitor is associated with the growth of protrusions.In our model,these protrusions are expressed by the shape r=Rs+εYm,0(θ,φ)+o(ε2)of the free boundary.We show that in case h(σ,β)＞0,there exist infnite many nonradial branches of solutions bifurcating at each γk(k≥k∗even).

[1]Araujo R P,McElwain D L S.A history of the study of solid tumour growth:The contribution of mathematical modelling.Bull.Math.Biol.,2004,66(5):1039–1091.

[2]Friedman A.A hierarchy of cancer models and their mathematical challenges.Discrete Contin. Dyn.Syst.Ser.B.,2004,4(1):147–159.

[3]Friedman A.Cancer models and their mathematical analysis.Tutorials in mathematical biosciences.III,223–246,Lecture Notes in Math.1872,Berlin:Springer,2006.

[4]Friedman A.Mathematical analysis and challenges arising from models of tumor growth.Math. Models Methods Appl.Sci.,2007,17:1751–1772.

[5]Lowengrub J S,Frieboes H B,Jin F,Chuang Y L,Li X,Macklin P,Wise S M,Cristini V. Nonlinear modelling of cancer:Bridging the gap between cells and tumours.Nonlinearity, 2010,23:1–91.

[6]Bazaliy B V,Friedman A.A free boundary problem for an elliptic-parabolic system:Application to a model of tumor growth.Comm.Partial Diferential Equations,2003,28(3-4): 517–560.

[7]Bueno H,Ercole G,Zumpano A.Asymptotic behaviour of quasi-stationary solutions of a nonlinear problem modelling the growth of tumours.Nonlinearity,2005,18:1629–1642.

[8]Byrne H M,Chaplain M A J.Free boundary value problems associated with the growth and development of multicellular spheroids.European J.Appl.Math.,1997,8(6):639–658.

[9]Cristini V,Lowengrub J,Nie Q.Nonlinear simulation of tumor growth.J.Math.Biol.,2003,46(3):191–224.

[10]Cui S.Analysis of a mathematical model for the growth of tumors under the action of external inhibitors.J.Math.Biol.,2002,44(5):395–426.

[11]Cui S,Escher J.Bifurcation analysis of an elliptic free boundary problem modelling the growth of avascular tumors.SIAM J.Math.Anal.,2007,39(1):210–235.

[12]Cui S,Friedman A.Analysis of a mathematical model of the efect of inhibitors on the growth of tumors.Math.Biosci.,2000,164(2):103–137.

[13]Fontelos M A,Friedman A.Symmetry-breaking bifurcations of free boundary problems in three dimensions.Asymptot.Anal.,2003,35(3-4):187–206.

[14]Friedman A,Bazaliy B.Global existence and asymptotic stability for an elliptic-parabolic free boundary problem:An application to a model of tumor growth.Indiana Univ.Math.J.,2003,52(5):1265–1304.

[15]Friedman A,Reitich F.Analysis of a mathematical model for the growth of tumors.J.Math. Biol.,1999,38(3):262–284.

[16]Friedman A,Reitich F.Symmetry-breaking bifurcation of analytic solutions to free boundary problems:An application to a model of tumor growth.Trans.Amer.Math.Soc.,2001,353(4): 1587–1634.

[17]Friedman A,Hu B.Bifurcation from stability to instability for a free boundary problem arising in a tumor model.Arch.Ration.Mech.Anal.,2006,180(2):293–330.

[18]Greenspan H P.On the growth and stability of cell cultures and solid tumors.J.Theoret. Biol.,1976,56(1):229–242.

[19]Wei X,Cui S.Asymptotic behavior of solutions for a free boundary problem modelling tumor growth.Acta.Math.Sci.,2007,27(4):648–659.

[20]Wang Z.Bifurcation for a free boundary problem modeling tumor growth with inhibitors. Nonlinear Anal.Real World Appl.,2014,19:45–53.

[21]Wu J,Cui S.Bifurcation analysis of a mathematical model for the growth of solid tumors in the presence of external inhibitors.Math.Models Methods Appl.Sci.,2015,38:1813–1823.

[22]Crandall M G,Rabinowitz P H.Bifurcation from simple eigenvalues.J.Funct.Anal.,1971,8: 321–340.

A

1674-5647(2017)01-0085-12

10.13447/j.1674-5647.2017.01.09

Received date:Feb.6,2016.

Foundation item:The NSF(11361029)of China and the NSF(20142BAB211001)of Jiangxi Province.

E-mail address:zejiawang@jxnu.edu.cn(Wang Z J).

2010 MR subject classifcation:35B35,35K35,35Q80