Bonnesen-style Isoperimetric Inequalities of an n-simplex

WANG WEN,CHEN YA-PINGAND YANG SHI-GUO

(1.School of Mathematics and Statistics,Hefei Normal University,Hefei,230601)

(2.School of Mathematical Science,University of Science and Technology of China, Hefei,230026)

(3.International Branch of Nan Men Primary School at Shangcheng,Hefei,231600)

Bonnesen-style Isoperimetric Inequalities of an n-simplex

WANG WEN1,2,CHEN YA-PING3AND YANG SHI-GUO1

(1.School of Mathematics and Statistics,Hefei Normal University,Hefei,230601)

(2.School of Mathematical Science,University of Science and Technology of China, Hefei,230026)

(3.International Branch of Nan Men Primary School at Shangcheng,Hefei,231600)

Communicated by Lei Feng-chun

In this paper,by the theory of geometric inequalities,some new Bonnesenstyle isoperimetric inequalities of n-dimensional simplex are proved.In several cases, these inequalities imply characterizations of regular simplex.

simplex,isopermetric defcit,Bonnesen-style isoperimetric inequality

1 Introduction

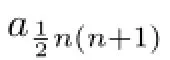
As a well known result,for a simple closed curve C(in the Euclidian plane)of length L enclosing a domain of area A,then

with equality holds if and only if the curve is a Euclidean circle.The quantity L2−4πA is said to be the isoperimetric defcit of C(see[1]–[3]).

As an extension,Bonnesen proved the following inequality(see[1]):

where R is the circumradius and r is the inradius of the curve C.Note that if the right hand side of(1.2)equals zero,then R=r.This means that C is a circle and L2−4πA=0.

More generally,inequalities of the form

are called Bonnesen-style isoperimetric inequalities if equality is only attained for the Euclidean circle(see[1]).See references[4]–[9]for more details.

When the simple closed curve C is a triangle(in the Euclidean plane)of area S and with side lengths a1,a2,a3,the following inequality is known:

Inequality(1.4)may be deemed isoperimetric inequality for triangles.

Veljan-Korchmaros inequality(see[10])concerning the volume and the edge lengths ofΩnstates as follows:

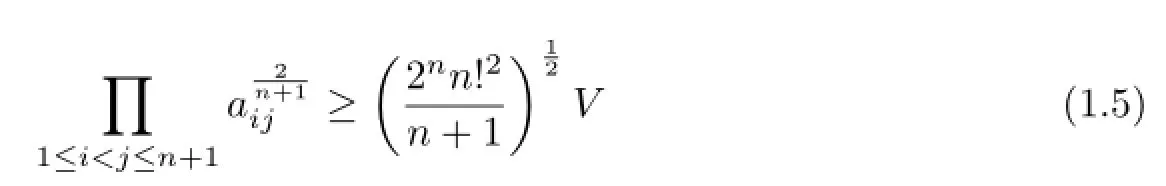
with equality holds if and only if Ωnis regular.

By utilize the arithmetic-geometric mean inequality to(1.5),we have

with equality holds if and only if Ωnis regular.

The inequality(1.6)may be deemed isoperimetric inequality of an n-simplex.The defcit value between the right-hand side and left-hand side of inequality(1.6)can be considered to be the isopermetric defcit for Ωn:

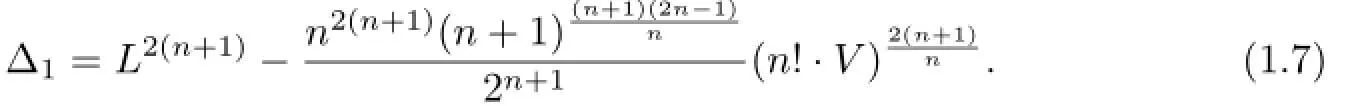
In addition,the volume V and the facet areas of the simplex Ωnsatisfy the following inequality:

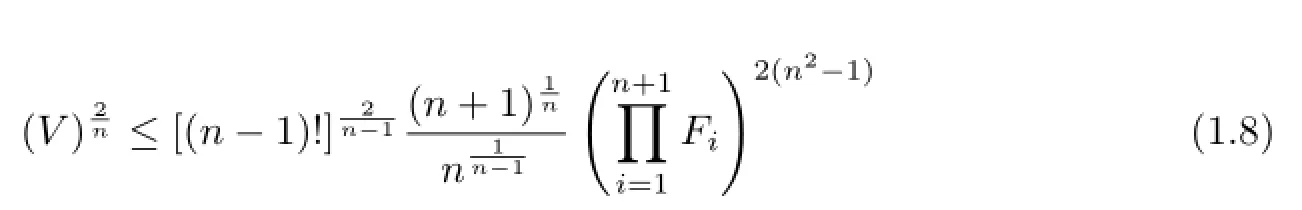
with equality holds if and only if Ωnis regular(see[11]).

By applying the arithmetic-geometric mean inequality to(1.8),we have

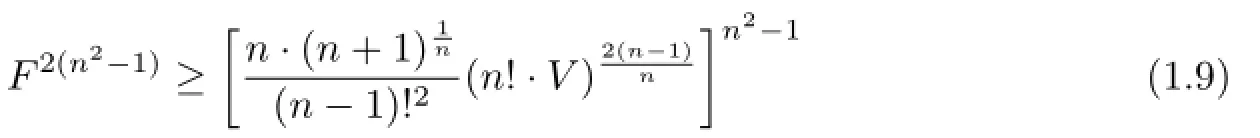
with equality holds if and only if Ωnis regular.

The inequality(1.9)may be also called isoperimetric inequality for an n-simplex.The defcit value between the right-hand side and left-hand side of inequality(1.9)can be regarded as the other isopermetric defcit for the n-simplex Ωn:

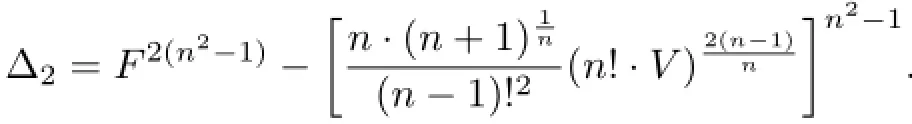
2 Main Results

Our main results are stated as follows.

Theorem 2.1Let Ωnbe an n-simplex.Then

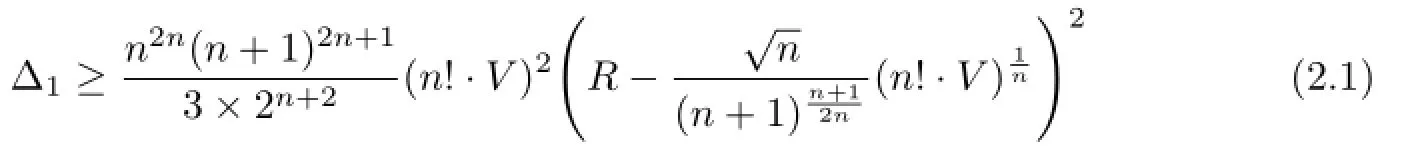
with equality holds if and only if Ωnis regular.

Theorem 2.2Let Ωnbe an n-simplex.Then

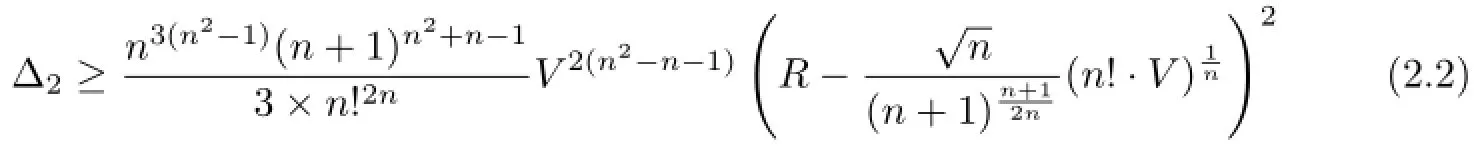
with equality holds if and only if Ωnis regular.

Corollary 2.1Suppose that ABC is a triangle of area S with the side lengths a1,a2,a3. Then

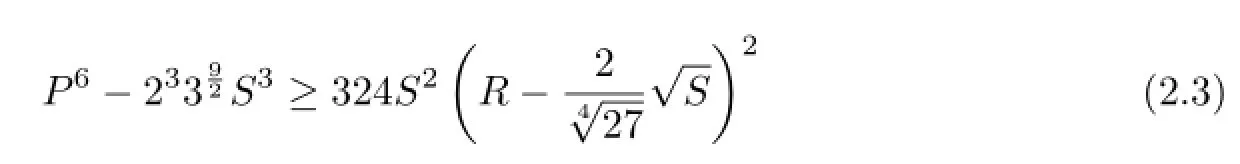
Corollary 2.2For a tetrahedron ABCD,we have

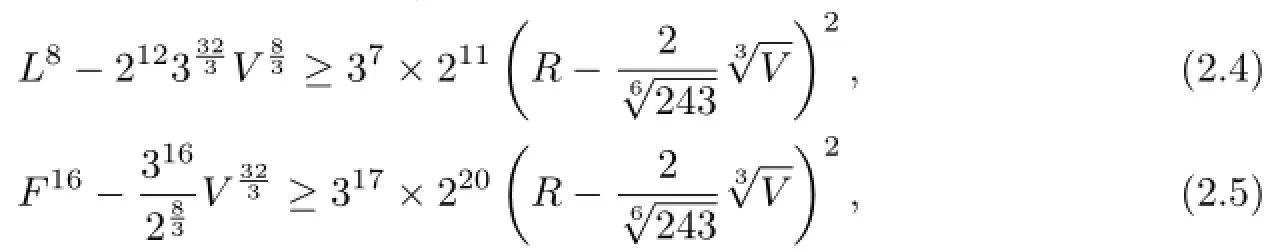
and the equalities are attained if and only if the tetrahedron is regular,where F is the surface area of ABCD.

3 The Proofs of Theorems

To prove the above theorems,we need some lemmas.

Lemma 3.1[11]For an n-simplex Ωn,we have

and the equalities are attained if and only if Ωnis regular.

Lemma 3.2[12]Let Ωnbe an n-simplex.Then

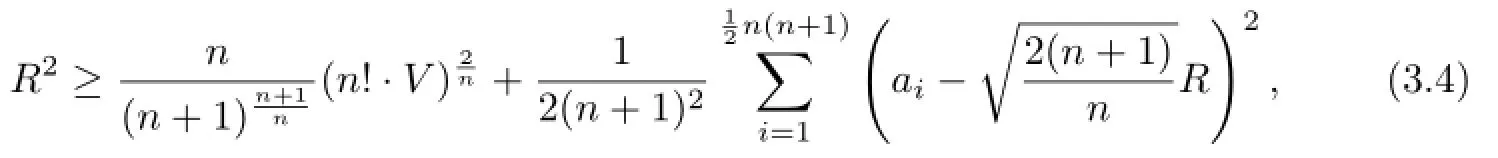
and the equality is attained if and only if Ωnis regular.

Lemma 3.3Let Ωnbe an n-simplex.Then

and the equality is attained if and only if Ωnis regular.

Proof. By suitable calculation,we get

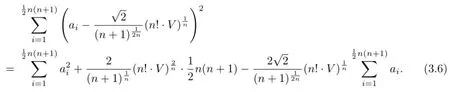
By(3.6),we have

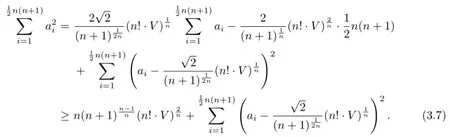
From(3.1)and(3.7),we get(3.5).

Lemma 3.4Let X,Y,Z be any real numbers.Then

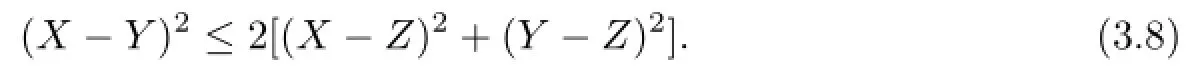
Proof. By using the absolute value inequality and the arithmetic-geometric means inequality,we get

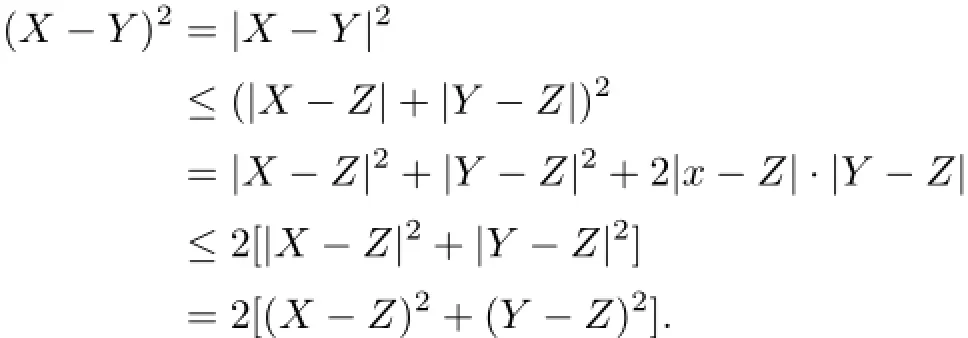
The Proof of Theorem 2.1By using the arithmetic-geometric means inequality,(3.2) and(3.4),we fnd that

On the other hand,we have

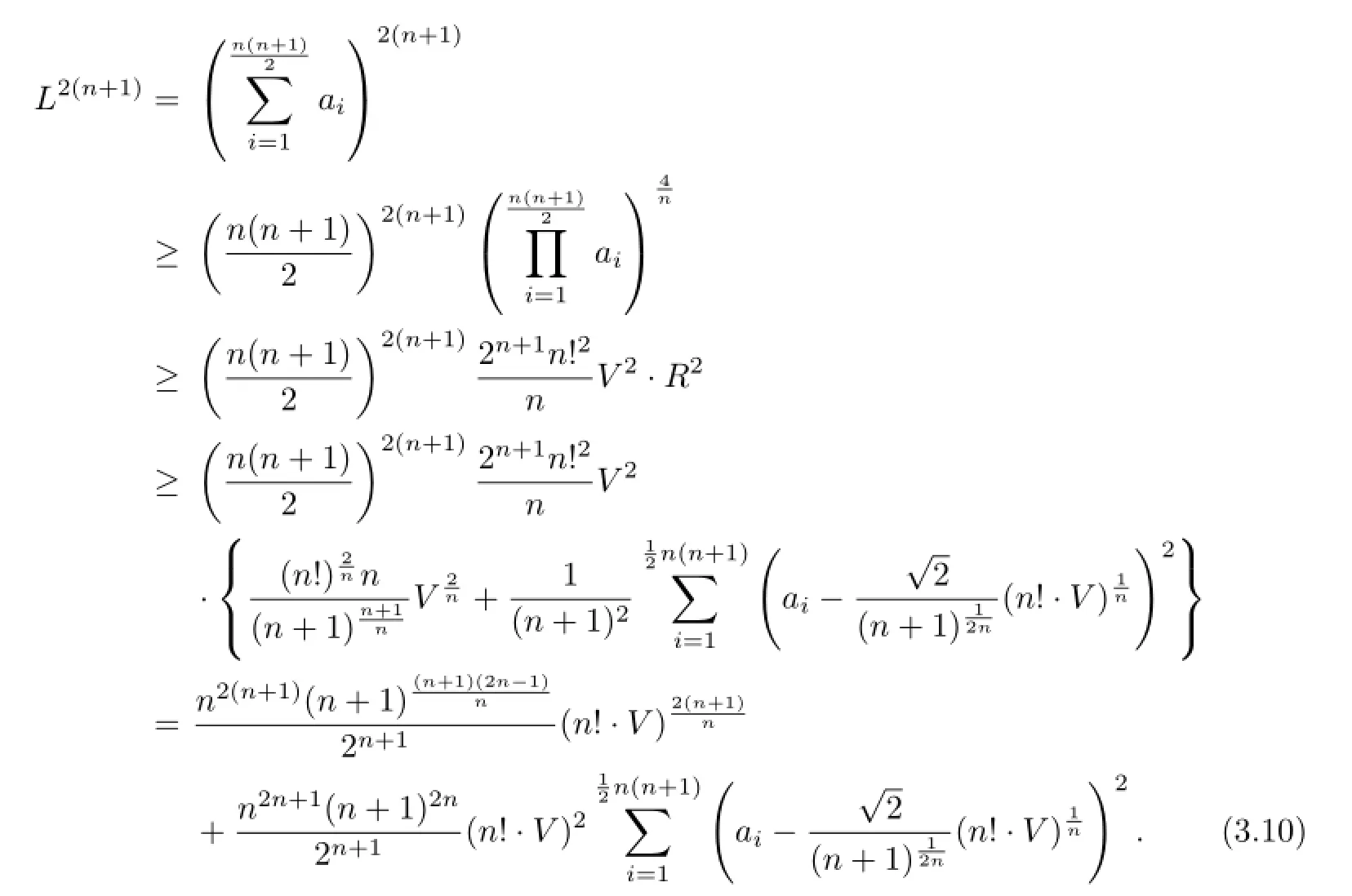
From(3.9)and(3.10),furthermore,applying(3.8),we obtain

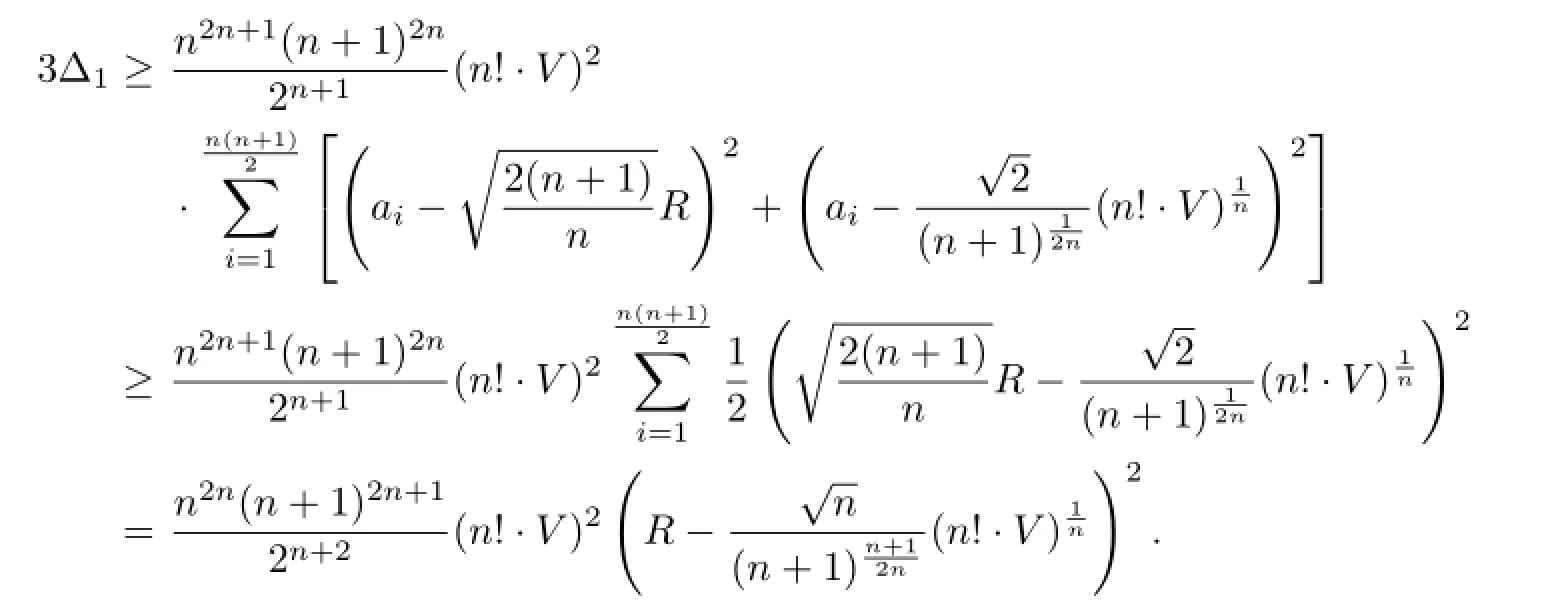
Thus equality(2.1)is valid.From Lemmas 3.1–3.4,it is easy to see that equality holds in (2.1)if and only if Ωnis regular.

The Proof of Theorem 2.2Similar to the proof of Theorem 2.1,by the arithmeticgeometric mean inequality,the inequalities(3.3),(3.4)and(3.5),it follows that

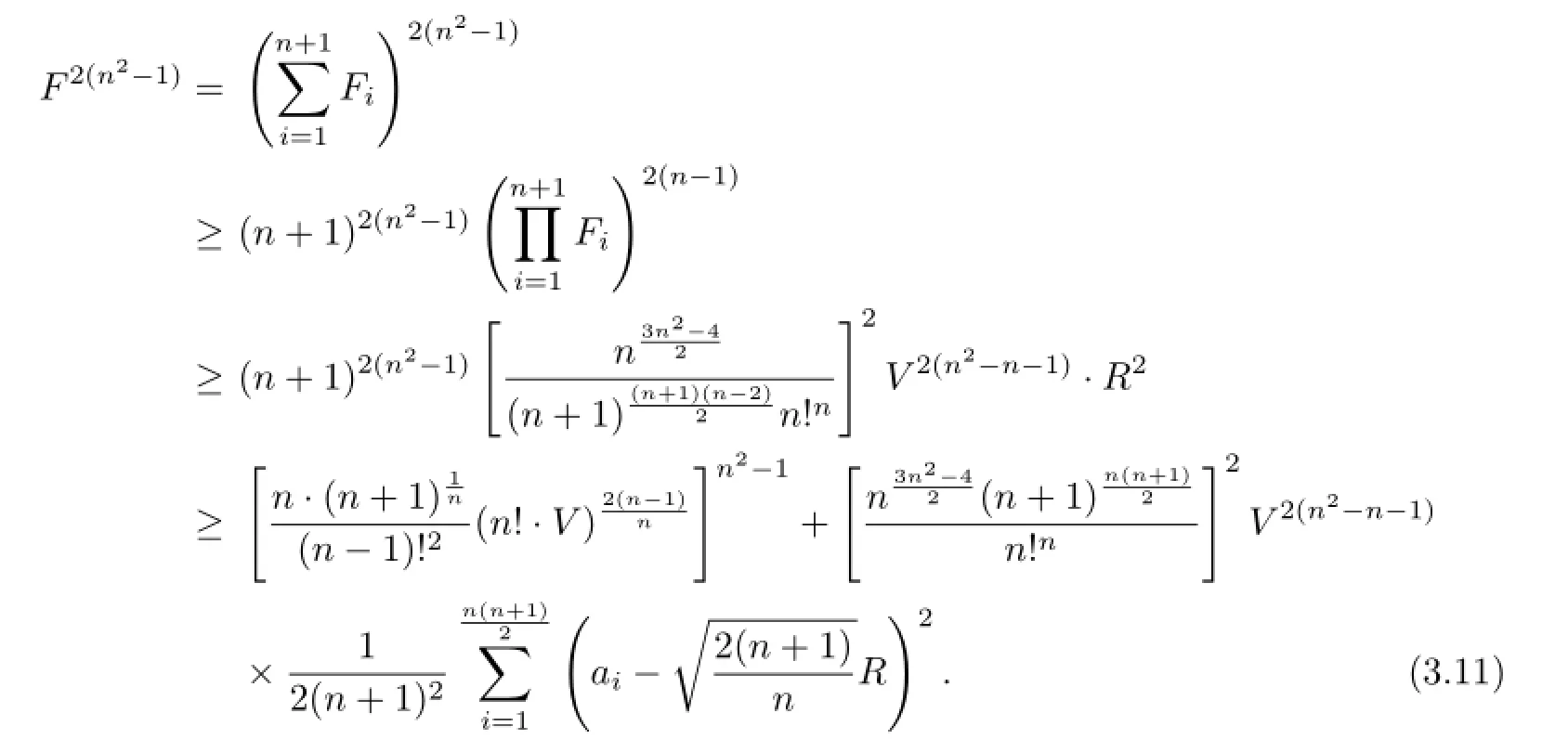
On the other hand,we have

From(3.11)and(3.12),furthermore,applying(3.8),we obtain

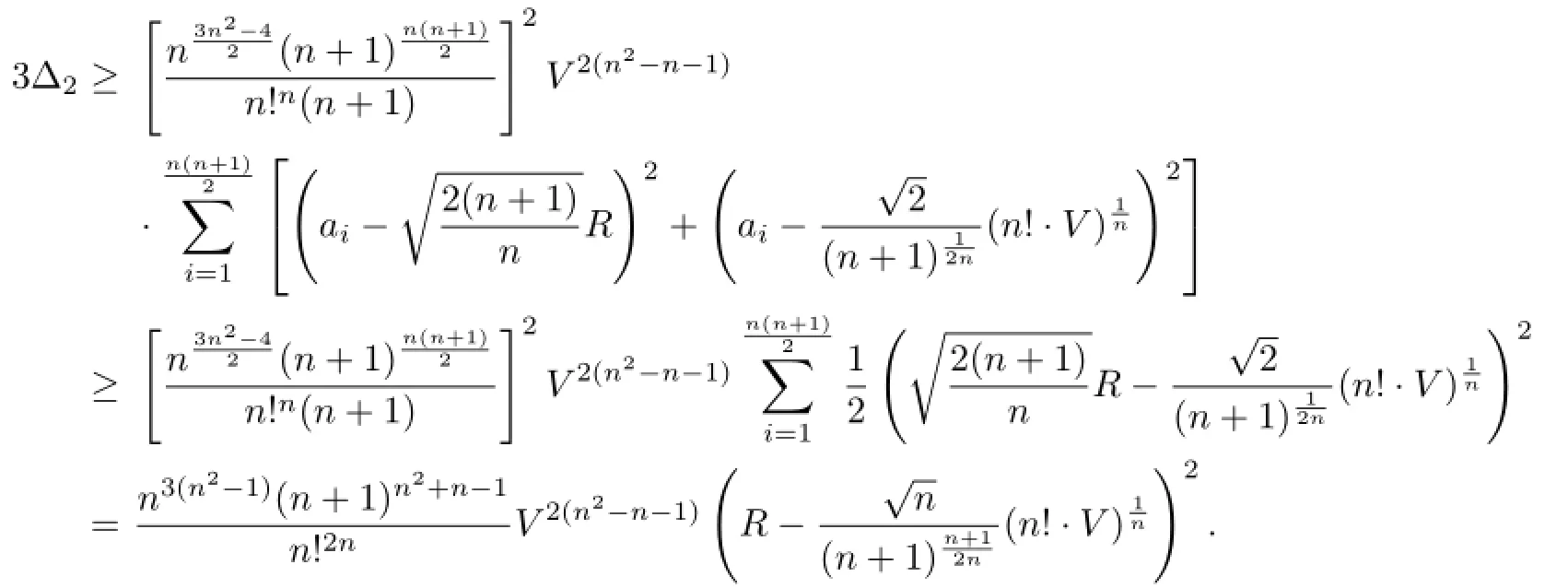
Thus equality(2.2)is true.From Lemmas 3.1–3.4,it is easy to see that equality holds in (2.2)if and only if Ωnis regular.

[1]Osserman R.Bonnesen-style isoperimetric inequalities.Amer.Math.Monthly,1979,86:1–29.

[2]Bokowski J,Heil E.Integral representation of quermassintegrals and Bonnesen-style inequalities.Arch.Math.(Basel),1986,47(1):79–89.

[3]Bonnesen T.Les Probl`ems des Isop´erim`etres et des Is´epiphanes.Paris:Gauthier-Villars,1929.

[4]Bonnesen T,Fenchel W.Theorie der konvexen K¨orper(German).Berichtigter Reprint.Berlin-New York:Springer-Verlag,1974.

[5]Zhou J Z,Xia Y W,Zeng C N.Some new Bonnesen-style inequalities.J.Korean Math.Soc., 2011,48(2):421–430.

[6]Zhang G Y,Zhou J Z.Containment Measures in Integral Geometry.Integral Geometry and Convexity.Hackensack,NJ,:World Sci.Publ.,2006,153–168.

[7]Martini H,Mustafaev Z.Extensions of a Bonnesen-style inequality to Minkowski spaces.Math. Inequal.Appl.,2008,11:739–748.

[8]Cianchi A,Pratelli A.On the isoperimetric defcit in Gauss space.Amer.J.Math.,2011,133(1):131–186.

[9]Figalli A,Maggi F,Pratelli A.A mass transportation approach to quantitative isoperimetric inequalities.Invent.Math.,2010,182(1):167–211.

[10]Zun S.Geometric Inequalities in China(in Chinese).Nanjing:Jiangsu Education Press,1996.

[11]Mitrinovi´c D S,Peˇcari´c J E,Volenec V.Recent Advances in Geometric Inequalities.Mathematics and its Applications(East European Series),vol.28.Dordrecht:Kluwer Academic Publishers Group,1989.

[12]Wang W,Yang S G.On Bonnesen-style isoperimetric inequalities for n-simplices.Math.Inequal.Appl.,2015,18(1):133–144.

A

1674-5647(2017)01-0019-07

10.13447/j.1674-5647.2017.01.03

Received date:April 29,2015.

Foundation item:The Doctoral Programs Foundation(20113401110009)of Education Ministry of China, Universities Natural Science Foundation(KJ2016A310)of Anhui Province.

E-mail address:wenwang1985@163.com(Wang W).

2010 MR subject classifcation:51K05,52A38,52A40