Endpoint Estimates for Commutators of Fractional Integrals Associated to Operators with Heat Kernel Bounds

LIU XIAN-JUN,LI WEN-MING AND YAN XUE-FANG

(College of Mathematics and Information Science,Hebei Normal University, Shijiazhuang,050024)

Endpoint Estimates for Commutators of Fractional Integrals Associated to Operators with Heat Kernel Bounds

LIU XIAN-JUN,LI WEN-MING AND YAN XUE-FANG*

(College of Mathematics and Information Science,Hebei Normal University, Shijiazhuang,050024)

Communicated by Ji You-qing

Let L be the infnitesimal generator of an analytic semigroup on L2(Rn) with pointwise upper bounds on heat kernel,and denote by L−α/2the fractional integrals of L.For a BMO function b(x),we show a weak type LlogL estimate of the commutators[b,L−α/2](f)(x)=b(x)L−α/2(f)(x)−L−α/2(bf)(x).We give applications to large classes of diferential operators such as the Schr¨odinger operators and second-order elliptic operators of divergence form.

fractional integral,commutator,LlogL estimate,semigroup,sharp maximal function

1 Introduction and Main Results

Suppose that L is a linear operator on L2(Rn)which generates an analytic semigroup e−tLwith a kernel at(x,y)satisfying an upper bound of the form

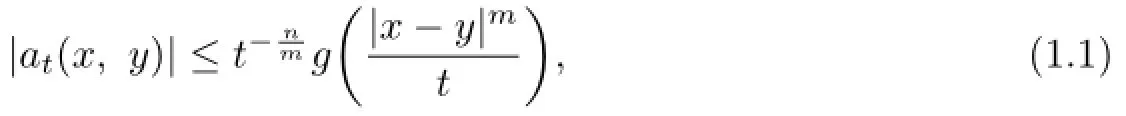
where m is a positive fxed constant and g is a positive,bounded,decreasing function satisfying

for some ε＞0.

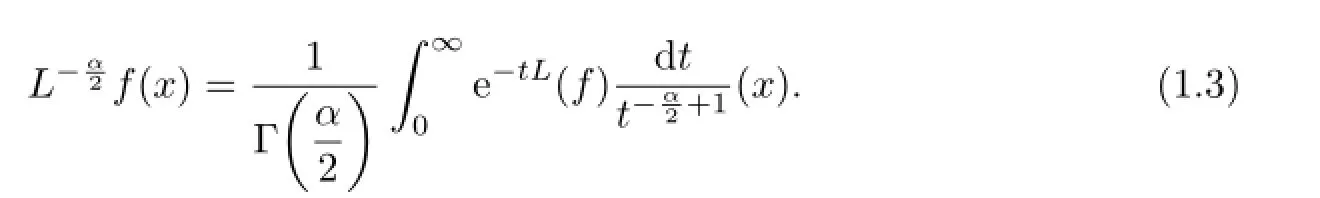
Note that if L=−∆is the Laplacian onRn,thenis the classical fractional integrals

Iα(see,for example,Chapter 5 in[1]),

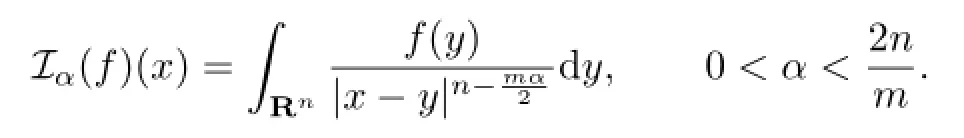
Let b be a BMO function onRn.The commutator of b andis defned by

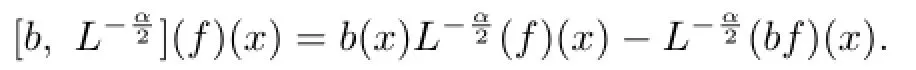
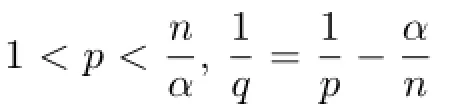
The aim of this paper is to prove the following estimate.

Theorem 1.1Let b∈BMO,Φ(t)=t(1+log+t).Then for every 0＜α＜,and

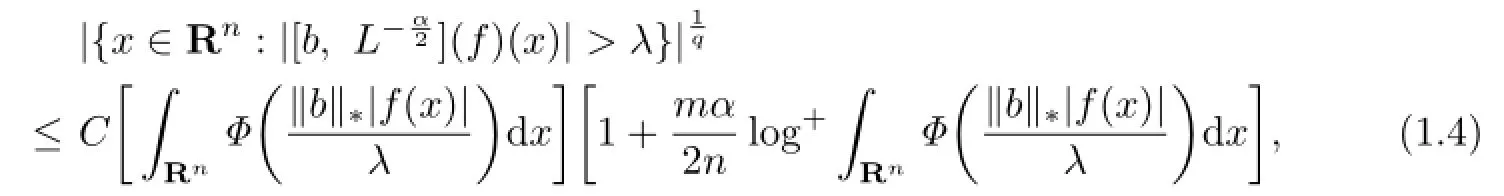
where‖b‖∗denotes the BMO norm of b(x).

Our result extends the results of[3]and[4]from(−∆)to a general operator L,while we only assumes pointwise upper bounds on kernel at(x,y)of e−tLand no regularity on its space variables.Under our assumptions,the kernel of the operatordoes not have any regularity on space variables x and y.This allows fexibility on the choice of operator L in applications.

The paper is organized as follows.In Section 2,we recall some important estimates on BMO functions,maximal functions and fractional integrals.In Section 3,we prove some estimates on fractional integrals,which play a key role in the proof of the main result Theorem 1.1,which will be shown in Section 4 by using the approach of[4]and[7],combining with some estimates on the sharp maximal function.We conclude this paper by giving applications to large classes of diferential operators which include the Schr¨odinger operators and second-order elliptic operators of divergence form.

Throughout,the letter“C”denote(possibly diferent)constants that are independent of the essential variables.

2 Defnitions and Preliminary Results

Denote the Hardy-Littlewood maximal function Mf and its variant Mαf by

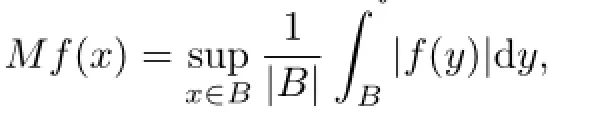
and

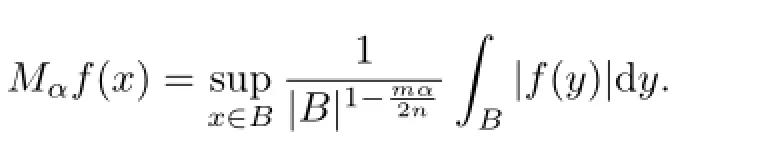
For any f∈Lp(Rn),p≥1,the sharp maximal functionassociated with“generalized approximations to the identity”{e−tL,t＞0},is given by

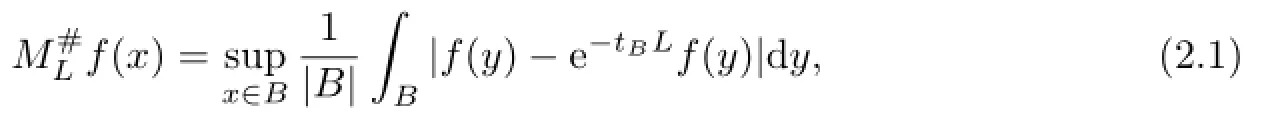
where tB=and rBis the radius of the ball B(see[8]).

A function A:[0,∞)→[0,∞)is said to be a Young function if it is continuous,convex, and increasing satisfying A(0)=0,A(t)→+∞as t→+∞.We defne the A-average of a function f over a ball B by means of the following Luxemburg norm:

For the mean Luxemburg norm,the following generalized H¨older inequality holds(see[9]):

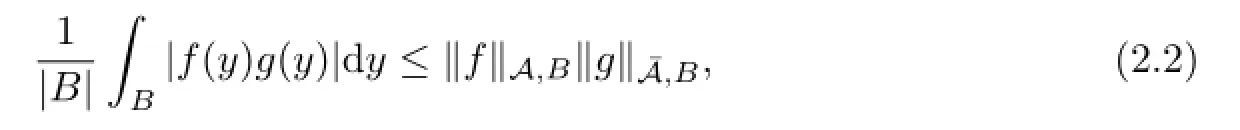
We use a Young function Φ(t)=t(1+log+t)with the corresponding average denoted by‖f‖Φ,B=‖f‖LlogL,B.Its complementary Young function is(t)≈etwith the corresponding average denoted by‖f‖¯Φ,B=‖f‖expL,B.We also introduce the maximal operator of the fractional order associated with‖·‖LlogL,B,which is defned by

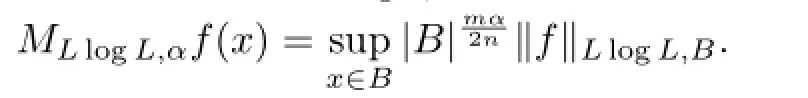
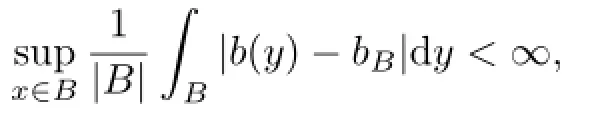
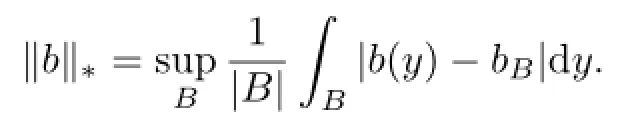
Lemma 2.1(i)Assume that b∈BMO and N＞1.Then for every ball B,we have

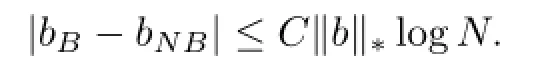
(ii)(John-Nirenberg Lemma)Let 1≤p＜∞.Then b∈BMO if and only if

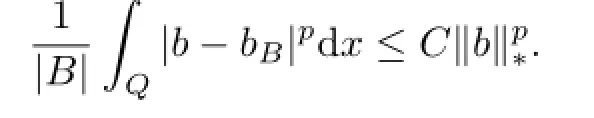
(iii)If b∈BMO,then there exists a constant C such that for every ball B,

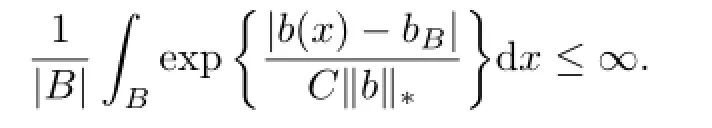
(iv)For every p∈[1,∞],there exists a constant C such that for every f∈Lp,

Proof. For the proofs of(i)and(ii),see Lemma 2.1 of[7].For(iii),see Chapter 6 of[10], and for(iv),see Proposition 2.4 of[11].

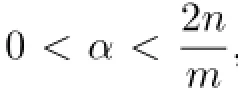
(i)There exists a constant C such that for any ball B,

(ii)Iαf∈A1;in particular,it satisfes the reverse H¨older inequality for some exponent r＞1.

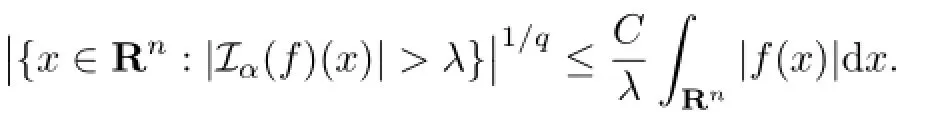
(iv)If Mf is locally integrable,then there exists a constant C independent of f and x such that

Proof. For the proofs of(i)–(iii),see Lemma 5.2 of[4].For(iv),see Lemma 2.3 of[3].

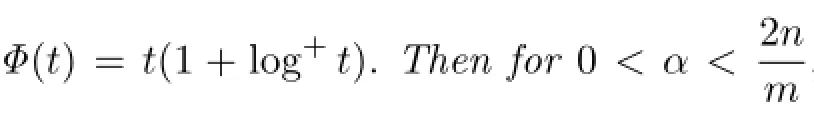
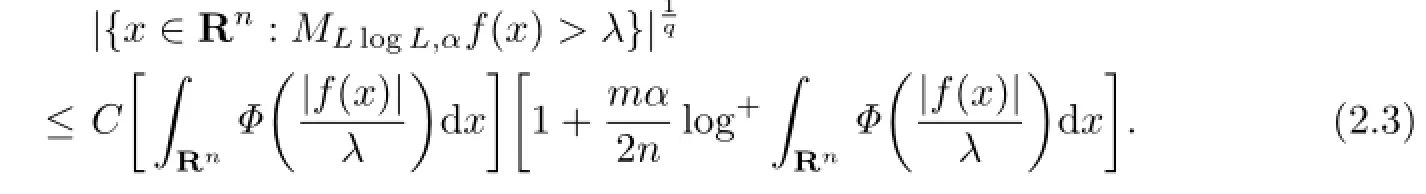
Proof. For the proof of this lemma,see Lemma 2.7 of[3].

In the end of this section,we state the following analogue of the Feferman-Stein inequality on the sharp maximal function

Lemma 2.4Let λ＞0 and f∈Lp(Rn)for some 1＜p＜∞.Then for every 0＜η＜1, we can fnd γ＞0 independent of λ,f in such a way that

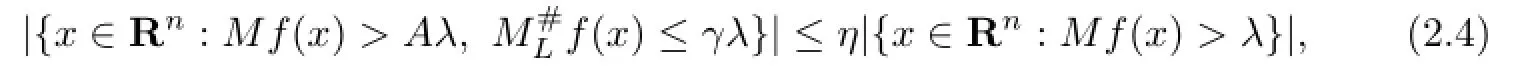
where A＞1 is a fxed constant which depends only on n.

As a consequence,we have the following estimate:

(ii)Let φ:(0,∞)→(0,∞)be a doubling function.Then,for any positive constant q, there exists a positive constant c=c(q)such that

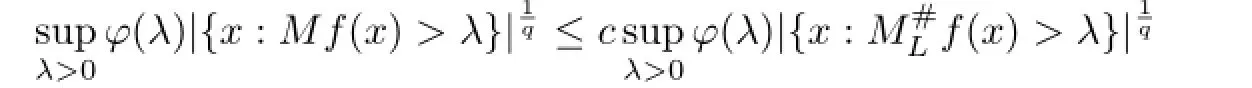
for all functions f such that the left side is fnite.

Proof. For the proof of(2.4),we refer to Proposition 4.1 of[8].

3 Some Estimates on Fractional Integrals

In this section,we prove several lemmas on fractional integralswhich will play a key role in the proof of Theorem 1.1.

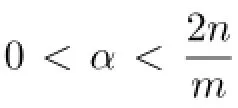
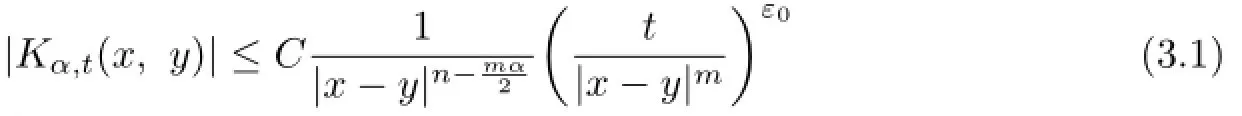
Proof. Note that

Hence,by(1.3),

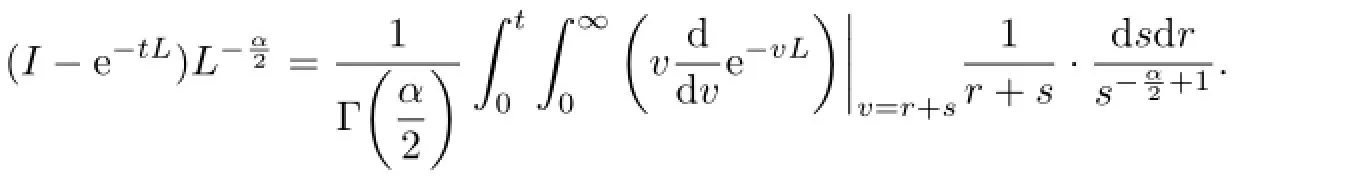
an associated kernel Kα,t(x,y)which satisfes

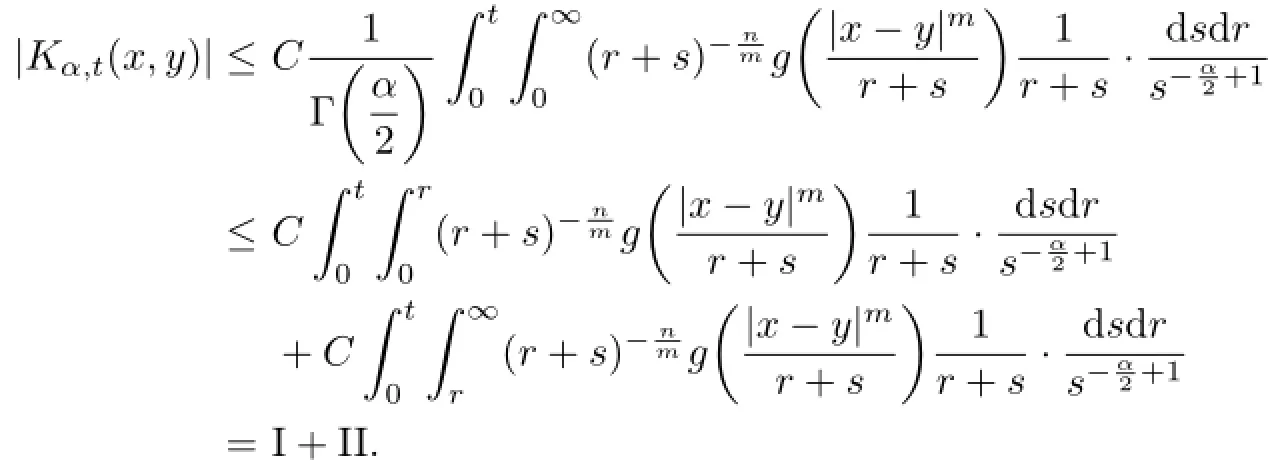
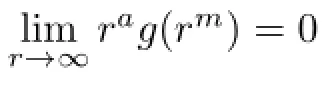
Let us estimate term I.Note that 0＜s＜r,one has

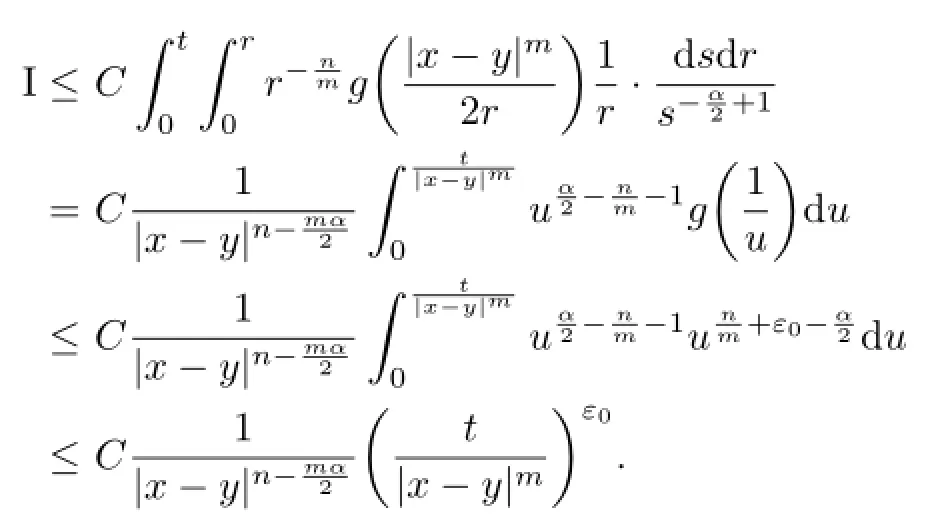
For II,note that 0＜r＜s,one has

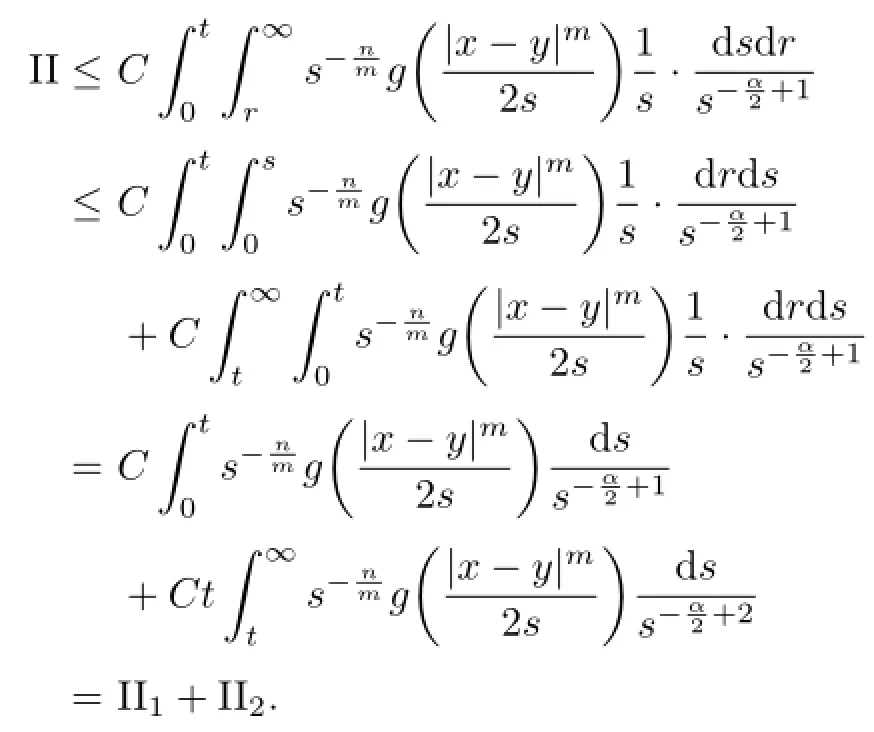
Similar to the estimate of term I,one has

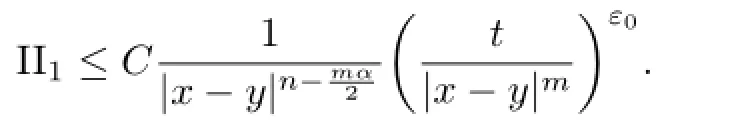
On the other hand,

Therefore,condition(3.1)is satisfed and then the proof of Lemma 3.1 is completed.

We remark that when L has a Gaussian upper bounds,Lemma 3.1 is proved in[7]for 0＜α＜1,and in[13]for 0＜α＜n,respectively.

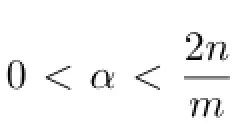
for some positive constant C.

Lemma 3.2Let b∈BMO.Then there exists a positive constant C such that

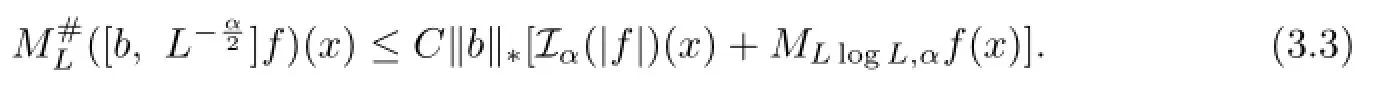
Proof. Since Iαf∈A1,it sufces to prove that there exists a constant C such that for all x∈Rnand for all B∋x,

where tB=,and rBis the radius of B.

For an arbitrary fxed x∈Rn,choose a ball B=B(x0;r)={y∈Rn:|x0−y|＜r} which contains x.Let f1=fχ2Band f2=f−f1.One writes

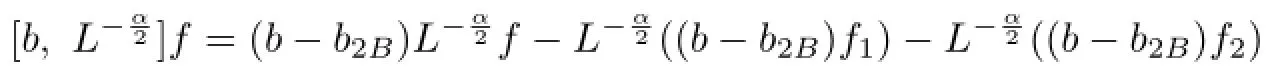
and

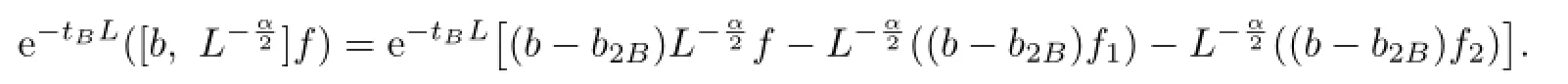
Then,

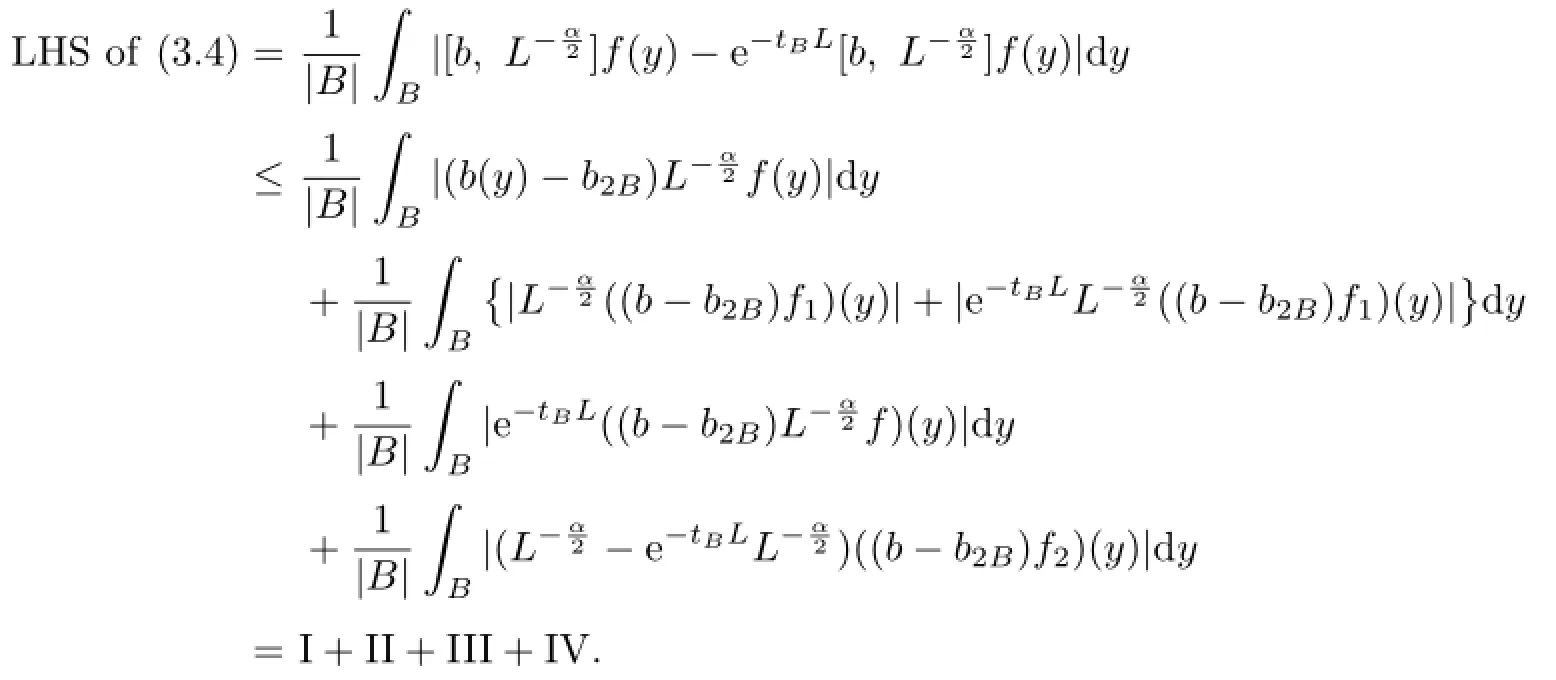
We estimate each integral in turn.Obviously,by(3.2),we have the following pointwise inequality

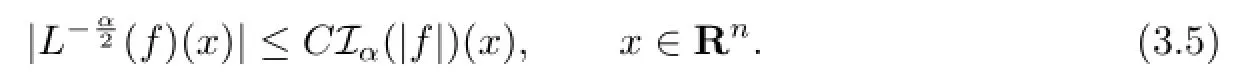
For I,by Lemma 2.2,Iαf satisfes the reverse H¨older’s inequality with exponent r,by Lemma 2.2 and(3.5),we have

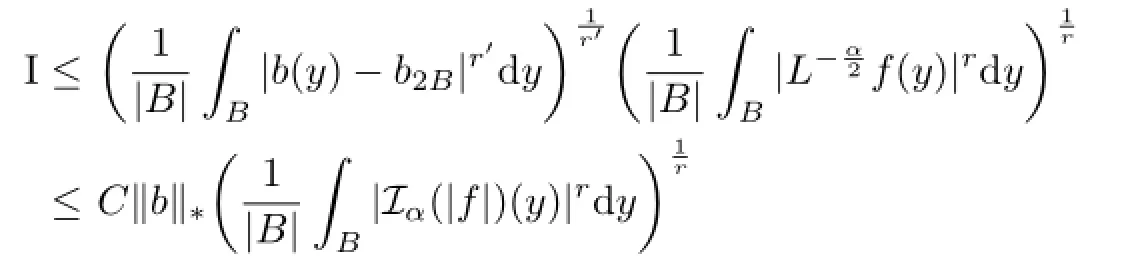
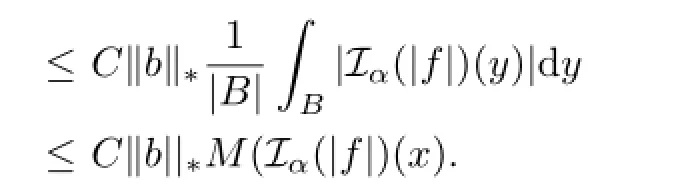
To estimate the second integral,note that by Lemmas 2.1,2.2 and(3.5),

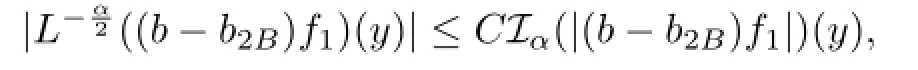
and

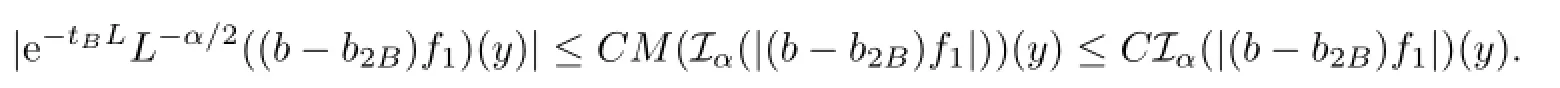
Hence,by Lemmas 2.2,2.1,and by the generalized H¨older’s inequality(2.2),

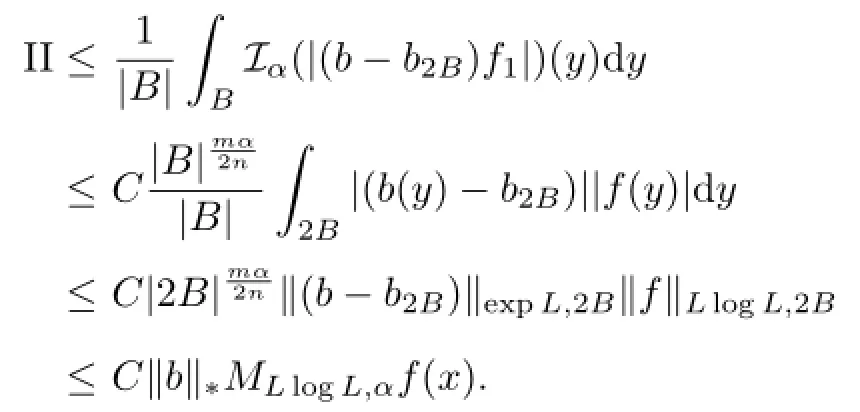
For term III,we have

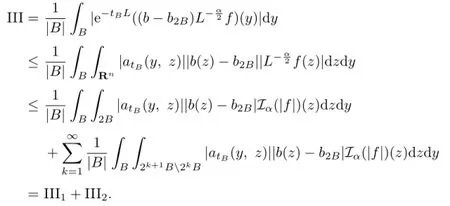
We now estimate III1.For y∈B,z∈2B,we have

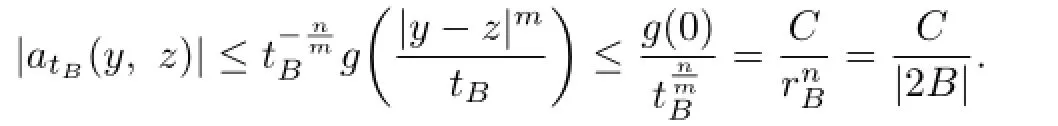
Similar to the estimate of term I,we obtain

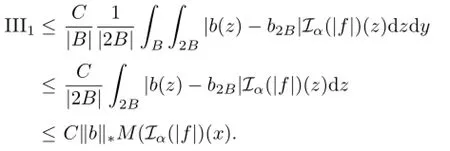
Regarding III2,for y∈B and z∈2k+1B2kB,we have

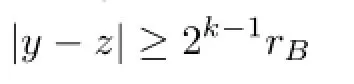
and

Similarly,by Lemma 2.1,we have

Let us see what happens with term IV.By using Lemmas 3.1 and 2.1,one has

Combining the above estimates I,II,III and IV,we obtain(3.4),and the proof of Lemma 3.2 is completed.

4 Proof of Theorem 1.1

(i) By Lemmas 2.4,3.2 and 2.2,we have

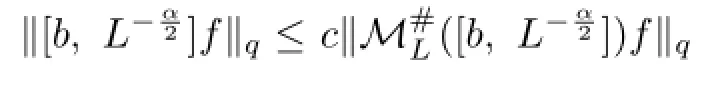
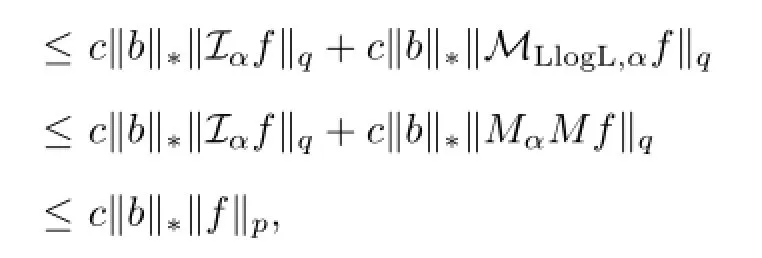
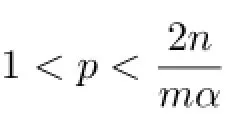
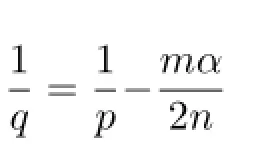
(ii) Without loss of generality,we assume that f is a smooth function with compact support.By homogeneity,it sufces to verify that(1.4)is true for λ=1,that is,

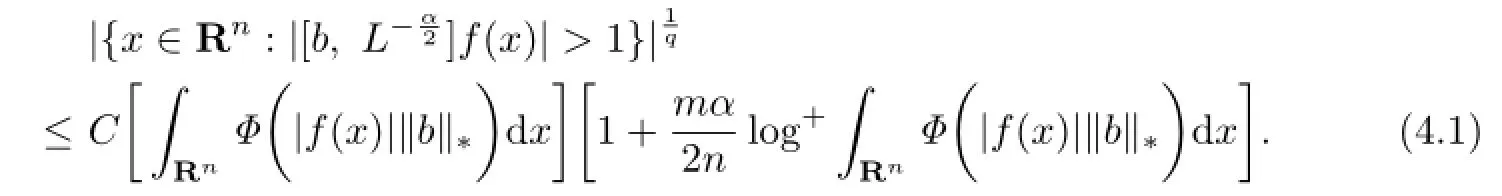
Note that

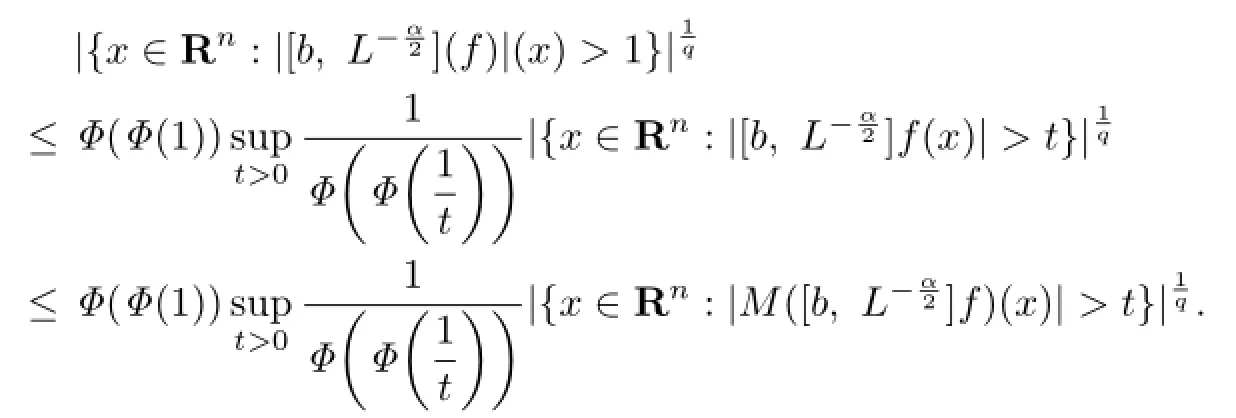
Let

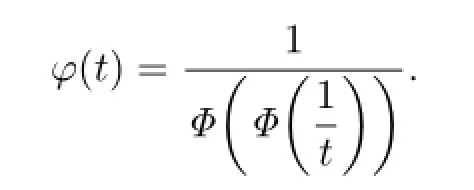
A straightforward calculation shows that φ(t)is a doubling function.So

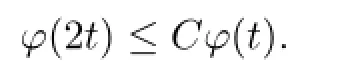
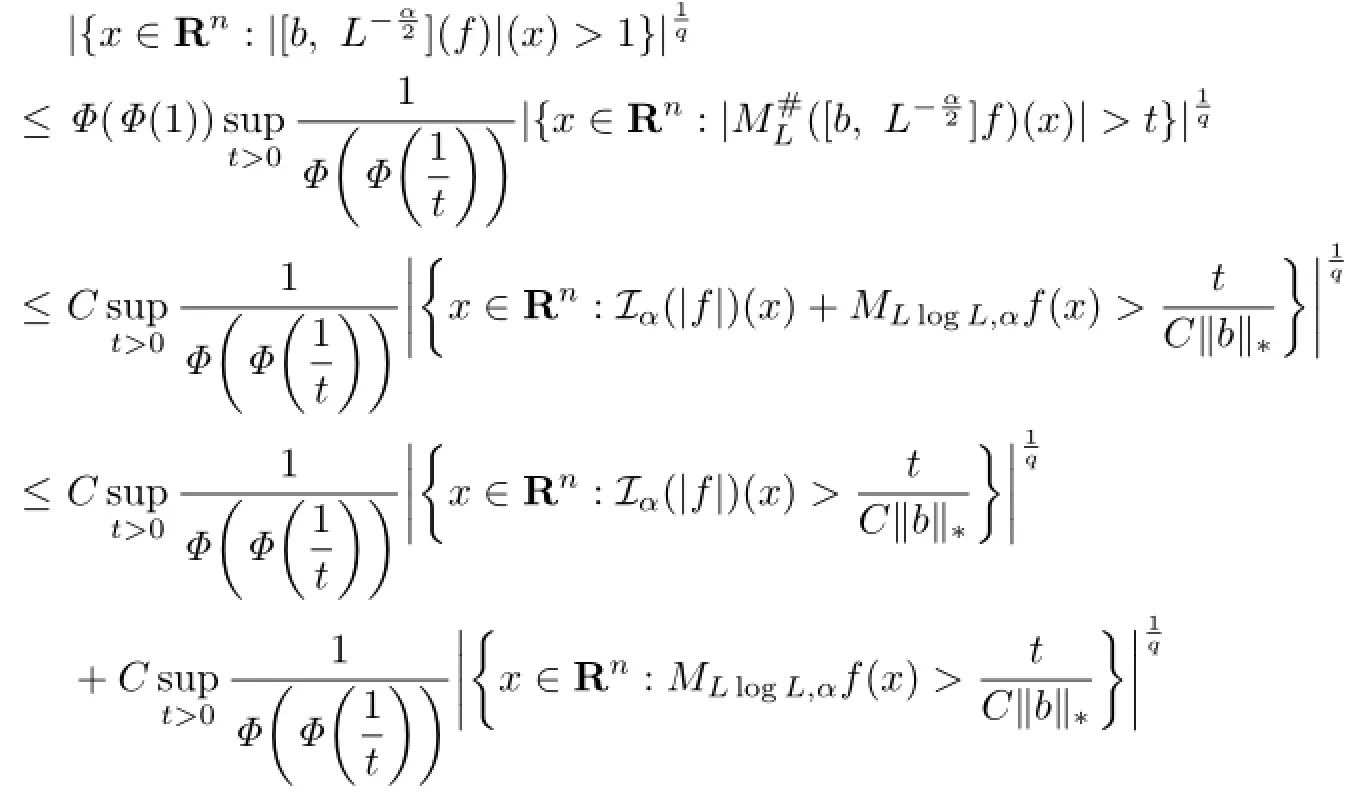
Furthermore,since t≤Φ(t),we have

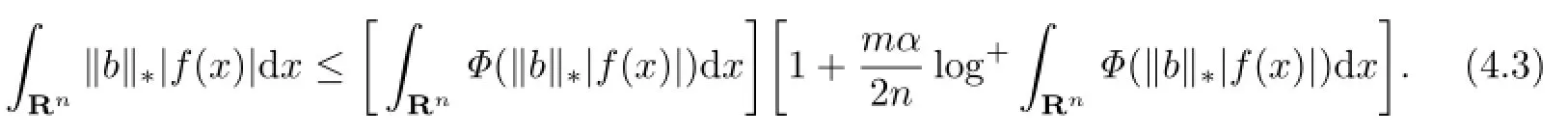
From(4.2)and(4.3)we get

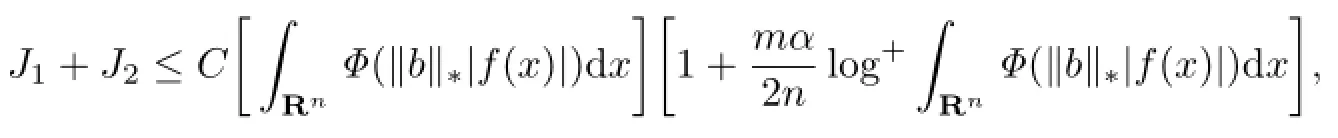
which proves(4.1).The proof of Theorem 1.1 is completed.

Remark 4.1The heat kernel upper bound(1.1)of Theorem 1.1 is satisfed by large classes of diferential operators.We list some of them as follows.

(a)Let V be a nonnegative function onRn.The Schr¨odinger operator with potential V is defned by

By domination,the kernel at(x,y)of the semigroup{e−tL}t＞0has a Gaussian upper bound(see[14]).Therefore,the result for the fractional integrals,that is Theorem 1.1, holds for the operator L of(4.4)in which V is a nonnegative function onRn.

Note that unless V satisfes additional conditions,the heat kernel can be a discontinuous function of the space variables and the H¨older continuous estimates may fail to hold.

(b)Let A=((aij(x))1≤i,j≤nbe an n×n matrix of complex with entries aij∈L∞(Rn) satisfying

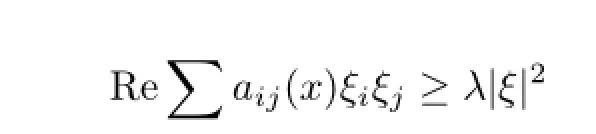
for all x∈Rn,ξ=(ξ1,ξ2,···,ξn)∈Cnand some λ＞0.We defne a divergence form operator

which we interpret in the usual weak sense via a sesquilinear form.

It is known that the Gaussian upper bound on the heat kernel e−tLis true when A has real entries,when n=1,2 in the case of complex entries,see Chapter 1 of[15].

[1]Stein E M.Singular Integral and Diferentiability Properties of Functions.Princeton:Princeton Univ.Press,1970.

[2]Chanillo S.A note on commutators.Indiana Univ.Math.J.,1982,31:7–16.

[3]Ding Y,Lu S Z,Zhang P.Weak estimates for commutators of fractional integral operators. Sci.China Ser.A,2001,44:877–888.

[4]Cruz-Uribe D SFO,Fiorenza A.Endpoint estimates and weighted norm inequalities for commutators of fractional integrals.Publ.Mat.,2003,47(1):103–131.

[5]Bramanti M,Cerutti M.Commutators of singular integrals and fractional integrals on homogeneous spaces.Contemp.Math.,1995,189:81–94.

[6]Hu G E,Meng Y,Yang D C.Multilinear commutators for fractional integrals in nonhomogeneous spaces.Publ.Mat.,2004,48:335–367.

[7]Duong X T,Yan L X.On commutators of fractional integrals.Proc.Amer.Math.Soc.,2004,132:3549–3557.

[8]Martell J M.Sharp maximal functions associated with approximations of the identity in spaces of homogeneous type and applications.Studia Math.,2004,161:113–145.

[9]Per´ez C.Endpoint estimates for commutators of singular integral operators.J.Funct.Analysis, 1995,128:163–185.

[10]Duoandikoetxea J.Fourier Analysis.in:Humphreys J(chair),Saltman D,Sattinger D,Stern R ed.Grad.Studies Math.29,Amer.Math.Soc.,Providence,Rhode Island,2000.

[11]Duong X T,Robinson D W.Semigroup kernels,Poisson bounds,and holomorphic functional calculus.J.Funct.Anal.,1996,142:89–128.

[12]Duong X T,Yan L X.Duality of Hardy spaces associated with operators with heat kernel bounds.J.Amer.Math.Soc.,2005,18:943–973.

[13]Deng D G,Duong X T,Sikora A,Yan L X.Comparison of the classic BMO with the BMO spaces associated with operators and applications.Rev.Mat.Iberoamericana,2008,24:267–296.

[14]Davies E B.Heat Kernels and Spectral Theory.Cambridge:Cambridge Univ.Press,1989.

[15]Auscher P,Tchamitchian P.Square root problem for divergence operators and related topics. Asterisque,1998,249.Soc.Math.France.30–31.

A

1674-5647(2017)01-0073-12

10.13447/j.1674-5647.2017.01.08

Received date:May 17,2016.

Foundation item:The Science and Technology Research(Z2014057)of Higher Education in Hebei Province, the Doctoral Foundation(L2015B05)of Hebei Normal University,and the NSF(A2015403040)of Hebei Province.

*Corresponding author.

E-mail address:liuxianjun@126.com(Liu X J),yanxuefang2008@163.com(Yan X F).

2010 MR subject classifcation:42B20,42B25,47B38