层次拓扑空间范畴及其刻画
2017-02-05高珺超吴修云
高珺超 曾 港 崔 港 梁 菲 吴修云
高珺超曾港崔港梁菲吴修云
(湖南科技学院 理学院,湖南 永州 425199)
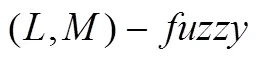

1 引 言

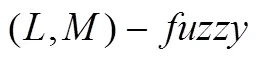
拓扑空间是一门模糊化拓扑空间,它是一般拓扑空间、M-fuzzifying拓扑空间、拓扑空间等概念的统一的推广形式,因而它是具有较高的概括性。目前,拓扑空间理论得到了较完善的发展[12-14]。但拓扑空间的层次理论至今还没得到讨论和发展。因此,本文中,我们引入层次拓扑空间,给出它与层次拓扑空间的关系,并给出了层次保序算子空间范畴的几种等价刻画,其中包括层次邻域空间范畴、层次闭包空间范畴以及层次内部空间范畴。
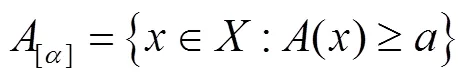


,。
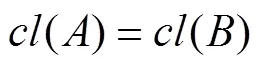
;

;

,
证明:直接利用定义可证。
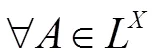
,。

。

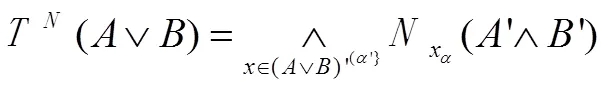
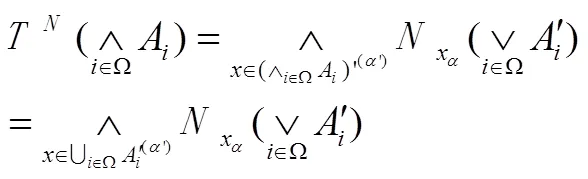

。

。
证明:此证明与定理3.4和定理3.6类似。
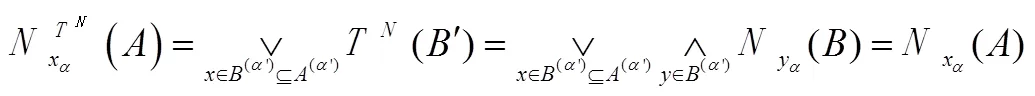
。
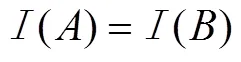
;

。

。
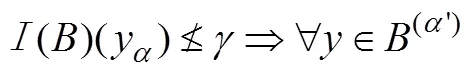
,

。
充分性。我们先验证

。

。
最后,我们验证

。



证明:根据定义,
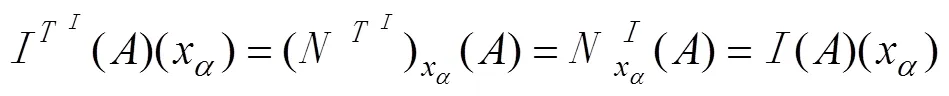

, ,。

,,。

。
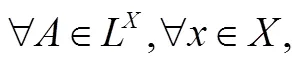
。
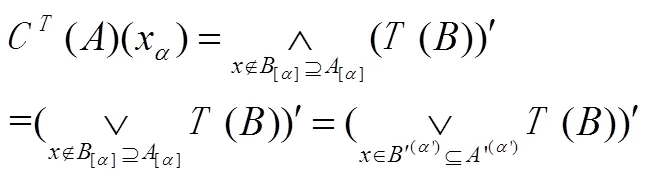

,,。
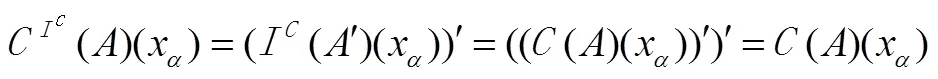
。

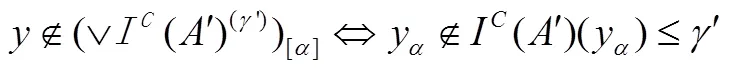

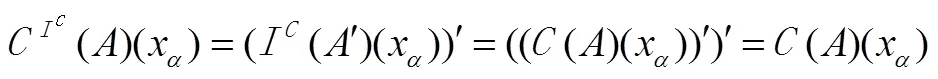
。

。
证明:由定理4.7,5.4,5.7和5.9,

。
[12]U.Hohle,S.E.Rodabaugh.Mathematics of Fuzzy sets:Logic,Topology,and Measure Theory[M],Boston,Dordrecht, London:Kluwer Academic Publishers,1999.
(责任编校:宫彦军)
2016-12-26
湖南教育厅研究项目资助(项目编号15C0586);湖南科技学院重点学科建设项目资助;湖南科技学院科技文化节项目资助。
高珺超(1991-),女,湖南科技学院数学与应用数学专业学生。
吴修云(1982-),男,安徽六安人,副教授,博士,研究方向为格上拓扑学、模糊凸结构。曾港(男),崔港(男),梁菲(女),湖南科技学院理学院学生。
O189
A
1673-2219(2017)10-0005-05
