浅析初中数学教学中的全等三角形解题策略

谢瑶谋

摘 要：全等三角形的内容是初二数学中的重点知识，也是教学中的难点。许多学生由于基础知识薄弱或无法进行逻辑推理等原因，造成了在学习中遇到重重障碍的困境，致使全等三角形的教学工作难以有实质性的跨域，针对这些实践中出现的问题提出了几点解题策略，望对各位同仁有所裨益。

关键词：中学数学；全等三角形；解题策略

全等三角形这类题目在考试中多以大题形式出现，要求证明两三角形全等或根据已知的三角形求另一三角形的某个边长，这样的大题若失分则成绩难以提高，因此，在初中教学中，数学教师应当将此问题重视起来。

一、全等三角形在实践解题中出现的问题

1.基础概念掌握不牢固

所谓全等三角形是指经过翻转、平移后，能够完全重合的两个三角形叫做全等三角形，而该两个三角形的三条边及三个角都对应相等。验证两个全等三角形一般用边边边（SSS）、边角边（SAS）、角边角（ASA）、角角边（AAS）和直角三角形的斜边，直角边（HL）来判定。有些初中生在学习全等三角形时，认为概念类的知识根本用不着记忆，只要在实践中多加练习自然就能明白，因此，忽略了概念的重要性。在证明两个三角形全等的过程中根本不清楚需要用到哪些条件，如此，怎能学好全等三角形知识。

2.思路不清，逻辑混乱

证明两个三角形全等的过程，是逻辑推理、分析、整合的过程，如果在大脑中不能形成一个严密的逻辑推理程序是无法解决三角形全等问题的。这一点具体体现在，有些学生不清楚要证明A问题需要先证明B还是先证明C，或者是将B和C证明出来后，又如何与A产生联系，这种思路不清、逻辑混乱的现象成了学习全等三角形知识的绊脚石。

3.思维固定，无法举一反三

在教学实践中，有很多学生出现过类似的现象，教师教给一种方法后，在学生的脑海中形成了固定的思维模式，当题目换了另外一个说法后，学生就无法理解其中的意思了，当然在解题时也就会显得很慌乱。

二、关于全等三角形的解题策略

在解决数学三角形全等的相关问题时，教师首先要教导学生将基础性的概念牢牢掌握，因为只有在充分理解概念的基础上才能实现证明、计算的过程，否则，无异于空谈。其次，是培养学生严密的逻辑推理能力，理清思路，不管要证明的图形样式有多么复杂，唯记住一点万变不离其宗，一定要找到自己所要求的三角形。最后是教导学生要做到活学活用，培养学生一题多解的能力，通过多种渠道达到求解的目的。以下笔者将举出几个经典解题方法，简要分析。

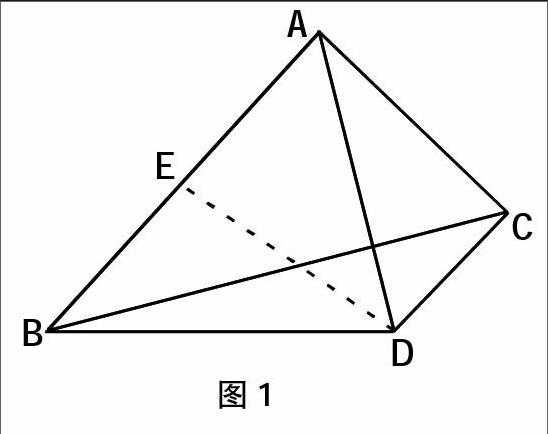
1.如图1，已知△ABC中，AB=2AC，∠BAD=∠CAD，DA=DB，求证：DC⊥AC。

解题思路：如图1，在AB线段上取一中点E，因为AD=BD，AE=BE，DE=DE，所以，△ADE≌△BDE，所以，∠BED=∠AED=90°，又因为，AB=2AC，所以，AC=AE，∠DAB=∠CAD，AD=AD，所以，△AED≌△ACD，所以，∠ACD=∠AED=90°，所以DC⊥AC。这道题中，是典型的中线法证明求解过程，通过连接中点和顶点的方法构造出两个全等的三角形，并以公共边为突破点实现证明求解的目的。对于学生来说，只要能想到做辅助线ED，基本就可以达到求解的目的了。所以，在实践教学中，教师应当教导学生学会做必要的辅助线来求解。

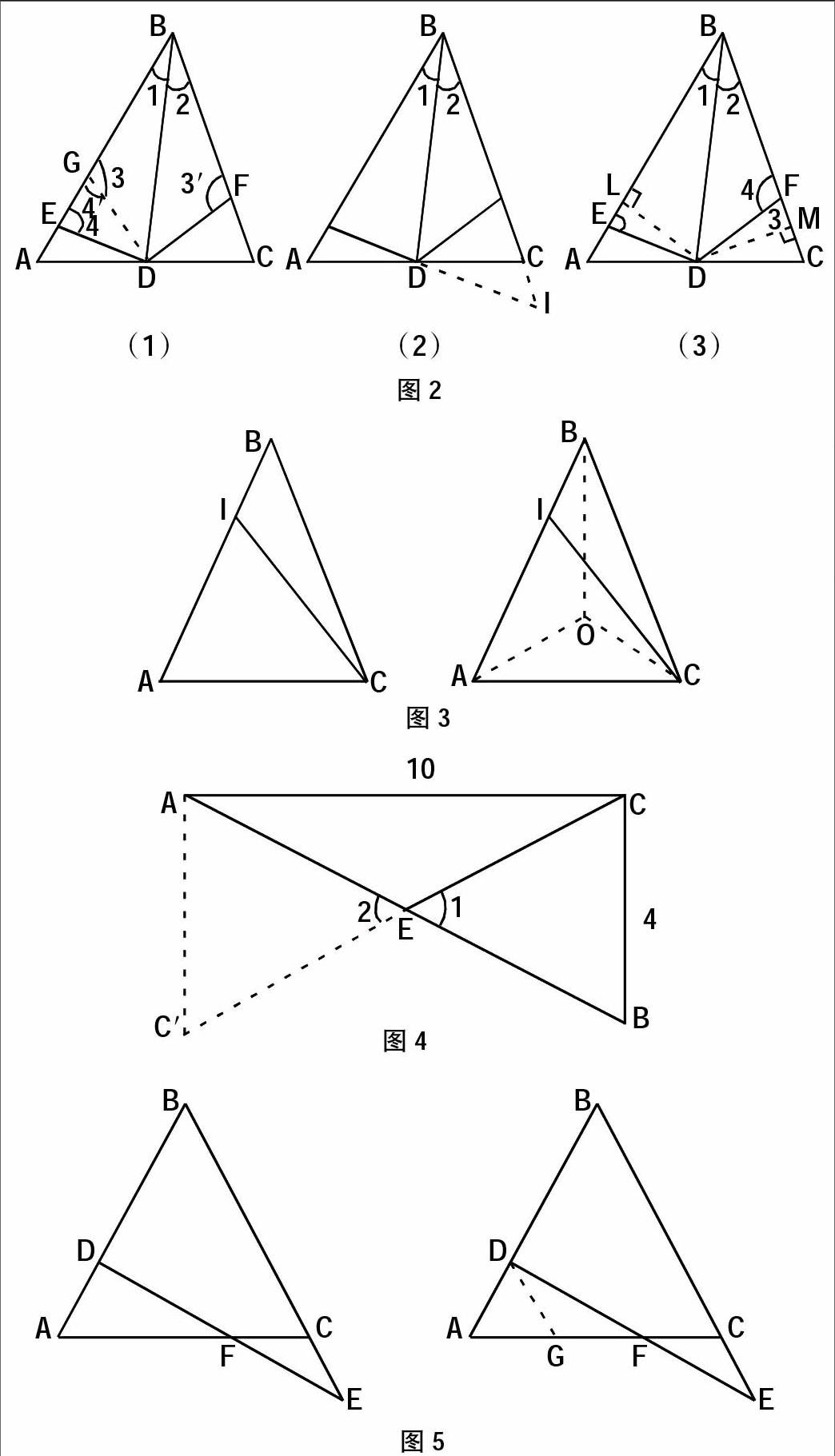
2.见图2，在△ABC中，线段BD平分∠ABC，点E、F分别是AB、BC边上的一点，∠EDF+∠EBF=180°。求证：DF=DE。

这道题可以有三种方法来解，分别是：截长法、补短法和以“角平分线上的点到角的两边距离相等”这一法则来证明DF=

DE。限于篇幅原因，第二种和第三种本文只给出相应的图示，以下具体讲解第一种方法。

截长法解题思路：如图，在线段AB上取一点G，可得BG=BF，由此可知，△BDF≌△BDG，所以，DG=DF，又因为，∠EDF+∠EBF=180°，所以，在四边形BEDF中∠4+∠3′=180°，∠4′+∠3=180°，∠3′=∠3，所以，∠4=∠4′，所以，△DEG是等腰三角形，所以DG=DE，又因为DF=DG，所以，DF=DE。这道题是通过将原有的线段经过截断，达到与另一个三角形实现全等的解题过程，进而使问题得到解决，另外，此题还涉及了四边形的内角和与等腰三角形的知识点，对于中学生来说又是一次知识的提高。

3.在图3中，△ABC的∠ABC=20°，AB=BC，BI=AC，则求解

∠AIC的度数。

解题思路：如图3，以AC为边向△ABC内部做等边三角形AOC，可知∠BAO=∠BCO=∠ABC=20°，AC=AO=CO=BI，AB=BC，所以，△BIC≌△BOA≌△BOC，所以，∠BOA=∠BOC，所以，∠BOA+∠BOC+∠AOC=360°，所以∠BOA=∠BOC=∠BIC=150°，所以∠AIC=180°-150°=30°。这一种典型的从被求解的三角形内部再次构建特殊三角形以达到证明三角形全等的求解方式，在全等三角形解题实践中也是较为常用的一种，教师要教导学生在答题时灵活运用此方法。

4.已知△ABC的两条边AC=10，BC=4，那么，第三条边上的中线长m的取值范围是（ ）。

解题思路：如图4，只要将题意理解透彻，并快速在脑中能构建出相应的全等三角形，将要求解的问题转化到一个待定的三角形中就可以轻松解决了。在图4中原本是没有△ACE部分的，这是为了实现解题添加的必要性辅助线，教师在讲解此类题目时，必须教导学生在做题前将必要的辅助线段在图上画出来，便于理解题目，审清题意。如图4，延长CE至CC′使EC′=EC，进而很容易得到△CBE≌△C′AE，所以，AC′=CB，在△C′AC中，10-4

5.这一点，主要讲的是在解题中利用平行线来构造出两个全等三角形，进而实现解题的方法。如图5，在△ABC中，∠A=∠C，D是线段AB上的一点，AD=EC，求证：DF=FE

解题思路：如图5，做线段DG∥BC并与AC交于点G，所以∠FDG=∠FEC，∠DGF=∠FCE，∠BCA=∠DGA，又因为∠BCA=∠A，所以，∠A=∠DGA，所以DA=DG，又因为CE=DA，所以DG=CE，所以△DGF≌△ECF，所以DF=FE。在这道题中，通过做平行于BC的平行线DG，继而使相对较散的结论集中起来，使要求解的问题降低了难度，在实践中要好好把握这一解题策略。

总而言之，全等三角形的知识点在初中数学测试和考查中占据着重要的地位，教师应予以重视并开展重点教学，积极运用以上几点实践策略对数学教学质量的提高能起到很好的帮助作用。除此之外，数学教师还要肩负起培养全面社会型人才的重担，为国家实现“科教兴国”伟大目标贡献一份力量。

参考文献：

[1]聂亚晶.浅析初中三角形全等教学策略与技巧[J].新课程（中学），2016（1）.

[2]吴光华.初中数学教学中最近发展区的确定及利用策略：以“三角形全等”知识教学为例[J].数学教学通讯，2014（4）.

[3]吴玉龙.初中数学证明题常见的几种解题错误与纠错办法：以“全等三角形”的教学为例[J].语数外学习（初中版上旬），2014（7）.