改进的Dijkstra算法在应急救援最优路径问题中的应用

曹舒淮 王潇 姜浩然 梁宵 曲芳

摘 要：本文目的于寻求最优（时间最短）的资源配送路径。建立时间最短的应急资源调度最优路径选择优化模型，并在考虑距离的基础上同时考虑快速通过的能力。采用最优化方法进行求解，获得最优方案。针对数值实例进行仿真实验，并针对获得的结果进行分析与讨论。

关键词：突发事件；应急救援；最优路径；Dijstra算法

DOI：10.16640/j.cnki.37-1222/t.2017.01.126

Dijkstra算法是经典的最短路算法，是由荷兰计算机科学家狄克斯特拉于1959 年提出的，因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法，解决的是有向图中最短路径问题。迪杰斯特拉算法主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止[1-3]。

1 数值实例

假设J市突然发生自然灾害事件，S市派出人员及物资赶去救援，图1为S市到J市的交通运输示意图，v1为S市，v6为J市，v2、v3、v4、v5为途中主要城市。图中两点间数字代表得出的路径权值（仅考虑距离上的最短）。

2 考虑距离及道路快速通过能力的应用

假设考虑道路快速通过的能力（综合考虑道路等级、路面质量、交通流量、车辆限制、气象条件、实时路况等），可以用系数0.5-1区间值来表示快速通过的能力，具体难易程度如下表1所示。

各路径具体系数：v1-v2系数为0.8，v1-v4系数为0.5，v1-v5系数为0.5，v2-v3系数为0.7，v2-v4系数为0.5，v3-v6系数为0.9，v3-v5系数为0.6，v4-v3系数为0.7，v4-v5系数0.6，v4-v6系数为0.7，v5-v6系数为0.8，得到如下表2所示。

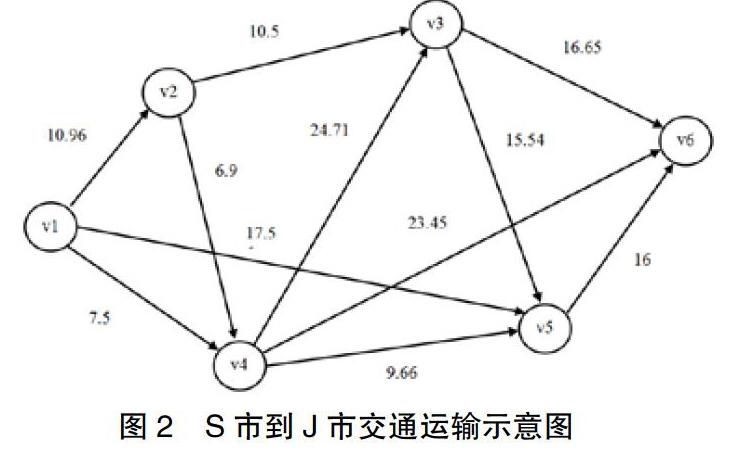
重新计算路径权值得到如下图2路径权值图：

根据权值图可以得出权值矩阵如下：

W=[0 10.96 inf 7.5 17.5 inf

inf 0 10.5 6.9 inf inf

inf inf 0 inf 15.54 16.65

inf inf 24.71 0 9.66 23.45

inf inf inf inf 0 16

inf inf inf inf inf 0]；

通过matlab仿真分析，在考虑道路快速通过的能力的情况下，从起点v1（S市） 到v6（J市） 的最短路径经过点V4 ， 路径总长度（权值）为30.95 。

3 总结

经过MATLAB程序的计算可以得出，在路程上最短的路径不一定是最优的路径，事发时的道路等级、路面质量、交通流量、车辆限制、气象条件、实时路况等条件对救援效率有着关键影响，考虑道路快速通过的能力可能得出不同的路径，因此我们在突发事件的应急救援中要综合考虑各方面因素，得出最优路径，不能只追求距离上的最短，有利于我们更好的进行救援。

由于时间的原因，本文主要探讨的是单源最短路径问题，在实际救援中，不可能仅仅是两点之间的救援，多源点单目标点的模型更加适合实际情况，在多源点的情况下，计算出来的最短路径可能有交叉路径。此时，不论从时间冲突上还是道路通行量上面都需要仔细平衡，如果不同源点的救援车辆都按照其最短路径向受灾点前进的话，很有可能造成道路交通拥挤等问题。在表示道路快速通过能力的系数计算方法上，需要根据考虑道路等级、路面质量、交通流量、车辆限制、气象条件、实时路况等条件设计出一种较为合适的计算方法[4-5]。

参考文献 ：

[1]乐阳，龚健雅.Dijkstra 最短路径算法的一种高效率实现[J].武汉测绘科技大学学报，1999，24（03）：219-222.

[2]黄纬.基于平面图的改进Dijkstra算法研究[J].江苏大学学报（自然科学版），2003，24（06）：70-72.

[3]吴必军，李利新，雷小平.基于城市道路数据库的最短路径搜索[J].西南交通大学学报，2003，38（01）：80-83.

[4]赵惠良等.城市交通非常规突发事件的应急资源调度最优路径研究[J].北京理工大学学报，2010，12（06）.

[5]刘茂.应急资源优化管理研究的主要问题[J].中国应急管理， 2007.

基金项目：2015沈阳航空航天大学生创新创业训练计划项目 项目编号：DX504308