求解最大分散度问题的混合分布估计算法

李 涛，林 耿

(闽江学院 数学系，福建 福州 350108)



求解最大分散度问题的混合分布估计算法

李 涛，林 耿

(闽江学院 数学系，福建 福州 350108)

最大分散度问题是一个NP困难问题,提出了一个有效求解最大分散度问题的混合分布估计算法.该算法利用搜索过程中的全局和局部信息来构造新解，提高了搜索的多样性，避免早熟.根据最大分散度问题的特点，构造局部搜索算法来改进分布估计算法的局部搜索能力，采用18个标准测试例子测试本研究提出的算法,与其他算法比较的结果证明了本算法是有效的.

最大分散度问题; 进化算法; 分布估计算法; 启发式算法

给定一个集合N={e1,…,en}，其中的两个元素ei和ej之间的距离为dij(dij=dji).如i≠j，则dij>0；否则，dij=0.最大分散度问题(Maximum Diversity Problem,MDP)是寻找集合N的一个具有m个元素的子集，使该子集中元素间的距离总和最大.引入n维0-1解向量x=(x1,…,xn)，xi=1表示ei被选中，否则ei没有被选中.最大分散度问题可以描述为如下的0-1规划问题：

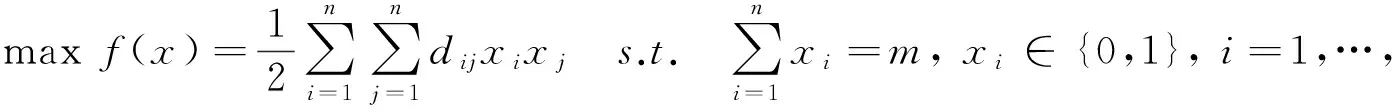
最大分散度问题是一个典型的NP困难问题，在定位、生态系统、遗传学、制造设计、课程设计等方面有着广泛的应用背景.由于精确算法只能求解较小规模的实例，近年来，元启发式算法成为人们的研究热点之一，如禁忌搜索[1-2]、贪心随机自适应搜索[3]、memetic算法[4]、变邻域搜索[5]被应用于求解大规模最大分散度问题，取得了较好的结果.

分布估计算法(Estimation of Distribution Algorithms,EDA)是一种基于统计原理的随机优化算法，它已经成功应用于求解许多组合优化问题[6-8].然而，由于EDA过多侧重于解空间宏观的全局优化，单纯的EDA局部搜索能力有限，算法后期易陷入早熟收敛.

本研究根据最大分散度问题的特点，提出了一个混合分布估计算法(HEDA).该算法利用搜索到的解的局部信息和分布估计算法的全局信息来产生新的解向量，采用基于迭代改进的局部搜索算法来改进局部搜索能力.用一些国际标准测试例子测试本算法并与现存算法比较，证明了本算法的有效性.

1 混合分布估计算法的主要组成模块

求解最大分散度问题的HEDA是一种将统计学习方法与进化算法有机结合的种群算法，它主要包含3个基本子模块：①概率模型；②新解的产生方法；③局部搜索算法.算法的基本步骤如下：首先，构造多样性较好的初始种群，通过对优势解集建立概率模型获得候选解的分布特征，通过新解的产生方法构造新的解向量.然后，采用局部搜索算法对新解进行再优化，用再优化后得到的解对种群进行更新.接下来，混合分布估计算法重复以上步骤，直到满足算法的停止准则.

下面对求解最大分散度问题的HEDA的3个子模块——概率模型、新解的产生方法和局部搜索算法分别进行详细介绍.

1.1 概率模型

HEDA采用n维概率向量p=(p1,…,pn)来描述解空间分布的概率模型，其中pi表示第i个元素ei被选中的概率，即xi=1的概率.

HEDA是一种种群进化算法.从一个初始的概率向量开始，分布估计算法的每一代都通过种群中的优势解集来更新概率向量.假设当前的种群包含s个解，记为S=(x1,…,xs).首先，HEDA从种群S中找出最好的t个解，记为{y1,…,yt}.然后，HEDA通过式(1)来更新概率向量：

(1)

式中：0≤λ≤1表示学习速率.

对于大部分组合优化问题来说，它们的优势解具有相似的结构.利用式(1)来更新容易导致算法过早收敛.为了产生多样性的解、避免早熟，HEDA对概率模型进行了如下修正：

(2)

1.2 新解的产生方法

遗传算法通过交叉和变异来构造下一代解向量.交叉和变异操作都是随机进行的，可能无法继承精英解的优良结构.另外，由于没有利用搜索到的全局信息，所以导致遗传算法在一定程度上出现了退化.

分布估计算法有效利用了解空间的分布情况，通过概率模型来产生新的解向量.但是，分布估计算法没有利用到搜索的局部信息，导致算法的局部搜索能力不足.

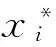
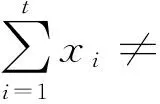
新解产生的具体步骤如下：

输入相关参数.

输出新解x.

第1步 初始化i=1.

第2步 产生一个随机数δ∈[0,1].

第4步 产生一个随机数κ∈[0,1].如果κ≤pi，令xi=1；否则，令xi=0.

第5步 令i=i+1.如果i≤n，转第2步；否则，转第6步.

第8步 停机，输出新产生的可行解x.

1.3 局部搜索算法

局部搜索算法是进化算法求解过程中消耗时间最多的模块.提高局部搜索算法的复杂度能够有效减少整个算法的求解时间，故设计高效的局部搜索算法是一个非常重要的环节.

HEDA通过局部搜索算法来有效提高算法的局部搜索能力.Kernighan和Lin[9]提出了一个求解划分问题的高效局部搜索算法——KL算法.KL算法已经被成功地应用于求解许多NP困难问题，HEDA改进KL算法为局部搜索算法，该局部搜索算法在提高解的质量的同时还可保持解的可行性.

给定一个解x=(x1,…,xn)，设Z(x)={i|xi=1}表示选中的元素的集合，U(x)={i|xi=0}表示未选中的元素的集合.Z中的一个元素k与U中的一个元素j交换后，会产生一个新的可行解x′，将交换后目标函数值的改变量定义为交换k与j的增益g(k,j)，即

g(k,j)=f(x′)-f(x).

(3)

局部搜索算法是一个迭代改进算法，由一系列的pass组成.局部搜索算法从一个初始解x0开始，在每一个pass的开始阶段，所有元素都能够自由移动.设Zf和Uf分别表示选中和未选中的自由元素组成的集合.HEDA通过式(3)计算出所有自由元素交换后的增益，选择增益最大的组合进行交换，交换后的两个元素在该pass中禁止再次移动.每个pass执行以上交换σ次后停止，将该pass中找到的最好的解xb输出.如果当前pass能够找到更好的解，HEDA以xb为初始解，继续下一个pass；否则，局部搜索算法停止，将该过程中找到的最好的解输出.

局部搜索算法的具体步骤如下：

输入可行解x0.

输出改进后的解xb.

第1步 初始化x=x0，xb=x0.

第2步 令Zf=Z(x)，Uf=U(x)，初始化iter=0.

第3步 由式(3)计算出所有g(k,j)，κ∈Zf，j∈Uf.

第4步 找出κ*，j*,使g(κ*,j*)最大.令xκ*=0，xj*=1.令Zf=Zf-{κ*}，Uf=Uf-{j*}.

第5步 如果 f(x)>f(xb)，则xb=x.

第6步 令iter=iter+1.如果iter≤σ，转第3步；否则，转第7步.

第7步 如果f(xb)>f(x0)，则x0=xb，转第1步；否则，停机，输出改进后的可行解xb.

2 HEDA的算法描述

假设L为算法的最大迭代次数，下面给出了求解最大分散度问题的混合分布估计算法的具体步骤：

输入相关参数.

输出近似最优解x*.

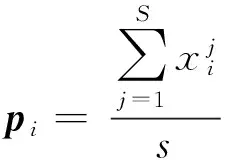
第4步 从种群S中找出t个最好的解，利用式(1)和式(2)更新概率向量.

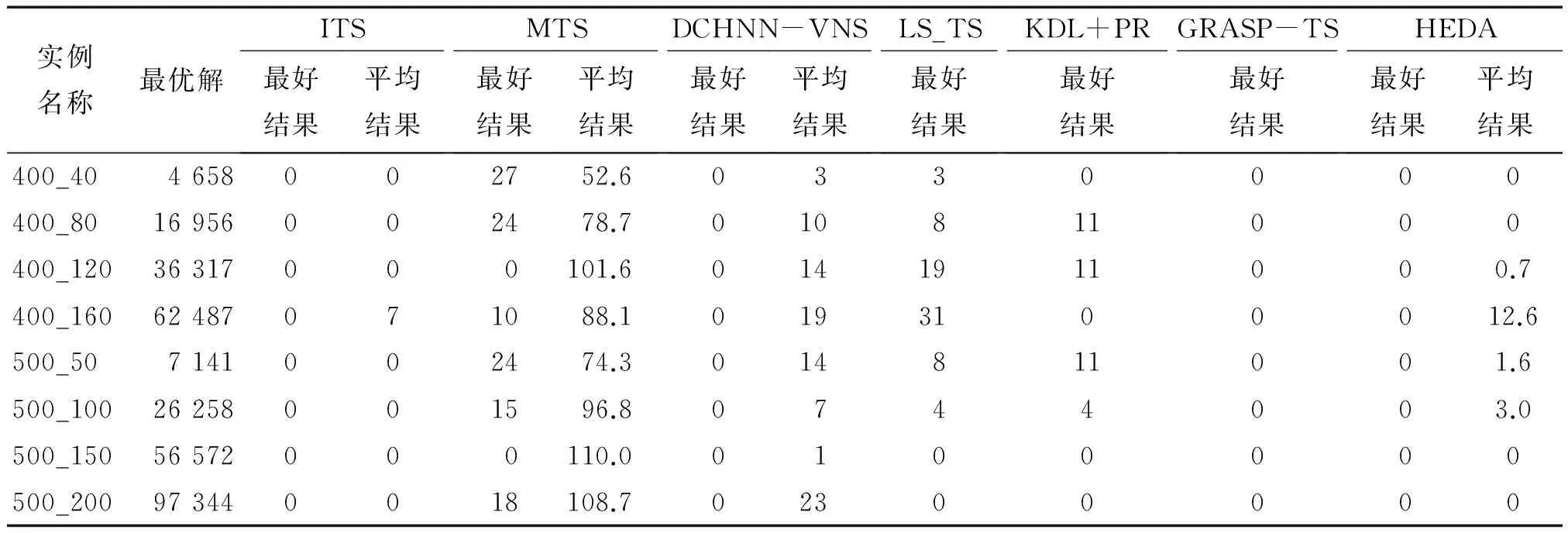
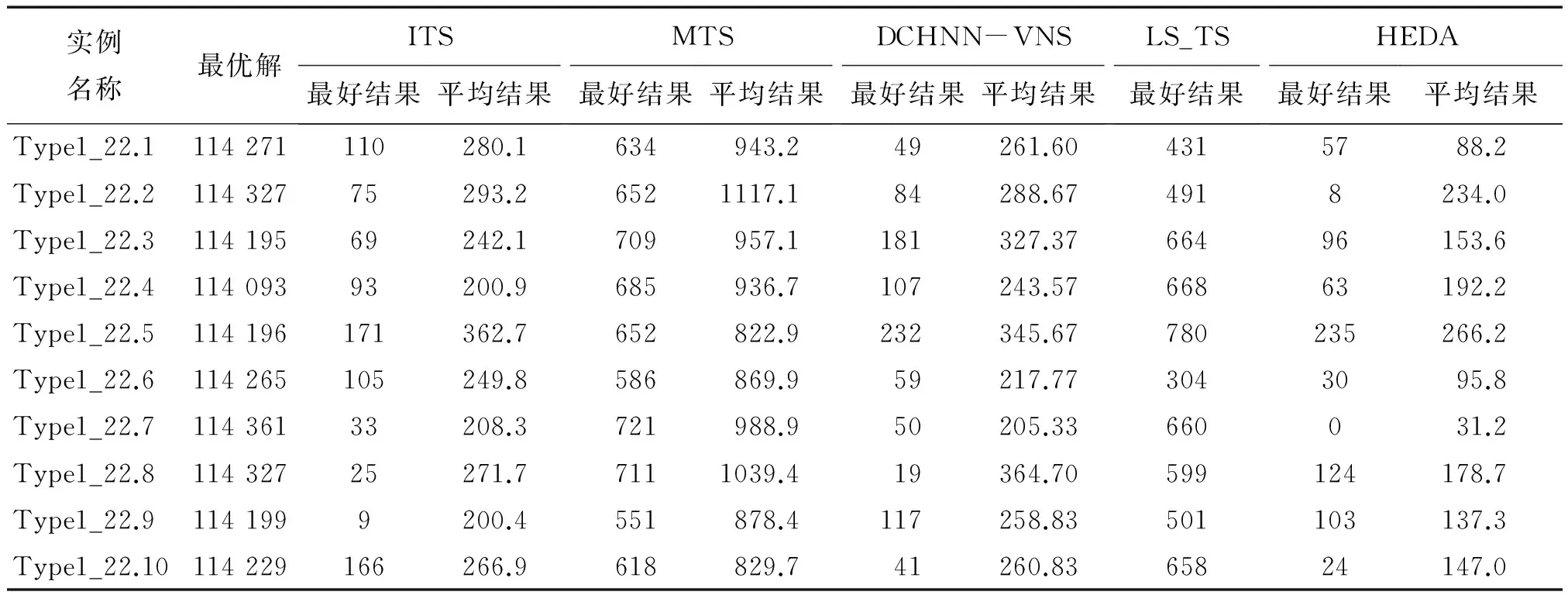
第5步 令g=g+1，如果g

3 实验

为了检验HEDA算法的性能，本研究用C语言编写算法的程序，在CPU主频为3.40 GHz的计算机上测试.根据前期试验结果，算法的参数设置如下：s=12，λ=0.7，α=0.7，σ=0.4m，L=200.

3.1 测试例子

采用2个数据集的18个国际标准测试例子来测试提出的算法，测试例子的规模为400～2 000.

(1)集合1(Silva实例)：n∈[100,500]，m∈{0.1n,0.2n,0.3n,0.4n}，dij是从区间[0,9]中随机产生的整数.由于小规模的例子比较容易求解，故本研究采取n=400和n=500的8个例子来测试.

(2)集合2(随机类型实例)：这些测试例子的集合由文献[10]提出，本研究取其中规模最大的10个例子(n=2 000，m=200，dij∈(0,10))来测试算法.

3.2 实验结果与分析

对于18个标准测试例子，分别运行HEDA 5次.表1和表2分别给出了运行集合1和集合2的每个测试例子的最好结果和平均结果.为了与迭代禁忌搜索(ITS)、Macambira的禁忌搜索(MTS)、禁忌与GRASP混合算法(LS_TS[11]和GRASP-TS[12])、路径重链算法(KLD+PR)、神经网络和变邻域算法(DCHNN-VNS)比较，表1和表2也列出了这些启发式算法的结果.

表1 HEDA与其他启发式算法求解Silva实例的实验结果比较Tab.1 Comparison results of HEDA with other heuristics on Silva instances

表2 HEDA与其他启发式算法求解随机类型实例的实验结果比较Tab.2 Comparison results of HEDA with other heuristics on random instances

从表1给出的结果可以看出，ITS,DCHNN-VNS,GRASP-TS,HEDA在8个例子上都能找到最优解，并且HEDA得到的平均结果优于MTS,DCHNN-VNS,LS_TS和KDL+PR，但是比ITS差.

从表2给出的测试结果可以看出，HEDA在10个例子上都找到了比MTS和LS_TS更好的最优解，分别在6个例子和7个例子上获得了比ITS和DCHNN-VNS更好的最优解.HEDA在10个例子上都获得了比其他算法更好的平均解.

以上结果表明，从算法的求解结果来看，本研究提出的算法优于MTS,DCHNN-VNS,LS_TS和KDL+PR，并且比其他算法稳健.HEDA能够有效地避免早熟，是求解最大分散度问题的有效算法.

4 结束语

本研究构造了求解最大分散度问题的混合分布估计算法.该算法从一个随机的初始种群开始，利用概率模型收集全局信息，与当前最优解的局部信息相结合来构造新解.然后，根据最大分散度问题的特点，构造局部搜索算法来提高局部搜索能力.最后，通过种群更新方法来保持种群的多样性.这些策略有效地组成了一个有机的整体，提高了搜索的效率.与现存的一些算法比较，本研究提出的混合分布估计算法是一种求解最大分散度问题的有效算法.然而，局部搜索的算法复杂度比较高，求解速度较慢，课题将进一步研究更加有效的局部搜索算法来提高算法的效率.

[1] PALUBECKIS G.Iterated tabu search for the maximum diversity problem[J].Applied Mathematics and Computation,2007,189(1):371-383.

[2] WANG Y,HAO J K,GLOVER F,et al.A tabu search based memetic algorithm for the maximum diversity problem[J].Engineering Applications of Artificial Intelligence,2014(27):103-114.

[3] SILVA G C,ANDRADE M,OCHI L S,et al.New heuristics for the maximum diversity problem[J].Journal of Heuristics,2007,13(4):315-336.

[4] DEFREITAS A R R,GUIMARAES F G,SILVA R C P,et al.Memetic self-adaptive evolution strategies applied to the maximum diversity problem[J].Optimization Letters,2014,8(2):705-714.

[5] 周雅兰，王甲海，闭玮，等.结合变邻域搜索的竞争Hopfield神经网络解决最大分散度问题[J].计算机科学,2010,37(3):208-211.

[6] 王勇臻，陈燕，李桃迎，等.元胞分布估计算法求解高维0/1背包问题[J].小型微型计算机系统，2015，36(6):1341-1346.

[7] 余娟，冯晓华，贺昱曜.求解多维背包问题的改进分布估计算法[J].计算机仿真，2014,31(10):286-290.

[8] HAUSCHILD M,PELIKAN M.An introduction and survey of estimation of distribution algorithms[J].Swarm and Evolutionary Computation,2011(3):111-128.

[9] KERNIGHAN B W,LIN S.An efficient heuristic procedure for partitioning graphs[J].Bell System Technical Journal,1970,49(2):291-307.

[10]MACAMBIRA E M.An application of tabu search heuristic for the maximum edge-weighted subgraph problem[J].Annals of Operations Research,2002(117):175-190.

[11]DUARTE A,MARTI R.Tabu search and GRASP for the maximum diversity problem[J].European Journal of Operational Research,2007,178(1):71-84.

[12]ARINGHIERI R,CORDONE R,MELZANI Y.Tabu search versus GRASP for the maximum diversity problem[J].40R,2008,6(1):45-60.

A hybrid estimation of distribution algorithm for solving the maximum diversity problem

LI Tao，LIN Geng

(DepartmentofMathematics,MinjiangUniversity,Fuzhou350108,China)

The maximum diversity problem is known to be NP-hard. In this paper,an efficient hybrid estimation of distribution algorithm is proposed to solve the maximum diversity problem. The proposed algorithm uses the local information and the global information to generate new solutions. It diversifies the search and prevents the premature convergence. According to the structure of the maximum diversity problem,a local search procedure is developed to enhance the exploitation of estimation of distribution algorithm. The experiments were done on 18 benchmark instances from the literature. Numerical results and comparisons with other existing algorithms indicate that the proposed algorithm is efficient.

maximum diversity problem; evolutionary algorithm; estimation of distribution algorithm; heuristic

2016-07-06

福建省自然科学基金项目(2016J01025);福建省高校新世纪优秀人才支持计划;大学生创新创业训练项目(201510395049)

李涛(1994-)，男，广东汕头人，本科生，研究方向为应用数学与人工智能.

林耿(1981-)，男，福建莆田人，副教授，博士，研究方向为组合优化与人工智能.E-mail:lingeng413@163.com.

O221.4

A

1674-330X(2016)04-0069-05