基于贝叶斯和Bootstrap方法的传感器网络节点可靠性评估

何永强，董金超，朱子牮

(1.河南工程学院 计算机学院，河南 郑州 451191；2.河南工程学院 理学院，河南 郑州 451191；3.中原工学院 软件学院，河南 郑州 450007)



基于贝叶斯和Bootstrap方法的传感器网络节点可靠性评估

何永强1，董金超2，朱子牮3

(1.河南工程学院 计算机学院，河南 郑州 451191；2.河南工程学院 理学院，河南 郑州 451191；
3.中原工学院 软件学院，河南 郑州 450007)

针对传感器节点故障样本数据较少和传统可靠性评估方法无法有效进行评估的问题，提出了基于贝叶斯理论在小样本数据下采用Bootstrap方法依据原生样本平均无故障间隔时间进行多次抽样生成再生样本的分布，选取Weibull分布为验前分布，推导确定可靠性的验后分布.通过仿真分析，验证了小样本数据下传感器节点可靠性评估结果的准确性，为小样本数据下的可靠性评估提供了新的思路和方法.

贝叶斯；Bootstrap；传感器节点；可靠性评估；小样本数据；Weibull分布

传感器网络是由部署在检测区域内具有计算和通信能力的微小传感器节点组成的，可通过自组织方式采用多跳的方式进行通信，能根据环境自主完成指定任务的分布式智能化网络系统[1-2].一般情况下，传感器网络故障是由传感器节点故障引起的，由于节点廉价、自身能量有限、所处环境等因素的影响，节点采集到的数据可能有误,甚至节点失效[3-5].随着设计和制造水平的不断提高，航空航天、军工、大型复杂网络等领域对数据采集的要求比较严格，对电子产品可靠性的要求也越来越高.可靠性评估是传感器节点研究开发过程中的重要部分，由于受到研发成本、试验条件、试验周期等条件的制约，节点设备往往投试非常小的数量，很难进行大量试验，在试验过程中常采用小样本定时截尾方案[6].因此，研究传感器节点的可靠性评估,特别是在小样本情况下的可靠性评估有着重要的现实意义.

马智博等[7]提出了正态总体的小样本数据下概率密度拟合分布的结论，但采样数据必须满足正态分布的取样数据，否则将影响概率密度分布；朱德馨等[8]提出了基于Bayes方法和最小二乘法进行极小样本下高速列车轴承的可靠性评估方法，但如果试验数据失效、先验分布确定不好，将会导致评估效果很差；Ross和Jacquelin[9-10]提出了极大似然的修偏方法，但如果随机小样本无法满足某种分布，将会影响参数估计的正确性；丛伟等[11]提出了矩估计的修偏法，即中值无偏矩估计法，但如果样本数据不够大，将直接影响总体参数估计值；高攀东等[12]提出了一种基于Weibull分布和小样本数据的可靠性评估新方法，但采用的数据样本如果不符合Weibull分布，将无法对小样本数据进行可靠性评估.在总结已有研究成果的基础上，本课题采用Bootstrap方法对经验样本数据进行Bootstrap抽样，得到了传感器节点平均无故障间隔时间的离散分布，并将Weibull分布作为传感器节点平均无故障间隔时间的先验分布，对节点的可靠性进行贝叶斯验后推断，得到了传感器节点的可靠性评估模型.

1 贝叶斯评估方法

贝叶斯评估方法首先假设随机变量X有一个给定参数θ的密度函数p(x|θ)，在θ∈Θ的条件下随机抽取样本X1，X2，…，Xn都含有Θ的有关信息；描述随机变量θ的先验分布从先验信息中归纳出来，其密度函数为π(θ)，则随机变量θ的后验分布[13-14]为

(1)

因此，在贝叶斯方法中，先验信息的采集、获取、融合等问题是信息处理的关键，选取合理的先验分布是样本可靠性评估的关键.

1.1 先验信息的处理

运用贝叶斯评估方法时，采用Efron[15]提出的Bootstrap方法来选取先验分布中的参数值，优点是可以通过计算机对现有的样本数据进行再抽样处理产生新的样本数据，通过样本数据模拟总体分布.本研究选用非参数再抽样样本的方法进行数据的抽样处理，得到再生新样本[16-17]，具体过程如下：

(1)在区间[0,1]上产生均匀分布的随机数λ；

(2)设xi为现有原始样本数据x=(x1,x2,…,xn)从小到大排序后的第i个数据；

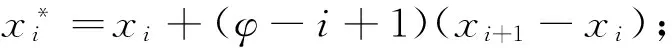
1.2 验后分布处理

Weibull分布是可靠性分析和寿命检验的理论基础，应用较为广泛，如电子产品和设备的可靠性评估.Weibull分布的概率密度函数即先验分布为

(2)

式中:x是随机变量且x≥0，λ是比例参数且λ>0，m是形状参数且m>0.

用Weibull分布的期望值作为服从Weibull分布的可靠性均值,即

(3)

根据先验信息处理可以得出可靠性的先验分布为

(4)

对于试验信息X中的数据x1，x2，…，xr，xr+1，…，xn(r为失效序号)进行截尾处理，则截尾试验样本的似然函数

(5)

根据比例参数λ和形状参数m的先验联合概率密度函数π(m,λ)，由贝叶斯公式可以得到验后联合概率密度

(6)

则由式(4)至式(6)得出可靠性的验后分布

(7)

2 仿真与分析

2.1 方法有效性验证

根据以上算法，选取某型号的传感器节点的故障信息，采集到的节点故障间隔时间为424.3 h，479.5 h，2 133.1 h，1 482.3 h，2 332.1 h，2 415.5 h，2 647.8 h，2 822.1 h，3 121.2 h，3 644.9 h，3 761.2 h，3 898.3 h，4 072.1 h，4 301.2 h，5 409.1 h，5 601.3 h，5 708.2 h，6 019.2 h，6 918.9 h，9 561.2 h，9 955.2 h，11 263.1 h，11 388.9 h，13 182.1 h，13 471.2 h，4 801.3 h，5 802.1 h，15 795.2 h，16 719.1 h，17 543.0 h，19 401.5 h.

将以上取得的原生样本从小到大排序，然后进行10 000次自助样本的抽取，用最小二乘法得到Weibull分布参数值，得出平均无故障间隔时间的频率密度分布，如图1所示.

选取Weibull分布作为平均无故障间隔时间参数的验前分布，根据图1进行拟合，得出先验分布的比例参数λ=6 804.2、形状参数m=12.18.采用D检验法[18-19]得出观测值为0.109，临界值为0.214.因观测值小于临界值，说明验前分布的稳健性较好，即验前分布可以选用Weibull分布.

根据设计要求，节点平均无故障时间要达到10 000 h以上，故选择10个节点设备进行截尾试验，截尾时间设定为40 000 h，测试结果如表1所示.

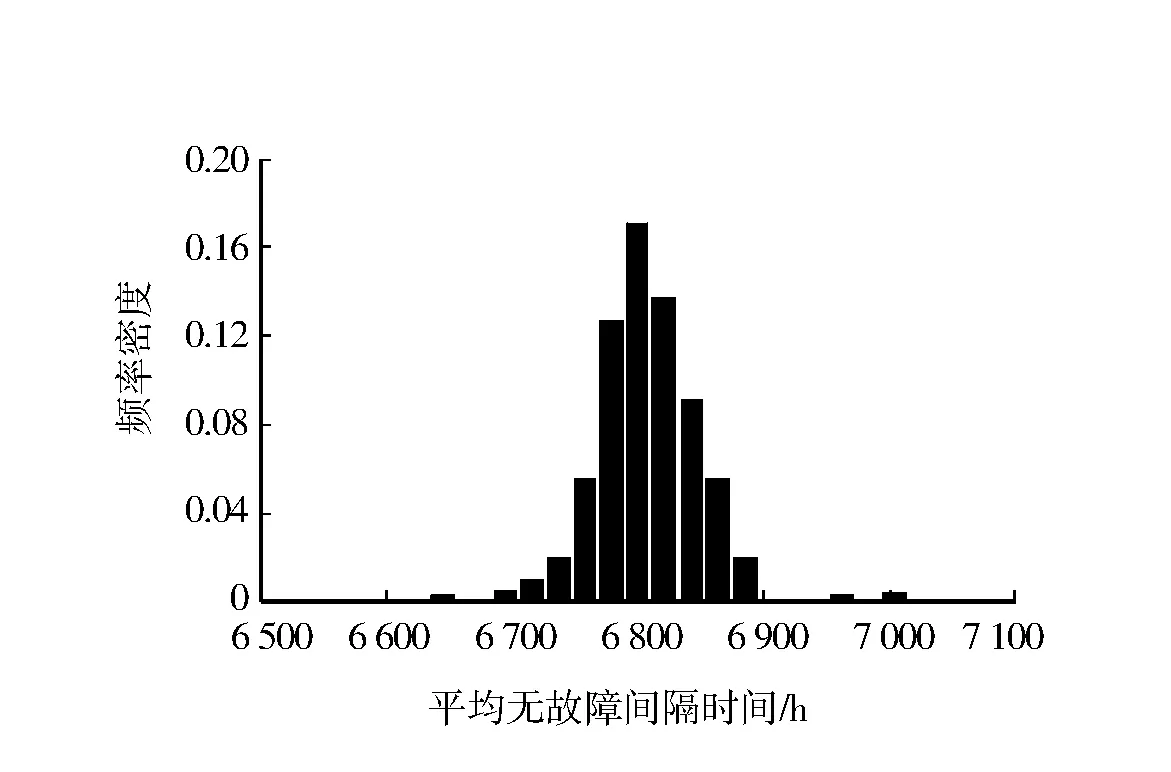
图1 平均无故障间隔时间的频率密度分布直方图Fig.1 Frequency density distribution histogram of mean time between failure

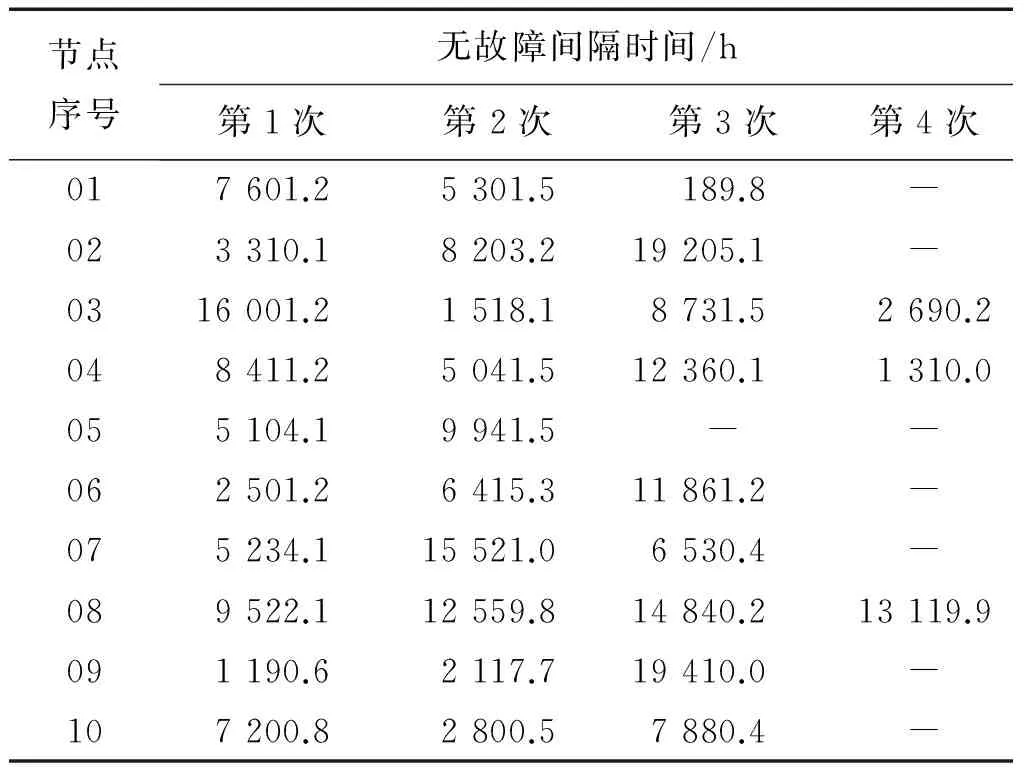
表1 截尾试验得到的平均无故障时间间隔Tab.1 Mean time between failure after censoring test

根据比例参数λ=6 804.2、形状参数m=12.18，由式(7)可得平均无故障间隔时间为10 112.5 h，评估结果达到了预定目标，这说明基于贝叶斯理论的小样本可靠性评估结果比较准确.

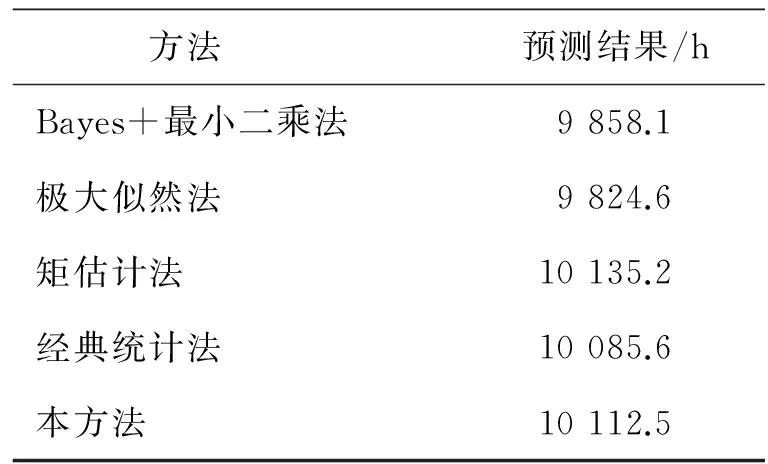
表2 预测结果对比Tab.2 Predictions comparison

2.2 对比分析

为了验证本研究提出方法的可靠性、预测精度及优势，采用不同方法对平均无故障间隔时间进行了预测评估，与经典统计法、Bayes+最小二乘法、极大似然法、矩估计法进行对比，结果如表2所示.经典统计法的预测准确度比本方法高，但它只考虑试验采集到的数据，如样本中有失效数据，将无法使用该方法进行预测评估.因此，在小样本情况下，本方法的预测准确度更高、可靠性与适用性更好.

3 结语

基于贝叶斯理论对传感器网络的可靠性进行评估，结合Bootstrap方法依据原生样本数据进行试验再生成样本数据来扩大样本量，选取Weibull分布作为验前分布并进行了稳健性仿真试验，验证了平均无故障间隔时间的可靠性评估结果与该方法的优越性.在小样本数据的情况下，不作任何主观假设，贝叶斯理论和Bootstrap方法大大弥补了小样本数据信息量的不足，对小样本数据的可靠性评估具有一定的借鉴意义.

[1] 崔逊学,左从菊.无线传感器网络简明教程[M].北京：清华大学出版社，2009.

[2] 何永强,张文欣,李可.基于贝叶斯理论的传感器网络节点故障检测方法[J].河南工程学院学报(自然科学版)，2014，26(4):65-68.

[3] ABOELAZE M,ALOUL F.Current and future trends in sensor networks：a survey[J].Wireless and Optical Communications Networks,2005,68(3):551-555.

[4] KOUSHANFAR F,POTKONJAK M,SANGIOVANNI V.A fault tolerance techniques for wireless and hoc sensor networks[J].Proceedings of IEEE on Sensors,2002(2):1491-1496.

[5] 何永强,宫玉荣,朱予聪.基于贝叶斯和层次模型的传感器网络节点故障预测研究[J].河南工程学院学报(自然科学版)，2015，27(4):63-68.

[6] SIRVANCI M,YANG G.Estimation of the Weibull parameters under type I censoring[J].Journal of the American Statistical Association,1984,79(385):183-187.

[7] 马智博，朱建士，徐迺新.有关正态分布的小样本可靠性评估[J].核科学与工程，2003,23(4)：332-336.

[8] 朱德馨，刘宏昭.极小样本下高速列车轴承的可靠性评估[J].中南大学学报(自然科学版)，2013，44(3):963-969.

[9] ROSS R.Bias and standard deviation due to Weibull parameter estimation for small data sets[J].IEEE Transactions on Dielectrics and Electrical Insulation,1996,3(1):28-42.

[10]JACQUELIN J.Generalization of the method of maximum likelihood[J].IEEE Transactions on Electrical Insulation,1993,28(1):65-72.

[11]丛伟，陈晓阳，王志坚,等.Weibull分布产品小样本定时截尾试验方案下的可靠性评估[J].中国机械工程，2013,24(14)：1891-1896.

[12]高攀东，沈雪瑾，陈晓阳，等.基于自助法的小样本Weibull分布可靠性分析[J].机械设计与研究，2015,31(2): 164-167.

[13]蔡洪，张士峰，张金槐．Bayes试验分析与评估[M].长沙：国防科技大学出版社，2004.

[14]盛骤，谢式千，潘承毅.概率论与数理统计[M].4版.北京：高等教育出版社，2011.

[15]EFRON B．Bootstrap methods：auother look at the jacknife[J].Ann Statist，1979(7)：1-26．

[16]戴邵武，高华明，肖支才.基于自助法的小样本数据分析方法研究[J].海军航空工程学院学报，2009,24(1):27-30.

[17]黄玮，冯蕴雯，吕震宇.基于Bootstrap方法的小子样试验评估方法研究[J].机械科学与技术，2006,25(1):31-35.

[18]华中师范大学，中国标准研究中心，北京大学.GB/T 4882—2001数据的统计处理和解释正态性检验[S].北京:中国标准出版社,2001.

[19]俞钟行.D检验法[J].地质与勘探，1990(2):45-46.

Research of sensor networks nodes reliability evaluati on based on Bayesian and Bootstrap methods

HE Yongqiang1,DONG Jinchao2，ZHU Zijian3

(1.CollegeofComputers，HenanUniversityofEngineering，Zhengzhou451191，China;2.CollegeofSciences，HenanUniversityofEngineering，Zhengzhou451191，China;3.SoftwareCollege,ZhongyuanUniversityofTechnology，Zhengzhou450007，China)

In order to solve the problem of little fault date of sensor networks nodes,and that traditional reliability evaluation method cannot be used to assess. A method on Bayesian of sensor networks nodes was proposed under the conditions of small sample. Distribution of regeneration sample is obtained based on mean time between failure of native sample by conducting Bootstrap sampling repeatedly. Weibull distribution is chosen as the prior distribution,calculation model were deduced to obtain reliability posteriori distribution. Through simulation analysis,the accuracy of sensor nodes reliability evaluation results under small sample data is verified,providing news ideas and methods for reliability evaluation results under small sample data.

Bayesian; Bootstrap; sensor nodes; reliability evaluation; small sample data; Weibull distribution

2016-04-19

河南省科技计划课题(152102210027)；河南省高等学校重点科研项目(15A520054)

何永强(1977-)，男，河南扶沟人，副教授，研究方向为计算机应用、信息管理与信息系统.

TP393.07

A

1674-330X(2016)04-0053-04