SAT问题子句消去法快速求解

姜咏江，陈跃

（1. 对外经济贸易大学离退休处，北京朝阳，100013；2. 西安交通大学，陕西西安，710000）

SAT问题子句消去法快速求解

姜咏江1，陈跃2

（1. 对外经济贸易大学离退休处，北京朝阳，100013；2. 西安交通大学，陕西西安，710000）

布尔可满足性问题（SAT）是最基本的NPC问题，直接涉及到集成电路设计优化、生物基因、人工智能、互联网等诸多领域的快速计算。给出了一种子句消去法，运用限位数、子句块和关联段等概念，探索出了用确定法则快速求出SAT满足解的计算方法，为纯离散变量计算找到了一种新途径。

SAT问题；限位数；子句消去法；子句块；关联段；多项式时间复杂度

引言

P/NP问题是世界难题。这个问题最早要追溯到上个世纪50年代[1]，是由数学家库尔特·哥德尔向计算机发明人之一冯·诺依曼提出的。1971年，斯提芬·库克给出了NP类问题的定义[2]，并指出：只要NP-complete一类问题其中之一存在多项式时间复杂度算法，就可以认定NP=P。斯提芬·库克的观点已被学术界广泛接受[3]。

SAT问题被认为是NP-complete一类问题中最基本的问题[4]，直接涉及到集成电路设计优化、生物基因、人工智能、互联网等诸多领域的快速计算，但以往没有学者找到SAT的多项式时间复杂度的快速算法。本文给出的子句消去法能够快速准确地求出SAT满足解。

1 SAT问题与限位数

SAT问题可以用数码0和1来表示，这与限位数理论关系密切。

1.1 SAT问题定义

“逻辑变量和变量非形式组成的多项式若干个，求它们与运算结果为真的解问题”就是SAT问题，每个逻辑多项式叫子句。严格定义如下：

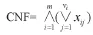
1.2 SAT问题的0和1表示

合取范式CNF可用数码“0”表示xij'，用“1”表示xij。那么，式（1）的CNF就可通过表1的形式来表达。

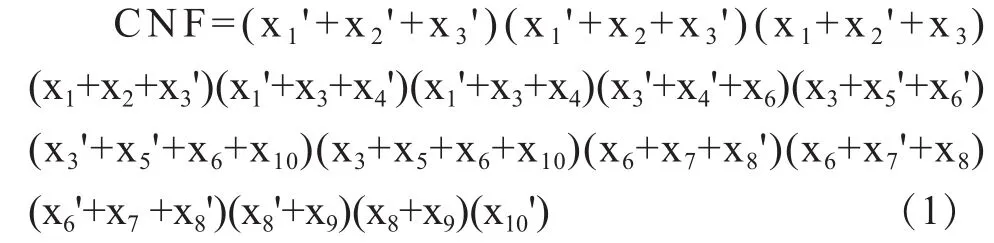
表 1 CNF的0和1表示

表1的表头是逻辑变量，每一行是一个子句。子句与子句之间是逻辑与运算的关系，子句的列与列之间是逻辑或的关系。每列的0和1为表头逻辑变量的表现值。

从表1可以看到，只要将逻辑变量设定为0（或1），那么这个变量所在的一列表现值为0（或1）的子句的逻辑值一定是1。那么就可以将这些值为1的子句消去，剩下的部分不会影响到CNF=1的继续求解。将CNF的所有变量均如此设定后，如果没有子句剩下，那么就可以断定设定的变量值全体即是CNF=1的一个满足解。可惜的是，这种设定方法具有随机性，并不能一次性确定出CNF=1的解。这需要一套准确无误设定变量值的方法，才能保证其不具有随机性。为此，需要找出CNF的特有结构关系。

定义2 变量相同的子句组成子句块，这些变量所有可能子句组成的子句块称作完全块。

1.3 限位数与子句块

位数一定的数称作限位数。限位数的无效0不能省略[5]。易知k位二进制数共有2k个。显然，k个变量组成的完全块共有2k个子句，超过这个数就会出现子句重复。

表2是3位二进制完全块，共有8个子句。

表2 3位完全块

定理1 完全块CNF=1无解。

证明：不失一般性，从表2容易看出，k位完全块每一个变量的0和1表现值都有2k-1个。这一特征表明，无论如何设定完全块逻辑变量的值，都不可能使所有的子句值为1，即总有值为0的子句。证毕。

进一步分析完全块，可见每一个子句都有一个反码数，这样的两个子句就称作互反子句。容易知道，不是互反子句至少有一位数码相同。因此，子句块中不存在反子句的子句表现值一定能将这个子句块的全部子句消去。还可见，如果非完全块有一个变量有2k-1个0或1，这个变量不设定这个表现值，那么就剩下了k-1个变量的完全块，就会造成无法设定变量值使得CNF=1。

定义3 变量只有一个值不使CNF=1无解，这个值称作变量唯一解。

定理2 非完全块的变量有2k-1个0（或1）表现值是变量唯一解。

证明：不失一般性，从表2容易看出，k位非完全块变量有2k-1个0（或1）表现值。若设定0（或1）为这个变量值，那么这个变量的表现值为1（或0）的子句，不考虑这个变量不构成完全块，反之，为0（或1）子句就构成完全块。因此，变量的2k-1个0（或1）表现值是变量唯一解。证毕。

定义4 子句块通过相同变量关联组成关联段。

定义5 设定变量值，依据定理2消去子句，若关联段剩余子句块没有变量矛盾值，则称设定值为这个变量的可选解。

表3是依据定理2，对表1设定x9=1，x10=0消去相关子句后，得到的剩余部分（浅灰色列已设定）。这部分均没有子句块的变量唯一解，于是需要测试变量的可选解。

令x1=1，考虑消去子句（横向纹理所示）后，出现x3在子句块x2x3中有唯一解0，而在子句块x3x4中有唯一解1，如此一来，无论如何都不可能确定x3的值使CNF=1。说明x1没有可选解1。

表3 x1=1不是可选解

再对x1测试可选解0，没有出现变量值矛盾的情况。说明0是变量x1的唯一解。设定x1=0，消去相关的子句，就得到了可以继续求解的表4。

表4 设定变量唯一解消去子句

2 子句消去法求解与验证

有了变量唯一解和变量可选解的概念，就可以通过先设定它们的值，求出CNF=1的满足解。

2.1 基本规则

用子句消去法求CNF=1的满足解要用到两条规则。

规则1：子句块变量有唯一解必须首先设定。

依据定理2，表1中的子句块x10和子句块x8x9有唯一解x10=0和x9=1，消去值为1的那些子句，就得到表3（不包括左上角的x1=1）。

规则2：变量有唯一可选解必须优先设定。

通过表3对x1=1的检测可知，1不是这个变量的可选解。同理检测可知x1=0是可选解。则设定x1=0，消去相关子句，得到表4后还可继续求解。

2.2 快速判定可选解

表4中剩下的子句块中没有变量唯一解，需要像测试x1一样，检查这些变量是否有唯一可选解。这个过程实际上无需检测所有变量。

引理1 若非完全块中没有变量唯一解，则至少没有一对互反子句。

证明：在k个变量的非完全块中，没有变量唯一解也即无任一变量有2k-1个相同表现值，从完全块可知，这至少要有一对互反子句不存在方可。

引理2 不在子句块中互反子句的任意一个作为块变量值，都可使子句块的全部子句值为1。

证明：因为子句块中的子句都不是这对互反子句的反子句，那么至少有一个位置的数码与它们相同。因而用这对互反子句的任意一个作为子句块变量设定值，都可使子句块的全部子句值为1。

引理3 CNF=1有解，这个解也是子集的解。

证明：显然，CNF=1的解使每个子句值为1，因而这个CNF的子集子句的值也都是1。

定义6 检测变量可选解所涉及的关联段称为变量关联段。

定理3 没有变量唯一解的非完全块，非关联变量都有2个可选解。

证明：根据引理1，没有变量唯一解的非完全块，一定有互反子句能够消去这个子句块的全部子句。那么，非关联变量不论设定0或1值，都只消去本子句块的子句，与其它子句块无关，因而不会出现剩余完全块，知此定理成立。

定理3减少了要判断可选解变量的数量，提高了计算速度。

定理4 每个变量都有2个可选解的CNF，任选一个变量设定值，消去剩余子句块变量唯一解子句，最终可得CNF=1的解。

证明：根据变量关联段的定义，设定一个变量可选解，消去一些子句，未被消去变量的关联段剩下了原变量关联段的子集，依据引理3，这并不影响剩余变量的可选解数量。因而可再如此设定剩余变量的值，消去相关子句，最终可得CNF=1的满足解。

2.3 子句消去法解题

根据规则1和规则2，以及定理4，很容易计算出SAT的满足解。作为例子，继续计算最初表1给出的CNF=1的满足解。

通过检验知，关联变量x3和x6都有2个可选解。则依据定理3知，所有的剩余变量都有2个可选解。为此任意设定x3=0，得到x2唯一解0，消去相关子句后得到表5。

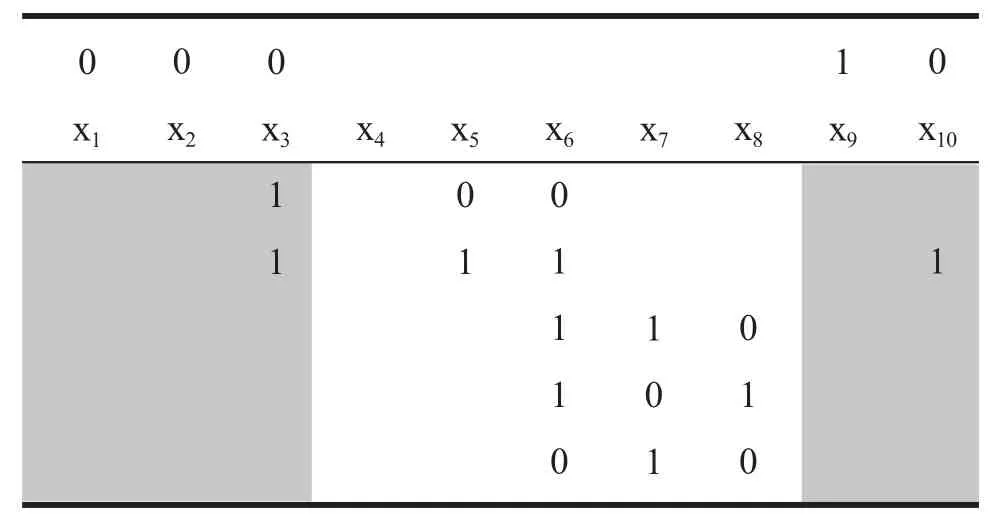
表5 x3=0，x2=0消去相关子句

表5剩下的变量仍然都有2个可选解，继续设定x6=1，消去子句。进而得到x5=0这个变量唯一解。消去相关子句，得到表6。

表6 x6=1，x5=0消去相关子句

最终可设定x7=1，或者x8=0消去相关子句，得到最后的满足解如表7上方一行所示，*号表示该变量取值0或1均可。

2.4 CNF=1满足解验证

对于子句消去法计算得到的全体变量值是否是CNF=1的解，是可以验证的。一种办法是将每个变量求出的值（*可以任意取值0或1），代入CNF的逻辑表达式，检验最终结果是否是CNF=1。

表7 CNF=1的解验证

不妨介绍一个简单的验证方法，即将所求解值置入原题（表1）的上面，检验每一行是否有与其变量值相同的子句表现值。若有，则将子句消去，若最终没有子句剩下，就说明得到的解完全正确。

本题如果x7不选，令x8=0，也可将全部子句消去，从而完成解的验证。

3 结论

本文介绍的子句消去法可以保证快速计算出SAT问题的一组满足解，而不是全部解。当然全解也可用子句消去法求出，只是还要引入新的概念。

SAT问题长期未能找到确定的解题方法，是未能找到其特殊的结构规律造成的。子句消去法找到了CNF的结构特点，遵循首先确定变量唯一解，其次在变量普遍有2个可选解的情况下，确定出后续变量解，从而完全以确定的方式实现了CNF=1满足解的计算。

SAT问题是NP-complete类问题，按照学术界的观点，找到了SAT问题的多项式时间复杂度算法，就等于证明了NP=P。

本文的主题是介绍计算求出SAT满足解的方法，它适应任何SAT问题求解。关于子句消去法是否是O(nk+1)多项式时间复杂度算法，请参考文献[6]，本文不予讨论。

[1]P versus NP problem. https://en.wikipedia.org/wiki/P_versus_ NP_problem [OL].

[2]Cook S A. The complexity of theorem-proving procedures[C]// ACM Symposium on Theory of Computing. ACM, 1971:151-158.

[3]Stephen Cook. https://en.wikipedia.org/wiki/Stephen_Cook [OL].

[4]Boolean satisfiability problem. https://en.wikipedia.org/wiki/ Boolean_satisfability_problem [OL].

[5]姜咏江. 自己设计制作CPU与单片机[M]. 北京: 人民邮电出版社, 2014: 237-243.

[6]姜咏江. 论子句消去算法的多项式时间复杂度. http://blog. sciencenet.cn/blog-340399-1011907.html [EB/OL].

姜咏江（1945-），通讯作者，男，北京人，退休教师，中国计算机学会、中国电子学会高级会员。研究方向：数学、计算机科学。

Email: accsys@126.com

陈跃（1977-），男，北京人，西安交通大学博士，中国计算机学会会员。主要研究方向：大数据与机器学习、分布式计算。

Email: scottchen@163.com

A Fast Solution for SAT Problem based on Clause Elimination Method

JIANG Yong-jiang1, CHEN Yue2

(1. University of International Business and Economics, Chaoyang, Beijing,100013, China; 2. Xi’an Jiaotong University, Xi’an, Shanxi,710000, China)

Boolean satisfaction problem (SAT) is one of the fundamental problems that was proven to be NP-complete, which involves obtaining fast solution for various fields including integrated circuit design and optimization, biological gene, artificial intelligence and Internet. By using the concepts including Fix-bit number, Clause-block and Relate-section, a clause elimination method is discovered using the determination rule that aims at rapidly obtaining satisfied solution for SAT. A new way is found out for the solution of pure discrete variables.

SAT problem; Fix-bit Number; Clause Elimination Method; Clause-block; Relate-section; Polynomial Time Complexity

TP301.6；O158

A

2095-8412 (2016) 06-1255-05

10.14103/j.issn.2095-8412.2016.06.055