用方程(函数)思想审视一个问题的流行解法

四川省泸县二中 (646106)

廖兴建

用方程(函数)思想审视一个问题的流行解法

四川省泸县二中 (646106)

廖兴建

问题1已知1≤x+y≤2，-2≤x-y≤1，求5x-y的取值范围.

问题1是线性规划问题,用现行教科书的图像(几何)解法可解,除教科书的图像(几何)解法外,还有一个比较流行的二元函数值域法,即下面的解法1.

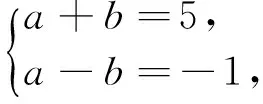
解法1流行，教师在教学中多数强调用此法，但也有用换元法求解.

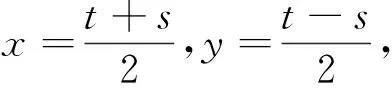
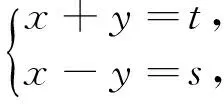
问题2已知1≤x+y≤2，-2≤x-y2≤1，求5x+2y-3y2的取值范围.

解:令x+y=t,x-y2=s,5x+2y-3y2=k,则x=t-y,y+y2=t-s,y2=t-s-y,所以,k=5x+2y-3y2=5(t-y)+2y-3(t-s-y)=2t+3s,即k=2t+3s(-2≤s≤1,1≤t≤2),求这二元函数值域得-4≤k≤7,即-4≤5x+2y-3y2≤7.

问题3已知1≤x+y≤2，-2≤x2-y≤1，求3x2+2x-y的取值范围.

解:令x+y=t,x2-y=s,3x2+2x-y=k,则y=t-x,x2+x=t+s,x2=t+s-x,所以,k=3x2+2x-y=3(t+s-x)+2x-(t-x)=2t+3s,即k=2t+3s(-2≤s≤1,1≤t≤2),求这二元函数值域得-4≤k≤7,即-4≤3x2+2x-y≤7.

问题3正确解法:令x+y=t,x2-y=s,3x2+2x-y=k,则y=t-x,x2=t+s-x,由关于x的方程x2=t+s-x有实解得1+4(t+s)≥0,所以,k=3x2+2x-y=3(t+s-x)+2x-(t-x)=2t+3s,即k=2t+3s(-2≤s≤1,1≤t≤2,1+4(t+s)≥0),就是方程、不等式混合组

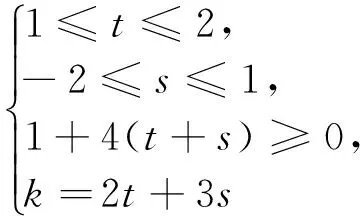
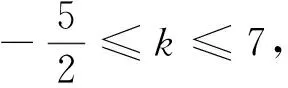
从上面的分析和正确解法可知,问题1的流行解法1是一个使用很有限的特殊方法,如问题1中稍加条件就是下面的问题.

问题4已知y≥0,1≤x+y≤2，-2≤x-y≤1，求5x-y的取值范围.

问题5已知x≥0,1≤x+y≤2，-2≤x-y≤1，求5x-y的取值范围.

很明显,用问题1的流行解法1解问题4,问题5得出的结果就不一定正确了.问题1的解法2通过换元产生方程,由方程发现问题并解决问题才是一个既自然,又简单的通法,问题1的流行解法1,由于不换元,就容易忽略进入方程(组)中的未知数的取值范围(因为表示实数的字母进入方程都有确定的取值范围,但比较隐蔽(即隐蔽条件),通过方程分离变量才容易发现并求出来(文[1],文[2],文[3]),也就容易出现错误.因此,换元产生方程(函数),使问题在方程(组),或方程、不等式混合组中,用最基本的方程(函数)的思想才能自然,本质的解决问题.

[1]熊福州.换元让问题进入方程,使本质暴露更完美[J].河北理科教学研究(河北)，2011,3.

[2]李 敏,熊福州.取值范围漫无边,全在方程函数中[J].中学数学研究(江西)，2012.

[3]熊福州.用方程思想深究一道选择题的病结果[J].数学通讯(上半月)，2013,4.