利用构造法解决极值点偏移问题

广东省大埔县虎山中学 (514200)

杨柳忠

利用构造法解决极值点偏移问题

广东省大埔县虎山中学 (514200)

杨柳忠

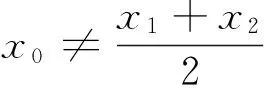
一、构造对称函数求解

1.实例探索

例1函数f(x)=(x-2)ex+a(x-1)2有两个零点.

(Ⅰ)求a的取值范围；

(Ⅱ)设x1，x2是f(x)的两个零点，证明：x1+x2<2.(2016年全国1卷理科数学第21题)

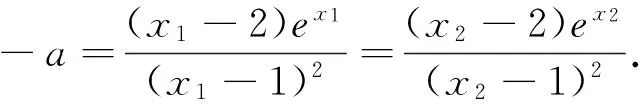
2.解法提炼

此法的几个关键步骤：

(1)构造一元差函数g(x)=f(x0+x)-f(x0-x)；

(2)对差函数g(x)求导；判断导函数的符号，确定g(x)的单调性；

(3)结合g(0)=0，判断g(x)的符号，从而确定f(x0-x)与f(x0+x)的大小关系；

(4)由f(x1)=f(x2)=f[x0-(x0-x2)]>(或<)f[x0+(x0-x2)]=f(2x0-x2),得到f(x1)>(或<)f(2x0-x2);

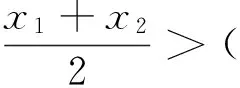
由于构造对称函数求解此类问题不需要复杂的变形技巧，可操作性很强，故而成为最一般的方法.其解题本质是比较x1与2x0-x2大小关系不方便时，转而通过比较与它们的函数值f(x1)与f(2x0-x2)的大小关系，再结合函数的单调性得到x1与2x0-x2的大小关系.

二、根据前一问的结论去构造新函数求解

1.实例探索

同例1，解：(Ⅱ)不妨设x1f(2-x2)⟺f(2-x2)<0.由于f(2-x2)=-x2e2-x2-(x2-2)ex2,f(x2)=(x2-2)e2-x2+a(x2-1)2=0,所以f(2-x2)=-x2e2-x2-(x2-2)ex2，设g(x)=-xe2-x-(x-2)ex,则g′(x)=(x-1)(e2-x-ex),所以当x>1时g′(x)<0,而g(1)=0,故当x>1时,g(x)<0,从而g(x2)=f(2-x2)<0，故x1+x2<2.

2.解法提炼

与第一个问的结论发生联系，把研究对象转化为证明某个新的不等关系，然后再构造新函数，利用新函数的单调性求解.这种办法应该更多是命题者出题的初衷，因为在学生现有的知识技能中就能解决，它不用再作一个复杂的，技巧性太强的构造，只要吃透了题意，把解决的对象恰当的转化一下，往往就能又快又准的解决此类问题.很多压轴题常常会设计好几个有梯度的小问，下一问的解决常常就要用到上一问的结论.

三、构造对数平均不等式解决

1.对数平均不等式

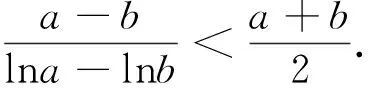
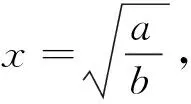
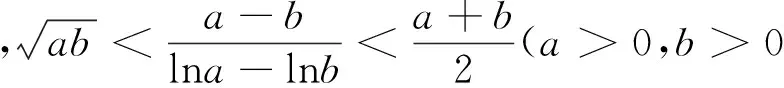
2.实例探索

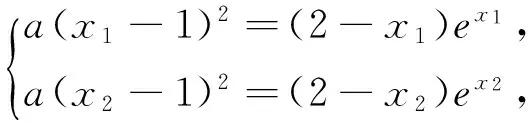
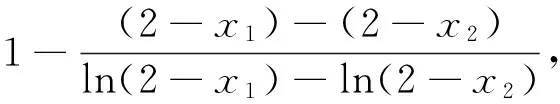
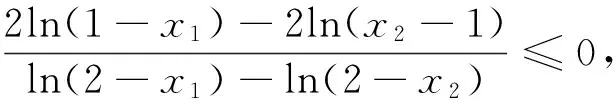
由对数平均不等式知

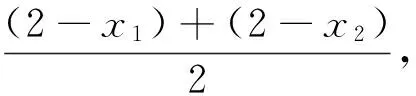
3.解法提炼

极值点偏移的问题，多数与指数函数或对数函数有关，此法的几个关键步骤：

第一步：根据f(x1)=f(x2)建立等式；

第二步：如果含有参数，则消参，如果等式中含有指数式，则两边取对数；

第三步：通过恒等变形转化为对数平均式，利用对数平均不等式求解.

四、利用换元法构造函数解决

1.实例探索

例2已知函数f(x)=lnx-ax有两个零点x1，x2,求证：x1·x2>e2.

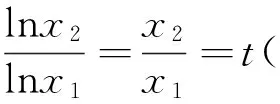
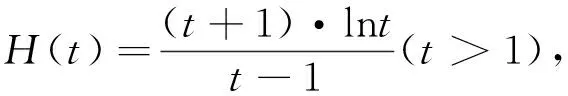
2.解法提炼

第二步：分析H(t)的单调性，利用函数的单调性求解.

以上四种方法各有优劣，不同的题目使用四种方法的简繁程度不一样，如例2使用前三种会显得复杂得多，而例1使用第四种方法确很难操作，我们应该根据题目的实际情况分析尝试，择优选择.我们发现极值点偏移问题归纳起来解法无非是构造函数与构造对数平均不等式，但它们同属构造，不同的题目构造的方式不一样，解法也就不一样，极值点偏移问题解法很多，题目也非常灵活，至于是否还有更佳，更美妙的构造，确实值得我们再深入去研究.

[1]郉友宝，极值点偏移的问题的处理策略[J].中学数学教学参考(上旬).2014(7)：19-22.