一道教材习题的解答分析、推广与应用*

四川师范大学数学与软件科学学院 (610068)

彭文强 邵 利 卢道燕

一道教材习题的解答分析、推广与应用*

四川师范大学数学与软件科学学院 (610068)

彭文强 邵 利 卢道燕

我们解完一道题就结束了，可能永远也体会不到解题的乐趣，因为数学题无限，永远也解不完.那么，我们只有细细回顾解题过程，才能收获更多.比如思考此题是否还有其他解法？变一变，该解法还能够解决吗？是否可以解决这一类题目，得到一般性的结论或方法？根据这样的想法，下面我们以一道习题为例来进行分析.

人教A版必修5教材第二章《数列》的总复习题中编排了下面这道习题(第69页第6题)：“已知数列{an}中，a1=5，a2=2，an=2an-1+3an-2(n≥3)，对这个数列的通项公式作一探究，能否写出它的通项公式？”

1 问题解答

问题1还有其他解法吗？

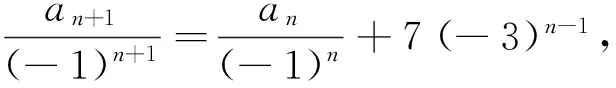
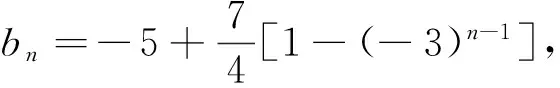
比较解法一与解法二：解法二计算量更小一些，并且相对不易出错，因此在此题中解法二相对要优于解法一.

问题2若将an=2an-1+3an-2中的“2”与“3”换成其他实数，会怎样呢？比如变为an=an-1+2an-2？

通过解答知道，根据上面的两种方法可以类似解出(这里从略，有兴趣读者可以解一解)，并且使用解法二同样要优于解法一.那么，

问题3若将an=2an-1+3an-2中的“2”与“3”换成任意实数“p”与“q”，会怎样呢？{an}是否一定存在？若存在，是否一定能够求出数列{an}的通项公式？下面我们用解法二对此进行探究(解法一从略，有兴趣读者可以解一解)：

2 问题推广

已知数列{an}前两项a1与a2，an=pan-1+qan-2(n≥3)(p,q为实数，q≠0)，求an通项公式.

分析：原题目实际上是把“-an-1”移到左边得到“an+1+an”，使右边刚好剩下3(an-1+an-2).对于一般的情形也可这样考虑，我们希望移“xan-1”到左边得到“an-xan-1”后，右边刚好剩下(p-x)(an-1-xan-2)，其中p,q满足x(x-p)=q，也就是说这里的x可根据这个方程求出.

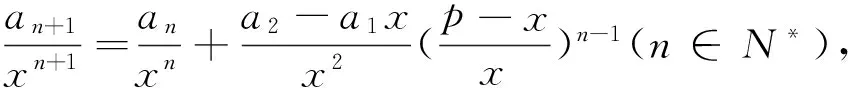
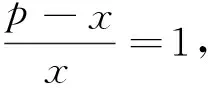
其中x,x-p为方程x(x-p)=q(即x2=px+q)的两根.于是我们可以得到：

推论已知数列{an}中前两项a1与a2，an=pan-1+qan-2(n≥3)(p,q为实数，q≠0)对应方程x2=px+q的有两根分别为x1,x2,若x1=x2，则；若x1≠x2，则).其中C1,C2为待定系数，可根据a1,a2求出.(注:这里的x1,x2可以为复数根，因此在复数范围内an一定存在；若只在实数范围内考虑，那么当x2=px+q无实数根时，这样的an就不存在)

这里我们通过探究问题3得到了更加一般性的结论，解决的方法就是一般性的方法.当然，我们得到一般性的结论后希望能够有所应用，下面举出三个应用例子.

3 应用

3.1 再解原问题

解：an=2an-1+3an-2对应方程x2=2x+3两根为-1,3，于是可设其通项公式为

an=C1(-1)n-1+C23n-1，由a1=5，a2=2知

3.2 求章头斐波那契数列通项

(人教A版必修5第26页)“有人说，大自然是懂数学的.不知你注意过没有，树木的分叉、花瓣的数量、植物种子的排列……都遵循了某种数学规律.你能发现下面数列1,1,2,3,5,8,13,21,34,55,89,…与这种规律的关系吗?”[1]

这里，我们可以利用推论求出它的通项公式.它的递推关系为an=an-1+an-2(n≥3)，其中a1=a2=1.

3.3 解高考题

这里我们只求{an}的通项公式.

这样，利用推广的结论解决原问题更加容易而简洁，也能够较为轻松地解决一些其他不同的问题.

[1]刘绍学等.普通高中课程标准实验教科书A版必修5[M].北京：人民教育出版社,2007.

* 本文由四川师范大学2016年研究生优秀论文培育基金项目资助(编号：20164-5).