也谈说题——一次“寻根之旅”

浙江省温州市第五十一中学 (325000)

鲍安戈

浙江省温州市温州中学 (325000)

刘旭飞

也谈说题
——一次“寻根之旅”

浙江省温州市第五十一中学 (325000)

鲍安戈

浙江省温州市温州中学 (325000)

刘旭飞

数学教师的基本功之一就是做题和说题.做题是教师的一种自觉修炼，说题是一种教学提炼.说题是指教师在精心做题的基础上，通过分析题目说清楚“如何审题”、“如何解题”、“如何反思”，总结解题策略，推广一般情况，从而归纳出经验性的解题规律.通过“做题、变题、追根溯源、推广”等一系列活动，将教师的“教”、学生的“学”与“考试命题”三者有机结合.

笔者曾参加了一次这样的活动，本文通过对参加这次比赛的实录，谈谈对如何“说题”的一点拙见，以期抛砖引玉.

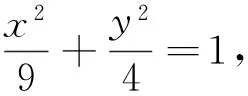
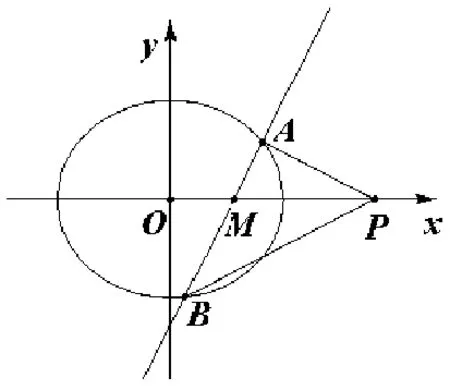
图1

(一)说题意

本题考查了椭圆的性质、直线与椭圆的位置关系等基础知识，考查运算求解能力、推理论证能力，考查转化化归思想、数形结合思想、函数与方程的思想、特殊与一般的思想.其深刻背景为：

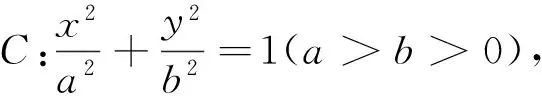
在解决问题的过程中，要求学生熟练地运用代数方法研究解析几何问题，在考查学生运算能力的同时，突出考查了学生的探究能力，对计算能力也提出了较高的要求，本题充分彰显了新课程的新理念.

(二)说解答

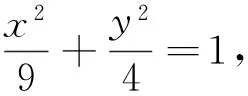
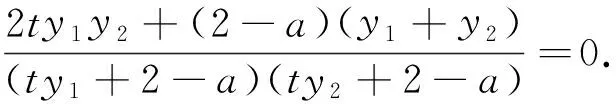
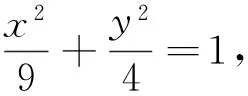
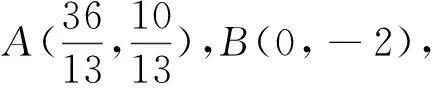
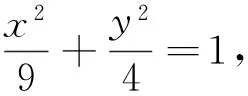
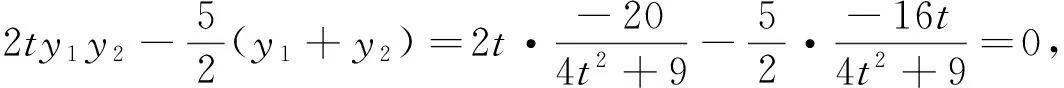
(三)说反思

本题是解析几何中定点问题的典型例题，对学生的要求比较高.此类问题的求解一方面要善于发现相关的几何特征；另一方面要充分体会函数思想、转化化归思想等思想方法在求解过程中的重要性.

解法1是解析几何问题中最常见的变量的选择方法，是学生首先掌握的基本方法，解法2是与斜率有关问题中变量的另一种选择方法，两种方法计算量都比较大.解法3通过特殊的直线，事先预测到定点，将求定点的问题转化为验证定点，不仅减少了变量，降低了计算量，而且使我们解题方向更加明确，目标清晰，提高了准确率.

(四)说思维

解析几何定值(定点)问题的常见策略有两种：

(1)常把变动的元素用参数表示出来，然后证明计算结果与参数无关，求出定值(定点)；

(2)可先取参数的特殊值探求定值(定点)，然后给出证明.

(五)说拓展

(4)背景逆命题也成立.如

(2013陕西卷理20)已知动圆过定点(4,0),且在y轴上截得的弦MN的长为8.

(Ⅰ)求动圆圆心的轨迹C的方程;

(Ⅱ)已知点B(-1,0)，设不垂直于x轴的直线l与轨迹C交于不同的两点P,Q,若x轴是∠PBQ的角平分线，证明直线l过定点.

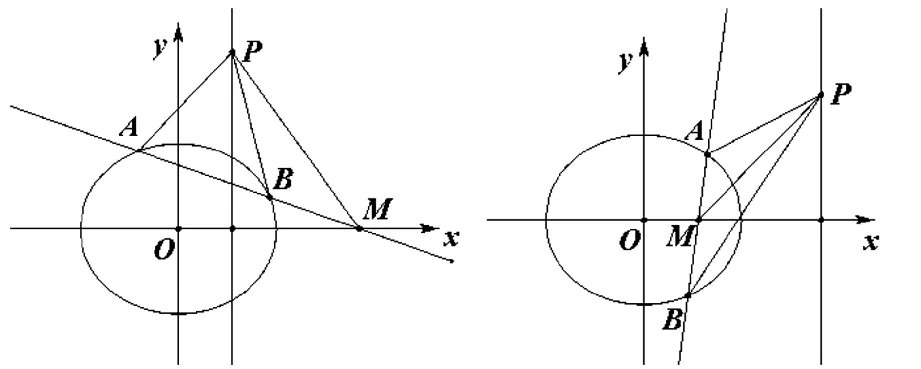
图2

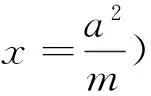
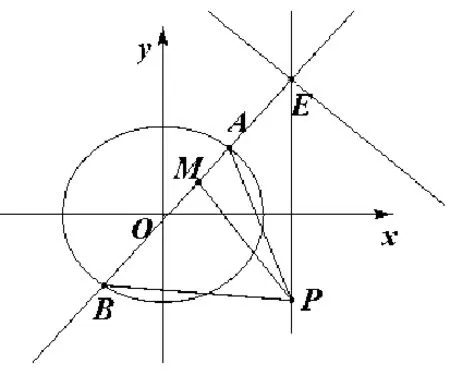
图3

(8)改变曲线：把椭圆改为双曲线或抛物线，上述结论仍然成立.

“题目小世界，思维大舞台”.开展说题比赛，不仅关系到教师自身素养的提高，也能提高数学课堂的教学效率.让研究试题成为高中数学教师的“自觉意识”，让说题成为高中数学教师交流解题心得的一个重要舞台.

高考题考查的知识大多是课本直接或间接涉及的内容，命题者往往把研究的路径藏于题外，若解题后不注重总结、提炼、挖掘，久而久之往往是广种薄收，题目稍加变化就不会了.感知知识的发生、发散、发展过程，明晰问题来龙去脉，寻求问题的解决方法，探究结论推广的可能，揭示问题的本质特征，是高三总复习的重中之重.每一个数学问题都有它的数学本质，面对难题学生解不出来往往是他们只看到问题的表层，无法深入到问题的内核，看不透问题的本质，那么教师在解题教学中就应该引导学生通过问题的解决揭示问题的本质，多探究善归类，给问题的本质一个“点睛”，使数学问题的解决变得简单而自然.