疏松砂岩储层窜流通道平面分布规律研究

于春磊，王硕亮，张 媛,3，王 娟

(1.中国石化胜利油田分公司地质科学研究院，山东 东营 257000；2.中国地质大学(北京)能源学院，北京 100083；3.中国石化石油勘探开发研究院，北京 100083)

疏松砂岩储层窜流通道平面分布规律研究

于春磊1,2，王硕亮2，张 媛2,3，王 娟2

(1.中国石化胜利油田分公司地质科学研究院，山东 东营 257000；2.中国地质大学(北京)能源学院，北京 100083；3.中国石化石油勘探开发研究院，北京 100083)

国内大部分高含水油田，注入水窜流现象较为严重，已成为影响油田高效开发的主要矛盾，对窜流通道形成后渗透率场的计算与描述显得尤为迫切和重要。目前窜流通道参数计算方法，只能计算得到注采井点的渗透率数值，不能计算得到注采井间的渗透率分布状况，并且目前窜流通道渗透率计算方法没有将室内实验结果、数值模拟结果和油藏工程方法结果有效结合起来。以国内某高含水油田为例，通过长期注水冲刷实验，模拟了窜流通道的动态形成过程，归纳出了储层岩石注水冲刷倍数与渗透率之间的关系式。在常规数值模拟计算方法的基础上，将渗透率变化规律模型引入到数值模拟计算中，建立了计算窜流通道平面分布的新方法。以海上某油田的地质模型为基础，计算得到了该油田目前状态的窜流通道渗透率平面二维分布规律。综合对比动态数据法、概率密度模型法、经验公式法和示踪剂测试结果，证明本方法得到的结果真实可靠。

窜流通道；渗透率变化；数值模拟；注水冲刷；参数计算

1 概 述

本文通过分析数值模拟过程中的流速场的计算原理，得到实际模型的累积注水倍数数据场。通过室内实验得到渗透率变化模型。将室内实验结果与累积注水倍数结果有机结合起来，达到利用已有数值模拟器计算结果刻画目前窜流通道渗透率的分布特征的目的。

2 考虑渗透率变化的数值模拟方法

常规数值模拟过程中，认为渗透率为常量，不随时间及其他参数进行变化。考虑到注入水冲刷对储层岩石性质改变的作用机理，需要在数值模拟过程中。对渗透率进行显式的修正，必须对差分和迭代过程的计算方法进行修改。目前常用数值模拟器都不支持这种处理方法，必须自行编写计算核心代码。

然而，自行编写计算核心代码带来了三个问题，第一，目前国内各油田都在推行油田管理数字化，有大量已经过历史拟合的数值模拟模型，这些数值模拟模型都是采用国际上公认的大型数值模拟器进行计算的。如果在窜流通道渗透率计算过程中，这些模型不能有效应用，将带来很大损失。第二，目前已有很多公开的数值模拟计算代码，但是这类计算程序多是用于科研计算，对复杂多变实际地质模型的适应性不强，很难达到整个油藏的顺利计算。第三，目前国际公认的大型数值模拟器能够很好地解决复杂地质模型的计算收敛性问题，但是核心算法部分是不对外公开的，自行编制的数值模拟器难以保证求解过程与国际公认的大型数值模拟器完全一致。如果产生了计算结果上的误差，新数值模拟器的可靠性不被认可，后期窜流通道渗透率的计算结果也难以令人信服。

因此，本文提出了一种可以利用已有数值模拟结果，计算窜流通道参数的方法。具体方法步骤为：(1)利用长期注水冲刷实验，得到具体实际区块岩心渗透率与累积冲刷倍数之间的关系。(2)分析常规数值模拟模型中每个网格累积注水冲刷倍数的计算方法。(3)将长期注水冲刷实验得到的实验数据带入到数值模拟器中，计算每一个时间步长的渗透率，最后一个时间步长的渗透率数据场即为窜流通道的二维展布规律。

微可压缩流体在各向异性、非均质地层中的流动方程为[8-10]：

(1)

式中：p.压力，MPa；x,y,z.三个方向坐标；t.时间，s；μ.流体黏度，mPa·s；qsc.第i个网格中流体标准状态的体积，m3；φ.孔隙度，f；c.压缩系数，MPa-1；B.体积系数，f；βc.传导率换算系数，f；αc.换算系数；k.渗透率，10-3μm2；Vb.总体积，m3。

首先利用数值模拟结果，输出每个网格各时间步长的水相流速。在数值模拟过程中，水相流速是一个中间计算步骤，在数值模拟器的后处理模块中不显示，但是在国内各大油田广泛应用的成熟商业化软件(如Eclipse，CMG等)能够输出水相流速，具体公式如下：

(2)

式中：Vw.水相流速，m/s；cl.液相压缩系数，f；i,j,k.x，y，z方向的网格序数；Δx，Δy，Δz.x，y，z方向的网格步长；Ax.垂直于x方向的横截面积，m2；Ay.垂直于y方向的横截面积，m2；Az.垂直于z方向的横截面积，m2；kx.x方向渗透率，10-3μm2；ky.y方向渗透率，10-3μm2；kz.z方向渗透率，10-3μm2。

得到每个网格水相流速后，与时间步长相乘，得到各个时间段的累计冲刷量，再将每个时间段的累计冲刷量求和，得到每个网格的历史累计冲刷量。

1.“市场布局优、盈利能力强”。在当前公司内外市场比重达到5∶5的格局基础上，加快对内外市场尤其是国际市场高端业务的占领扩张，进一步转变市场进入方式，多渠道参与市场竞争，不断开拓新的区域市场和新的服务领域。在盯住市场产值的同时，在成规模、创品牌、降成本上下功夫，努力提高市场创效盈利能力。

(3)

式中：t.时间步长，d；T.总时间长度，d；Ww.累计冲刷量，m3；

将每个网格的累计冲刷量除以每个网格的孔隙体积，可以得到每个网格的注入水冲刷倍数，根据对渗流方程在多维空间的离散化形式，每个网格的注入水冲刷倍数可写为[11]：

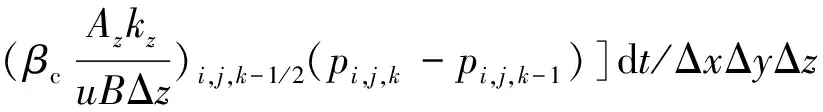
(4)

式中：n.累计冲刷倍数，f。

注入水主流线区域，注水冲刷倍数最高，渗透率变化速度最快，渗透率增加后，加剧了储层的非均质性，注入水会更加集中流经主流线，从而形成注入水的窜流。得到了累计冲刷倍数的计算结果，再结合渗透率随着累计冲刷量的变化模型，即可得到累计冲刷过后的窜流通道渗透率数值。

3 长期注水冲刷实验确定渗透率变化规律

目前发生注入水窜流的油田多属于高孔高渗的河流相储层，胶结疏松，长期注水冲刷后容易形成注入水窜流的优势通道，本研究以某海上油田的实际岩心为研究目标，设计了长期注水冲刷实验的流程，如图1所示。具体实验条件如下。

图1 长期注水冲刷实验实验流程Fig.1 Experimental process of long term water injection

实验温度：20 ℃；实验用水黏度，5 MPa·s；实验用油黏度，74 MPa·s；实验用水矿化度，4 500 mg/L；实验岩心为南区NmI3层天然岩心。岩心参数如表1所示。分别选取渗透率数值3 000×10-3μm2、3 500×10-3μm2和4 200×10-3μm2的岩心各8块，总共24块岩心。

表1 实验用岩心参数

具体实验流程为：①将岩心进行渗透率测定；②烘干、称重、饱和地层水；③油驱水造束缚水；④恒速驱油，连续驱替一定的孔隙体积；⑤将岩心洗净、烘干，测定试验后岩心渗透率。

通过计算不同注入倍数前后的渗透率变化，绘制了注入水倍数与渗透率变化曲线，如图2所示。

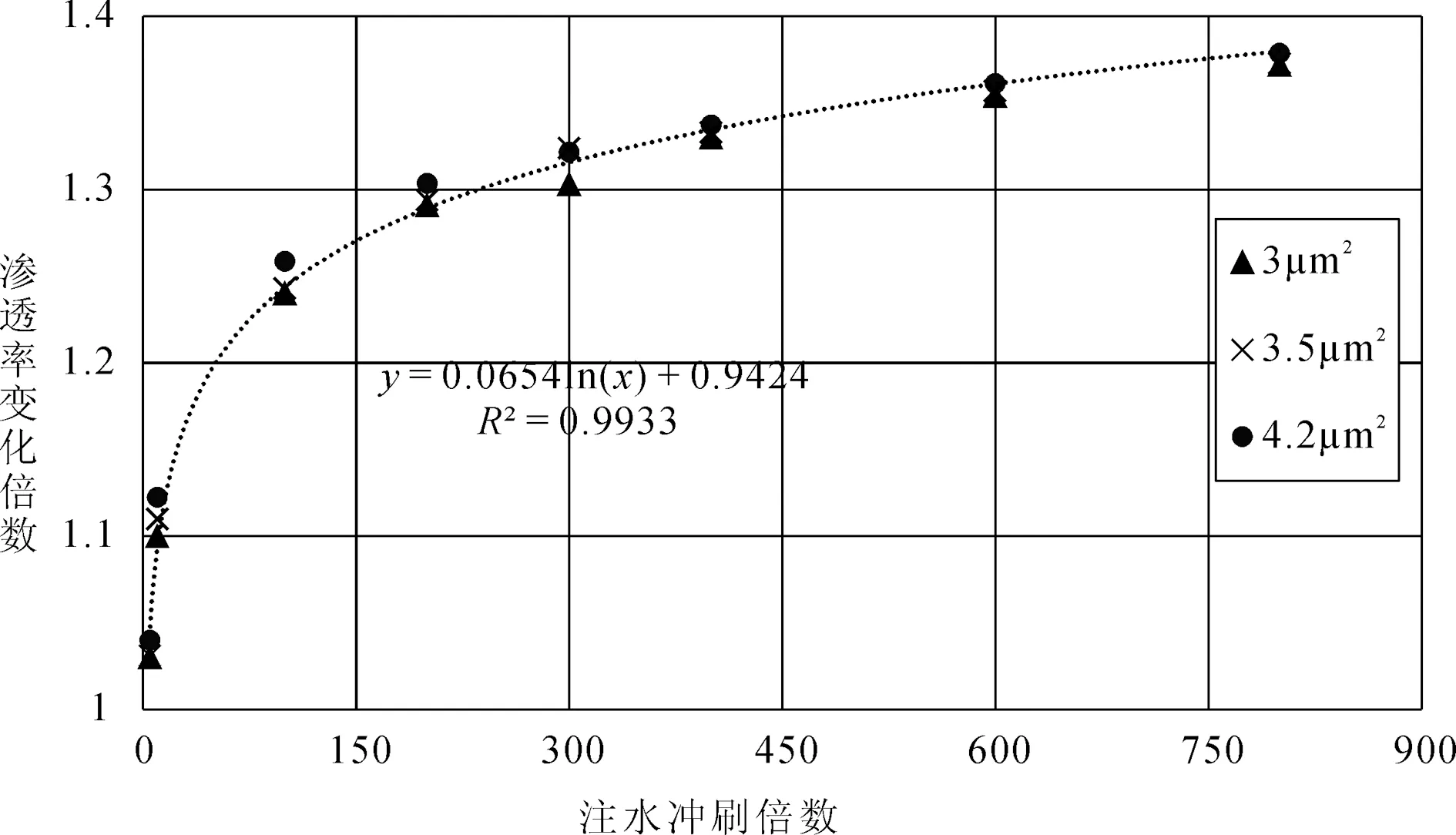
图2 不同注入水倍数渗透率变化曲线Fig.2 Permeability change curve with different injection water volume

渗透率主要受岩石微粒、孔隙半径、胶结物等因素的影响。长期注水冲刷作用对渗透率的影响取决于注水对岩石孔隙结构的改变，地层微粒被水从孔道中冲出来，使孔喉半径增大从而渗透率增加。通过拟合注入水冲刷倍数与渗透率变化倍数之间的关系，得到了海上某油田南区NmI3层的渗透率数值变化模型为：

mk=0.065 4lnn+0.942 4

(5)

式中：mk.渗透率变化倍数，f；n.注入水冲刷倍数，f。

4 计算结果与验证

综上所述，窜流通道参数计算的方法和流程如下。

(1)选择具有代表性的实际岩心，开展长期注水冲刷实验，利用注水冲刷倍数与渗透率的测试结果，建立渗透率与注水冲刷倍数的函数关系。

(2)将渗透率与注水冲刷倍数的函数关系，带入到数值模拟器的计算方法中，得到渗透率随时间变化的数值。

(3)利用公式(4)，对第一个时间步长的累计注水冲刷倍数进行计算，将计算结果带入到渗透率与累计注水倍数函数中(公式(5))，得到下一个时间步长的渗透率数值，逐步循环迭代，得到目前状态的渗透率数据场。

选择海上某油田南区NmI3层为研究对象，建立三维地质模型，利用本文建立的窜流通道渗透率计算方法，进行窜流通道参数计算。累计冲刷量的计算结果和累计冲刷倍数结果如图3所示。

利用公式(3)计算累计注水冲刷量，计算结果如图3中(a)所示。利用公式(4)计算累计注水冲刷倍数，计算结果如图3中(b)所示。将每一个时间步长的累计注水冲刷倍数，带入到公式(5)中，进行数据场运算，逐步迭代，可以得到目前储层渗透率，计算结果如图4所示。

图4中(a)为海上某油田初始状态渗透率分布场，(b)为海上某油田目前状态渗透率分布场。通过分析原始渗透率与目前渗透率分布场可以明显看到：随着注水时间的增加，渗透率整体呈现逐渐增加的趋势，原始的高渗透区域与目前的高渗透区域相比有所变化，渗透率变化明显的区域主要分布在累计冲刷倍数较大区域。目前渗透率较高的区域呈现纺锤形特征，主要分布在注入井与生产井的井底附近，在注采井间，由于流线的发散，累计注水冲刷倍数较小，渗透率变化也较小。

图3 累积注水冲刷量计算结果(a)和累积注水冲刷倍数计算结果(b)Fig.3 Results of cumulative water injection (a) and results of cumulative water injection multiple (b)

图4 海上某油田NmI3层原始渗透分布图(a)与目前渗透率分布图(b)Fig.4 The original permeability distribution map (a) and current permeability distribution map of NmI3 layer in an offshore oil field (b)

为了验证目前渗透率场是否能够准备表达目前的窜流通道渗透率，将本文计算得到的结果与目前主要的窜流通道渗透率计算方法(动态数据反算法[12]、概率密度法[4]和示踪剂解释[13])的结果进行对比，如表2所示。

表2 窜流通道渗透率解释结果对比表

Table 2 Comparison of permeability interpretation results of channeling

水井油井本文计算渗透率/μm2动态数据反算法/μm2概率密度法/μm2示踪剂解释/μm2C13C07792766717703C15C12892666930853C21C23851688930824C21C321106129215621120D05D018031082760826D05D249367077501025D16C091056100710931120D16C246146521497780D16D1381673855912

通过对比4种方法的计算结果，发现4种计算结果的符合率较高，本文建立的窜流通道参数计算方法的计算结果与示踪剂解释结果最为接近。2010年11月对D16井组进行了氮气泡沫调驱，2011年1月对C21井组进行了微球调驱[14]，增油效果明显，进一步说明本文建立的方法的准确性。

5 结 论

(1)利用海上某油田南区NmI3实际岩心，进行了长期注水冲刷实验，回归得到了储层渗透率随着注入水倍数的变化模型。

(2)对已有数值模拟方法进行修正，将室内实验得到的渗透率变化模型引入到数值模拟计算中，建立了用于计算窜流通道渗透率的新模型。

(3)建立了海上某油田南区NmI3层的三维地质模型，利用本文方法对该区块的窜流通道平面分布规律开展分析。并综合运用动态数据法、概率密度模型法和示踪剂解释结果，与本文计算得到的结果进行对比验证，说明本文计算结果较为可靠。两个井组的调驱措施的成果，进一步验证了本文提出计算方法的准确性。

[1] 叶翠.高含水油田井间动态连通性研究[D].武汉：长江大学，2013：10-20.

[2] 陈民锋，姜汉桥，朱龙权.水驱砂岩油藏注采窜流井区判别研究[J].复杂油气藏，2011,4(1)：46-49.

[3] 刘同敬，姜宝益，刘睿，等.多孔介质中示踪剂微观可视化实验研究[J].断块油气田，2013,20(4)：530-534.

[4] 姜汉桥，刘奋，洪光明，等.用概率模型方法确定卞东油田高渗通道地质参数的研究[J].石油勘探与开发，1997,24(1)：55-58.

[5] 郑强，刘慧卿，李芳，等.油藏注水开发后期窜流通道定量识别方法[J].石油钻探技术，2012,40(4)：92-95.

[6] 刘卫，林承焰，杨永智，等.低渗透厚油层层内优势窜流通道定量识别新方法研究[J].石油天然气学报，2010,32(1)：1-5.

[7] 冯其红，齐俊罗，尹晓梅，等.大孔道形成与演化过程流固耦合模拟[J].石油勘探与开发，2009,36(4)：498-502.

[8] ISHIBASHI T, WATANABE N, HIRANO N, et al.GeoFlow: A novel model simulator for prediction of the 3-D channeling flow in a rock fracture network[J]. Water Resources Research,2012,48(7):259-281.

[9] TSOFLIAS G P, PERLL C, BAKER M, et al. Cross-polarized GPR imaging of fracture flow channeling[J]. Journal of Earth Science, 2015,26(6)：776-784.

[10] WANG S, JIANG H, LI J, et al. The prewarning of profile modification method in a high water Oil Field[J]. Petroleum Science & Technology, 2012,30(22):2383-2392.

[11] WANG S, JIANG H. Determine level of thief zone using Fuzzy ISODATA clustering method[J]. Transport in Porous Media, 2011,86(2):483-490.

[12] 冯其红，史树彬，王森，等.利用动态资料计算大孔道参数的方法[J].油气地质与采收率，2011,18(1)：74-76.

[13] 赵继龙，王俊鹏，刘春，等.塔里木盆地克深2区块储层裂缝数值模拟研究[J].现代地质，2014,28(6)：1275-1283.

[14] 吴永彬，张运军，段文标.致密油油藏空气泡沫调驱机理实验[J].现代地质，2015,29(6)：1315-1321.

Study on Two Dimensional Channeling Distribution of Unconsolidated Sandstone Reservoir

YU Chunlei1,2，WANG Shuoliang2，ZHANG Yuan2,3，WANG Juan2

(1.Research Institute of Exploration and Development of Shengli Oilfield Company, SINOPEC, Dongying, Shandong 257000，China;2.SchoolofEnergyResources,ChinaUniversityofGeosciences,Beijing100083,China;3.SINOPECPetroleumExploration&ProductionResearchInstitute,Beijing100083,China)

The injection water channeling phenomenon is more serious in most of the high water cut oil fields. The injection water channeling phenomenon has become the main contradiction in the effective development of the oil field. The channeling formation permeability calculation and description method are particularly urgent and important. At present the channeling permeability calculation methods can only calculate the channeling permeability at injection and production well point, can’t get the channeling permeability distribution between injection production wells. The calculation method is relatively isolated, and there is no effective combination of the experimental results, the numerical simulation results and the reservoir engineering method results. In this paper, through the long-term water injection experiment, the dynamic formation process of the flow channel is simulated. And the relation formula between the water injection erosion ratio and the permeability of the reservoir is concluded. On the basis of the conventional numerical simulation method, the permeability variation law model is introduced into the numerical simulation calculation, and a new channeling distribution of unconsolidated sandstone reservoir is established, and the two dimensional distribution of permeability in the current state of the oil field is obtained. By comparing the dynamic data method, the probability density model method, the empirical formula method and the tracer test results, the results of this method are proved to be reliable.

channeling; permeability variation; numerical simulation; injection water flooding; parametercalculation

2015-11-10；改回日期：2016-03-20；责任编辑：孙义梅。

国家自然科学基金项目(51504223)；中国地质大学(北京)基本科研业务费专项资金资助项目-优秀教师基金项目(53200859060)。

于春磊，男，高级工程师，1984年出生，油气田开发专业，主要从事油藏物理模拟研究。Email：yuchunly@sina.com。

TE311

A

1000-8527(2016)05-1134-07