图学与几何

何援军

(上海交通大学计算机系，上海 200240)

图学与几何

何援军

(上海交通大学计算机系，上海 200240)

本文讨论图学与几何的关系。从形是图之源、图形/图像的本质是几何这个基本认识出发，指出图的产生、表示、处理与传播过程都是在处理几何的定义、变换与其间关系，因此图与图学的基础是几何，图学计算的基础是几何计算。基于图学与计算的内涵分析，剖析了图形计算的本质、矛盾和关键技术。讨论了代数与几何在图学计算中各自的作用与利弊，强调人在算法设计中的主导地位。指出生成一幅图或构建一个模型的主要工作不是决定构成该图或模型的元素本身，而在于找出元素之间的相互关系。针对图形图像已经成为计算的主要对象与结果表述，介绍了一种基于几何的形计算机制，弥补常规数计算的不足，追求“形思考、数计算”的几何计算新模式。

图学；几何；几何计算；数计算；形计算

这是关于图与图学的第六篇文章[1-5]，这次讨论图学与几何——这两门科学的关系。

何谓科学？给科学一个充分的、本质的定义并非易事，因为科学其实是一种社会的、历史的和文化的人类活动。科学首先是对应于自然领域的知识，经扩展，引用至社会、思维等领域，如社会科学、自然科学和思维科学等。科学是知识，且不是零碎而是理论化、系统化的知识体系，是人类对自然、社会的认识活动。

图学已经是这样的一门科学。图形的形象性、直观性、准确性和简洁性使得人们可以通过图形来认识未知，探索真理，图形/图像在人们生活中的应用已经极大的普及。图形/图像已成为重要的计算对象与计算结果，已被作为解的一种表现形式去追求，不管是静态的或者是动态的，这样的计算，遍及各个领域。人类社会已经进入一个图形/图像时代。统一图形/图像的研究顺应了这个形势，符合图形/图像发展的规律，图与研究图的图学科学的作用将会日益增大。

本文阐述图学理论化、系统化的知识体系，梳理图形/图像的表达机制与产生机理，指出图形/图像的源头是形，基础是几何，由此认识图学与几何的关系。从图形/图像的本质入手，分析图学计算的若干关键问题，揭示图学计算的内涵，从计算与几何两个关键问题出发，分析了图学计算的基础，讨论了代数与几何在图学计算中各自的作用与利弊，这决定了图学计算模式的选择。最后，本文依据图学计算的对象和目标是图形/图像，介绍一种“形计算”机制，研究从形的整体去主导算法设计，构建算法框架；阐述形计算在计算中的地位、作用和应用领域，给出其理论基础、计算基础和实施方案及实例。这是几何代数化发展到图形/图像时代的必然趋势——加强图形认知方式在计算中的作用。

1 图与图学

1.1 图形图像

文献[6]指出，图(graph/picture/graphical images)实际上可分成“图形类”和“图像类”两种。

图形类(drawing or wire frame)，以矢量图形式呈现，在计算机中由场景的几何模型与物理属性表示的图形，能体现景物的几何个体，记录体元的形状参数与属性参数。例如，工程图纸(drawing)，最基本的图形单元(简称“图元”——primitives)是点、线、圆/弧等，其信息包含图元的几何信息与属性信息(颜色、线型、线宽等显式属性和层次等隐式属性)。

图像类(image/bitmap)，以点阵图形式呈现，在计算机中以具有颜色信息的点阵来表示的图形，其更强调整体形式，描述一个个点——像素(pixel)或图像单元(pels，picture elements)，记录点的几何位置及它的灰度或色彩，如照片、扫描图片和由计算机产生的真实感、非真实感图形等。其信息实际上是点与它的属性信息(颜色、灰度、亮度等)。

因此，本质上图形和图像都是带有属性的基本几何的组合。

图形，由“图”和“形”两个字组成，其实这里至少有两层意思：其一，图描述形，是形在画面上展现，去展现形，是形的载体；其二，图源于形，由形而来，形是图之源。在计算机上模拟现实世界、构建虚拟世界，先要造型，而后得图。形是对现实的模拟和构造，其属性是表示、是输入；图是形在画面上展现，其属性是表现、是输出。它们的共性元素是几何。可以用“图”一词，从“形”的角度去统一图形/图像的表述，研究图形/图像的表示、产生、处理与传输理论和方法。

1.2 图学(graphics)

图乃万物之现，与宇宙同生并存，承载人类文明，展示人类文化，叙述苍穹之变化，记录文明之发展。图书图书，左图右书。对图形作为计算源与计算结果的需求大大增加。图的学科不仅仅是“工程图学”，已经发展到“信息图学”、“科学图学”乃至“生活图学”等等。

现有关于图的科学主要有工程图学、计算机图形学和计算机图像处理。

工程图学作为工程与技术科学基础学科，是发展最早，理论与实践也最完善的图学学科。其现在面对一个新的现实，计算机的介入改变了原先的制图工具，制图过程中人的思维与计算机图形软件两个终端的直接连接使工程图学处于一个尴尬境地。但是，图纸作为工程语言的地位没有改变，制图、读图、图纸的信息共享等的理论、方法与技术需要工程图学去承担。

计算机图形学现在地位稳固，几乎所有领域都可涉及，新的理论、方法乃至硬件日新月异。这就需要静下心来思考，计算机图形学最基础、最本质的是什么？图的生成与处理应该是计算机图形学的核心内容，在计算机图形学中讲造型，处于服务于绘制的地位，是可以选择的内容。

计算机图像处理包括对数字图像的处理、对数字图像的分析与理解、数字化图像的采集，以及对图像处理结果的数字化表达等。计算机图像的本质是平面上的点以及点的属性(颜色、灰度等)，因此其理论可以分成两个部分：对密集的点的处理和对色彩的处理。

IEEE对计算机图形学的定义是：Computer graphics is the art or science of producing graphical images with the aid of computer，这个定义有几个关注点：首先，定位计算机图形学不仅是一门科学，还是一门艺术；其次，虽然认为图像借助于计算机但没有提及从何产生？

由于计算机的介入与发展，图形与图像在计算机上的表示已逐渐趋于统一，研究图形、图像科学的发展也已经到了几乎彼此不分的地步。社会已经进入到一个在“大图”与“大图学”概念上研究图与图学的历史新阶段。统一图形、图像的研究顺应了这个形势，符合图形、图像发展的规律。

中国图学学会在2013年发布图学学科报告[1]，给图学下的定义是：“图学是以图为对象，研究在将形演绎到图的过程中，关于图的表达、产生、处理与传播的理论、技术与应用的科学”。这个定义的主要论点是：图学研究形和图的表示、表现以及互相关系，其基本内容包括：造型、由形得到图、图的处理、由图得到形以及图的传输等。这里，目标是图、核心是形、本质是几何，基础是几何计算。图学的理论、方法和技术的主要基础是几何学及代数学，也借助于其他学科或学科交叉。其首次揭示了形是图之源，并统一了图形图像的称谓，合并称图，建立了大图和大图学的概念。这个定义也反映了图、图学与几何的关系。

2 图学与几何

2.1 图学的本质是几何

James R. Miller[7]说过：Computer graphics and modeling rely on mathematical operations on points and vectors. I advocate using vector geometric analysis to simplify required derivations，短短两句话，揭示了计算机图形学和造型的基础是点与向量的运算，充分认识到了图学与几何的紧密关系。国际学术组织International Society for Geometry and Graphics (ISGG)，每 2年召开一次 International Conference on Geometry and Graphics，这是将图学与几何定位得最紧密也是最贴切的国际学术组织与国际会议。

图学研究将形演绎到图，以及图的表达、产生、处理与传播。图源于形，由形而来，在计算机中，形与图都是由几何构造与描述的，这里的几何是点、线、面等，可被称为“几何元”，这些不同的几何元依照一定的拓扑关系组织起来构造成不同的几何形体；通过投影在平面显示成图——图形或图像，此时，点、线被称为“图元”，图元是具有不同属性的几何元。因此，不论是位图还是矢量图，终极处理对象是点、线等几何元。它们都源于几何。表1给出了几何计算在计算机图形学中的作用，几何与几何计算在图学中的地位和作用可见一斑。

表1 几何计算在计算机图形学中的作用

在学科分工上，计算机图形学与计算机图像处理各有侧重，计算机图形学偏重于从形得到图，计算机图像处理则偏重于对图本身的处理。尽管图形与图像的处理方式存在差异，但是其计算基础是相同的，同是几何。

计算机图形学中的两个典型算法隐藏线消除算法与真实感图形绘制算法可以很好的说明其同一性。隐藏线消除是将形显示为图形的典型算法，消隐过程是一条一条线的输出，每条线需与场景中所有可能遮挡它的物体(面)进行比较，线的各可见部分的交集即为此线的最终可见部分。真实感图形绘制则是将形显示为图像的典型算法，这是一个基于光强与色彩的量化、纹理映射、图像合成、帧缓存等基于物理、光学、色彩理论的复杂计算过程。两个算法在三维空间的主要计算都是从光源发出的每一条光线与景物表面的空间线面的求交与分割计算，计算的目标都是为了求得空间点，消隐计算是2个点，光照计算是1个点。只是在最后的显示阶段，其才各走自己的路，一个取2个点得到线段及线的宽度、线型、颜色等属性，组成图形；另一个则去计算1个点的色调、色饱和度和亮度等属性，得到像素，组成图像。这里，算法研究的重点与主要的计算工作都在几何求交、几何分割和几何比较等几何计算上。

在计算机图像处理领域，在基于剪影轮廓三维重建中，通过空间线段的求交计算获取构成可视化外壳的公共线段集合是核心步骤。声称空间线段求交计算在整个重建流水线耗时约占整个建模时间的 30%～40%，目前求交运算的速度还是该技术在速度方面的瓶颈之一[8]。

最后，图学计算中常用的几何变换、图形变换和坐标系变换也是与几何密切相关的。平移、旋转、比例以及投影(正投影或透视投影)等，这些变换都是几何变换，可以用变换几何化方式实现。

2.2 图学计算中的若干问题

2.2.1 图学计算的本质是求取几何间的关系[3,9-11]

图形/图像的基础是几何。几何由一系列几何元按照一定的几何关系构成，少数基本几何元根据不同的关系就可组合出万千几何。例如，给出平面上不重叠的4个点，这4个点可以构造C42=6条线，这6条线可以组成∑C6i(i=1, 2, 3, 4, 5, 6)个不同的图形。在空间，更要指出哪2个点构成了一条线，哪些线围成了一个面，哪些面构成了一个形体等等。可见，主导形表示的是几何元间关系而非几何参数。在用两个形体产生一个新模型时，难点也在如何根据参与运算的那些源去重新构建一个几何间的新关系，而且这个新关系的组织远比只通过几何间的求交就可得到几何参数的计算困难得多。这背后显现出的另一个问题是：几何计算不仅仅是“计算”，还有一个“表示”问题。

2.2.2 维度差距的矛盾

图学计算过程中，存在多种空间维度的不统一问题。

(1) 实体空间与表示空间不统一。不管是“立体图”还是三视图，看到的图都是二维的，是用二维表示三维的。因此，实体空间(三维)与表示空间(平面)是不统一的。

(2) 思维空间与计算空间不统一。形是空间的，代数计算是线性的。几何代数化将对几何的图形认知转化成基于参考系的数字表述形式，三维的形被直接跨越到一维的数，缺少必要的过渡和衔接。几何属性被打得面目全非，形的关系和变化难以完备获得和表达。人的空间思维优势难以发挥，对算法的掌控能力下降。遗憾的是，人们似乎常常忽视这些空间不统一的矛盾，长期以来人们大多使用这样的方式——“用一维计算处理二维甚至三维问题”。人们习惯于这样的复杂！数学机械化[12-13]就公开宣称，其工作就是“把质的困难转化为量的复杂”。

2.2.3 算法稳健性的不可控

现在的算法研究常出现两个偏向，一是只偏重速度而忽视稳定性(robustness)，偏重速度的研究方法只是减少了浮点运算，是令人担心的。二是采用一些大规模没有理论分析的随机测试去验证算法的稳定性，很难检测到影响算法的特殊状况[14]。

模型通常是有界的，例如不是直线而是线段或向量、不是平面而是多边形等。模型的有界造成几何间的特殊关系(共点、共线、共面)，形成几何奇异，其错误对几何计算稳定性的冲击是根本性的[9-11]。

几何体在浮点运算环境下的表示是不精确的，几何计算也是近似的。需要从构造的角度阐述几何奇异的几何本质，认识几何奇异的根本性，在检测与处理两个层次，准确界定几何位置的奇异界线，保证几何奇异的正确判定、准确检测，从理论上构筑一个几何奇异问题的完整解决方案。

2.3 计算基础

数学是研究“数”与“形”的科学，代数是研究“数”的学科，几何是研究“形”的学科，几何与代数的概念及方法都是研究科学和工程问题的重要数学工具[15]。几何涉及的是空间问题，几何从空间概念形象地审视问题，常用几何间的相互(空间)关系处理问题，人们努力将一些问题归结为几何形式，因为这样可以使用人的直觉，直觉是人类最有力的武器。代数涉及的是时间的操作，采用线性、有序的方式去处理问题。代数的目标总是想建立一个公式，就是拿来一个有意义的东西，将其化成一个公式，然后得到答案。代数计算时本质上不会再思考其含义，停止用几何、图形或物理的观念去考虑问题。

数学上主要有两种推理：符号推理与直观推理，前者源于计数制，后者源于图形制。继数之后，形作为数学的第二个主要概念被引入，形能充分发挥人的空间思维特长。欧几里得在几何著作中首次系统地使用了形，少量使用符号，大量使用逻辑。他的著作结合了两种创新：图形的使用和证明的逻辑结构。

数学科学发展的历程中，几何与代数原本分别考虑“形”和“数”的问题，各有自己的发展空间和问题域，也各有自己的理论基础和方法学，理论上应该各占半壁江山，各司其职。然而，历史并不是这样，两者并不平衡。17世纪初，Descartes(笛卡儿)将坐标引入几何，把代数中形式化符号体系的表示方法引进到几何学中，使得几何间的计算也能用代数形式实现，几何(形)的概念用代数(数)表示，人称“几何代数化”[16]，这是数学史上最丰富和最有效的创造之一。之后，形势变了，代数与几何之间出现了一种令人感到不太自然的关系。在笛卡儿“一切问题可以化为数学问题，一切数学问题可以化为代数问题，一切代数问题可以化为代数方程求解问题”思想的统治下，使得代数基本上取代了经典几何的地位。

在几何的大家族中，有一个不为人注意的分支——画法几何(descriptive geometry)[17]，现在几乎没有人将画法几何列入几何的范畴。其实，画法几何研究的基本对象也是几何，也是研究形的科学。17世纪一些几何学家将其方法与结论视为欧基里德几何学的一部分，直到 1799年法国几何学家蒙日(Gaspard Monge，1746—1818年)非数学地阐述了投影理论，使画法几何成为一门独立学科。画法几何以“正投影”理论为基础，通过投影将空间物体转换成平面图形，引导人们在平面上去虚构三维物体，解读三维空间。由于维数的降低导致信息的缺失而需要多个视图表述三维物体，引发“2D/3D对应”理论的出现，它是将视图“还原”成三维物体的理论基础。三维物体化为平面问题以后，平面图形基本上只要考虑点、线、圆等基本几何元素，“尺规作图”方法使少量的作图工具和方法就可作出大部分平面图形。至今，画法几何在空间形体的表述、几何问题的求解方法上仍然保留了几何的方法，这似乎更接近于人的图形认知模式。

模型的表述与构造，图的产生与处理，进行这些工作的都属于图学计算的范畴。图学计算的对象和结果是形、图形和图像，所以，图学计算有其独特的矛盾和特别需要解决的问题，只有看到和分析清楚这些问题，才能有的放矢地研究和探索图学计算的理论与方法。

2.4 图学计算的模式选择

(1) 计算是一切的基础。在人类的社会进步、经济建设和科技发展过程中，“计算”始终都扮演着非常重要的角色。“X计算”已是计算机广为应用的一个概念，例如，科学计算、网格计算、平行计算、智能计算、云计算等，几何计算是其中之一。几何计算是科学与工程计算的基础与支撑，在计算机图形学、计算机辅助设计与制造、计算几何以及医学图像处理、建筑设计、运动学与机器人等领域有重要作用与应用。

(2) 计算的学问应该叫“算学”。其实，算学一词很有特色，其抓住了计算的本质，更能体现计算的神韵，又有动态感。而且，从某种意义上说算学的范围似乎比数学的大，例如，在计算机时代，至少算学还包括算法。Mathematics在中文中对应的是“数学”这里的“数”不是 Data、Digital等，而是Calculate、Compute、Consider、Analysis和Plan等，是Arithmetic。在计算机时代，更应包含Algorithm。计算对象可能并非一个，结果也不一定是一个，甚至是不确定的。

(3) 计算的基础是数学。人们对计算及其结果的基本要求是快速而直观，是一个(组)简单的数字，或是一幅(批)合适的图。因此，表述计算的对象与结果只有2种：数和形，数和形又分别对应于数学的2个基础学科——代数与几何，对应于数计算与形计算。

数学是永恒的！好的数学思想很少会过时，虽然运用方式会发生很大变化。

(4) 算法的关键在于设计与模型构建。对一个问题求解的一般过程是：提出问题→建模表达问题-使问题抽象化→用一个几何模型去表示问题→将几何模型生成图形/图像→使问题可视化→根据生成的图形/图像进一步理解问题、思考解决方法。因此，在几何计算的算法设计中，设计与模型是引领性、整体性的，如同有一个“形”的整体始终贯穿于整个求解过程，正是这个“形”使人的图形认知能力在算法的设计过程中得到最大的发挥，保证人在几何计算中的掌控地位。

(5) 数计算的一些缺陷需要暂且搁置。数计算求解过程的不直观使得人的空间思维特长荡然无存，计算常变得不可读，甚至不可掌控。史蒂芬·霍金有一句名言：Some told me that each equation I included in the book would halve the sales. I therefore resolved not to have any equation at all (有人告诉我，我在书中的每一个方程都会使这本书的销量减半，为此我决定一个方程也不用。)[18]足见代数的不可读性对交流的杀伤力。还有一些问题困扰着纯代数方法，如不必要的复杂度、需要较复杂的数学计算工具、算法时间性能低下、无法完美处理奇异性问题等等。

(6) 目前的几何计算方式过于依赖于数计算。随着计算机科学的发展，许多计算的对象都是图形和模型，结果也以图形/图像的形式呈现，其主要元素是几何或形。由于一般的计算都是采用数计算机制，这样，几何计算的过程就变得有点复杂：【形→数】→【数计算】→【数→形】。这样，人的大量工作就会花在【形→数】和【数→形】的转换上，这不符合人的思维习惯。其实，数学主要发生于幕后，起关键作用的是人，人的思维、人的逻辑。所谓“交互”，就是人与机器的相互作用。交互系统的产生，就是充分考虑了在计算机快速中发挥人的直观感知能力的作用，这是一个很大的进步，是人机结合的典范。

(7) 在几何计算中更充分发挥几何特性。几何的本质是某些属性不依赖于参考坐标系，具有不变性，这是研究几何的基础。面对一个几何问题，是首先考虑如何将它化成一个代数方程(公式)，送到计算机里，摇一摇就得到结果，而不管过程如何复杂；还是充分发挥形与数各自的优势，先从空间的角度审视一个几何问题，借助于图形的直观，用几何的思路寻求一个全局、直观的解决方案，将枯燥的数字与反复的的代数计算分离给计算机去做，发挥人的直觉优势，回归人的主控地位，一改数百年来的几何代数之路。长期以来，人们总以几何代数化这样的思路去解决几何问题，这无意地削弱了几何的作用范围，掩盖了几何的一种天然美感。

(8) 追求“形思考、数计算”的几何计算模式。应该以几何学家的思路去考虑问题——宏观而慎密，以代数学家的方式去解决问题——严格而有序。与人的图形认知能力相匹配，在几何的框架下宏观设计，按照代数的方式有序求解。

代数管数，几何管形。数引出数计算，形可否引出形计算？其实，形计算早已有之，在希腊科学中几何学就是占统治地位的：量被解释为长度，两个量之积解释为矩形、面积等。画法几何的尺规作图方法本质上就是一种形计算。因此，计算不应该只是数计算，还应该有形计算。

3 图学中的形计算

图学计算的基础面临新的挑战，图学计算将向着多元化、多学科相融合的方向发展，稳定性将成为图学计算的研究热点与难点。为此需要更优秀的图学计算理论、算法和系统架构，满足图学计算精确性、鲁棒性和可扩展性的需要。探索一种发挥几何直观简洁特点的几何化求解方法，追求形、数结合的新突破。

下面介绍的“形计算”机制[4,16-26]基于下列认知：将思维、几何、代数及计算在几何计算中定位在4个不同的层次：思维是认知与设计层次、几何是表述层次、代数是计算层次、计算是实施层次。基于几何问题几何化的思路，“回归几何”，淡化代数化计算。寻求建立一种“三维思维，二维图解，一维计算”的多维空间融合，追求形-数的顺滑过渡。加强人在计算中的主控地位，更好发挥人的空间逻辑思维。将对数计算的非可读性、几何奇异引起的计算不稳定性等方面有较大的改善。

3.1 形计算的理论基础

解决一个问题首先是要清晰、简单的表述它，如果连表述尚且困难，何来解决问题？

针对图形图像的新需求，为了适应新的计算，一些理论和方法被建立起来去描述新的计算对象。如图论采用图的形式建立关系图，能充分发挥人善于形象思维的优势；数据结构理论将数分成了参数域和指针域以及树结构等。特别是不真正参与运算的指针的引入使常规的计算有了质的变化。在点形成线，线形成面，面构造形体的几何计算中，指针对解决形体的表述，简化复杂的几何算法(例如布尔运算)有很大的作用。这些，实际上是对数制与计算单元的扩充。

(1) 数制。现在用的记数制是位值制，例如十进位值制。用这种方法写出的数字，它的大小不仅和用到的数字符号有关，还和这些符号所在的位置有关。这是一个很美妙的发明。计算机能够用于计算，首先就是解决如何用0/1机制表述十进位值制，冯·诺依曼二进制数制奠定了计算机的计数理论[20]，以及八进制、十六进制和浮点数表示方法使计算机的数字计算得以实现。

对几何计算，Leibniz就认为应该有一种“几何代数”，其接近于几何本身，每个表达式都有明确的几何解释，其元素被称为“几何数”[16]。由几何数处理几何体，实现几何计算的设想本质就是解决几何体的数制问题。形计算机制将采用 Leibniz几何数的名字，引入几何数表征几何的表述。数制问题解决了，形计算就有基础了。

(2) 计算单元。几何代数化已经给出了基本几何元(点、线、面等)的表述，一些基本几何体(锥、柱等)主干表述也已给出，除了它们的范围以外(例如表示圆柱除了方程x2+y2=R2，外加h1≤z≤h2表示范围)。形计算机制将在几何代数化的基础上引入“几何基”的概念。几何基的引入吸取了画法几何“尺规作图”，高等代数线性空间“任一向量可以用它的基底线性表出”以及计算机算法的思想。几何基的原始模型可以作以下抽象化的表述：几何基是几何元操作的抽象表示，一种对几何元的原子操作，也是几何关系的表现，它构建了几何解的基础。由此，对几何问题解的新解读就变成：“几何问题的解可由几何基的序列表述”，它类似于计算结果由一系列的计算单元按照一定的算式表述出来。

3.2 形计算在计算中的地位

当然，不能严格的照搬数计算机制的模式去定义、去理解这个形计算，其更多的是在人的思考层面、解决几何问题的框架层面和算法的设计层面，表述不同维度下的形数转化机制。

图 1展示了形计算(虚框)在整个计算中的地位。提出形计算的背景是图形/图像已成为计算的主要对象与目标，其源头是形,而形的基础是几何。形计算机制是一种基于几何的计算概念与机制，其将几何看做计算单元，以求取几何间的关系作为计算目标。从形的角度去揭示画法几何与几何的共性问题，将其应用于几何计算中。探索以形为核心，将几何、画法几何、代数和计算机等多学科理论与方法的长处融合在一起，达到所谓的“形思考、数实施”，更好发挥人擅长思维与计算机擅长计算各自的特长。

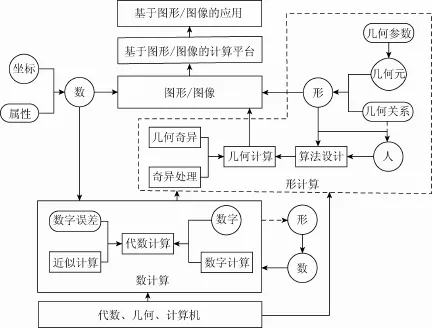
图1 形计算在计算中的地位

3.3 引入几何数

引入几何数(geometric number)，协助表征几何的定义与几何间关系的表示，并辅助整个计算过程。

天地万物，阴阳而已。一个阳爻符号“－”与一个阴爻符号“--”书写了一部易经，“0”与“1”构建了整个计算机体系，物理中电之“正/负”、电路之“开/关”，···，均那阴/阳之分也。几何定义之“左/右(向量)”、“内/外(边界)”、“进/出(交点)”，几何关系之“离/交/切/含”，几何度量之“正/负(面积)”、“逆/顺(角度)”等等何尝不只是阴阳之分？借用了 Leibniz几何数一词。在形计算中引入几何数表示几何的阴/阳两极，它隐含在几何的表示、构造、定位、度量及几何间的关系处理的各个方面。如：

(1) 对基本几何元直线、圆(弧)、面等引入方向(左/右、顺/逆、前/后)；

(2) 对几何的长度、面积、体积等引入正负(正/负)；

(3) 将几何边界分成外边界与内边界(左/右)；

(4) 对两几何间的交点区分“入点/出点(负/正)”；

(5) 若干几何间的连接遵照“皮带轮法则”；

(6) 对描述直线、平面等的系数进行规格化(单位法向量)；

(7) 强调几何在“标准坐标系(计算坐标系)”下描述；等等。

几何数的定义符合自然规律，也符合人的认知体系，其引入将能更好的表述几何的属性，使几何间的关系也更清晰。

几何数在形计算中的作用是多方面的，表2列出了它在几何表示、简化计算、解的选择等方面作用的例子。

3.4 引入几何基

引入几何基(primary geometric basis)作为形计算的基本单元。《红楼梦》只用了4 462个不同汉字，关键是如何组织。几何形体、图形图像无非由点线面构造。几何元素通常有 25种，建立一个通用的定义与求交函数库，最终“字数”也就 C252+25=325个。几何基按一定的关系组合起来就构建了形的构造树，树的遍历就是形的解(图2)。

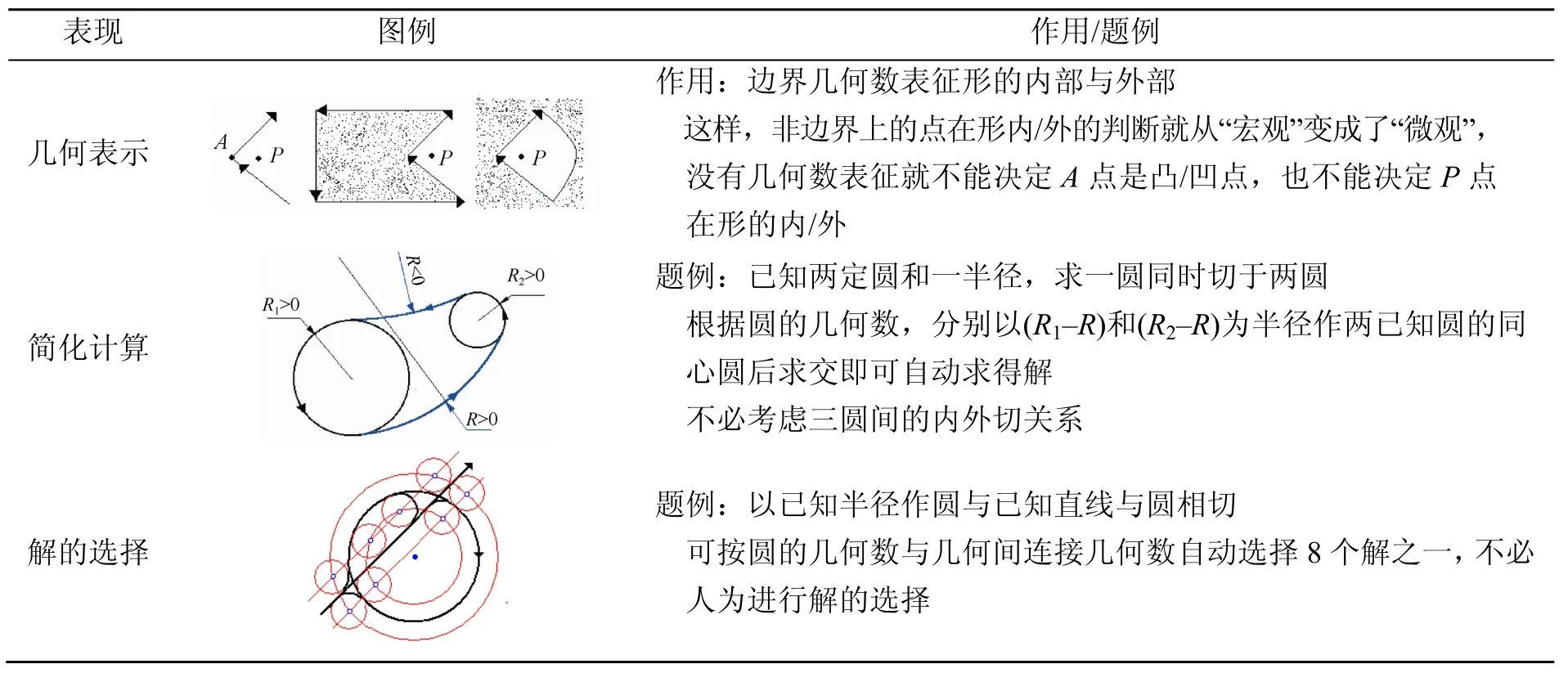
表2 几何数在几何表示、简化计算、解的选择中作用的一些例子

几何基运用公理去诱导几何推理计算，处理几何元之间的几何关系，而非用纯代数计算去解决几何问题。从解的形式来看，几何问题的求解形式表现为几何基的序列，即几何元的操作序列组成问题的解，使计算的每一个步骤都具有几何意义。使几何问题的求解结构化、直观化、简单化。

用一个“求取过平面上3点的圆”例子来阐述用几何基求解平面几何问题的实施过程。(图 2)如果将“作 2点的垂直平分线”的几何基命名为“LPPN()”(表述时只需名字而省略参数)，将“求两直线的交点”的几何基命名为“PLL()”，“CPPP()”表述为 3点所求的圆。用几何基序列表示就是：CPPP()={LPPN，LPPN，PLL}。表3列出了这个求解过程。

图2 3点求圆树结构求解示意图

表3 过平面上3点作圆的几何求解过程与几何基序列表述

这种从几何的角度描述并求解的原理将繁复的代数计算隐藏在几何基中，使算法设计的思考过程变得直观，也更宏观。求取交点的代数实施过程被隐含了。因此，引入几何基是企图淡化(或隐藏)代数表述和代数运算，表现出的是用空间的思维去构建与描述整个求解过程。

3.5 几何变换几何化

形计算中几何变换的重点不是空间几何的平移、旋转等常规变换，而是通过揭示几何代数化的要素为三维形的降维服务。几何代数化的基础是引入坐标系，坐标系是什么？平面上任意两条共点不共线的单位向量或空间任意3条共点不共面的单位向量就构成一个坐标系。同一几何在不同坐标系下有不同的表述，但几何是不变的。因此，对任一几何一定可找到一组最佳向量构建坐标系，在这个坐标系下，几何的表述、求解以及几何间相交关系的求取是最简单的，称为“计算坐标系”。计算坐标系的引入使点、线、圆、面等基本几何，以及三角形、球面、锥面、柱面等基本体素能在它们所谓的“标准坐标系”下解析描述，使几何的表述与相交关系的求取更为简单。空间几何的降维也一般可在正投影下进行，表述简洁，计算复杂度也常会降低。

所谓变换几何化[9-11]其最基本的表述是：平面上任意两条相交(不共线)的单位向量构成一个新坐标系，新旧坐标系间的坐标变换可由两条相交向量在原坐标系下的直线方程系数及齐次项表出。空间任意 3个相交平面的单位法向量构成一个新坐标系，新旧坐标系间的坐标变换齐次矩阵由3个相交平面的规格化方程系数及齐次表出。

变换的几何化表示方法所得到的齐次矩阵统一描述平移、旋转、错切、对称和比例等变换，而且它的矩阵元素可由基本几何(向量、平面)的定义求解系统得到。

3.6 形计算的基本架构

形计算的基本架构如下(图3)：

(1) 对变换实施几何化，尽量使计算在相关几何的“标准坐标系(计算坐标系)”下实施。

(2) 引入几何数，协助表征几何的定义，表述几何间的关系，并辅助整个计算过程。引入几何基，构建基本几何的定义、相交等的基本工具，作为形计算的基本几何单元。

(3) 对三维的形，以解决表示为主，在几何数的协助下，表征几何体的构造关系，以形为纲，在空间层面整体考虑几何问题的求解方案；然后，根据主几何元建立相应的计算坐标系，参考2D/3D对应理论，建立三维形与二维图的映射关系，将空间问题降为平面问题。

(4) 对二维的形和图，以求解为主，主要基于画法几何投影理论和变换几何化机制，解决3D几何体降维以后的几何的求解关系，建立几何问题的构造树。

(5) 在线性空间，则是以代数计算为主，在平面上求得几何基序列解，最后反变换返回到空间问题的最终解。形计算机制强调在几何体整体下的降维，和顺解决(几何)表述空间与(代数)线性计算空间不统一问题，顺势解决几何奇异问题，提升算法的稳定性。

图3 形计算的总体框架与求解机制

3.7 基于几何数的几何奇异处理[20]

几何计算不稳定的主要原因是“几何奇异”(理论层面)和“计算误差”(实施层面)。判定是否几何奇异(未知问题变成已知问题)与处理几何奇异问题(解决一个已知问题)是计算稳定性(共性问题)的两个方面。如何在理论上(整体)解决几何奇异问题一直没有很好解决。

下面阐述如何依据“交点几何数”概念简洁、有效地去解决几何奇异问题。设两向量的交点的几何数取“入点”为“-1”，“出点”为“+1”，那么就有如下重交点与重边交点处理规则。

(1) 重交点取舍规则(图4)：将重交点的几何数累加，若几何数的代数和为0，则取消形成此重点的各交点；否则，合并为一个交点，并以代数和的符号作为其几何数。

(2) 重边交点的取舍规则(图5)：如果在同一向量上有连续两个交点的几何数相同，则若几何数均为+1，删除后一个交点；若几何数均为-1，删除前一个交点。

两个规则只是对交点几何数的简单运算，但从理论层面上解决了已知几何关系奇异问题。

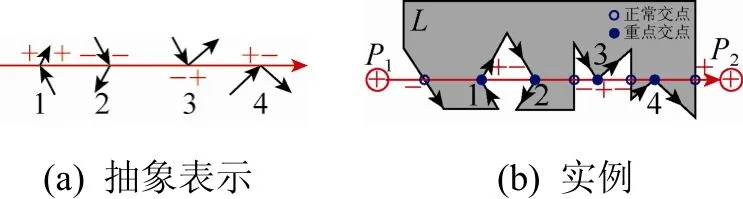
图4 重交点的取舍

图5 重边交点的选择

图 6给出了用几何数解决各类奇异问题的方案，图7给出解决计算稳定性的总体方案。

图6 引入几何数解决几何奇异问题的实施方案

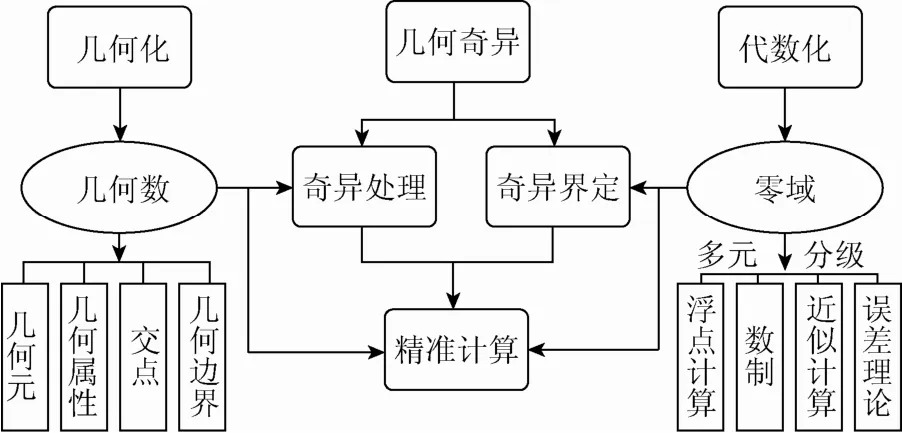
图7 形计算中解决计算稳定性的总体方案

3.8 形计算若干例子

下面给出用形计算机制处理几何计算的一些实施例子[9-11,21-26]。

3.8.1 降维的二维矩形窗口裁剪[9]

Liner2D算法将二维裁剪降维化成二次一维裁剪，二次一维裁剪分x方向与y方向独立进行，合并两次裁剪的结果就得到最后的裁剪结果。

设被裁剪线P0P1是用参数形式P=P0+(P1-P1)t表示的，如图8所示。P0P1在裁剪窗口中的可见部分为：

P0P1∩LR∩BT，即[0,1]∩[t1,t2]∩[t3,t4]。

图8 基于降维的二维裁剪

对基于线性裁剪的Liner2D算法与国际上认可的 3种裁剪算法 CohenSutherland、CyrusBeck、LiangBarsky进行了测试与对比，测试样品采用6+61条线段，其中含对角线的菱形6条线为各种方位的常规线段，61条线遍历了被裁剪线与矩形窗口的各种位置(含奇异位置，图9)。

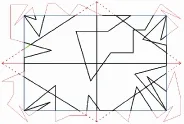
图9 4种矩形裁剪的测试样例与结果

正确性，4种算法都能正确的对这些线段作出裁剪。

计算效率的测试分成两种：①是各种布局的线段的测试，即对所有67条线重复进行50万次裁剪；

测试结果见表 4，4种方法所花的计算时间在同一个数量级上，稍有区别。

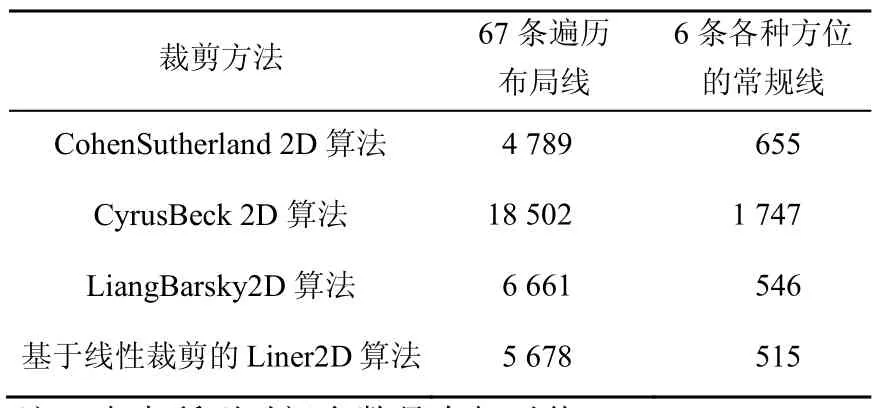
表4 4种矩形窗口裁剪的计算效率参考表

3.8.2 基于投影降维的视锥体裁剪

视锥体裁剪是计算机图形学的一个重要而基础的算法，下面的算法利用画法几何的投影理论，将3D计算降为2D计算。

以视锥体的底平面及两个对称平面作为坐标平面构成计算坐标系，以视锥体下底中心到上底中心的向量作为 z轴，建立视锥体的计算坐标系(图10)，利用画法几何理论建立V/W投影体系，在这个计算坐标系下，视锥体在V面上的投影Tv与在W面上的投影Tw均为等腰梯形(图11)。空间直线投影在V面与W面上分两次裁剪，它们的交集即为三维裁剪结果。

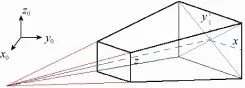
图10 视锥体计算坐标系

图11 视锥体二次裁剪原理图

比较了3种算法，“Liang-Barsky视锥体裁剪方法”、“线面直接求交”算法和“基于投影降维的视锥体裁剪”算法。设计了包含与视锥体顶点、边界线和边界面处于奇异状态的78组被裁剪线段样本，在经过预处理之后的标准坐标系下，对这78个样本重复10万次裁剪的计算，计算时间的参考比例为：

L-B：线面求交：投影降维=4243：4228：4212说明3种算法的计算效率在同一数量级上。

需要强调的是，上面两个窗口裁剪和视锥体裁剪算法与经典算法作了比较，似乎在时间上并不占有优势，但这是形计算机制下的规则算法与专门研究的个体化算法的比较。

3.8.3 基于几何数的几何形体布尔运算

文献[21]叙述了一种基于几何数的十分简单的二维布尔运算算法。边界的几何数使图形边界划分为有内边界与外边界，交点的几何数决定了交点是入点还是出点，算法原理十分简单。

二维图形布尔算法(图12)：从某一个交点出发，对并(交、差)运算，若交点几何数为负(正)，则转向另一环(顶点则按原走向搜索下去)，直至回到出发时的首交点，就得到一个新边界(环)。一旦所有交点均被遍历，算法结束(这里省略了重边界的处理)。

在此，交点的几何数能够根据运算的性质协助决定环的走向，新边界的内外性质在求解过程中同时被确定，也避免了从顶点出发需要进行繁琐的包容性测试，计算工作量较少。运算中的几何奇异问题也可由交点的几何数简单的予以解决。

图12展示了对两个图形A与B求并集的形运算过程，分别从交点10和交点13出发得到A与B并集的两条边界(图12(b)，圆圈里的数字为交点，方框里的数字为顶点)。

这个方法也可以方便的扩展到三维形体的布尔运算(图13)。

图12 对2个图形A与B求并集的形运算

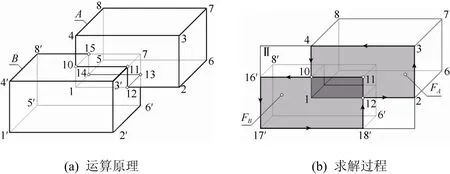
图13 三维布尔运算的原理

3.8.4 空间几何的相交计算[9,21-26]

空间问题的形计算尽量采用降维计算，通常会利用画法几何的投影与2D/3D对应理论。根据主几何元建立相应的计算坐标系，参考 2D/3D对应理论，在三维整体概念下建立空间几何与平面图形间的映射关系，得到三维形的二维图表示，将空间问题降为平面问题。在平面上求得几何基序列解，最后反变换返回到空间问题的最终解(这也构成一个三维几何基)。

空间两几何的求交算法可简单表述如下(空间直线与球面求交算法为例)：

步骤 1. 根据参与运算几何元的性质，构造计算坐标系(以球心为原点，直线方向为x轴方向构建计算坐标系。参阅图14，下同)，建立V/W/H绝对投影体系。将参与计算的两个几何元的参数(点的坐标，球中心与直线的两端点)变换到计算坐标系下。

步骤2. 应用2D/3D对应理论建立空间几何元降维前后的计算关系，形成投影面上的计算方案(在两个投影面上分别求直线投影与圆①与圆②的交点)。在两投影平面各自构造几何基序列，分别得到两几何元交点在两投影面上的坐标参数，并将其合成为三维交点参数。

步骤 3. 如果有交点，将得到的交点参数逆变换回原始坐标系。

算法包括预处理(步骤1，构建计算坐标系并作正向变换)、实施(步骤 2，在新坐标系下的坐标平面上求取交点，这是用几何基的序列表述的)和后处理(步骤3，将交点坐标逆变换) 3步。其中，求交过程在二维平面上进行，例中用了两次“直线与圆求交”几何基。

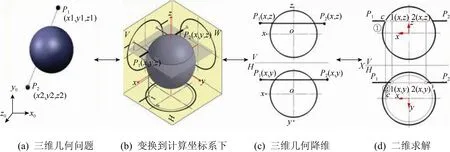
图14 用形计算求取空间直线与球面交点的实施过程

3.8.5 两空间三角形的位置关系[9,26]

空间两三角形相互关系判定与计算是有限元分析、碰撞检测中的基础算法。

设两个三角形A与B所在的平面分别为ΠA，ΠB，两平面的交线为L，A与ΠB的交线段为LA，B与ΠA的交线段为LB，则LA与LB必定在L上，若LA与LB有重叠部分，则两三角形相交(图15(a))，否则就相离(图15(b))。直接空间判别比较复杂。

下面的算法通过降维的办法简化两三角形的关系，并解决几何奇异问题(图16)。

图15 两三角形空间求交的基本原理

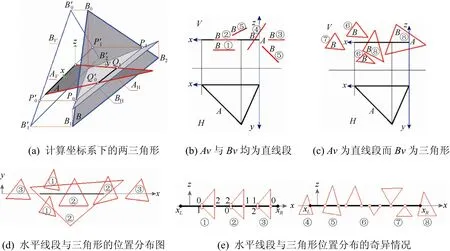
图16 经降维后的空间两三角形关系简化、奇异状态清晰

先建立一个计算坐标系，使其中一个三角形在该计算坐标系的一个坐标平面上(图16(a))。这样，该三角形在计算坐标系的V投影坐标平面上的投影为直线段和直线段(图16(b)，在W面上的投影也是直线段)，在 H投影平面上的投影保持原始三角形(图16(b), (c))。经过投影降维后，两个三角形的关系将分别在两个坐标平面上处理，转变成“线段-线段”、“线段-三角形”的关系(图 16(b), (d))，相互关系简化，奇异状态也变得更清晰。

4 结 论

研究图的科学应统一被称为“图学”，图学研究形和图的表示、表现以及互相关系，其基本内容应该包含以下几个方面：造型理论与方法、由形→图的理论与方法、图的处理理论与方法、由图→形的理论与方法以及图的传输理论与方法等。

图源于形，几何构造了形与图。因此图学的核心是形，本质是几何，图学计算的主要工作是几何计算，理论基础是几何学。只有基于计算与几何两个最核心的要素，才能清晰图学与几何的关系。即图学研究的目标是图、核心是形、本质是几何，最根本的理论基础是几何学。这些理论、方法和技术会借助于其他学科或是学科交叉。

计算是一切的基础，计算的基础是数学。数学上主要有两种推理：符号推理与直观推理，前者源于计数制，后者源于图形制。继数之后，形作为数学的第二个主要概念被引入，形能充分发挥人的空间思维特长。

通过对图和形内涵的分析，论述了处理图形计算中的三个核心关系：几何关系、形数关系和维度关系。指出求取新的几何关系是图学计算的目标与主要工作；处理好维度关系，从而解决思维空间与计算空间、表述空间与显示空间维度不统一问题是图学计算的关键；几何代数化引起三维几何形表述与线性代数计算之间形数关系出现跳跃，解决形数关系的顺滑过渡是图学计算的纲。

介绍了一种发挥几何直观简洁特点的几何化求解方法，即“从定性、直观的角度去思考，以定量、有序的方式去求解”的思路，寻求“三维思维，二维图解，一维计算”多维空间融合的求解机制，追求形-数顺滑过渡的新突破。算例表明，形计算能够弥补常规数计算的不足，对数计算的非可读性，奇异引起的不稳定性会有较大的改善。这种“形思考”、“数计算”的几何计算新模式将能更好地发挥人在计算机中的主控地位。

(东华大学于海燕副教授，上海交通大学蔡鸿明、柳伟副教授，大连理工大学王子茹教授参与了讨论，特致谢意。)

[1] 中国图学学会. 2012-2013图学学科发展报告[R]. 北京:中国科学技术出版社, 2014.

[2] 何援军, 童秉枢, 丁宇明, 等. 图与图学[J]. 图学学报, 2013, 34(4): 1-10.

[3] 于海燕, 蔡鸿明, 何援军. 图学计算基础[J]. 图学学报, 2013, 34(6): 1-6.

[4] 何援军. 一种基于几何的形计算机制[J]. 图学学报, 2015, 36(3): 1-10.

[5] 何援军, 王子茹. 谈谈图学教材[J]. 图学学报, 2015, 36(6): 819-827.

[6] 何援军. 计算机图形学[M]. 2版. 北京: 机械工业出版社, 2009: 1-9.

[7] Miller J R. Vector geometry for computer graphics [J]. IEEE Computer Graphics and Applications, 1999, 19(3): 66-73.

[8] Duckworth T, Roberts D J. Accelerated polyhedral visual hulls using opencl [C]//IEEE Virtual Reality Conference. New York: IEEE Press, 2011: 203-204.

[9] 何援军. 几何计算[M]. 北京: 高等教育出版社, 2013: 1-19.

[10] 何援军. 几何计算及其理论研究[J]. 上海交通大学学报, 2010, 44(3): 513-517.

[11] 何援军. 对几何计算的一些思考[J]. 上海交通大学学报, 2012, 46(2): 18-22.

[12] 吴文俊. 初等几何判定问题与机械化问题[J]. 中国科学, 1977, (7): 507.

[13] 吴文俊. 数学机械化——回顾与展望[J]. 系统科学与数学, 2008, 28(8): 898-904.

[14] Ericson C. Triangle-triangle teste, plus the art of benchmarking [EB/OL]. [2016-04-15]. http:// realtimecollisiondetection.net/blog/?p=29.2007,9.12,File d under Robustness, from hell, Code.

[15] Atiyah M. 二十世纪的数学[J]. 数学译林, 2002, (1): 1-24.

[16] 将几何代数化的数学家——笛卡儿[EB/OL]. [2016-04-15]. http://bbs.matwav.com/archiver/? tid-137115.html.

[17] 刘克明, 杨叔子. 画法几何学的历史及其现代意义——纪念蒙日画法几何学公开发表 200周年[J]. 数学的实践与认识, 1998, 28(3): 281-288.

[18] 霍 金. 时间简史——从大爆炸到黑洞[M]. 许明贤,吴忠超, 译. 长春: 北方妇女儿童出版社, 2003: 1-5.

[19] 张景中. 几何问题的机器求解[J]. 科学, 2001, (2): 20-23.

[20] 百度百科. 冯诺依曼体系结构[EB/OL]. [2016-04-15]. http://baike. baidu.com/view/7719.htm.

[21] 章 义, 于海燕, 何援军. 二维布尔运算[J]. 上海交通大学学报, 2010, (11): 1486-1490.

[22] Yu H Y, He Y J. 3D geometrical intersection based on dimension reduction [C]//The 15th International Conference on Geometry and Graphics (ICGG 2012 Montréal, Canada), 2012: 8.

[23] Yu H Y, He Y J. Geometric computing based on computerized descriptive geometry [J]. Computer Aided Drafting, Design and Manufacturing (CADDM), 2011, 21(2): 55-61.

[24] Yu H Y, He Y J, Wang Y X. Evaluation on triangle-triangle intersection tests algorithms [C]//The 16th International Conference on Geometry and Graphics (ICGG 2014, Innsbruck, Austria), 2014: 8.

[25] Lin W, Yu H Y, He Y J. A preliminary framework for geometric basis computing pattern [C]//Proceedings of the 2010 IEEE International Conference on Progress in Informatics and Computing. New York: IEEE Press, 2010: 710-713.

[26] 于海燕, 何援军. 空间两三角形的相交问题[J]. 图学学报, 2013, 34(4): 54-62.

Graphics and Geometry

He Yuanjun
(Department of Computer Science & Engineering, Shanghai Jiao Tong University, Shanghai 200240, China)

The relationships between graphics and geometry are discussed in this paper. From the view that shape is the source of the graph, the drawing/image are fundamentally constructed by geometric elements, thus the process of generation, representation, processing and propagation of drawing/image could be regarded as some operations of definition, transformation and interrelation of geometric elements. Therefore, it can be concluded that geometry is the basis of graphics and its theory, and meanwhile geometric computing is also the basis of graphics computing. Then, based on the analysis of graphics and its computing fundamentally, the essence, contradiction and key technologies of graphics computing are presented. The respective roles and advantages/disadvantages of algebra and geometry, emphasizing the leading status of human in the design of algorithms are also discussed. Moreover, the generation of a drawing or a model depends more on the relations between their elements than the elements themselves. Since the drawing/images have become the major objects and representation in graphics computing, a geometry-based shape calculation mechanism is introduced to fix the shortage of normal numerical calculation mechanism, so as to pursuit a new mode of geometric computing as thinking by shape while computing by number.

graphics; geometry; geometric computing; numerical computing; shape computing

TP 391

10.11996/JG.j.2095-302X.2016060741

A

2095-302X(2016)06-0741-13

2016-05-03；定稿日期：2016-06-19

何援军(1945-)，男，浙江诸暨人，教授，博士生导师。主要研究方向为CAD/CG、几何计算。E-mail：yjhe@sjtu.edu.cn