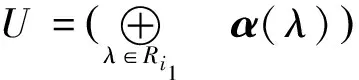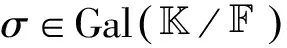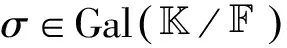Galois理论在高等代数中的若干应用

2017-01-18谢启鸿

大学数学 2016年6期

关键词：角化特征向量代数

谢启鸿

(复旦大学数学科学学院，上海200433)

Galois理论在高等代数中的若干应用

谢启鸿

(复旦大学数学科学学院，上海200433)

给出了Galois理论在高等代数若干问题中的应用.

分裂域; Galois扩张; 特征多项式; 特征值; 特征向量; Jordan-Chevalley分解

1 引言

首先, 我们阐述域论中的一些概念和结论 (参考教材[1]).设f(x)是域上的多项式, f(x)在上的分裂域是的一个扩域, 使得f(x)在上可分解为一次多项式的乘积, 并且在同构意义下,是满足上述性质的的最小扩域.具体的, 若取的一个代数闭包, 并设f(x)在中的全体根为λ1,λ2,…,λn, 则=(λ1,λ2,…,λn).类似地, 还可定义上一族多项式的分裂域, 这样的扩域称为上的正规扩张.对于正规扩张, 有如下的同构扩张定理.

定理1设是上的正规扩张, λ∈在上的极小多项式为m(x), 则对m(x)的任一根μ, 存在一个保持中元素不动的的自同构使得σ(λ)=μ.

定理2设/是有限Galois扩张,M={|⊇⊇}为/的中间域全体,S={G|G≤Gal(/)}为的子群全体, 定义

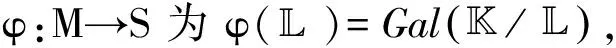
ψ:S→M为ψ(G)=InvG={λ∈|σ(λ)=λ,∀σ∈G}(G的不变子域),

则φ,ψ给出了M,S之间的反序一一对应.特别地, 若λ∈满足σ(λ)=λ对任意的都成立, 则λ∈.

为了利用Galois理论处理高等代数问题, 需要将Galois群对域的作用延拓到列向量、矩阵和多项式上.设/是一个有限Galois扩张则对任一列向量

α=(a1,a2,…,an)T∈n, A=(aij)∈Mn([x],

定义

σ(α)=(σ(a1),σ(a2),…,σ(an))T∈n,

σ(A)=(σ(aij))∈Mn(),

Inv(V)={α∈V|σ(α)=α,∀σ∈Gal(/)},

α=c1e1+c2e2+…+crer,

其中c1,c2,…,cr∈, 从而

σ(α)=σ(c1)e1+σ(c2)e2+…+σ(cr)er.

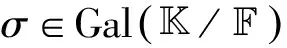
Inv(U⊕U⊕…⊕U)=U1⊕U2⊕…⊕Uk.

先来看一道可对角化矩阵的典型例题.

例1设A∈Mn()的特征值λ1,λ2,…,λn都在中, 并且这n个特征值互不相同, 再设对应的特征向量为α1,α2,…,αn∈n, 证明:n的任一A-不变子空间U必为如下形式:

U=αi1⊕αi2⊕…⊕αir,

其中{i1,i2,…,ir}是{1,2,…,n}的子集 (注: 空集∅对应于零子空间).

证由假设可知A在上可对角化, α1,α2,…,αn是A的n个线性无关的特征向量, 并且

n=α1⊕α2⊕…⊕αn.

不妨设U≠0, 容易验证A|U的特征多项式是f(λ)的因式, 故可设A|U的特征值为λi1,λi2,…,λir, 其中{i1,i2,…,ir}是{1,2,…,n}的子集.由于A|U的特征值互不相同, 故A|U可对角化, 又所有的特征子空间都是形如αij的一维子空间, 所以

U=αi1⊕αi2⊕…⊕αir.

通过例1的证明和结论我们知道, 若A的特征值互不相同, 则任一A-不变子空间U由A|U的全体特征值唯一确定.下面的例题利用了例1的结论, 是Galois理论在高等代数中最典型的应用之一.

例2设A∈Mn()的特征多项式为f(λ), 证明：n只有平凡的A-不变子空间的充分必要条件是f(λ)是上的不可约多项式.

证先证充分性.设f(λ)是上的不可约多项式, 从而f(λ)在其分裂域上无重根, 不妨设为λ1,λ2,…,λn.设U是n的非零A-不变子空间, 只要证明U=n即可.任取U的一组基{e1,e2,…,er}, 由Aei∈U(1≤i≤r)容易验证U是n的A-不变子空间.取A|U的任一特征值, 不妨设为λ1, 对应的特征向量为α1∈U, 即

α1=c1e1+c2e2+…+crer,

其中c1,c2,…,cr∈不全为零.由定理1可知, 存在自同构使得

σi(λ1)=λi(1≤i≤n),

在等式Aα1=λ1α1两边同时作用σi可得Aσi(α1)=λiσi(α1).注意到

σi(α1)=σi(c1)e1+σi(c2)e2+…+σi(cr)er∈U

仍为非零列向量, 故λi(1≤i≤n)都是A|U的特征值.由例1可知U=n, 特别地,

U=Inv(U)=Inv(n)=n.

g(A)h(A)=f(A)=O.

因此g(A),h(A)中至少有一个是奇异阵, 不妨设为g(A), 于是存在非零列向量α∈n, 使得g(A)α=0.设degg(λ)=m, 令U=L(α,Aα,…,Am-1α), 则dimU≤m

事实上, 例2也可以利用循环子空间理论来进行证明 (参考 [5] 的命题1).下面的例3是复旦大学数学科学学院2015-2016学年第一学期高等代数I期末考试的压轴题, 它的标准解答是利用循环子空间理论和中国剩余定理来进行证明的, 不过我们可以将例2的充分性证明进行推广, 并利用Galois理论给出新的证明.注意到例3也是例1的一个推广.

例3设A∈Mn()的特征多项式

f(λ)=f1(λ)f2(λ)…fk(λ),

其中fi(λ) (1≤i≤k)是上互异的首一不可约多项式.设Vi=Kerfi(A) (1≤i≤k)为n的子空间, 证明:n的任一A-不变子空间U必为如下形式

U=Vi1⊕Vi2⊕…⊕Vir,

其中{i1,i2,…,ir}是{1,2,…,k}的子集 (注: 空集∅对应于零子空间).

证设f(λ)的分裂域为, 则容易验证f(λ)在中无重根.为方便起见, 记fi(λ)的根的集合为Ri(1≤i≤k),用α(λ)表示特征值λ∈Ri对应的特征向量.由[3]的例7.21可知,

n=V1⊕V2⊕…⊕Vk,

并且A|Vi的特征多项式为fi(λ).因为fi(λ)在上无重根, 故A|Vi在上可对角化, 并且Vα(λ).设U是n的非零A-不变子空间, 则U是n的非零A-不变子空间.若λ∈Ri是A|U的一个特征值, 则由类似于例2充分性的证明可知, Ri中的任意元素都是A|U的特征值, 再由例1可知

其中{i1,i2,…,ir}是{1,2,…,k}的子集.因此U=Vi1⊕Vi2⊕…⊕Vir, 于是有

U=Inv(U)=Inv(Vi1⊕Vi2⊕…⊕Vir)=Vi1⊕Vi2⊕…⊕Vir.

为了得到下一个应用, 先来证明一个有趣的命题.

例4设A,B∈Mn(), A,B的特征值都在中, 并且r(AB-BA)≤1, 证明: 存在非异阵P∈Mn(), 使得P-1AP和P-1BP同时为上三角阵.

证对阶数n进行归纳, 当n=1时, 结论显然成立.设阶数小于n时, 结论成立, 现证n阶的情形.若AB=BA, 则由 [3] 的例6.50可知结论成立; 若A=O, 则结论显然成立; 又若A非异, 则任取A的特征值λ1∈, 用A-λ1In代替A进行讨论.因此可设r(AB-BA)=1, 并且KerA和ImA都是n的非平凡子空间.我们先证明: A,B有公共的非平凡不变子空间.若B(KerA)⊆KerA, 则KerA就是A,B公共的非平凡不变子空间.下设B(KerA)⊄KerA, 即存在α∈KerA, 使得Bα∉KerA.注意到

(AB-BA)α=A(Bα)-B(Aα)=A(Bα)≠0,

又r(AB-BA)=1, 故Im(AB-BA)=A(Bα)⊆ImA.对任一Aγ∈ImA, 有

B(Aγ)=A(Bγ)-(AB-BA)γ∈ImA,

于是ImA也是B的不变子空间.

设U是A,B公共的非平凡不变子空间, 选取U的一组基并扩张为n的一组基, 则A,B在这组基下的表示矩阵都是分块上三角阵, 即存在非异阵Q∈Mn(), 使得

由r(AB-BA)=1可得r(AiBi-BiAi)≤1, 再分别对Ai,Bi(i=1,2)运用归纳假设即得结论.

下面的例5可以利用线性方程组的求解理论和互素多项式的应用进行纯代数的证明; 也可以利用循环子空间的理论进行纯几何的证明 (参考 [5] 的例2), 在上述两种方法中, 特征多项式f(λ)在上的不可约性和tr(AB-BA)=0都是证明的关键点.接下来我们将利用Galois理论给出例5的第三种证明, 注意到其证明过程没有用到矩阵迹的技巧.

例5设A,B∈Mn(), 并且A的特征多项式f(λ)是上的不可约多项式, 证明: r(AB-BA)≠1.

证用反证法证明结论, 设r(AB-BA)=1.取为A,B的特征多项式的分裂域, 则由例4 可知, 存在非异阵P∈Mn(), 使得P-1AP和P-1BP同时为上三角阵.设P的第一列为α1∈n, 则α1≠0是A,B公共的特征向量, 即有

Aα1=λ1α1，Bα1=μ1α1,

(1)

其中λ1,μ1分别为A,B的特征值.由于f(λ)在上不可约, 故A的n个特征值λ1,λ2,…,λn∈互不相同, 对应的特征向量必线性无关.由定理1可知, 存在使得σi(λ1)=λi(1≤i≤n).将σi作用在 (1) 式上可得

Aσi(α1)=λiσi(α1),Bσi(α1)σi(μ1)，σi(α1), 1≤i≤n.

(2)

由于σi(α1)≠0, 故它是矩阵A关于特征值λi的特征向量, 也是矩阵B关于特征值σi(μ1)的特征向量, 从而σ1(α1),σ2(α1),…,σn(α1)必线性无关.令

Q=(σ1(α1),σ2(α1),…,σn(α1))∈Mn(),

则Q是非异阵, 使得

Q-1AQ=diag{λ1,λ2,…,λn},Q-1BQ=diag{σ1(μ1),σ2(μ1),…,σn(μ1)},

于是AB=BA, 这与r(AB-BA)=1矛盾.

作为Galois理论的应用, 最后我们将证明一般域上的Jordan-Chevalley分解定理.

例6设A∈Mn(), 证明: 存在分解A=B+C, 其中B,C∈Mn()且满足

(i)B在其特征多项式的分裂域上可对角化;

(ii)C幂零, 即存在正整数m, 使得Cm=O;

(iii)BC=CB;

(iv) 存在多项式g(x)∈[x], 使得B=g(A),并且满足条件 (i)—(iii) 的上述分解必唯一.

证设为A的特征多项式的分裂域, 完全类似于复矩阵的Jordan-Chevalley分解定理的证明 (参考 [2] 的定理7.7.3), 可以得到A在上的Jordan-Chevalley分解, 即存在分解A=B+C, 其中B,C∈Mn()且满足:

(i)B在上可对角化;

(ii)C幂零;

(iii)BC=CB;

(iv) 存在多项式h(x)∈[x], 使得B=h(A),并且满足条件 (i)—(iii) 的上述分解必唯一.对任一可得A的另一分解

A=σ(B)+σ(C),

其中σ(B)在上仍可对角化,σ(C)仍幂零, 并且

σ(B)σ(C)=σ(C)σ(B).

h(x)=h1(x)+k2h2(x)+…+kdhd(x),

其中hi(x)∈[x].再由B=h(A)可得B=h1(A), 取g(x)=h1(x)即得结论.

一般来说, 大基域上的对象往往更容易被刻画或分类, 因此小基域上的对象可以提升到大基域上进行研究.Galois群关于基域的对称作用也传递给了研究对象及其性质, 因此可以将这些大基域上的性质下降到小基域上, 从而得到相应的刻画或分类.换言之, Galois理论提供了一种下降理论 (Descent Theory), 这种理论对于现代代数学、代数几何和代数数论等分支的研究起到了重要的作用.

一般域上的高等代数问题, 可以利用线性变换理论和一般域上的相似标准形理论等加以研究; 也可以利用高等代数中若干概念在基域扩张下的不变性把问题提升到大基域上进行研究 (参考 [4]); 而本文列举的四个例题则告诉我们, 还可以利用Galois理论的下降功能来研究一般域上的高等代数问题.这些方法和技巧不仅将专业课近世代数和基础课高等代数紧密地联系在一起, 而且利用像Galois理论这样优美的理论工具来解决问题, 充分展现了代数学的神奇魅力.

[1] 姚慕生.抽象代数学[M].2版.上海: 复旦大学出版社, 2005.

[2] 姚慕生, 吴泉水, 谢启鸿.高等代数学[M].3版.上海: 复旦大学出版社, 2014.

[3] 姚慕生, 谢启鸿.高等代数，大学数学学习方法指导丛书[M].3版.上海: 复旦大学出版社, 2015.

[4] 谢启鸿.高等代数中若干概念在基域扩张下的不变性[J].大学数学, 2015, 31(6): 50-55.

[5] 谢启鸿.循环子空间的若干应用[J].大学数学, 2016, 32(1): 1-6.

Some Applications of Galois Theory in Advanced Algebra

XIEQi-hong

(School of Mathematical Sciences, Fudan University, Shanghai 200433, China)

We give some applications of Galois Theory to certain problems in Advanced Algebra.

splitting field; galois extension; characteristic polynomial; eigenvalue; eigenvector; Jordan-Chevalley decomposition

2016-05-09； [修改日期] 2016-08-20

国家自然科学基金(11422101)