基于GNSS浮标和验潮资料的HY-2A卫星高度计绝对定标

杨磊，周兴华*，王朝阳,2，梁冠辉，唐秋华，周东旭,2，雷宁,2，杨龙，穆博

(1.国家海洋局第一海洋研究所，山东 青岛 266061；2.山东科技大学 测绘科学与工程学院，山东 青岛 266590；3.国家卫星海洋应用中心 定标检验部，北京 100081)



基于GNSS浮标和验潮资料的HY-2A卫星高度计绝对定标

杨磊1，周兴华1*，王朝阳1,2，梁冠辉1，唐秋华1，周东旭1,2，雷宁1,2，杨龙1，穆博3

(1.国家海洋局第一海洋研究所，山东 青岛 266061；2.山东科技大学 测绘科学与工程学院，山东 青岛 266590；3.国家卫星海洋应用中心 定标检验部，北京 100081)

为探测我国HY-2A卫星高度计海面高测量绝对偏差及其在轨运行状态，本文利用GNSS浮标星下点同步测量和验潮资料海面高传递方法在山东千里岩和珠海担杆岛海域开展定标研究。为验证GNSS浮标定标方法的准确性，还对国外卫星Jason-2和Saral进行了定标实验。实验表明GNSS浮标绝对海面高测量精度达2 cm，对Jason-2和Saral高度计多个周期定标得到的海面高偏差均值分别为5.7 cm和-2.3 cm，与国际专门定标场的结果符合较好。2014年9月和2015年5月HY-2A卫星高度计浮标定标结果分别是-65 cm和-91 cm，因两次结果差异显著，故又利用千里岩验潮站资料对HY-2A卫星高度计第56至73周期进行了定标分析，结果证明HY-2A卫星海面高存在约-51 cm/a的漂移，置信度为95%的回归分析表明浮标和验潮定标结果符合。本文研究结果表明在我国尚无专门定标场的情况下，可利用GNSS浮标对我国高度计实施灵活、精准的在轨绝对定标，在有高度计轨迹经过验潮站的情况下可使用验潮资料结合精密大地水准面模型进行绝对定标。

GNSS浮标；绝对定标；HY-2A；Saral/AltiKa；Jason-2

1 引言

精确测定全球海平面变化对于研究海洋对全球气候变化的影响具有重要意义，随着卫星测高技术的发展，卫星海面高测量的精度已达到2～3 cm[1—2]，已成为全球海平面监测的重要的手段。2011年我国发射了首颗HY-2A卫星高度计，并计划发射后续的系列高度计卫星，这对于提升我国的海洋监测能力具有重要意义[3—4]。除了HY-2A卫星，目前主要的在轨卫星高度计还有Jason-2和 2013年印度法国合作的Saral/AltiKa高度计[5]，另外于2016年1月17日Jason-2的后续星Jason-3也已成功发射并在轨运行。多颗卫星高度计同步观测可显著提高海面高时空分辨率，对研究中小尺度的全球和局部海洋变化具有重要的意义[6-7]。然而各高度计可能存在不同的系统偏差，同一颗高度计也可能出现因仪器老化带来的漂移现象[8]，因此为了保证不同测高卫星数据的长期一致性和可靠性，通常在卫星运行期间需要在专门的海上定标场进行在轨绝对海面高(SSH)定标，以确定其SSH观测的系统性偏差，并通过改正引起偏差的误差源来提高数据的观测精度和质量，实现不同卫星之间的数据融合和精密衔接[8]。

国外卫星高度计(如Jason-2&3和Saral/AltiKa等)通过国际专门定标场获取了海面高绝对偏差，对于了解卫星在轨工作状态以及数据改进起到积极作用，这些定标场主要位于美国Harvest石油平台[9—11]、澳大利亚Bass海峡[12—14]、法国Corsica岛[7,15—16]，以及希腊Crete岛[17—18]，多数定标场已经跟随不同的卫星任务持续运行了数十年。目前我国公开了HY-2A卫星高度计IGDR数据，但国内外对其开展的绝对定标研究仍然不足，对HY-2A 数据的推广应用和误差改正都有一定的限制。由于我国尚未建立专门的高度计定标场，因此通过国际合作，希腊Crete岛定标场给出了对HY-2A 第54至62周期SGDR的定标结果为(-27±3)cm[18]，然而由于定标时间长度较短，该结果并未探测到Wan等利用有源定标器在陆地发现的HY-2A USO漂移现象[19]。此外彭海龙等利用全球验潮网络对早期的HY-2A IGDR第1至30周期数据进行了相对定标分析[20]，并对HY-2A 第44周期的IGDR数据与Jason-2同期数据进行了差异的统计分析[21]，然而研究表明HY-2A第51周期之前的数据可靠性较差[18,22]，且其研究属于星间交叉分析，故仍未确定HY-2A的绝对偏差结果以及漂移现象。

研究表明在无专门定标场的情况下可利用GNSS浮标开展卫星标定研究[23-24]，该方法是将GNSS浮标直接布放到卫星星下点进行同步海面高观测，和传统的验潮站定标方式比较具有灵活、经济的特点，并可减小大地水准面梯度误差的影响，Harvest平台、Bass海峡和Corsica定标场均使用过GNSS浮标定标[25—27]。国内关于高精度海面测高的GNSS浮标研究依然较少[28]，其中陈春涛等利用其研制的浮标开展了高度计定标试验，但浮标测高偏差有7.40 cm[29—30]。另一种无定标场情况下的定标方法是利用卫星轨迹附近的验潮资料进行定标[31]，主要是利用GPS测量和水准测量对验潮数据的参考基准面进行统一，对验潮站的地理位置和大地水准面精度有特定要求。故针对我国HY-2A IGDR数据绝对定标的问题，本文对HY-2A开展了多期的GNSS浮标的星下点同步观测，为验证HY-2A浮标定标的精度，还对已知绝对偏差的Jason-2和Saral高度计进行定标试验。另外由于浮标测量试验获得的HY-2A定标数据较少，因此在千里岩海洋站开展了水准连测，统一潮位基准面，利用验潮资料对HY-2A第56周期至73周期的历史观测数据进行了定标分析。

2 定标海域

千里岩附近的卫星轨迹分布情况以及GNSS浮标布放点如图1a所示，经过该海域的卫星轨迹有Jason-2的第153轨迹、Saral的第735轨迹和HY-2A的第147轨迹，均为上升轨迹，即海面高观测时间序列与纬度增大方向对应，卫星测高数据质量受陆地影响小。其中Jason-2和Saral卫星轨迹距离千里岩岛的最近距离约2 km，HY-2A轨迹距离千里岩最近约为20 km，因此千里岩定标场具有一岛监控多星的特点。另外千里岩远离大陆，星载微波辐射计不受陆地影响，对高度计距离测量提供的大气湿延迟改正也相对准确。通过分析Jason-2和Saral卫星高度计的SGDR波形数据发现该岛对雷达波形数据无影响，符合开阔海域的波形特征，因此千里岩在空间位置上是前述系列高度计的一个理想定标地点。另一处定标实验地点位于香港南侧的担杆岛，HY-2A的第203轨迹从此经过，同样该轨迹为升轨。

在2014年7月至10月期间选择了卫星集中过境的3次时间窗口，共进行了7次有效定标实验，图1a中圆点表示GNSS浮标布放在Jason-2和Saral卫星轨迹交叉点，HY-2A的定标点则选择了离岛最近点。2015年5月在珠海担杆岛海域开展了一次HY-2A的定标试验，GNSS浮标为图1b中黄点所示，基站位于图中五角星表示的担杆尾。另外由于HY-2A浮标定标次数偏少，本文还利用千里岩验潮资料对数据质量较好的HY-2A 第56周期至73周期进行定标分析。

3 现场测量与数据处理

3.1 浮标测量方案设计

用于本次实验的浮标设计吸收了波浪骑士浮标和杆状浮标的优点，能够高精度测量所在海域的瞬时海面高，而且能够对测量的数据进行姿态补偿。浮标GNSS天线高经近岸同步验潮检验精度可达1 cm，动态海面高测高精度达到2 cm[32]。

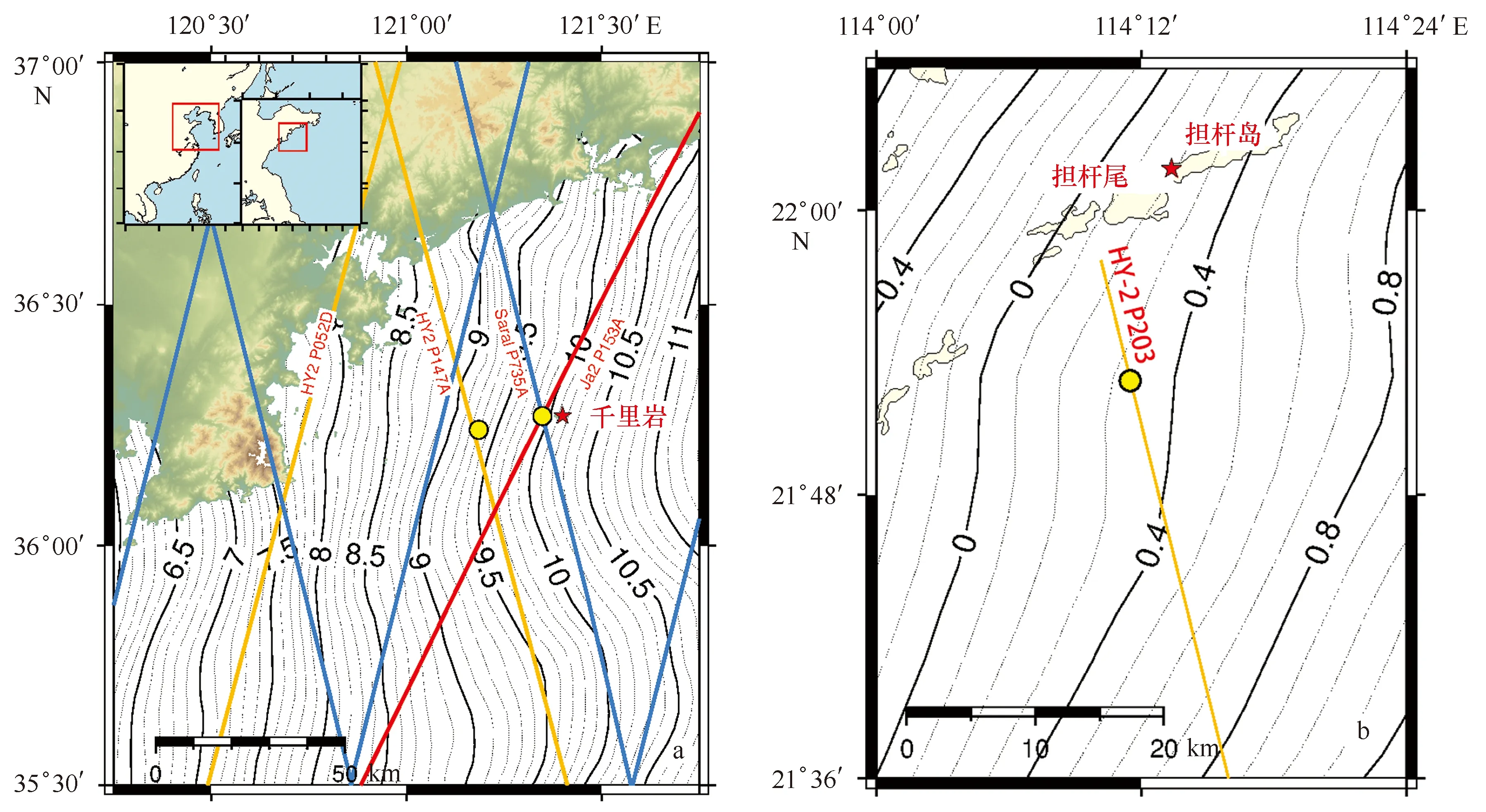
图1 定标千里岩海域(a)和珠海担杆岛海域(b)卫星轨迹分布和浮标布放点，等值线为DTU平均海面高度Fig.1 Satellite ground tracks and GNSS buoy locations at the Qianliyan (a) and Dangan (b) calibration sites，the isoline is from the DTU MSS model

日期过境时间卫星轨道周期号定标点经纬度2014-07-0805:33SaralP735A1436.250°N,121.350°E2014-07-0819:00Jason-2P153A22136.250°N,121.350°E2014-09-1605:33SaralP735A1636.250°N,121.350°E2014-09-1604:53Jason-2P153A22836.250°N,121.350°E2014-09-1817:41HY-2AP147A7836.241°N,121.185°E2014-10-1522:50Jason-2P153A23136.070°N,121.240°E2014-10-1617:41HY-2AP147A8036.070°N,121.240°E2015-05-0218:23HY-2AP203A9421.877°N,114.187°E

本文将GNSS浮标接收机的采样频率设置为1 Hz，在卫星过境之前2小时利用测量船移至定标点。由于千里岩GNSS连续运行站的采样频率为30 s，不利于解算1 Hz的浮标数据，因此在千里岩山顶一处控制点布设一台GNSS参考站，采样率设置为1 Hz，为获得其精确三维坐标持续观测超过4 d时间。该参考站将用于解算浮标动态坐标，并与千里岩验潮井进行精密水准连测，使验潮的水位观测基准统一到WGS-84椭球参考面。在珠海担杆岛的定标试验中GNSS参考站架设在担杆尾，观测时长超过5 d，其参数设置同千里岩参考站。

3.2 GNSS数据解算

GNSS数据处理分为2部分，首先将GNSS参考站的绝对位置坐标在与测高卫星(Jason-2，Saral和HY-2A)一致的ITRF2008框架下进行解算，这一步主要为解算GNSS浮标SSH定义基准，其次是采用GNSS动态解算技术计算GNSS浮标的SSH连续观测结果。

GNSS参考站坐标利用麻省理工学院开发的GAMIT/GLOBK[33—34]解算，参与千里岩参考站解算的区域IGS(International GNSS Service)站分布如图2所示。由于GAMTI解算方案已经趋于标准化[12,35]，本次试验的GNSS数据处理也采用标准化的处理策略，主要参数设置为：基线处理模式RELAX(松弛解)，电离层延迟模型为LC-HELP观测值，对流层模型为Saastamoninen，光压模型为BERN模型，固体潮改正IERS03，考虑到海洋潮汐对解算结果的影响，数据解算时引入全球海潮模型FES2004改正。GLOBK分析得到的GNSS参考站的大地高精度为±9.3 mm。

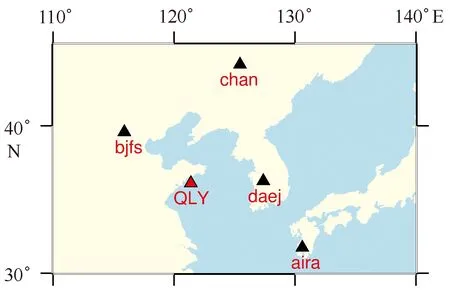
图2 参考站解算所用IGS站点分布Fig.2 Distribution of the IGS sites used in processing reference station

GNSS浮标的解算采用麻省理工学院开发TRACK软件[36]，它属于GAMIT/GLOBK软件包中的一个动态双差定位模块，可以解算每一个历元的GNSS天线相位中心三维坐标、接收机钟差以及大气延迟改正等，通过TRACK解算得到的GNSS浮标SSH精度估计可优于20 mm[7]。利用其解算浮标动态数据时选择的数据处理策略为：选择一个稳固且坐标精确已知的基准站，基于GNSS双差定位模型消除接收机钟差、卫星钟差等未知参数，采用双频无电离层组合方法消除电离层一阶项的折射影响，并在处理过程中加入接收机和卫星天线相位中心位置偏差、固体潮及大气延迟等多项改正，最后采用卡尔曼滤波法逐历元进行参数估计，得到GNSS浮标和参考站之间的坐标差值，并进一步得到ITRF2008框架下的GNSS浮标1 Hz海面高度。

利用TRACK解算浮标数据获得的瞬时海面高时间序列包含长周期潮位变化、中长周期的潮波、海浪的变化以及短周期的浮标上下起伏变化，本文采用姿态改正和“滑动平均”低通滤波方法消除这些因素的影响，其中姿态改正数据来自浮标姿态传感器，浮标SSH的解算结果例子如图3所示。

图3 GNSS浮标解算结果示例Fig.3 Example of the GNSS buoy SSH solutionsa.4 h时长的浮标SSH时间序列，曲线表示滤波后的浮标SSH序列，竖线表示卫星过境时刻; b.卫星过境前后5 min的时间序列a. Four hours’ time series of GNSS buoy measured SSH, in which the curve line shows the filtered SSH and the vertical line shows the satellite passing time；b. five minutes’ time series of SSH before and after satellite passing through

3.3 验潮资料

本文采用的验潮数据为10 min采样数据，时间跨度为2013年11月至2014年7月，覆盖了HY-2A第56周期至73周期观测区间。由于千里岩验潮站高程基准面是独立参考面，本研究通过精密水准连测获得了验潮基本水准点和GPS控制点之间的高差，将验潮海面高归算到WGS-84参考椭球。基本水准点和GPS点的距离约100 m，水准测量闭合差为1 mm，具有较高的精度。由于927大地水准面模型主要是通过船测重力以及测高数据反演得到，是我国近海高精度大地水准面模型，且通过和GNSS浮标实测数据的比较，二者的一致性要优于DTU模型，因此本文将利用该模型用于验潮资料定标方法中的高程传递。

3.4 GNSS浮标测量与模型精度评定

利用在千里岩海洋观测站设立的长期验潮仪对GNSS浮标观测的海面高做了精度验证，由于千里岩海域大地水准面具有显著梯度变化，本文分别利用平均海面高模型DTU10和我国927测绘工程提供的我国近岸大地水准面模型(927模型)进行海面梯度改正，并且通过多点浮标实测数据检验两种模型的相对精度。图4表示放置在Jason-2和Saral交叉点位置以及HY-2A星下点的浮标SSH与验潮站的比较，二者分别距离千里岩验潮站约2 km和20 km。图5表示验潮站与GNSS浮标SSH具体的差异时间序列，其中图5a表示2 km处的浮标与验潮站差异，统计表明采用DTU10模型改正后的二者差异为(3.6±2)cm，采用927模型改正则二者差异为(2.2±2)cm。图5b为20 km处的SSH差异分布，显然是有趋势变化的，这主要是由于20 km的距离将带来显著的潮汐特征差异(2 km处的差异在毫米级，因此影响可忽略不计)，因此必须进行潮汐改正才可以比较。本文利用了中国近海精度较高的NAO.99Jb潮汐预报模型进行潮汐差异分析与改正，图5c表示对浮标SSH进行潮汐差异的补偿改正结果，其中曲线表示浮标SSH原始值，两侧竖线表示潮汐差异的改正量，改正之后浮标和验潮站的差异分布变为图5d，可见加改正之前存在的趋势已得到消除，统计表明经过DTU10模型改正后的二者差异为(-2±2)cm，采用927模型则差异为(1.2±2)cm。结论表明20 km和2 km处的浮标SSH测量均具有约2 cm的精度，与验潮站测量较好符合。另外研究发现采用DTU模型改正后2 km和20 km处的差异均值之差为5.6 cm，若采用927模型二者差异仅为1 cm，说明在我国近岸927大地水准面模型精度优于DTU10模型。

图4 验潮站和GNSS浮标SSH比较Fig.4 The SSH time series of tide gauge and the GNSS buoy

4 高度计数据处理与定标方法

4.1 高程基准统一

GPS卫星采用的参考椭球是WGS-84参考椭球(长轴6 378 137m，扁率1/ 298. 257 223 563)，HY-2A、Jason-2和Saral卫星则采用的T/P椭球参数(长轴6 378 136.3 m，扁率1/298.257)，因此需要将卫星测高数据与GNSS浮标以及验潮资料统一参考椭球。

由参考椭球参数不一致引起的海面高差异可利用下面的计算公式计算：

(1)

4.2 测高数据处理与绝对偏差计算

基于验潮站或者GNSS浮标定标的测高数据处理方法基本一致，卫星测高数据处理主要包括沿轨最近点(PCA)的位置确定和PCA点SSH的内插确定，其中PCA点指距GNSS浮标或者验潮站最近的沿轨星下点。国外研究者对高度计定标中的卫星数据处理与绝对偏差计算方法做了深入研究，制定了较为优化的处理策略，本文的测高数据处理(包括内插方法、改正项处理等)主要参考Mertikas发表的研究成果[18,37]，计算高度计星下点PCA位置的SSH与高度计绝对偏差的主要流程如下：

(1)读取GDR数据集中的1 Hz干延迟、湿延迟、电离层延迟和海况偏差的位置和数值。对于HY-2A，由于第73周期后的干湿延迟值无效，故在浮标定标方法中采用GNSS浮标反演的大气对流层总延迟替代，而基于验潮资料的定标方法中则选择HY-2A第56至73周期数据质量较好的IGDR数据进行研究。

图5 验潮站与GNSS浮标的SSH差异和潮汐改正(a表示2 km处差异，b表示20 km处差异，c表示对20 km处浮标的潮汐改正，d表示正后的20 km处差异)Fig. 5 SSH difference between the tide gauge and the GNSS buoy deployed 2 km (a) and 20 km (b) from the island; tide correction for the GNSS buoy at the 20 km location (c);SSH difference between tide gauge and GNSS buoy after corrected by tide model (d)

(2)读取定标点两侧高频的Ku(20 Hz)或Ka波段(40 Hz)测距值和卫星高度值。

(3)参考(I)GDR产品手册，过滤异常值。

(4)通过统计分析消除1 Hz改正参数数据中可靠性较差的部分。

(5)对1 Hz地球物理改正参数进行多项式拟合，并内插出20 Hz或者40 Hz的改正参数。

(6)使用20 Hz或者40 Hz的改正参数对高频距离值进行改正。

码头拆除前，施工船舶在码头附近开挖抛锚较为困难，可采用抛设备用锚的方式：乘高潮时用锚艇将备用锚抛至码头后方，将锚上的钢丝绳引至码头海侧放置，并设置浮标标示，抓斗船抛锚时，将船上锚缆与已抛备用锚锚缆对接即可。在码头沉箱拆除一段后，锚艇可正常出入码头后方，此时可直接采用锚艇将锚抛至码头后方，不再需要抛设备用锚。

(7)对高频距离值进行分析，消除异常值和不可靠值。

(8)对高频的距离值进行平滑处理，内插出PCA点的距离值。

(9)读取(I)GDR中高频卫星轨道高度，并进行平滑处理，内插出PCA点轨道高度。

(10)读取(I)GDR中1 Hz潮汐相关改正参数，包括固体潮、极潮、海洋载荷潮，并内插到PCA位置。

(11) 高度计PCA点的SSH可用式(2)计算：

SSHAlt=hAlt-(rAlt+rCorr+TLCorr)，

(2)

式中，hAlt为高度计轨道的椭球高；rAlt为高度计的距离观测量；rCorr为距离总改正(干湿延迟、电离层延迟、SSB)；TLCorr为潮汐相关改正(固体潮、极潮、Ocean Loading Tide等)。

(13)浮标和PCA点距离较近，因此不对海洋潮汐差异特征进行改正。利用验潮资料定标时需要利用NAO.99Jb模型对潮汐差异进行改正。

(14)按照下面的公式可获得卫星测高的绝对偏差：

SSHbias=SSHAlt-SSHinsitu，

(3)

式中，SSHAlt表示卫星测高PCA点的海面高度；SSHinsitu表示卫星过境时刻的GNSS浮标海面高或者验潮海面高；SSHbias表示高度计的绝对偏差。

5 定标结果

通过2014-2015年的GNSS浮标定标试验，得到了HY-2A以及Jason-2、Saral卫星高度计多个周期的绝对偏差。表2为浮标定标结果，其中Jason-2采用的数据版本是GDR-d，试验得到了3个周期的绝对偏差，其均值为5.7 cm，与希腊定标场2013年公布的结果2 cm[38]差异为3.7 cm。Saral的数据版本是GDR-T，试验共获得了2个周期的绝对偏差，其均值为-2.2 cm，与希腊定标场2015年公布的结果-4.6 cm[18]相差约2.4 cm。本文试验中的GNSS参考站大地高精度约为±9 mm，浮标动态双差解算精度为20 mm，最终GNSS浮标海面高观测精度估计为±22 mm，另外考虑卫星测高SSH的测量精度估计为2～3 cm，因此浮标定标结果精度约为3.0～3.7 cm，得到的Jason-2和Saral高度计绝对偏差与希腊定标场的结果差异基本在观测误差影响之内。

表2 高度计定标结果

注：“-”表示无实验数据。

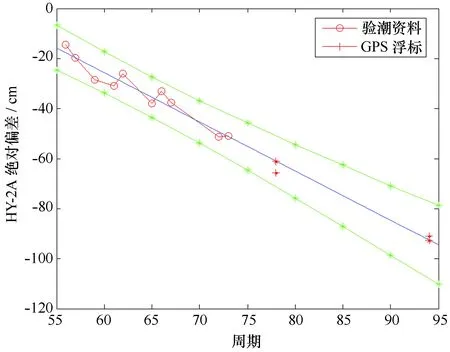
图6 基于验潮资料和GNSS浮标的HY-2A定标结果Fig.6 Calibration result of HY-2A based on tide gauge data and GNSS buoy

本文中HY-2A采用的是国家卫星海洋应用中心公布的临时地球物理数据IGDR，使用浮标定标方法得到了2个周期的有效定标结果，分别是第78周期的绝对偏差-65 cm，第94周期的绝对偏差-91 cm。本文利用千里岩验潮资料对HY-2A第56至73周期的定标结果如图6所示，结果发现存在显著的漂移，其漂移速率为-51 cm/a，图6绘出了基于验潮资料计算的置信度为95%的HY-2A绝对偏差线性回归分析结果，结果表明HY-2A的GNSS浮标定标值均在预测区间内，其中第78周期浮标定标值与验潮资料预测值相差-4.7 cm，第94周期相差1.7 cm，两种不同定标方法得到的结果具有一致性。经过与国家卫星海洋应用中心和国家空间科学中心沟通，确定SSH漂移主要原因是由于高度计星上的超稳振荡器(ultrastable oscillator，简称USO)漂移造成的，USO的漂移对卫星高度计测距产生了直接影响，进而影响SSH。Wan等利用陆地有源定标器观测到HY-2A的USO漂移导致的卫星测距漂移速率为-40 cm/a[19]，与本文的定标结果基本符合，差异原因可能在于所用数据时间长度不同，另外高度计偏差除了USO漂移外还存在其他误差源带来的叠加效应(如星载微波校正辐射计)。本文结果与希腊专门定标场对HY-2A 第54至62周期的SGDR数据定标结果进行比较，但由于其采用的HY-2A数据时间较短，其论文未对HY-2A的漂移进行定量计算，仅给出了HY-2A绝对偏差均值为(-27±3) cm[18]，若统计本研究第56周期至62周期HY-2A 绝对偏差则为(-24.1±6.7) cm，二者差异小于3 cm。

6 结论

本文利用GNSS浮标和千里岩验潮资料对HY-2A等多颗高度计进行定标研究，通过同步验潮站检验表明GNSS浮标的SSH测量精度在2 cm左右，满足高度计的定标需求。本文首先利用GNSS浮标对已知海面高偏差的国外高度计Jason-2和Saral做了定标研究，结果与希腊Crete定标场结果符合较好，差异在测量误差范围内。由于利用GNSS浮标获得的HY-2A定标结果较少，本文又利用千里岩验潮资料分析了HY-2A IGDR第56周期至73周期的绝对偏差，回归分析结果表明HY-2A IGDR数据的SSH存在约-51 cm/a的漂移，且浮标和验潮资料得到的HY-2A漂移具有一致性，其海面高偏差从2013年11月的-14 cm变为2015年5月的-91 cm，并在该时期内呈现出显著的线性规律。结合已发表的地面有源定标器定标结论，确定USO漂移是造成HY-2A卫星高度计SSH线性漂移的主要原因。由于SSH观测误差的多元性，HY-2A的SSH漂移可能包含其他因素，例如星载微波校正辐射计观测的大气湿延迟，因此在未来的工作中需对此开展研究，进一步的量化各SSH误差源。

由于目前我国仍未建立专门的高度计定标场，本研究利用了GNSS浮标和验潮资料对HY-2A IGDR定标，开展了相关的现场测量工作，首次通过海上绝对定标获得了HY-2A卫星高度计的测高偏差以及漂移速率，将为HY-2A 测高数据的误差修正和升级提供依据，对我国后续海洋卫星高度计的定标以及未来定标场的建设提供参考。

致谢：感谢千里岩海洋观测站工作人员在试验期间给予的生活帮助，法国AVISO提供Jason-2和Saral/AltiKa的GDR数据，国家卫星海洋应用中心提供HY-2A的IGDR数据。与希腊克里特理工大学Mertikas教授的讨论也对本文非常有益，在此表示感谢。

[1] 蒋涛, 李建成, 王正涛, 等. 联合Jason-1与Grace卫星数据研究全球海平面变化[J]. 测绘学报, 2010, 39(2): 135.

Jiang Tao, Li Jiancheng, Wang Zhengtao, et al. Global sea level variations from combined Jason-1 and Grace data[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(2): 135.

[2] Sandwell D T, Mller R D, Smith W H F, et al. New global marine gravity model from Cryosat-2 and Jason-1 reveals buried tectonic structure[J]. Science, 2014, 346(6205): 65-67.

[3] 蒋兴伟, 林明森, 张有广. HY-2卫星地面应用系统综述[J]. 中国工程科学, 2014, 16(6): 4-12.

Jiang Xingwei, Lin Mingsen, Zhang Youguang. An overview of HY-2 satellite ground application system[J]. Engineering Sciences, 2014, 16(6): 4-12.

[4] Bao L, Gao P, Peng H, et al. First accuracy assessment of the HY-2A altimeter sea surface height observations: cross-calibration results[J]. Advances in Space Research, 2015, 55(1): 90-105.

[5] 杨磊, 周兴华, 彭海龙, 等. 基于Jason-2的Saral/AltiKa高度计全球统计评估与交叉定标[J]. 海洋科学进展, 2014, 32(4): 482-490.

Yang Lei, Zhou Xinghua, Peng Hailong, et al. Saral/AltiKa global statistic assessment and cross-calibration with Jason-2[J]. Advances in Marine Science, 2014, 32(4): 482-490.

[6] 鲍李峰，陆洋. 西太平洋海域卫星测高重力垂直梯度分布[J]. 武汉大学学报 (信息科学版), 2005, 30(9): 68-71.

Bao Lifeng, Lu Yang. Distribution of vertical graident of altimetry gravity in the Western Pacific[J]. Geomatics and Information Science of Wuhan University, 2005, 30(9): 68-71.

[7] Bonnefond P, Exertier P, Laurain O, et al. Saral/AltiKa absolute calibration from the multi-mission corsica facilities[J]. Marine Geodesy, 2015(S1): 171-192.

[8] Fu L-L，Haines B J. The challenges in long-term altimetry calibration for addressing the problem of global sea level change[J]. Advances in Space Research, 2013, 51(8): 1284-1300.

[9] Christensen E J, Haines B J, Keihm S J, et al. Calibration of TOPEX/Poseidon at platform harvest[J]. Journal of Geophysical Research: Oceans, 1994, 99(C12): 24465-24485.

[10] Haines B J, Dong D, Born G H, et al. The Harvest experiment: monitoring Jason-1 and TOPEX/Poseidon from a California offshore platform special issue: Jason-1 calibration/validation[J]. Marine Geodesy, 2003, 26(3/4): 239-259.

[11] Haines B J, Desais D, Born G H. The Harvest experiment: calibration of the climate data record from Topex/Poseidon, Jason-1 and the ocean surface topography mission[J]. Marine Geodesy, 2010, 33(S1): 91-113.

[12] Watson C, Coleman R, White N, et al. Absolute calibration of TOPEX/Poseidon and Jason-1 using GPS buoys in Bass Strait, Australia special issue: Jason-1 calibration/validation[J]. Marine Geodesy, 2003, 26(3/4): 285-304.

[13] Watson C, White N, Coleman R, et al. TOPEX/Poseidon and Jason-1: absolute calibration in Bass Strait, Australia[J]. Marine Geodesy, 2004, 27(1/2): 107-131.

[14] Watson C, White N, Church J, et al. Absolute calibration in Bass Strait, Australia: TOPEX, Jason-1 and OSTM/Jason-2[J]. Marine Geodesy, 2011, 34(3/4): 242-260.

[15] Bonnefond P, Exertier P, Laurain O, et al. Absolute calibration of Jason-1 and TOPEX/Poseidon Altimeters in corsica special issue: Jason-1 calibration/validation[J]. Marine Geodesy, 2003, 26(3/4): 261-284.

[16] Bonnefond P, Exertier P, Laurain O, et al. Absolute calibration of Jason-1 and Jason-2 altimeters in Corsica during the formation flight phase[J]. Marine Geodesy, 2010, 33(S1): 80-90.

[17] Pavlis E C, MertiKas S P. The Gavdos mean sea level and altimeter calibration facility: results for Jason-1[J]. Marine Geodesy, 2004, 27(3/4): 631-655.

[18] Mertikas S P, Zhou X, Qiao F, et al. First preliminary results for the absolute calibration of the Chinese HY-2 altimetric mission using the CRS1 calibration facilities in West Crete, Greece[J]. Advances in Space Research, 2015, 57(1): 78-95.

[19] Wan J, Guo W, Zhao F, et al. HY-2A radar altimeter ultrastable oscillator drift estimation using reconstructive transponder with its validation by multimission cross calibration[J]. Geoscience and Remote Sensing, IEEE Transactions on, 2015(9): 5229-5236.

[20] 彭海龙, 林明森, 穆博, 等. HY-2A卫星雷达高度计数据的全球统计评价及质量分析[J]. 海洋学报, 2015, 32(7): 54-66.

Peng Hailong, Lin Mingsen, Mu Bo, et al. Global statistical evaluation and performance analysis of HY-2A satellite radar altimeter data[J]. Haiyang Xuebao, 2015, 32(7): 54-66.

[21] 彭海龙. HY-2A卫星雷达高度计定标检验关键技术研究[D]. 青岛: 中国海洋大学, 2015.

Peng Hailong. Key technology of HY-2A satellite altimeter calibration[D]. Qingdao：Ocean University of China, 2015.

[22] 杨磊, 周兴华, 林明森, 等. HY-2A卫星雷达高度计全球IGDR数据质量评估[J]. 地球物理学进展, 2016, 31(2): 0629-0636.

Yang Lei, Zhou Xinghua, Lin Mingsen,et al. Global statistical assessment and cross-calibration of HY-2A satellite radar altimeter[J]. Progress in Geophysics, 2016, 31(2): 0629-0636.

[23] Chen W, Hu C, Li Z, et al. Kinematic GPS precise point positioning for sea level monitoring with GPS buoy[J]. Journal of Global Positioning Systems, 2004, 3(1/2):302-307.

[24] Watson C, Coleman R, Handsworth R. Coastal tide gauge calibration: A case study at Macquarie Island using GPS buoy techniques[J]. Journal of Coastal Research, 2008，2(4): 1071-1079.

[25] Born G H, Parke M E, Axelrad P, et al. Calibration of the TOPEX altimeter using a GPS buoy[J]. Journal of Geophysical Research: Oceans, 1994, 99(C12): 24517-24526.

[26] Key K W, Parke M E, Born G H. Mapping the sea surface using a GPS buoy[J]. Marine Geodesy, 1998, 21(1): 67-79.

[27] Watson C S. Satellite altimeter calibration and validation using GPS buoy technology[D]. Tasmania: University of Tasmania, 2005.

[28] 徐曦煜, 王振占, 叶沛, 等. GPS浮标数据反演海浪谱的理论仿真与试验验证[J]. 海洋学报, 2014, 36(7): 34-44.

Xu Xiyu, Wang Zhenzhan, Ye Pei, et al. The oretically simulation and campaign validation of ocean wave spectrum retrieval from GPS buoy measurements[J]. Haiyang Xuebao, 2014, 36(7): 34-44.

[29] 陈春涛, 闫龙浩, 张晓旭, 等. 基于 GPS 的高度计海面高度定标浮标设计[J]. 中国工程科学, 2014, 16(6): 109-112.

Chen Chuntao，Yan Longhao，Zhang Xiaoxu, et al. Design of buoy for the calibration of altimeter sea surface height based on GPS[J]. Engineering Sciences, 2014, 16(6): 109-112.

[30] 陈春涛, 翟万林, 张倩, 等. 基于GPS 的测高浮标的设计、研制与测试[J]. 海洋技术学报, 2014, 33(1): 102-108.

Chen Chuntao, Zhai Wanlin, Zhang Qian, et al. Design, manufacture and test of sea surface height buoy for altimeter calibration based on the Global Positioning System[J].Journal of Ocean Technology,2014, 33(1): 102-108.

[31] Dong X, Woodworth P, Moore P, et al. Absolute calibration of the TOPEX/Poseidon altimeters using UK tide gauges, GPS, and precise, local geoid-differences[J]. Marine Geodesy, 2002, 25(3): 189-204.

[32] 周东旭, 周兴华, 梁冠辉, 等. GPS浮标天线高的动态标定方法[J]. 测绘科学, 2015, 40(12): 121-124.

Zhou Dongxu, Zhou Xinghua, Liang Guanhui, et al. Research on dynamic calibration method of GPS buoy antenna heights[J]. Science of Surveying and Mapping, 2015, 40(12): 121-124.

[33] King R, Bock Y. Documentation for the GAMIT GPS Analysis Software[R]. Mass Inst of Technol, Cambridge Mass, 1999.

[34] Herring T, King R, Mcclusky S. GLOBK: Global Kalman Filter Vlbi and GPS Analysis Program Version 10.0[R]. Massachusetts Institute of Technology, Cambridge, MA, 2002.

[35] Herring T, King R, Mcclusky S. Introduction to GAMIT/GLOBK[R]. Massachusetts Institute of Technology, Cambridge, 2008.

[36] Chen G. GPS Kinematic Positioning for the Airborne Laser Altimetry at Long Valley[D]. Boston: Massachusetts Institute of Technology, 1998.

[37] Mertikas S, Ioannides R, Tziavos I, et al. Statistical models and latest results in the determination of the absolute bias for the radar altimeters of Jason Satellites using the Gavdos facility[J]. Marine Geodesy, 2010, 33(S1): 114-149.

[38] Mertikas S. Latest result for the calibration of Jason and HY-2 using Gavodos/Crete permanent calibration facility[R]. OSTST, Boulder , 2013.

Absolute calibration of sea surface height for HY-2A Satellite altimeter by GNSS buoy and tide gauge data

Yang Lei1, Zhou Xinghua1, Wang Zhaoyang1,2, Liang Guanhui1, Tang Qiuhua1,Zhou Dongxu1,2, Lei Ning1,2, Yang Long1, Mu Bo3

(1.FirstInstituteofOceanography,StateOceanicAdministration,Qingdao266061,China; 2.CollegeofGeodesyandGeomatics,ShandongUniversityofScienceandTechnology,Qingdao266590,China；3.NationalSatelliteOceanApplicationService,Beijing100081,China)

In order to determine the absolute bias of HY-2A sea surface height (SSH) and monitor the on-orbit working conditions of HY-2A Satellite altimeter, we conducted the absolute calibration experiments in the Qianliyan and Dangan area of China. In this study we adopted two independent methods which are deploying the GNSS buoy under satellite tracks for simultaneous observation and using the tide gauge data combined with the precise geoid model. In addition, for verifying the accuracy of the GNSS buoy calibration method, the Jason-2 and Saral Satellite altimeters, which were already calibrated by international calibration sites, were also calibrated using the same GNSS buoy. The SSH accuracy of the GNSS buoy is estimated to be about 2 cm by comparison with the tide gauge data. The absolute biases of Jason-2 and Saral calibrated by the GNSS buoy are 5.7 cm and -2.3 cm, which are in accordance with the results of the international calibration sites. According to the GNSS buoy the SSH absolute biases for HY-2 are determined to be -65 cm in September 2014 and -91 cm in May 2015, which are changed significantly for the two experiments. Thus in order to quantify the drift velocity of HY-2A SSH and assess the on-orbit working conditions of HY-2A Satellite altimeter more accurately, we used long time series of tide gauge data of the Qianliyan oceanic station to calibrate the cycles 56 to 73 of HY-2A. The drift phenomenon of HY-2A SSH is confirmed by the long-time series altimeter data and the drift velocity is estimated to be -51 cm/a. By the regression analysis with 95% confidence coefficient, the GNSS buoy calibration result of HY-2A is in good accordance with the result from the tide gauge data. From the result of this paper, we conclude that under the condition of no dedicate calibration site the altimeter absolute bias could be determined by GNSS buoy with flexibility and high accuracy and the drift of absolute bias could be quantified by the tide gauge data combined with the precise geoid mode.

GNSS buoy； absolute calibration； HY-2A； Saral/AltiKa；Jason-2

10.3969/j.issn.0253-4193.2017.01.012

2016-04-15；

2016-07-14。

国家国际科技合作专项“自主星载高度计海面测高在轨绝对定标关键技术研究”(2014DFA21710);中央级公益性科研院所基本科研业务费专项资金资助项目(GY0214G21, GY0214G23,GY02-2011T05)；开展卫星海洋测绘应用(WX0316005)。

杨磊(1988—)，男，山东省郓城县人，工程师，主要从事海洋测绘研究。E-mail：leiyang@fio.org.cn

*通信作者：周兴华(1964—)，男，博士生导师，研究员，主要从事海洋测绘研究。E-mail：xhzhou@fio.org.cn

P715.6

A

0253-4193(2017)01-0111-10

杨磊，周兴华，王朝阳, 等. 基于GNSS浮标和验潮资料的HY-2A卫星高度计绝对定标[J]. 海洋学报, 2017, 39(1): 111-120,

Yang Lei, Zhou Xinghua, Wang Zhaoyang, et al. Absolute calibration of sea surface height for HY-2A Satellite altimeter by GNSS buoy and tide gauge data[J]. Haiyang Xuebao, 2017, 39(1): 111-120, doi:10.3969/j.issn.0253-4193.2017.01.012