磨刀门河口枯季波生流场数值模拟研究

刘诚，梁燕，彭石，侯堋

(1.珠江水利委员会 珠江水利科学研究院，广东 广州 510611；2. 中交四航勘察设计院有限公司，广东 广州 510230)



磨刀门河口枯季波生流场数值模拟研究

刘诚1，梁燕2，彭石1，侯堋1

(1.珠江水利委员会 珠江水利科学研究院，广东 广州 510611；2. 中交四航勘察设计院有限公司，广东 广州 510230)

本文建立曲线坐标系下的双曲型缓坡方程波浪模型和考虑波浪辐射应力影响的深度平均2D潮流数学模型，首次研究了磨刀门河口2011年地形条件下的枯季波生流场。受波浪作用影响，落潮阶段，波浪作用方向与流向相反，在波浪顶托效应下拦门沙沙脊及外坡处流速普遍减小，形成两个主要回流区，口门外东西两侧浅滩处流速也减小，东西两汊及横洲深槽流速增大；涨潮阶段，波浪作用方向与流向相同，拦门沙沙脊及外坡处流速增大，沙脊处出现冲越流，口门两侧浅滩处流速增大，横洲深槽流速减小。

磨刀门河口；波生流；辐射应力；缓坡方程；深度平均2D潮流模型

1 引言

波生流也称波周期剩余动量，是波浪破碎变形导致的波周期尺度流动现象，其驱动力被Longuet-Higgins解释为波浪辐射应力[1]。国内外波生流方面的数值模拟研究已经取得一定进展，按照所采用波浪模型的不同可分为缓坡方程、Boussinesq方程和波能谱方程。国内李孟国和张大错[2]、Sun和Tao[3]、白志刚和周锡礽[4]、王厚杰和李瑞杰[5]、佟飞飞等[6]基于缓坡方程研究了近岸波生流，王世澎等[7]结合缓坡方程研究波浪对潮流的影响，Wu和Zhang[8]、解鸣晓和张玮[9]、Sun[10]、熊伟等[11]基于缓坡方程开展了三维波生流研究。以上研究采用的模型为抛物型或双曲型缓坡方程，唐军等采用椭圆型缓坡方程模拟近岸波浪变形和波生流[12—14]。房克照等[15]、荆海晓[16]、李绍武和黄筱云[17]、卢吉和余锡平[18]采用Boussinesq方程模拟研究波生流。杨静思[19]、赵张益和张庆河[20]、Zheng和Tang[21]、Liang和Zhao[22]、Xu和Zhang[23]、解鸣晓[24]、王平和张宁川[25]采用波能谱方程耦合不同类型的浅水方程模拟波生流。国外Bennis和Ardhuin[26]回顾了波生流数学模型研究进展。

国内波生流模拟主要以海岸带为研究对象[1—6,8—18,20—21]，假定研究区域在某时段内维持某个潮位不变，较少涉及背景潮汐运动，极少涉及河口区。究其原因，一方面河口区受潮流和径流影响较大，波生流的重要性被弱化。另一方面，添加波浪辐射应力后，浅水方程求解难收敛，流场不稳定[27]；针对此原因，包四林等[28]采用改进的Hardy-Cross法模拟波生流场。

珠江磨刀门河口为弱潮河口，受口门整治工程影响，其正在由径流优势型河口向径流-波浪型河口转变[29]，波浪对其影响逐步增强[30]。在枯季，磨刀门河口径流量小，波浪动力强，海洋动力对河口控制作用占优势，河口地貌具有典型浪控形态和波生流塑造特征。胡达等[31]认为磨刀门口外西侧交杯沙是拦门沙在SE向浪作用下向西搬运的产物。

为研究波浪对枯季磨刀门河口潮流的影响，本文将佟飞飞等不考虑背景潮汐运动的波生流数学模型[6,32]扩展至弱潮河口区，建立曲线坐标系下考虑波浪影响的潮流数学模型；作者曾将本模型用于模拟海南南渡江河口的波浪潮流泥沙运动[33]。论文首先通过典型算例验证了波生流模型的有效性，然后将其首次用于模拟枯季磨刀门河口波生流，研究分析波浪对该河口潮流的影响。对于磨刀门河口的水动力研究，以往多以径流、潮流及咸潮运动为主[29]，尚未开展波浪对潮流的影响及河口波生流方面的数值模拟研究。

2 模型介绍

采用贴体正交曲线坐标系推导二维水流控制方程，设正交曲线坐标系内一点(ξ，η)与直角坐标系内一点(x，y)之间的关系如下：ξ=ξ(x,y)，η=η(x,y)。对于直角坐标系内某一变量φ，其导数变换为：φx=φξξx+φηηx，φy=φξξy+φηηy，令 J=yηxξ-xηyξ，ξx=yη/J，ξy=-xη/J，ηx=-yξ/J，ηy=xξ/J。

2.1 波浪模型

对直角坐标系下的模型控制方程进行坐标变换，则用于模拟波浪运动的正交曲线坐标系下的双曲型缓坡方程控制方程为：

(1)

(2)

(3)

式中，C和Cg为波浪传播相速度和群速度；H为波高函数；P和Q为曲线坐标系下的波浪水质点沿水深积分的速度函数；P=Qxyη-Qyxη；Q=Qxxξ-Qyyξ；Qx和Qy为直角坐标系的波浪水质点水深积分速度函数。模型边界条件、离散和求解过程详见文献[6,32]。

2.2 潮流模型

同样地，可以得到曲线坐标系下考虑波浪影响的潮流控制方程的通用形式以及变量取值，如式(4)所示，公式中的具体变量见表1。

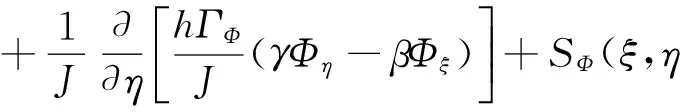
(4)

表1 曲线坐标系下考虑波浪影响的二维水流数学模型控制方程通用形式的变量

其中，

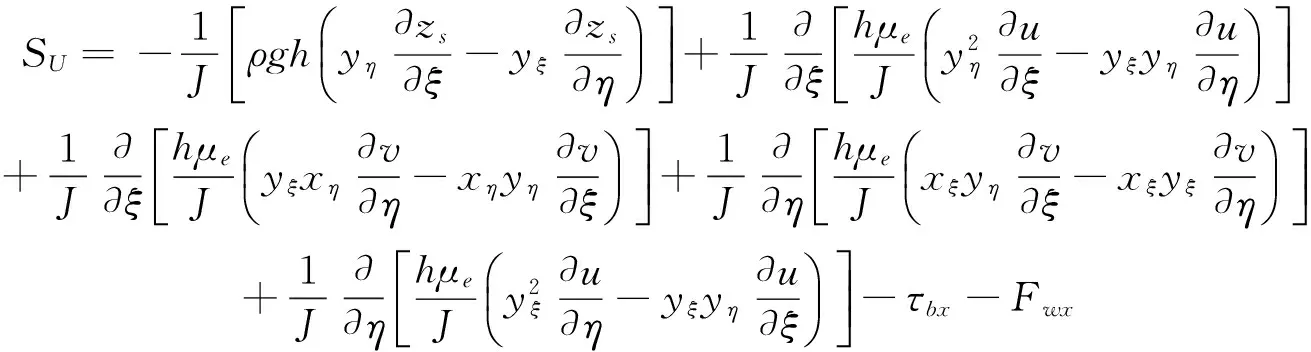
(10)

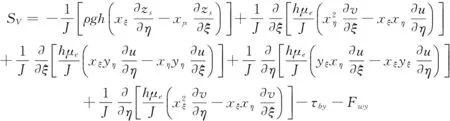
(11)

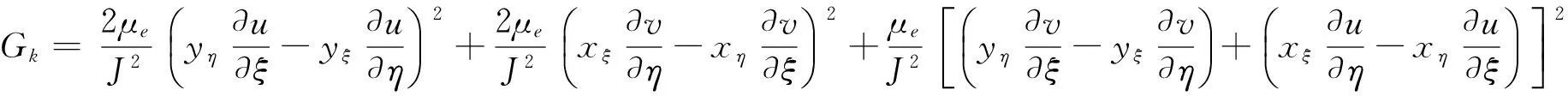
(12)

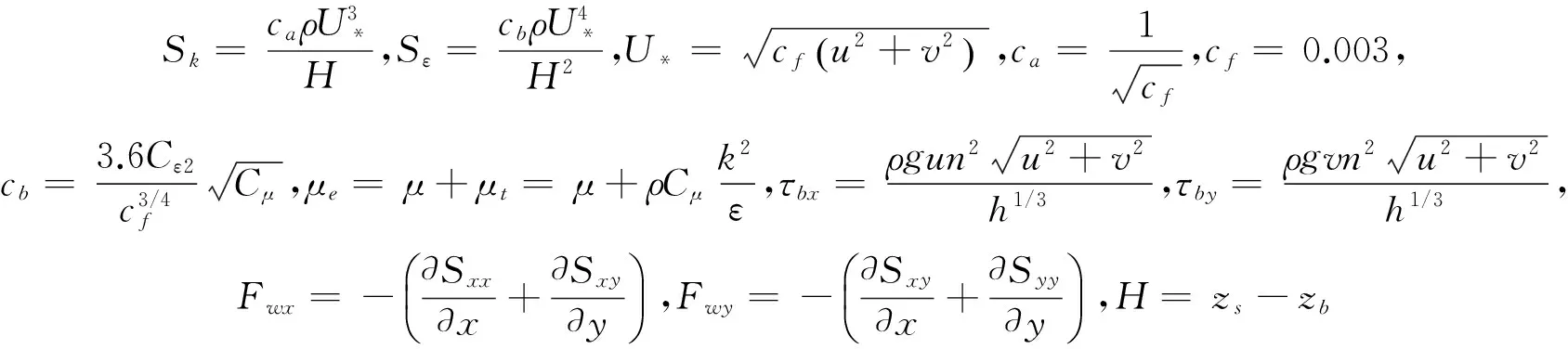
式中，Φ为控制方程通用形式中主要变量的统一代表符号；ΓΦ和SΦ分别为方程通用形式中湍动扩散系数以及源项的统一代表符号；x、y和ξ、η分别为直角坐标系下和曲线坐标系下的坐标；U、V为ζ、η方向流速分量；u、v为x、y方向流速分量；Fwx、Fwy为波浪对水体的作用力；zs为水面高程，zb为水底高程；h为水深；ρ为密度；g为重力加速度；μ为水动力黏性系数，μt为水运动涡黏性系数；n为河床底部糙率，n=n0+nk/h，nk=0.05；Cε1=1.45、Cε2=1.92、Cμ=0.09、σk=1.0、σε=1.3为k-ε湍流模型引入的参数。模型边界条件、离散和求解过程参照文献[32—33]。

3 模型验证

Hamm[34]1992年实验研究了波浪在单个凹型斜坡地形上传播、破碎及波生流的生成和分布，实验水槽尺寸为30 m×30 m，斜坡坡度为1∶30，在此斜坡上经开挖形成凹型水槽，凹型斜坡地形的水深平面分布由式(13)确定。

(13)

Sørensen等[35]对Hamm实验进行数值模拟研究，研究工况之一为入射波高H=0.07 m，周期T=1.25 s的规则波在该地形条件下形成的波生流。采用本文模型进行波生流数值计算，网格尺寸为0.3 m×0.3 m。图1为未考虑流速对波浪影响的波生流场计算结果，图2为文献[35]中Sørensen的数值模拟结果[35]，图1和图2的一致性良好。图3和图4比较了沿y=15 m处的波高和波生流计算结果和实验测量结果，可知近岸波高随着水深的变浅先增大再骤减，波浪破碎变形后形成波生流。数学模型计算结果较好地模拟了Hamm实验中的波浪和波生流分布。

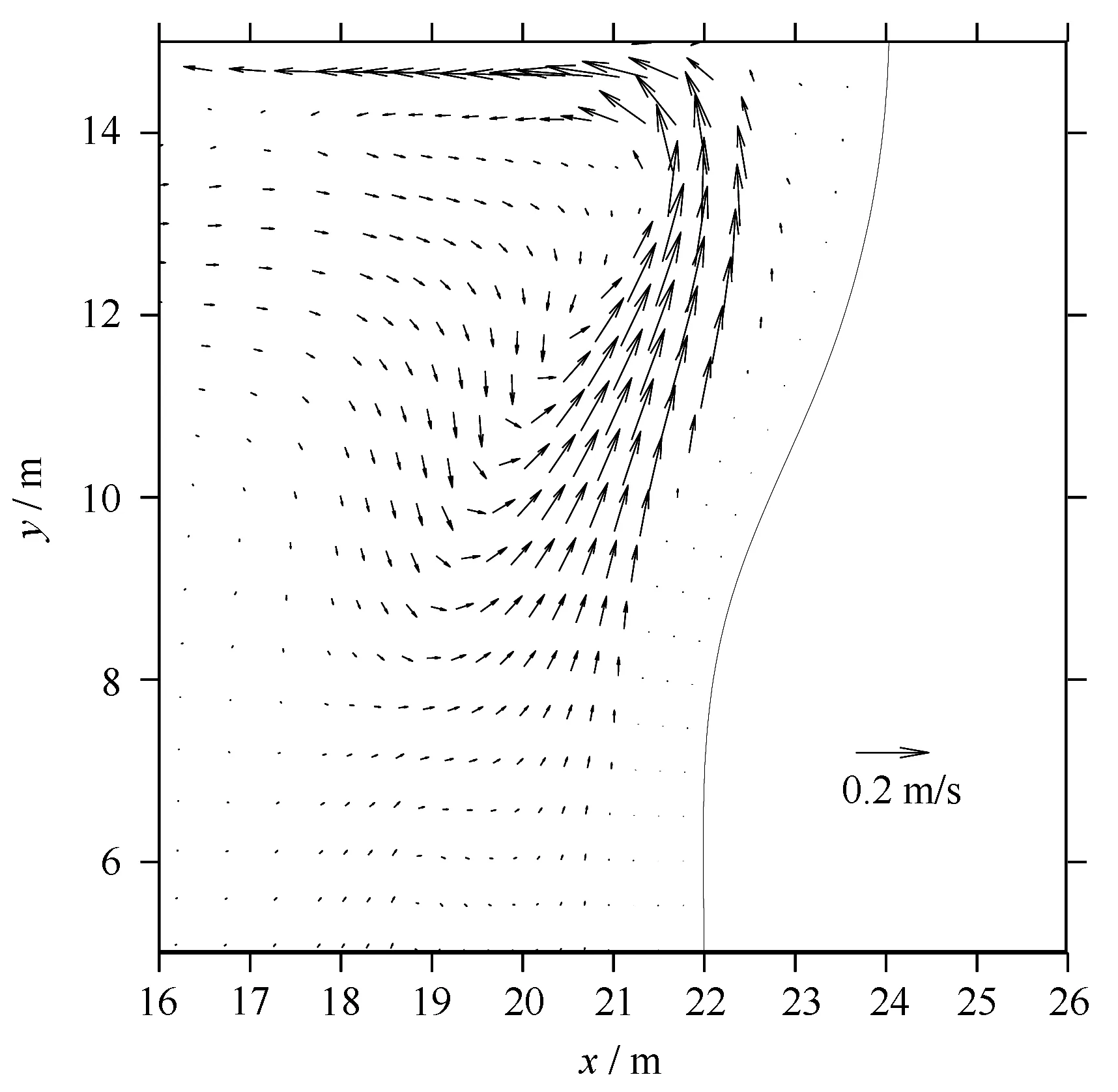
图1 Hamm实验[34]本文波生流模拟结果Fig.1 The numerical result of wave induced current for Hamm experiments[34]

图2 文献 [35] 的Hamm实验波生流结果Fig.2 Sørensen’s numerical result[35] of wave induced current for Hamm experiments

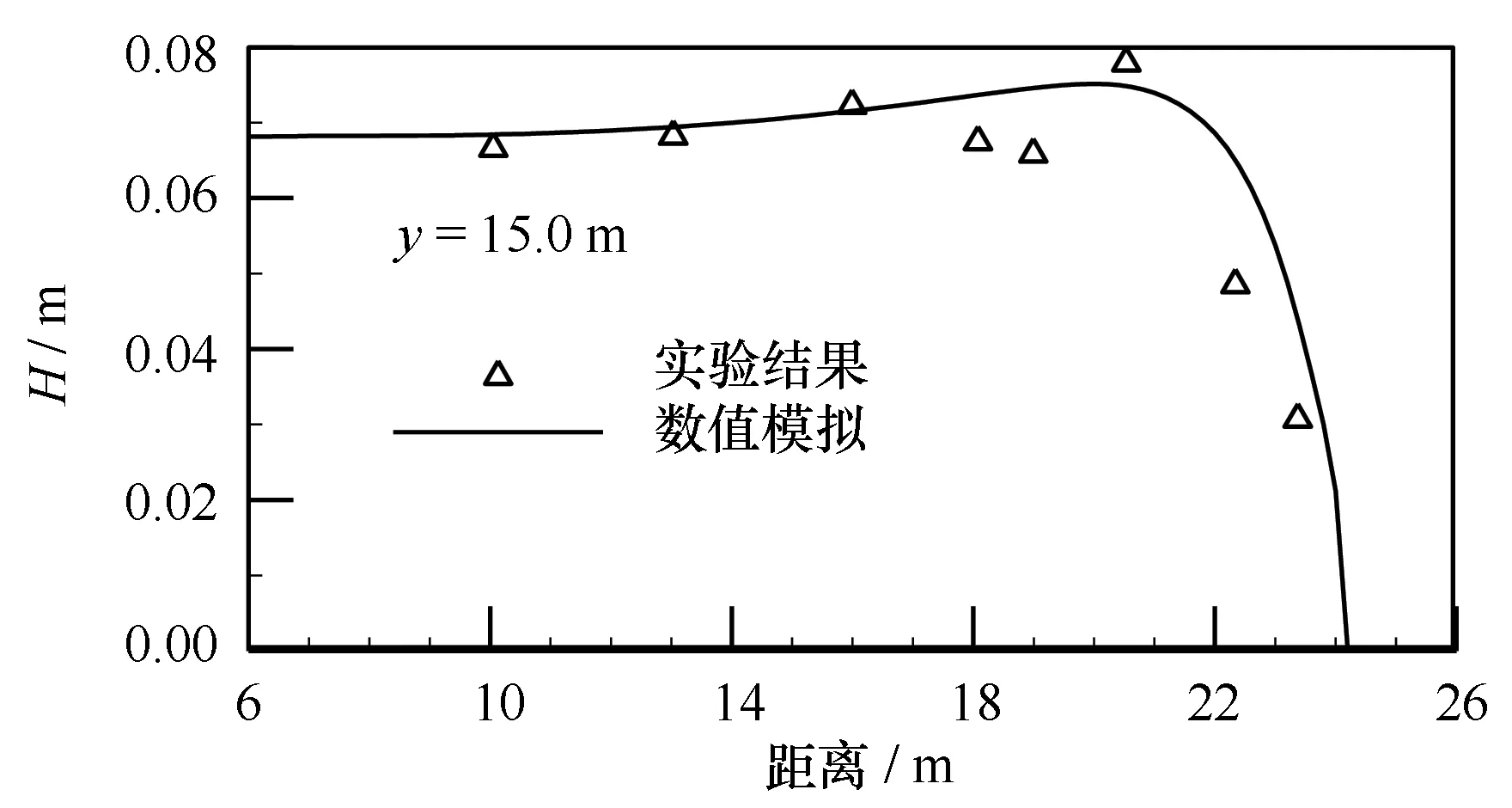
图3 Hamm实验[34-35]中y=15 m轴线处的波高变化本文数值模拟结果与实验结果比较Fig.3 The wave height comparison between numerical and experimental data for Hamm experiments[34—35]

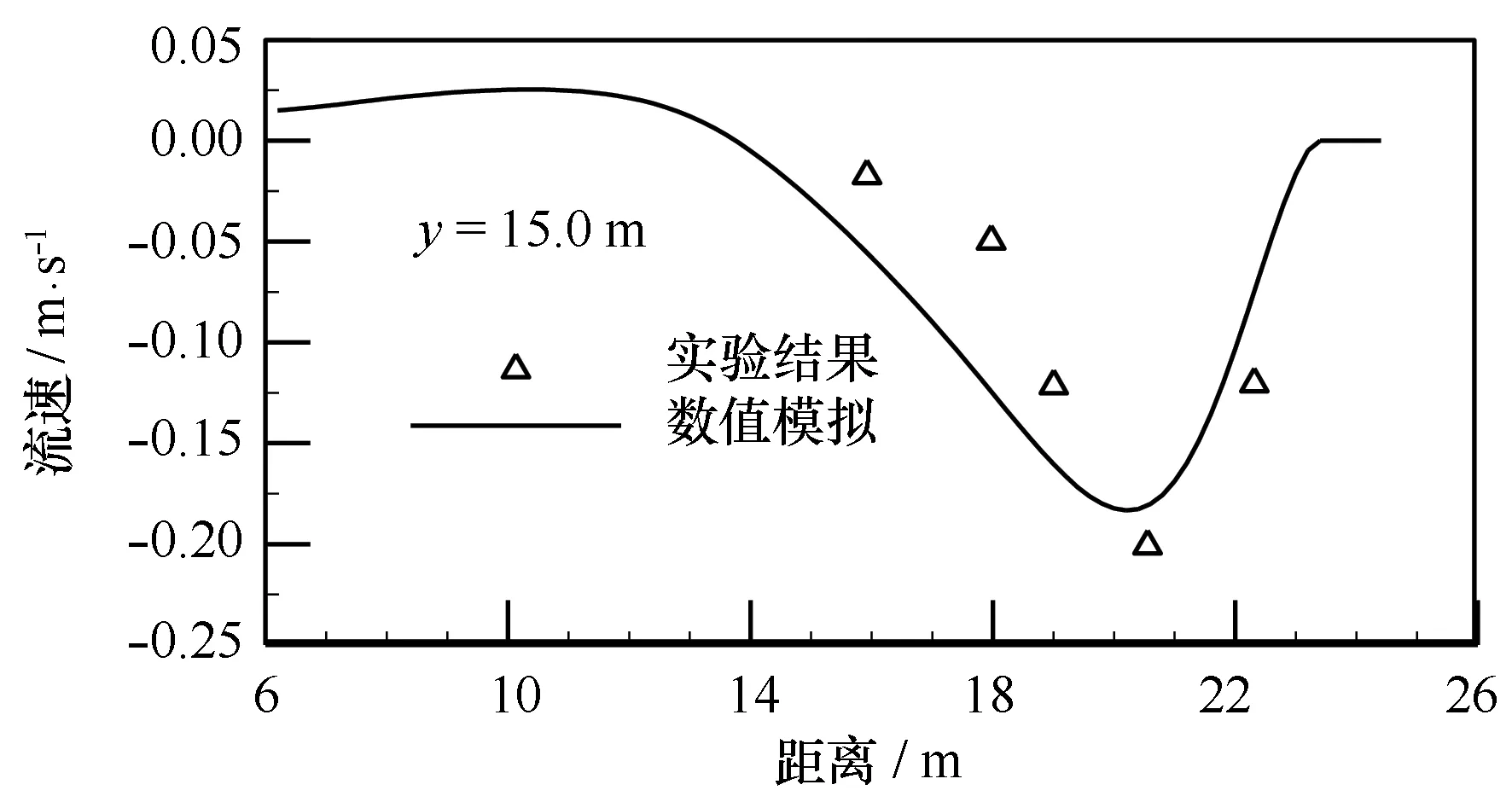
图4 Hamm实验[34—35]中y=15 m轴线处波生流变化本文数值模拟结果与实验结果比较Fig.4 The wave induced current comparison between numerical and experimental data for Hamm experi-ments[34-35]

4 枯季磨刀门河口波生流场及波浪对潮流的影响

枯季磨刀门河口波生流研究采用2011年实测地形(图5)，模型外边界为25 m等深线，两侧边界覆盖黄茅海和伶仃洋，上边界至灯笼山水文站，网格数为781×681，最小网格尺寸为50 m×50 m。模型含上游径流、外海潮汐及波浪3类边界。图6为低高潮时刻(与图9对应)的波高分布情况。

图5 磨刀门河口2011年地形图(珠江基面)Fig.5 The topography of Modaomen estuary in the year 2011

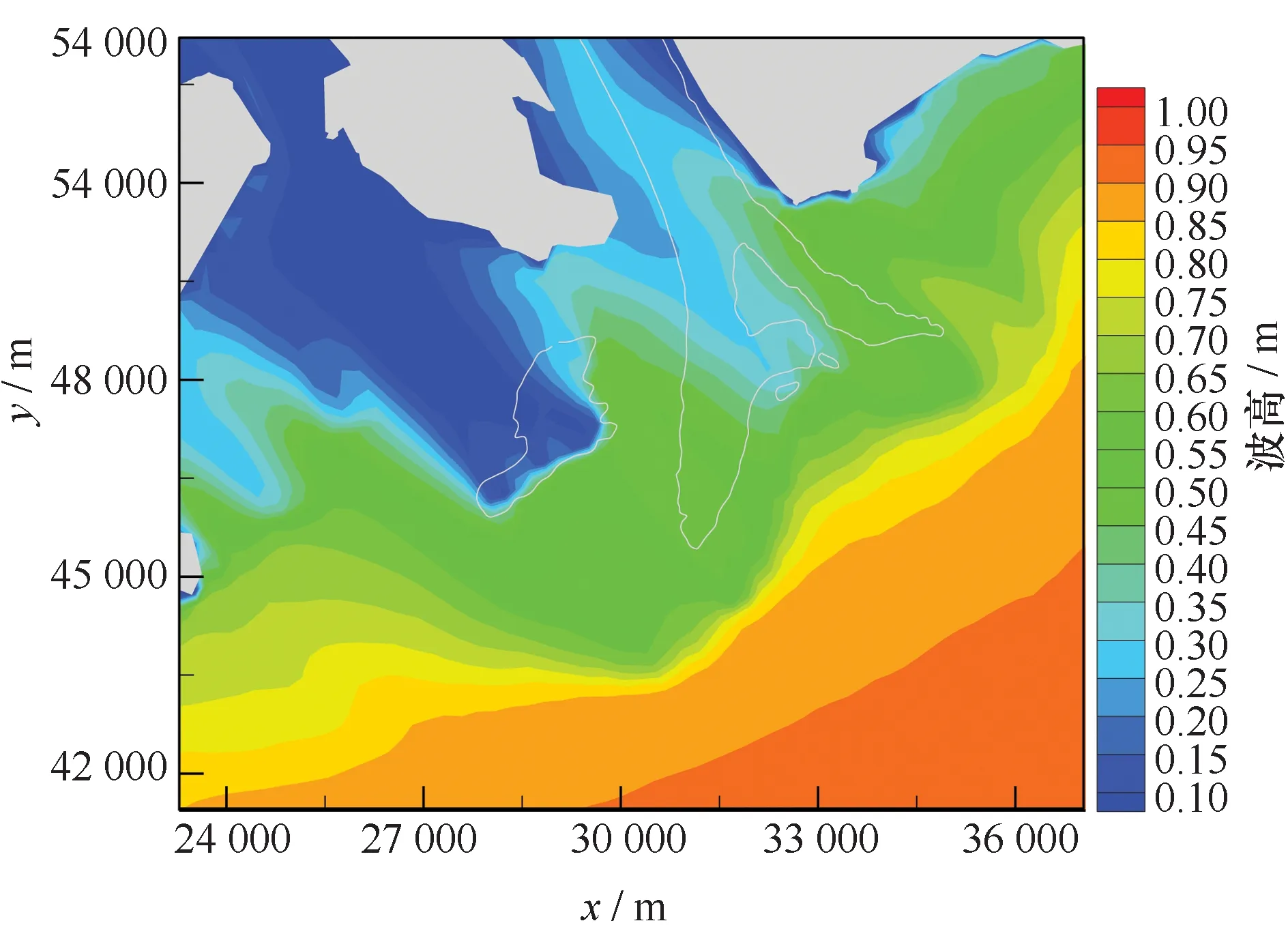
图6 磨刀门河口典型时刻的波高分布Fig.6 The wave height distribution of Modaomen estuary

枯季磨刀门外海平均波向为SE向，外边界处波高取1.01 m。大万山波浪站位于磨刀门口外东南侧27.9 km处，该处率定波高为0.99 m。九澳波浪站位于磨刀门口外东北侧14.6 km处，该处率定波高为0.52 m。枯季潮汐及上游径流边界以“2001.2”水文组合控制，该水文组合含大、中、小3个潮型，本文以 “中潮”为代表。模型通过启动和不启动波浪辐射应力项来代表“有浪”波生流工况和“无浪”纯潮流工况，同一时刻两者的异同反映了波浪的影响。

4.1 落潮阶段

落潮阶段，落急时刻“有浪”和“无浪”工况的流场差异最小，落憩时差异最大。图7给出的是“2001年2月”枯季水文组合落憩时刻的流场，背景彩色云图为河口地形高程分布；图7a为“无浪”工况潮流场，图7b是“有浪”工况的波流场。图8中的云图为“有浪”波生流流速与“无浪”潮流流速之差，背景流场为“有浪”工况的波流场。

图7 磨刀门枯季中潮落憩时刻“无浪”潮流场(a)和“有浪”波生流场(b)比较Fig.7 The comparison of the wave induced current flow field in the ebb slack tide between the tide-only (a) and wave-tide-united (b) simulations

图8 枯季中潮落憩(a)和落急(b)时“有浪”波流场及其与“无浪”潮流场的速度差分布情况Fig.8 The comparison of the numerical wave induced current flow field in the ebb slack tide (a) and maximum ebb tide (b)

综合图7和8，落憩时刻磨刀门河口区整体流速较小，波浪对潮流的影响显著。图7a中落憩时刻“无浪”工况潮流流态平顺，整体流向由东南向转向西南向。图7b中“有浪”工况，由于SE向波浪运动方向与落潮流向相反，浅滩流速以减小为主；横洲浅滩流速减小达-0.15 m/s；拦门沙沙脊东南侧浅滩形成两个旋转方向相异的主回流区，流速呈带状减小或者反向，减小值在-0.18 m/s左右；四沙东北侧流速顺波向反向偏转明显；三灶东侧浅滩也形成一个回流区。受波浪作用下各浅滩流速减小或反向的影响，磨刀门横洲主槽落潮流在拦门沙三角区上游端向东西两汊深槽集中，深槽内流速增大0.07 m/s左右；龙屎窟落潮流也向四沙和三灶之间水深相对较大的区域集中下泄，该区域流速增大达0.08 m/s。

落急时刻磨刀门河口区流速较大，“无浪”和“有浪”工况从流场整体上看差别不明显。从图8b中落急时刻的速度差分布可知，由于波浪运动方向与落潮流方向相反，磨刀门河口流速仍旧在浅滩以减小为主，在深槽增大。落急时流速减小最明显的区域为横琴南浅滩区(-0.13 m/s)，其次是横洲浅滩(-0.11 m/s)，再次是中心拦门沙浅滩(-0.07 m/s)、四沙波影区及三灶东侧浅滩区；流速增大区域主要为拦门沙东西两汊的深槽内(0.04 m/s)及四沙与三灶岛之间的深槽内。

4.2 涨潮阶段

涨潮阶段，图9给出的是“2001.2”枯季水文组合涨憩时刻的流场和地形分布；图9a为“无浪”工况潮流场，图9b是“有浪”工况波流场。图10给出的是“有浪”工况的波流场与“无浪”潮流场流速之差，背景为“有浪”工况的波流场，图10a为涨憩时刻，图10b为涨急时刻。

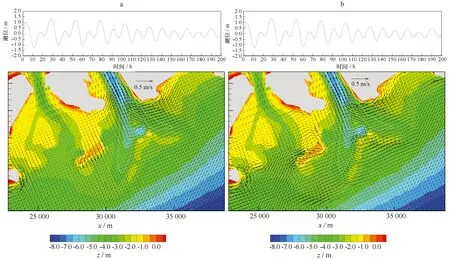
图9 磨刀门枯季中潮期涨憩时刻“无浪”潮流场(a)和“有浪”波生流场(b)比较Fig.9 The comparison of the wave induced current flow field in the flood slack tide between the tide-only (a) and wave-tide-united (b) simulations

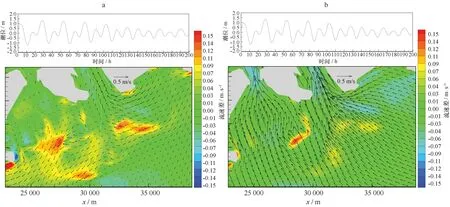
图10 枯季中潮涨憩(a)和涨急(b)时刻“有浪”波流场与“无浪”潮流场的速度变化分布情况Fig.10 The comparison of the numerical wave induced current flow field and the velocity changes in the flood slack tide (a) and maximum flood tide (b)

涨憩时刻(图9和图10)，“无浪”工况仅受潮位驱动，拦门沙以上区域为涨潮流，以下为落潮流，河口区流态平顺，无回流区。“有浪”时，波浪作用方向与潮流流向一致，加之该时刻磨刀门河口区潮流较弱，受波生流驱动，整个河口区出现大范围的流速增加，浅滩区域还出现顺浪向偏转和调整，比如拦门沙、四沙、横琴南、交杯沙及三灶西侧等浅滩区，拦门沙及四沙浅滩还由落潮流变成顺波向的冲越流。流速增幅最大的区域为拦门沙外坡浅水区和四沙，其次是三灶和横琴南浅滩区，再其次是四沙与三灶之间的深水区。受波生流影响，东汊深槽和横洲深槽西侧浅滩区流速减小。

涨急时刻(图10b)，“无浪”潮流场和“有浪”波流场差别较小，流场变化和“涨憩”时刻类似，受波浪作用影响，拦门沙浅滩流速增大值在0.07 m/s左右，四沙浅滩流速增大值在0.13 m/s左右。东汊深槽流速出现减小，减小值在-0.07 m/s左右。

4.3 计算成果合理性分析

本文建立的数学模型尽管经过了严格验证，但算例的复杂程度不及磨刀门河口，因此需分析成果合理性。磨刀门属径流-波浪型河口[29—30]，河口地貌是其主要动力因子长期作用的结果。从图5中河口地形可知，拦门沙沙脊处有双驼峰结构，拦门沙外坡内凹。从经典沉积地貌学分析，如果仅受径流和潮流作用，拦门沙不会形成双驼峰结构和外坡内凹形态。数值模拟表明，波浪在拦门沙浅滩区破碎后形成波生流，并于落潮时形成多个小范围回流区。相比“无浪”工况，“有浪”工况流速梯度分布变化较大，加之拦门沙区域以粉砂和粉细砂为主，流速梯度变化在落潮时减弱泥沙向海输运，涨潮时增大向陆输运，促进了泥沙在拦门沙区域的滞留和沉积，在两个主要回流区中心各形成一个驼峰，在拦门沙外坡形成利于波能耗散的内凹形态；该双驼峰和内凹外坡即是拦门沙区域以波浪作用为主的地貌演变结果。

另外文献[31]结合地形资料认为在波浪作用下，四沙浅滩为拦门沙向西北迁移形成。由图9b的波生流流场可知，考虑波浪作用后，拦门沙和四沙之间存在明显的水流通道，四沙则因波浪作用还出现顺浪向冲越流；而图9a不考虑波浪作用时，不仅不存在该水流通道，而且流向主要以落潮为主。根据以上3处地貌特点分析，间接表明本文波生流结果合理。

5 结论和展望

本文建立曲线坐标系下的双曲型缓坡方程，结合考虑波浪辐射应力的深度平均潮流数学模型，在采用Hamm实验[34]对模型进行验证之后，利用该模型首次研究了枯季磨刀门河口区的波生流流场及波浪对潮流场的影响。研究表明，枯季磨刀门河口区波生流明显，波浪对枯季磨刀门河口潮流影响较大。落潮时，波浪作用方向与潮流流向相反，波浪对潮流有顶托作用，拦门沙、横琴南及四沙等浅滩处流速均减小，拦门沙左右两汊的深槽内流速增大。涨潮时，波浪作用方向与潮流流向相同，波浪对潮流上溯有助涨作用，拦门沙、横琴南及四沙等浅滩处流速均有顺波向反向或增大，拦门沙左右两汊深槽内流速减小。

以往磨刀门河口动力研究以径流和潮流为主，未考虑波浪的影响。本文研究表明，枯季磨刀门河口波生流对拦门沙及河口浅滩区的潮流流场影响较大。磨刀门河口拦门沙形态有明显的波浪塑造特性。若不考虑波浪作用及波生流效果，将无法准确模拟磨刀门河口区的泥沙运动。因此未来本模型将扩展为磨刀门河口区的波浪潮流泥沙模型。

[1] Longuet-Higgins M S, Stewart R W. Radiation stress and mass transport in gravity waves, with application to surf-beats[J]. Journal of Fluid Mechanics, 1962, 13(4):481-504.

[2] 李孟国,张大错.浪致近岸水位变化及流场的数值计算[J].海洋学报, 1996, 18(4):96-113.

Li Mengguo，Zhang Dacuo. The numerical modeling of wave induced nearshore water level changes and flow field[J]. Haiyang Xuebao, 1996, 18(4): 96-113.

[3] Sun T, Tao J. Experimental and numerical study of wave-induced long-shore currents on a mild slope beach [J].China Ocean Engineering, 2005, 19(3): 469-484.

[4] 白志刚, 周锡礽. 波流耦合作用的缓坡方程数学模型研究[J]. 中国港湾建设, 2003(4):16-18, 26.

Bai Zhigang, Zhou Xireng. Numerical model study on mild-slope equation coupling wave with current[J]. China Harbour Engineering, 2003(4):16-18, 26.

[5] 王厚杰, 李瑞杰. 近岸区域波流耦合作用的数学模型[J]. 海洋湖沼通报, 1999(3): 1-9.

Wang Houjie, Li Ruijie. A coupling model for nearshore waves and wave induced currents[J]. Transaetions of Oceanology and Limnology, 1999 (3): 1-9.

[6] 佟飞飞, 沈永明, 崔雷. 基于曲线坐标系下缓坡方程模拟近岸波浪及波生流[J]. 中国科学: 物理学 力学 天文学, 2011, 41 (2): 161-169.

Tong Feifei, Shen Yongming, Cui Lei. Numerical simulation of nearshore waves and wave-induced currents based on mild-slope equation in curvilinear coordinates[J]. Scientia Sinica Phys, Mech & Astron, 2011, 41 (2): 161-169.

[7] 王世澎, 梁书秀, 孙昭晨. 二维情况下波浪对潮流场作用的数值分析[J]．海洋学报, 2007, 29(2): 174-178.

Wang Shipeng, Liang Shuxiu, Sun Zhaochen. The numerical analysis of wave effects on a tidal current in two dimensions[J]．Haiyang Xuebao, 2007, 29(2): 174-178.

[8] Wu X Z, Zhang Q H. A three-dimensional nearshore hydrodynamic model with depth-dependent radiation stresses[J]. China Ocean Engineering, 2009, 23(2): 291-302.

[9] 解鸣晓, 张玮. 近岸波生流运动三维数值模拟及验证[J]. 水科学进展, 2011, 22(3): 391-399.

Xie Mingxiao, Zhang Wei. 3D numerical modeling of nearshore wave-induced currents[J]. Advances in Water Science, 2011, 22(3): 391-399.

[10] Sun D T. Three-dimensional numerical modeling of nearshore circulation[J]. Acta Oceanologica Sinica, 2008, 27(S):101-118.

[11] 熊伟, 翟剑峰, 朱志夏, 等. 基于有限体积法的三维波生近岸流数值模型[J]. 水动力学研究与进展,A辑, 2016, 31(1): 43-49.

Xiong Wei, Zhai Jianfeng, Zhu Zhixia, et al. Three-dimensional nearshore current model based on finite volume method[J]. Chinese Journal of Hydrodynamics, 2016, 31(1): 43-49.

[12] 唐军, 沈永明, 郑永红, 等. 结合椭圆型缓坡方程模拟近岸波流场[J]. 海洋学报, 2006, 28(1): 146-151.

Tang Jun, Shen Yongming, Zheng Yonghong. The numerical simulation of nearshore current combined with the elliptic mild-slope equation[J]. Haiyang Xuebao, 2006, 28(1): 146-151.

[13] 唐军, 魏美芳. 非结构化网格下近岸波生流数值模拟[J]. 海洋学报, 2010, 32(6): 41-46.

Tang Jun, Wei Meifang. Numerical simulation of near-shore wave-induced currents on unstructured grid[J]. Haiyang Xuebao, 2010, 32(6): 41-46.

[14] Tang J, Shen Y M, Shi F, et al. Numerical study of wave and longshore current interaction[J]. Acta Oceanological Sinaca, 2012, 31(3): 10-17.

[15] 房克照, 邹志利, 刘忠波. 沙坝海岸上裂流的数值模拟[J]. 水动力学研究与进展, A辑, 2011, 26(4): 479-486.

Fang Kezhao, Zou Zhili, Liu Zhongbo. Numerical simulation of rip current generated on a barred beach[J]. Chinese Journal of Hydrodynamics, 2011, 26(4): 479-486.

[16] 荆海晓. 浅水非线性色散波模型的优化及在波生流问题中的应用[D]. 天津: 天津大学, 2014.

Jing Haixiao. Optimization of dispersive nonlinear shallow water wave model and its application to wave induced currents[D].Tianjin: Tianjin University, 2014.

[17] 李绍武, 黄筱云. 用Boussinesq方程计算沿岸流的数值方法[J]. 天津大学学报, 2004, 37(12): 1059-1062.

Li Shaowu, Huang Xiaoyun. Numerical method for calculation of longshore current by using boussinesq equations[J]. Journal of Tianjin University, 2004, 37(12): 1059-1062.

[18] 卢吉, 余锡平. 基于Boussinesq方程的近岸波流统一模型[J]. 水动力学研究与进展: A 辑, 2008, 23(3) : 314-320．

Lu Ji，Yu Xiping. Model for both nearshore waves and wave-induced currents based on Boussinesq equation[J]. Chinese Journal of Hydrodynamics, 2008, 23(3) : 314-320．

[19] 杨静思. 波流实时耦合模式的建立及应用[D]. 天津: 天津大学, 2012.

Yang Jingsi. Development and application of a dynamically coupled wave-current model[D]. Tianjin: Tianjin University, 2012.

[20] 赵张益, 张庆河. 基于间断有限元方法的三维近岸波生流数值模型建立[J].海洋工程,2014, 32(1):8-16.

Zhao Zhangyi，Zhang Qinghe. A numerical model of three-dimensional nearshore wave-induced currents based on discontinuous Galerkin method[J]. The Ocean Engineering, 2014, 32(1): 8-16.

[21] Zheng J H, Tang Y. Numerical simulation of spatial lag between wave breaking point and location of maximum wave-induced current[J]. China Ocean Engineering, 2009, 23(1): 59-71.

[22] Liang B C, Zhao H P. Numerical study of three-dimensional wave-induced longshore current's effects on sediment spreading of the Huanghe River mouth[J]. Acta Oceanologica Sinica, 2012, 31(2): 129-138.

[23] Xu Z, Zhang W. Wave-induced flow and its influence on ridge erosion and channel deposition in Lanshayang channel of radial sand ridges[J]. Journal of Hydrodynamics, 2014, 26(6): 882-893.

[24] 解鸣晓. 淤泥质海岸波生流动力机制及三维模拟研究[J]. 泥沙研究, 2012(6): 11-18.

Xie Mingxiao. Mechanism and three-dimensional numerical modelling of wave-induced currents on mudflats[J]. Journal of Sediment Research, 2012(6): 11-18.

[25] 王平, 张宁川. 非结构化网格下大范围波生流模拟和应用[J]. 海洋工程, 2013, 31(5): 45-54.

Wang Ping, Zhang Ningchuan. Numerical simulation of large-scale wave-induced current on unstructured meshes and its application[J]. The Ocean Engineering, 2013, 31(5): 45-54.

[26] Bennis A C, Ardhuin F. Comments on the depth-dependent current and wave interaction equations- A revision [J]. Journal of Physical Oceanography, 2011, 41(10): 2008-2012.

[27] 包四林, 西村仁嗣. 近岸波生流数值计算的一种新方法[J].海洋学报,2000,22(5):115-123.

Bao Silin, Hitoshi Nishimura. A new model for analyses of nearshore current[J]. Haiyang Xuebao, 2000, 22(5): 115-123.

[28] 包四林, 西村仁嗣, 陈沈良. 人工岛周围的波生流计算方法[J].海洋学报, 2010,32(6):41-46.

Bao Silin, Hitoshi Nishimura, Chen Shenliang. Method of calculating wave-induced current around artificial island[J]. Haiyang Xuebao, 2010,32(6):41-46.

[29] 王世俊. 珠江磨刀门河口研究现状与展望[J]. 人民长江, 2013, 44(21): 19-23.

Wang Shijun. Research status and prospect of Modaomen estuary of Pearl River[J]. Yangtze River, 2013, 44(21): 19-23.

[30] 李春初. 珠江河口咸潮问题之我见[J]. 热带地理, 2013, 33(4): 496-499.

Li Chunchu. My opinion on salt tide in the Pearl River Estuary[J]. Tropical Geography, 2013, 33(4): 496-499.

[31] 胡达, 李春初, 王世俊. 磨刀门河口拦门沙演变规律的研究[J]. 泥沙研究, 2005(4): 71-75.

Hu Da, Li Chunchu, Wang Shijun. Study on evolutional processes of the sand bar in Modaomen estuary[J]. Journal of Sediment Research, 2005(4): 71-75.

[32] Tong F F, Shen Y M, Tang J, et al. Numerical modeling of the hyperbolic mild-slope equation in curvilinear coordinates[J]. China Ocean Engineering, 2010, 24(4):585-596.

[33] Liu C, Deng J Q. Wave, tide and sediment transport modeling in the nandujiang estuary, Hainan, China[C]// Proceedings of the Fourth International Conference on Estuaries and Coasts. 2012.

[34] Hamm L. Directional nearshore wave propagation over a rip channel: an experiment[C]//Proceeding of the 23rd International Conference of Coastal Engineering, Venice, Italy. 1992: 226-239.

[35] Sørensen O R, Schäffer H A, Madsen P A. Surf zone dynamics simulated by a Boussinesq type model. III. Wave-induced horizontal nearshore circulations[J]. Coastal Engineering, 1998, 33: 155-176.

The numerical investigation of wave induced current in the dry season in the Modaomen estuary

Liu Cheng1，Liang Yan2，Peng Shi1， Hou Peng1

(1.PearlRiverHydraulicResearchInstitute,PearlRiverWaterResourcesCommissonoftheMinistryofWaterResources,Guangzhou510611,China; 2.CCCC-FHDIEngineeringCompanyLimited,Guangzhou510230,China)

A hyperbolic mild-slope equation wave propagation model was united with a depth-averaged 2D tidal flow model and the wave effect on flow is generated by radiation stresses of waves added to the tidal flow model. The wave induced current in the Modaomen estuary in the dry season was investigated for the first time by the model with the topography measured in 2011. The numerical results show that during the ebb tide the seaward currents are reduced by the opposing wave and two stagnant zones arise inside the shoaling water of the mouth bar, the seaward currents in east and west shoals also decrease, but the seaward currents inside the east and west deep grooves increase. During the flood tide the landward currents are increased by the following wave and a washover zone arise inside the mouth bar, the landward currents in east and west shoals also increase, but the landward currents inside the east and west deep grooves reduce at the same time.

Modaomen estuary; wave induced current; radiation stress; mild-slope equation; depth-averaged 2D tidal flow model

10.3969/j.issn.0253-4193.2017.01.001

2016-04-27；

2016-07-05。

广东省科技计划项目(2013B020200008)； 国家自然科学基金项目(50909110, 51579025)； 广东省自然科学基金项目(9151061101000001)； 国家重点基础研究发展计划项目(2013CB430403)。

刘诚(1975—), 男, 湖北省潜江市人, 高工, 博士, 主要从事河口海岸研究工作。E-mail:jacklc2004@163.com

P731.23

A

0253-4193(2017)01-0001-10

刘诚，梁燕，彭石, 等. 磨刀门河口枯季波生流场数值模拟研究[J]. 海洋学报, 2017, 39(1): 1-10,

Liu Cheng，Liang Yan，Peng Shi, et al. The numerical investigation of wave induced current in the dry season in the Modaomen estuary [J]. Haiyang Xuebao, 2017, 39(1): 1-10, doi:10.3969/j.issn.0253-4193.2017.01.001