海面风应力偏离风向的观测与分析

陈胜,乔方利,郭景松，焦志勇

(1.中国石油大学(华东) 理学院，山东 青岛 266580；2.国家海洋局第一海洋研究所 海洋环境与数值模拟研究室，山东 青岛 266061；3.青岛海洋科学与技术国家实验室 区域海洋动力学与数值模拟功能实验室，山东 青岛 266071)



海面风应力偏离风向的观测与分析

陈胜1, 2,乔方利2, 3*,郭景松2，焦志勇1

(1.中国石油大学(华东) 理学院，山东 青岛 266580；2.国家海洋局第一海洋研究所 海洋环境与数值模拟研究室，山东 青岛 266061；3.青岛海洋科学与技术国家实验室 区域海洋动力学与数值模拟功能实验室，山东 青岛 266071)

针对海气界面风应力方向与风向不一致的现象，2015年2月4日至3月12日在南海博贺观测平台开展了综合观测，利用涡动相关法计算了海气界面风应力，并在3类大气稳定度条件下分析了风应力矢量偏离风矢量的角度变化，进一步讨论了大气层结稳定时两者角度之差与风速的参数化关系。结果表明：在大气层结稳定条件下，风应力矢量偏向风矢量左侧，且偏离角度随逆波龄和风速增大而减小；当大气层结不稳定时，风应力矢量一般偏向风矢量右侧。海气界面风应力矢量受海表面风、波浪以及大气层结的共同调制。

涡动相关法；南海北部；海气边界层；大气层结；风应力矢量

1 引言

海气边界层之间的动量、热量和物质通量是描述大气边界层和海洋上表层相互作用的重要物理量，加深对海气通量的科学理解可为海洋环流、海浪甚至气候模式的发展提供科学支持。海气通量一直是海洋与大气科学领域的研究热点，在气候变化中具有重要地位。

海气界面的风应力(等价于动量通量)通常根据传统的块体公式估计，其大小正比于平均风速U的平方：

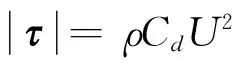
(1)

式中，ρ为空气密度，拖曳系数Cd是测量高度z、粗糙长度z0和层结的函数[1]。

海洋表面风应力的直接测量(涡动相关法)开始于20世纪70年代[1]。涡动相关法基于泰勒假设，将风速进行雷诺分解[2]，风应力矢量表达为：

τ=τx+τy=-ρ〈u′w′〉i-ρ〈v′w′〉j，

(2)

式中，u′,v′,w′分别代表水平x方向、y方向和垂直方向平均风速的脉动值。参照Grachev等的做法[3]，取τx=-ρ〈u′w′〉i=τxi为顺风向应力，τy=-ρ〈v′w′〉j=τyj为横风向应力，τx>0代表顺风向应力与风向一致，反之相反；τy>0代表横风向应力矢量在风矢量右侧，反之相反。

一般认为，〈v′w′〉项相对于〈u′w′〉项可以忽略[3]，〈v′w′〉≈0。但实际观测表明〈v′w′〉不为0，即风应力矢量会偏离风矢量[3]。风应力矢量和风矢量之间的夹角α可定义为：

α=arctan(〈v′w′〉/〈u′w′〉)，

(3)

式中，α为正(负)值代表风应力矢量指向风矢量右(左)侧(左手坐标系)。本文中风和波浪以及风应力方向的定义采用惯例，正北来向为0°，顺时针方向旋转为正值。

很多对海洋表面风应力的研究大多侧重在应力大小或其他标量(如拖曳系数、摩擦速度、粗糙长度等)[4—6]，但是风应力矢量方向经常不同于风矢量方向，两者存在夹角，该夹角有时很大甚至反向，导致应力大小也会发生改变。Geernaert[7]从Navier-Stokes方程出发，推导出风应力方向与风向之间的夹角最大不超过5°，然而最早由Smith[8]和Zemba和Freihe[9]观测结果显示，风应力与风向夹角比较大，甚至比Navier-Stokes方程预测的大1个量级，个别情况下超过了90°。Geernaert[7]利用北海两个站点不同观测高度(7.5 m和33 m)测得的海气动量通量数据，也发现风应力与风向存在明显夹角，并且将风与风应力间夹角30%的统计差异归因于海气界面热量通量。Geernaert等[1]进一步研究结果显示：在微风且海气热量通量近似为零情况下，风应力的方向很大程度上受表面波浪的影响，虽有此推断，但依据的数据仅有13组，数据非常有限。Rieder等[10]利用1990年3月在北太平洋表面波项目(Surface Waves Processes Program, SWAPP)中获得的资料，也注意到风应力和平均风矢量间有明显的夹角，发现风应力方向依赖于风向和长波的方向，与Geernaert等[1]推断的结果一致，且弥补了其原来数据有限的缺陷。Rieder和Smith[11]讨论了波浪对风应力的影响，通过剔除与波浪相关的应力，得到的剩余风应力与块体公式计算出的风应力符合较好。Grachev和Fairall[12]基于3次外海观测研究了微风(U<2 m/s)情况下海洋和大气之间的动量交换，发现海洋会向大气输送动量，表面风应力与涌浪方向相反；Grachev等[3]基于太平洋FLIP船的观测研究了风应力方向与风向以及表面波浪的关系，同样发现风应力方向与平均风向偏离较大，甚至反向。Bernardes和Dias[13]发现不稳定层结下，平均风矢量与风应力方向不一致，并且随着不稳定性增加，两矢量之间夹角会加大。虽然多数研究专注于改善动量通量大小的估计，但观测证据表明表面风应力矢量方向并不像传统Monin-Obukhov边界层相似理论刻画的仅简单受控于局地风向，其方向与大气层结紧密相关[7]；另外，大气常通量边界层的海洋表面水质点是运动的[14]，波浪运动会贡献部分应力，对风应力矢量特征影响较大。

以往研究表明风应力矢量与风矢量方向之间存在夹角，除Geernaert等[1]依托灯塔开展观测外，绝大部分观测研究是基于FLIP船基通量观测[3,10—12]。但固定平台的大量观测数据为定量研究风应力方向问题带来了新的契机。基于国家海洋局第一海洋研究所设计的波浪和海气通量综合观测系统对海气通量以及波浪参数进行直接测量，利用南海北部博贺固定观测平台于2015年2月4日至3月12日(共37 d)期间的观测数据，本文研究不同大气层结稳定度下，表面波浪以及风速对风应力方向的影响，并给出了稳定层结下风应力偏离风矢量的角度α与风速的参数化关系。

2 海上观测及数据处理

2.1 海上观测

中国气象局广州热带海洋气象研究所博贺海洋气象观测平台位于21°26.5′N，111°23.5′E(图1，以下简称海洋气象平台)，该平台位于广东省茂名市电白县莲头岭半岛中部东面约6.5 km处，平均水深约17 m，海洋气象观测平台距海面平均高度约为11 m[15]。考虑到距海面10 m高度处有一小的平台，通量观测误差可能较大。因此，国家海洋局第一海洋研究所设计的海气通量观测设备架设在平台上距平均海面约17 m处，朝向70°，设备包括三维超声风速仪、CO2/H2O红外气体分析仪、温度和湿度传感器、红外测温探头等，采样频率设置为10 Hz，通过数据采集箱连续采集高频数据。波浪观测采用NORTEK声学波浪流速剖面仪(AWAC，声波频率1 MHz)，距离博贺平台100 m，波浪测量平均时间间隔1 h，每小时以采样频率1 Hz工作1 024 s，获得波浪原始数据，经质量控制后得到有效波高、谱峰周期和平均波向等波浪参数。

2.2 数据处理

风应力估计采用1 h平均间隔[6]，为检验1 h平均时间是否足够长以至于捕获了所有通量，利用2月8日3：00—4：00的代表性的数据分成3:00—3:15、3:00—3:30、3:00—3:45和3:00—4:00，基于间隔分别为15 min、30 min、45 min、60 min的4段数据检查的频率累计曲线(Ogive曲线)，如图2所示。可以看出只有60 min的Ogive曲线在低频段接近于常值-0.062 m2/s2，不再随频率的减小而变化，而其他Ogive曲线在低频段变化较大，表明1 h作为平均时间尺度能满足各态历经假设[16]。在后期数据处理时，将原始数据分成一系列平均时间1 h的数据段，对每小时的数据段经过野点剔除、坐标旋转、线性去除趋势等[15,17]，得到1 h平均时间的通量数据。利用37 d的原始湍流和波浪数据，参照王介民[17]剔除野点过多时次数据的方法，经过计算处理，共获得856组数据。

图1 博贺海洋观测平台位置Fig.1 The location of Bohe Station

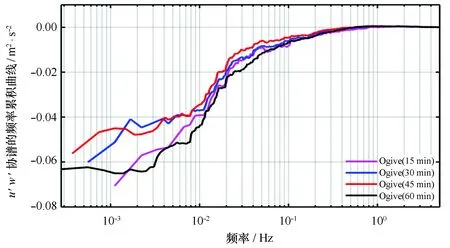
图2 u′w′协谱从高频到低频的频率累计曲线Fig.2 The cumulative sum of u′w′ co-spectra from high to low frequencies紫色-Ogive(15 min)，蓝色-Ogive(30 min)，红色-Ogive(45 min)，黑色-Ogive(60 min)Purple, blue, red and black line indicate Ogive 15 min, 30 min, 45 min and 60 min respectively

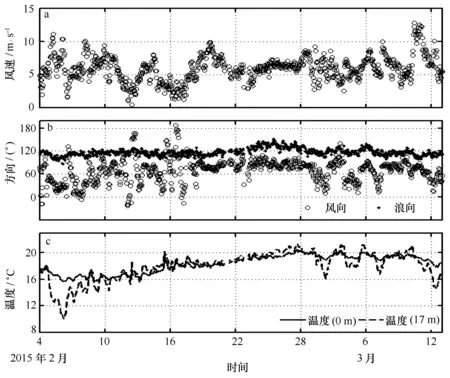
图3 风速(a)、风向与浪向(b)、海表皮温(实线)和距离海平面17 m处气温(虚线)(c)随时间变化图Fig.3 Time series of wind speed (a), wind and wave direction (b), and skin temperature of sea surface (solid line) and air temperature at 17 m (dash line) temperature (c)

图4 有效波高(a)、谱峰周期(b)和波龄(c)随时间变化图Fig.4 Time series of significant wave height (a), peak period (b), and wave age (c)

3 观测要素的基本特征

观测时段内的风速、风向和浪向，以及距离海平面17 m处和海洋皮温(0 m)温度的时间序列如图3所示，有效波高Hs、谱峰周期Tp以及波龄Cp/U17的时间序列如图4所示。整个观测期间风速一般在10 m/s以下，只有在2月6日和3月11日2天内风速出现少数10 m/s以上情况(图3a)，也就是说，风速基本处于中低风速情况。风向大部分时间小于90°且以东北风为主(图3b)，观测时段为典型海洋冬季，东北季风影响南海北部，但波向在115°附近，偏东南向；海表面温度在16～20℃之间(图3c)，而距离海平面17 m高度处气温在10～21℃之间，部分时段变化剧烈，海气温差变化直接影响大气层结。观测期间大部分时间有效波高在1 m以下，谱峰周期在5 s以上(图4a和b)，图4c中的细实线表示波龄Cp/U17=1.07[18]，波龄基本上在1.07以上，只有少数情况在1.07以下，由波浪参数以及图3b中风向与浪向对比可以看出，在整个观测时间段内，波浪以涌浪为主。

4 风应力矢量方向

参照王介民[17]对856组最终通量数据进行质量保证和质量控制获得479组可用于分析风应力矢量的高质量数据，Rieder等[10]结果显示，风速大于8 m/s时风应力与风矢量之间很小；Grachev和Fairall[12]结果表明，风速小于2 m/s情况下海洋会向大气输送动量。本文只对风速在2～8 m/s之间的数据进行统计分析，处理后的有效数据总共为380组。

利用Monin-Obukhov法[19]根据大气层结稳定度参数ζ=z/L(z为测量高度，L为Monin-Obukhov长度)将数据分为不稳定层结(ζ<-0.01)、中性层结(-0.01≤ζ≤0.01)[10]和稳定层结(ζ>0.01)3类数据，分别为80、13和287组。对筛选后的数据根据公式(3)求取风应力矢量与风矢量之间的夹角α，其时间序列如图5a所示。在整个时间段内，稳定层结居多，尤其在2月10日至3月1日期间，大气层结基本处于稳定状态。图3c显示在2月10日至3月1日期间，距海平面17 m处的气温与海表皮温相差较低，且前者要比后者温度略高，也表明此段时间大气层结稳定。而在2月4日至2月10日期间，海表皮温明显高于17 m处气温，表明该期间大气层结处于不稳定状态。而其他时间段，两者温度有高有低，大气层结变化不定，与图5a结果吻合。风应力与风矢量夹角与大气稳定度的线性相关性较弱(图5b)，在同一稳定度下，夹角也会受到波浪等因素的影响。不稳定层结条件下的风应力与风矢量夹角值较为分散，而稳定层结下风应力与风矢量夹角为负值(α<0)的数据约占95%，介于-40°到0°间的约占91%，较为集中，夹角平均值约为-20°，个别情况下达到了-80°(图5b)，应力矢量方向几乎与风向垂直[3]，α<0代表风应力矢量偏向风矢量左侧，与Geernaert等[1，7]提出的大气层结稳定时应力矢量偏向风矢量左侧一致。观测期间不稳定层结条件下夹角为正值(α>0)数据约占55%，最大值接近80°，半数以上符合大气层结不稳定时应力矢量偏向风矢量右侧的现象。因近中性与不稳定数据量较少，统计特征不明显，下面进一步分析稳定层结下，风应力矢量与风矢量夹角随风速、逆波龄等参数的关系。

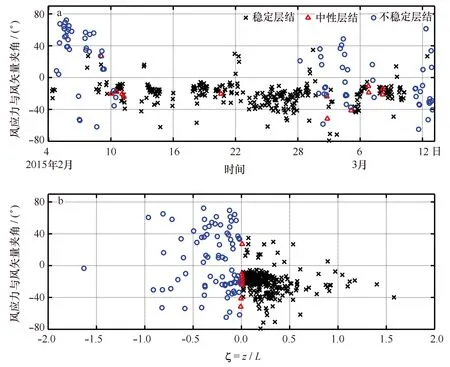
图5 不同层结下风应力与风矢量夹角(α)随时间变化图(a)和夹角(α)与大气稳定度关系图(b)Fig.5 Time series of angle (α) between wind and wind stress under 3 different stratifications (a), and the relationship between angle and stratification stability (b)

由以上分析可知，稳定大气层结数据占有效总数据的75%，在此情况下，风应力矢量与风矢量间之间的夹角α(只对夹角小于0的数据进行分析，该部分约占95%)对风速等参量作统计分析，夹角与风速、逆波龄之间的关系见图6。为给出夹角随风速的变化趋势，取0.5 m/s为平均子区间，对每个子区间内的夹角进行平均，并通过最小二乘法进行拟合得到夹角随风速变化的趋势线，可见，夹角绝对值随风速增大而减小，即风应力方向会随风速增大逐渐与风向趋于一致。当风速较低时，动量通量受海浪特别是涌浪的调制，涌浪方向可能与风向相差很大，从而导致风应力方向偏离风向；而当风速逐渐增大时，风浪开始起主导作用，而风浪一般是沿着风向的(二者之间有时也有一定夹角)，其诱导产生的应力也是沿风向的应力，故风应力方向会逐渐与风向保持一致。通过图中逆波龄与夹角的关系来看，风应力与风矢量夹角绝对值随着逆波龄的增大呈减小趋势，当海况较为成熟，即逆波龄较小时，海表面以涌浪为主，涌浪一般会偏离局地风向，涌浪会对风应力的调制使得风应力方向偏离风向；而当逆波龄较大时，海况为年轻，正在成长的状态，风浪占据主导，使得风应力方向逐渐与风向一致。

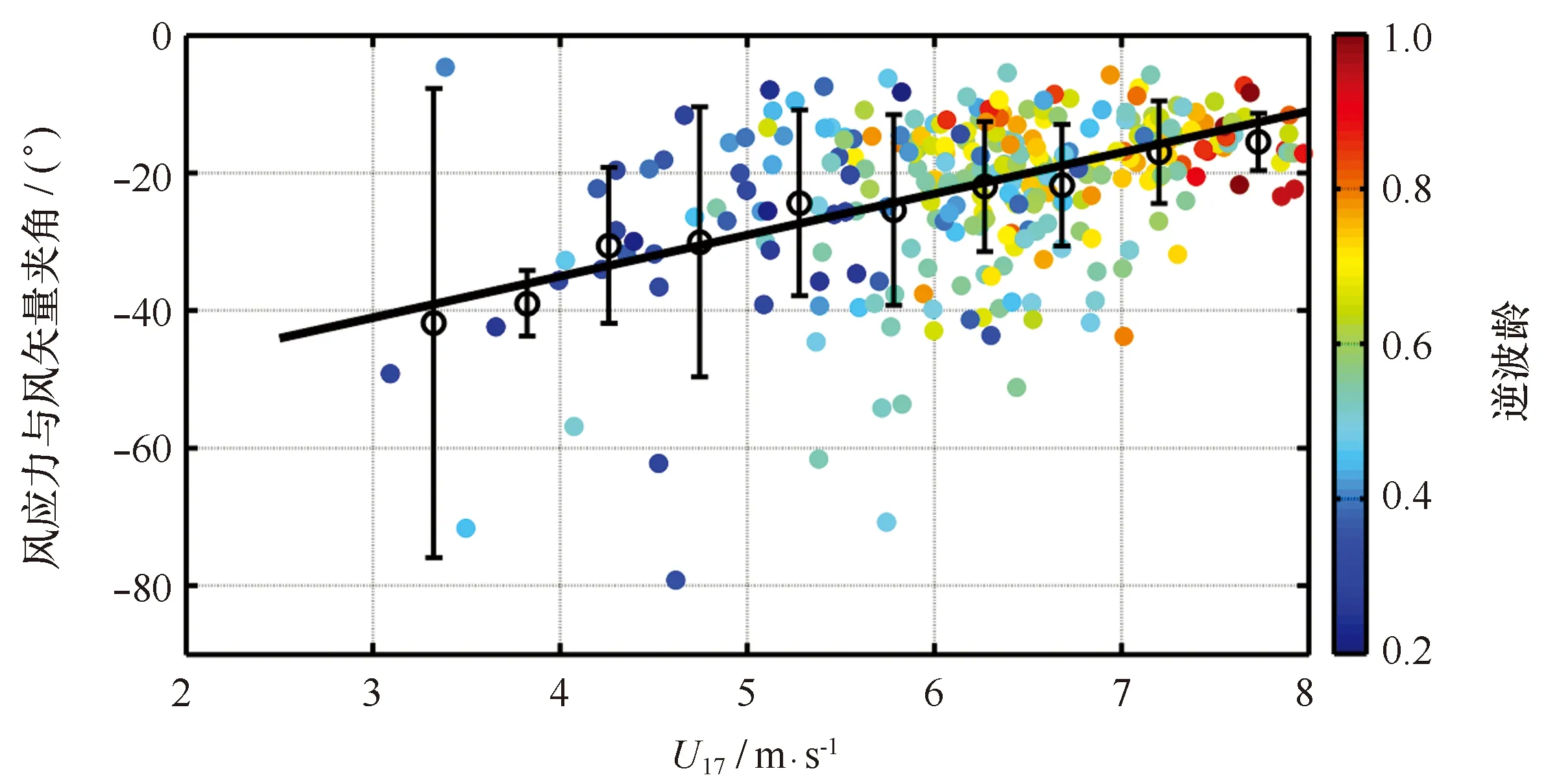
图6 稳定层结下风应力与风矢量夹角α与距海面17 m处风速U17、逆波龄U17cos θ/Cp的关系Fig.6 Stress off wind angle α vs 17 m wind speed U17 and inverse wave age U17cosθ/Cp under stable stratification

图6中，粗实线拟合线为α=6.6×U-62.6，其相关系数为96.7%，误差为-0.49°，能较好的拟合夹角随风速的变化关系，可以看出风应力矢量偏离风矢量的角度与风速拟合关系较好。但由于数据量仍较少，拟合线只能描述夹角随风速变化的趋势。在真实海洋环境条件下，风应力受大气层结的影响下，其大小和方向都会受到风以及波浪的共同调制，Ly[20]研究了风应力矢量与风矢量夹角对拖曳系数的影响，数值实验结果表明：在10°～20°的夹角会使得拖曳系数减小10%～20%。海浪影响在风应力估计中不可或缺。海气动量参数化方案需要改进，但需要更多的实测资料以及分析研究的支持。

5 结论

本文利用南海北部博贺固定平台的波浪与海气通量综合观测数据对风应力与风矢量偏角进行了分析与探讨，结果表明：

第一，在不同的大气层结状况下，风以及海浪的共同调制使得风应力方向会偏离风向。在稳定层结条件下，风应力向左偏离风向角度平均值约为20°，最大可达80°；在不稳定层结条件下，风应力偏离风向角度最大值接近80°，半数以上符合风应力矢量偏向风矢量右侧，向左偏离角度较小。

第二，在大气层结稳定情况下，风应力矢量偏离风向的角度与风速大小呈反比，与逆波龄也呈反比。风速越大，海洋越接近于风浪情况，导致风应力矢量与风矢量一致；逆波龄越大，即波龄越小，海洋越处于年轻或正在成长的海况，此时，风速一般较大，风应力矢量会与风矢量较为接近。

作用于海洋表面的风应力对多种物理过程产生直接影响，向下的动量通量(风应力)能够产生波浪、表面流、海气边界湍流等，然而在微风(U<2 m/s)条件下，局地涌浪会反作用于大气，产生向上的动量通量。风应力与风矢量的夹角会直接影响风应力的大小，要想准确定量分析海气动量通量，需要考虑波浪的影响。风应力从本质上讲是张量，而到目前为止所有的风应力参数化计算均是基于矢量。从本质上改进海气动量通量的表达，尚需大量实测、分析以及理论研究工作的支持。

[1] Geernaert G L, Hansen F, Courtney M, et al. Directional attributes of the ocean surface wind stress vector[J]. Journal of Geophysical Research: Oceans (1978—2012), 1993, 98(C9): 16571-16582.

[2] 黄艳松. 基于浮标观测资料的海气通量计算方法研究[D]. 青岛：中国科学院海洋研究所, 2011.

Huang Yansong. Estimation of air-sea fluxes from a buoy observation[D]. Qingdao: Institute of Oceanology, Chinese Academy of Science,2011.

[3] Grachev A A, Fairall C W, Hare J E, et al. Wind stress vector over ocean waves[J]. Journal of Physical Oceanography, 2003, 33(11): 2408-2429.

[4] Zhao D. A note on wave state dependence of sea-surface roughness[C]//The Twelfth International Offshore and Polar Engineering Conference. International Society of Offshore and Polar Engineers, 2002.

[5] Guan C, Xie L. On the linear parameterization of drag coefficient over sea surface[J]. Journal of Physical Oceanography, 2004, 34(12): 2847-2851.

[6] 邹仲水, 赵栋梁, 黄健, 等．海-气界面动量通量的估计方法分析与应用[J]. 海洋学报, 2014, 36(9): 75-83.

Zou Zhongshui, Zhao Dongliang, Huang Jian, et al. The analysis and application of estimation methods for air-sea interface momentum flux[J]. Haiyang Xuebao, 2014, 36(9):75-83.

[7] Geernaert G L. Measurements of the angle between the wind vector and wind stress vector in the surface layer over the North Sea[J]. Journal of Geophysical Research: Oceans (1978—2012), 1988, 93(C7): 8215-8220.

[8] Smith S D. Wind stress and heat flux over the ocean in gale force winds[J]. Journal of Physical Oceanography, 1980, 10(5): 709-726.

[9] Zemba J, Friehe C A. The marine atmospheric boundary layer jet in the Coastal Ocean Dynamics Experiment[J]. Journal of Geophysical Research: Oceans (1978—2012), 1987, 92(C2): 1489-1496.

[10] Rieder K F, Smith J A, Weller R A. Observed directional characteristics of the wind, wind stress, and surface waves on the open ocean[J]. Journal of Geophysical Research: Oceans (1978—2012), 1994, 99(C11): 22589-22596.

[11] Rieder K F, Smith J A. Removing wave effects from the wind stress vector[J]. Journal of Geophysical Research: Oceans (1978—2012), 1998, 103(C1): 1363-1374.

[12] Grachev A A, Fairall C W. Upward momentum transfer in the marine boundary layer[J]. Journal of Physical Oceanography, 2001, 31(7): 1698-1711.

[13] Bernardes M, Dias N L. The alignment of the mean wind and stress vectors in the unstable surface layer[J]. Boundary-Layer Meteorology, 2010, 134(1): 41-59.

[14] Smith S D, Fairall C W, Geernaert G L, et al. Air-sea fluxes: 25 years of progress[J]. Boundary-Layer Meteorology, 1996, 78(3/4): 247-290.

[15] 赵中阔, 廖菲, 刘春霞, 等．近岸海洋气象平台涡动相关数据处理与质量控制[J]．地球科学进展，2011,26(9):954-964.

Zhao Zhongkuo, Liao Fei, Liu Chunxia, et al. Processing and quality control of eddy covariance measurements from a coastal marine meteorological platform[J]. Advances in Earth Science, 2011,26(9):954-964.

[16] Friehe C A, Shaw W J, Rogers D P, et al. Air-sea fluxes and surface layer turbulence around a sea surface temperature front[J]. Journal of Geophysical Research: Oceans (1978—2012), 1991, 96(C5): 8593-8609.

[17] 王介民. 涡动相关通量观测指导手册(Ver. 20120212)[OL]. http://westdc.westgis.ac.cn/water/surveystd.2012.

Wang Jiemin. The instruction manual of the eddy flux observation(Ver. 20120212)[OL]. http://westdc.westgis.ac.cn/water/surveystd. 2012.

[18] 汪炳祥, 常瑞芳, 王一飞. 风浪与涌浪的划分判据[J]. 黄渤海海洋, 1990, 8(1): 16-24.

Wang Bingxiang, Chang Ruifang, Wang Yifei. Criteria of differentiating swell from wind waves[J]. Journal of Oceanography of Huang Hai & Bohai Gulfs, 1990, 8(1): 16-24.

[19] 毕雪岩, 刘烽, 吴兑. 几种大气稳定度分类标准计算方法的比较分析[J]. 热带气象学报, 2005, 21(4): 402-409.

Bi Xueyan, Liu Feng, Wu Dui. Comparision of some limit for stability classification[J]. Journal of Tropical Meteorology, 2005, 21(4): 402-409.

[20] Ly L N. Effect of the angle between wind stress and wind velocity vectors on the aerodynamic drag coefficient at the air-sea interface[J]. Journal of Physical Oceanography, 1993, 23(1): 159-163.

The observation and analysis on the deviation of wind stress direction from wind direction

Chen Sheng1, Qiao Fangli2,3, Guo Jingsong2, Jiao Zhiyong1

(1.CollegeofScience，ChinaUniversityofPetroleum,Qingdao266580,China; 2.LaboratoryofMarineEnvironmentandNumericalSimulation，FirstInstituteofOceanography,StateOceanicAdministration,Qingdao266061,China; 3.LaboratoryforRegionalOceanographyandNumericalModeling,QingdaoNationalLaboratoryforMarineScienceandTechnology,Qingdao266071,China)

Focusing on the inconsistent phenomenon between wind stress direction and wind direction on the air-sea interface, we designed comprehensive observation at the Bohe Station of the South China Sea from February 4 to March 12, 2015. The wind stress was calculated by using the eddy correlation method, the deviation angle between the wind stress and wind vector was analyzed under 3 different atmospheric stability conditions. Furthermore, the parametric relationship between the angle and wind speed was proposed under the stable atmospheric stability condition. Results showed that the stress vector is to the left of the wind for the air stable condition, besides, the deviation angle decreases with the increase of inverse wave age and wind speed, while the stress vector is generally to the right of the wind for the unstable case. The wind stress vector depends on not only the sea surface winds, but also on the surface waves and atmospheric stable conditions.

eddy correlation method; northern South China Sea; air-sea boundary layer; atmospheric stability; wind stress vector

10.3969/j.issn.0253-4193.2017.01.003

2015-11-15；

2016-05-22。

国家自然科学基金委员会——山东省人民政府联合资助海洋科学研究中心项目(U1406404)；鳌山科技创新计划研究项目(2015ASKJ01)。

陈胜(1989—)，男，山东省商河县人，博士研究生，主要从事海气界面湍流通量研究。E-mail：Rain@fio.org.cn

*通信作者：乔方利(1966—)，男，山东省庆云县人，研究员，主要从事海洋环流数值模拟、海洋与气候变化、海洋与气候数据分析方法与应用等研究。E-mail：qiaofl@fio.org.cn

P731.2

A

0253-4193(2017)01-0028-08

陈胜, 乔方利, 郭景松, 等. 海面风应力偏离风向的观测与分析[J]. 海洋学报, 2017, 39(1): 28-35,

Chen Sheng, Qiao Fangli, Guo Jingsong, et al. The observation and analysis on the deviation of wind stress direction from wind direction[J]. Haiyang Xuebao, 2017, 39(1): 28-35, doi: 10.3969/j.issn.0253-4193.2017.01.003