某混合斜拉桥曲塔预应力钢束空间张拉顺序分析

王 震

（1.中交第一公路勘察设计研究院有限公司，陕西 西安 710075；2.长安大学， 陕西 西安 710064）

某混合斜拉桥曲塔预应力钢束空间张拉顺序分析

王 震

（1.中交第一公路勘察设计研究院有限公司，陕西 西安 710075；2.长安大学， 陕西 西安 710064）

为确定施工阶段曲塔的预应力钢束空间张拉顺序，确保曲塔在预应力张拉阶段的受力合理，以某混合斜拉桥的曲塔为工程背景，详细介绍了该桥曲塔的构造和预应力布置的特点，计算了桥塔关键截面的预应力配筋率，并与预应力混凝土箱梁0号块的配筋率进行了对比，采用有限元分析软件Midas FEA分析了预应力钢束空间张拉顺序的不同对桥塔的力学特点的影响，并给出了优化后的张拉顺序。

曲塔；预应力钢束；张拉顺序；预应力布置；有限元分析；优化

随着城市建设的发展，满足城市景观的考量，出现了很多新型的桥梁结构形式，同时也带来了很多新的技术难题。例如，近年来出现的空间曲塔，主塔空间曲线的新颖造形会导致其受到弯拉剪扭联合作用，构造和受力复杂，整体双向弯曲及扭转效应非常明显，混凝土容易开裂，同时也给主塔的施工带来了很多问题［1］。例如：主塔采用分节段施工，节段拼装难度较大，需要严格控制施工过程的主塔变形；混凝土浇筑、振捣过程中因局部受力过大产生的鼓包，需要严格控制混凝土浇筑高度并从安全角度考虑在结构内部设置拉筋；尤其是节段预应力钢束空间张拉顺序不当会导致主塔局部混凝土主拉应力过大有开裂的风险，导致桥塔受力不利，需要进行分析确定合理的预应力钢束空间张拉顺序［2-4］，而目前广泛采用的杆系模型不能计算出结构细部的应力水平，不能够详细地得出预应力钢束张拉后桥塔节段的应力变化，难以模拟其空间受力状态，特别是对预应力钢束的模拟［5-6］。本文结合某混合斜拉桥的曲塔预应力钢束张拉方案采用Midas FEA建立了实体模型对桥塔的预应力钢束空间张拉顺序进行了分析，为同类型结构的施工制定科学合理的钢束空间张拉顺序提供借鉴和参考。

1 工程概况

某混合斜拉桥为塔梁墩固结体系的无背索曲塔曲梁斜拉桥，主桥平面位于半径为800 m的圆曲线上，主桥跨径布置为（51.5+138+55）m，主桥布置如图1所示。

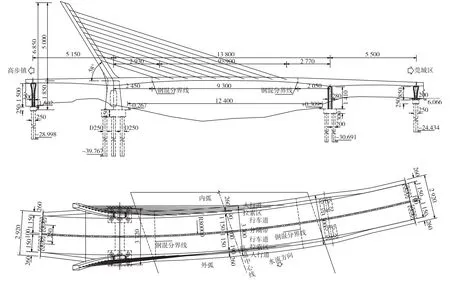
图1 主桥布置图（单位：cm）

该桥首先将主墩与主墩处箱梁以及主塔1号节段一起进行施工，再进行主桥其他节段箱梁的施工，待主桥合龙后，安装主桥桥面吊机，吊装主塔各个钢箱梁节段并灌注混凝土，直至桥塔施工完成。具体施工顺序如图2所示。

2 曲塔构造与预应力布置

主桥桥塔高50 m，顺桥向水平倾角为58°，倾向岸侧，横桥向往外圆弧张开，两个桥塔中心横向间距由塔梁结合位置的28.5 m变化到塔顶的40.9 m，为空间曲线形斜塔，桥塔被分隔成5个箱室，为矩形空心钢壳混凝土结构。

主塔顺桥向倾斜会导致主塔倾斜侧受拉，通过斜拉索张拉消除并增大轴力，横桥向弯矩通过在桥塔两侧设置塔内预应力以消除横向弯矩并增大轴力。塔上预应力分节段张拉，一端通过齿板锚固在下塔柱，另一端在相应节段完成后锚固在桥塔节段分界处，曲塔预应力布置如图3所示。

图2 主桥施工示意图（单位：cm）

由于主桥位于半径800 m的圆曲线上，索塔下游塔柱位于圆曲线外侧，受力较不利，故选取下游外曲线侧曲塔第一根拉索下的截面对其预应力配筋率进行计算，并与跨径一致的预应力混凝土箱梁0号块的配筋率进行对比。选取截面位置如图4所示，截面布置如图5所示。

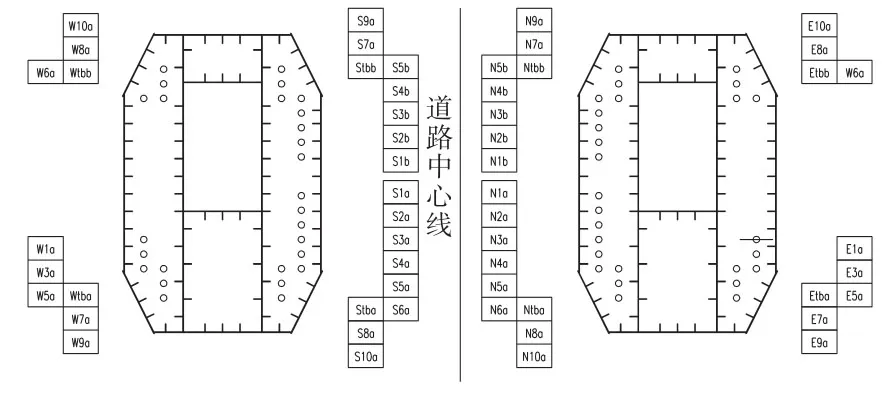
图3 曲塔预应力布置图（单位：cm）

图4 桥塔选取截面

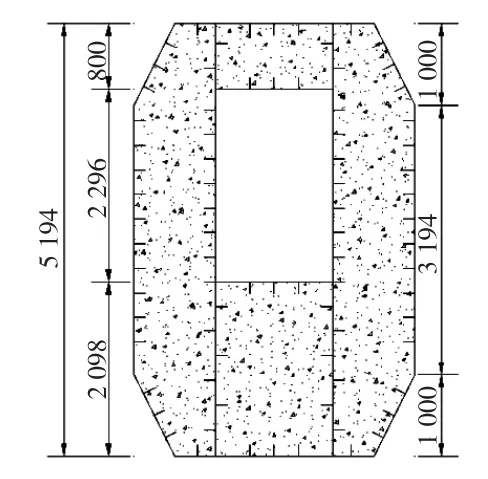
图5 选取截面布置（单位：cm）

根据该截面的预应力布置情况，计算得出了该截面的预应力配筋率，如表1所示。

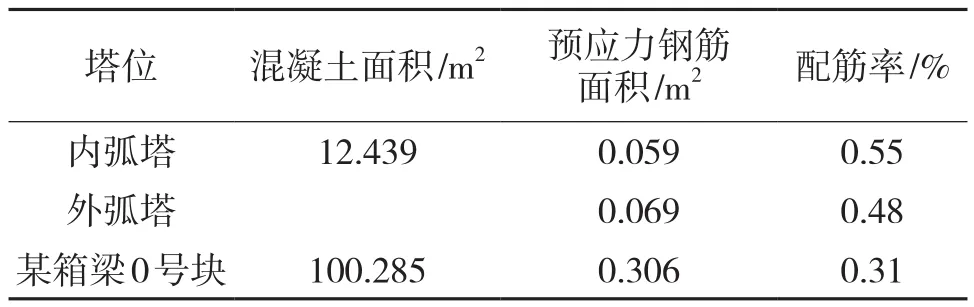
表1 选取截面预应力配筋率

从表1可以看出，该桥塔预应力配筋率较高，属于矩形空心钢壳预应力混凝土结构。

3 桥塔预应力张拉顺序分析

3.1 模型建立

主塔分为13个节段，前3节段施工完成后张拉第一批预应力，4节段～12节段为各节段施工完成后张拉该节段的预应力，13节段未布置预应力。本文对桥塔各个阶段预应力的张拉顺序进行了分析，选取了外弧塔前3个节段进行了第一批预应力张拉顺序研究，选取节段如图6所示，预应力钢筋布置如图7所示。

采用Midas FEA建立有限元实体模型，桥塔混凝土采用四节点四面体单元，桥塔钢壳及加劲肋采用四节点板单元，不考虑加劲肋开孔影响。程序自动考虑钢筋与混凝土耦合，钢壳、加劲肋与混凝土共节点，混凝土采用C50，钢材采用Q345，均按照规范取值。有限元模型如图8所示。

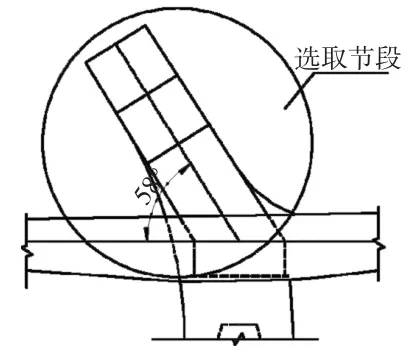
图6 选取外弧塔节段示意图

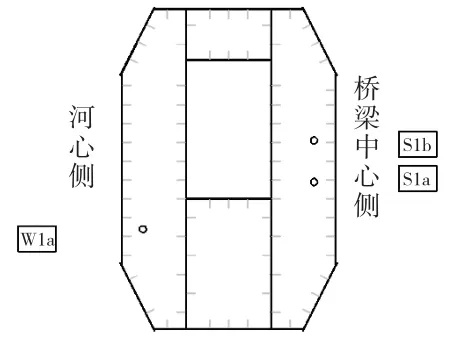
图7 张拉预应力布置图

图8 有限元模型图

将外弧塔3节段施工过程中的预应力张拉过程划分为6个张拉顺序，如表3所示，按照各顺序进行施工阶段分析。

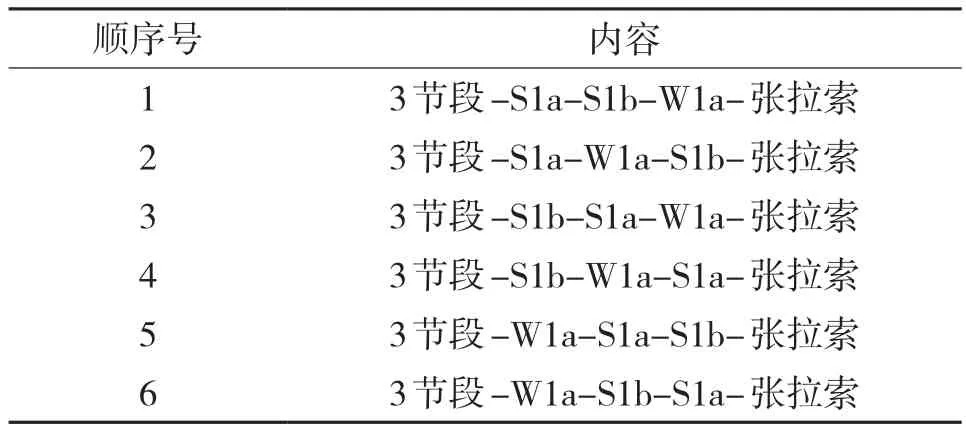
表3 预应力张拉顺序

3.2 应力分析

按照顺序1进行预应力钢束张拉，提取主要工况下的轴向应力云图，如图9所示。

同理对其他的张拉顺序进行分析，提取各顺序下的计算结果，得出各预应力钢束张拉后混凝土轴向应力的变化范围，如表4所示。

从表4可以看出，顺序5相对于其他顺序表现出整个张拉过程中结构有更大的压应力储备，且整个张拉过程中节段的最大拉应力均比其他顺序低。

3.3 应力变化对比

从力学角度分析，桥塔因受拉可能开裂的部位出现在曲线外沿侧，即桥塔的桥梁中心线侧与河心侧，故选取该方向塔底1截面的两个测点，提取曲塔前3节段各顺序下的应力值，对比其应力变化情况，选取截面如图10所示，截面测点如图11所示。

3.3.1 河心侧应力变化

如图12所示，桥塔1截面河心侧整体受拉，最大拉应力出现在3节段浇筑后，为1.5 MPa，此阶段可能导致裂缝的产生，随着预应力的张拉，结构应力逐渐减小，斜拉索张拉后河心侧达到同一应力水平，处于受压状态，图形中最靠下部的曲线说明该顺序为预应力钢束张拉阶段结构的压应力水平最大，故从下往上进行排序，顺序如下：

图9 S1a-S1b-W1a混凝土应力云图

表4 各顺序下轴向应力计算结果 MPa

3.3.2 桥梁中心侧应力变化

如图13所示，桥塔1截面桥梁中心侧整体受压，随着预应力的张拉，顺序5、顺序6应力先增大后减小，其他顺序应力先减小后增大，斜拉索张拉后应力增大，达到同一应力水平，按照相同的原则进行排序如下：

S1b-S1a-W1a＞S1a-S1b-W1a＞S1b-W1a-S1a＞S1a-W1a-S1b＞W1a-S1b-S1a＞W1a-S1a-S1b。

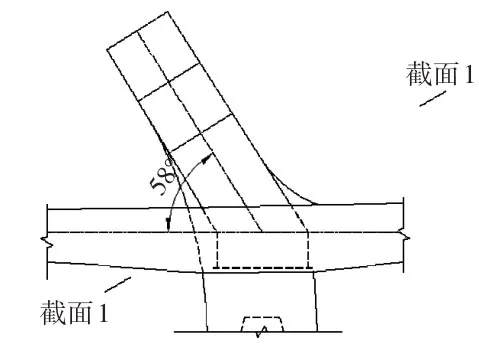
图10 选取截面示意图

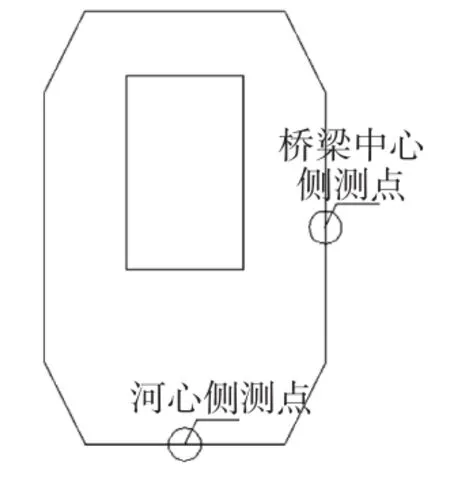
图11 截面测点示意图

图12 河心侧混凝土轴向应力变化图

图13 桥梁中心侧混凝土轴向应力变化图

3.4 优化预应力张拉顺序

从以上分析得出：在桥塔节段浇筑完成后，河心侧混凝土裂缝产生的概率更大，故在预应力张拉进行过程中首先控制河心侧受力，再控制桥梁中心侧受力，故得出了预应力张拉过程按照桥塔河心侧为主控制侧，桥梁中心侧为辅控制侧的原则，桥塔前3节段预应力张拉顺序建议以顺序5进行，即W1a-S1a-S1b的张拉顺序，能够确保结构有更大的压应力储备。

按照相同的思路对其他节段预应力张拉进行分析，得出了桥塔各节段预应力张拉顺序如表5所示。

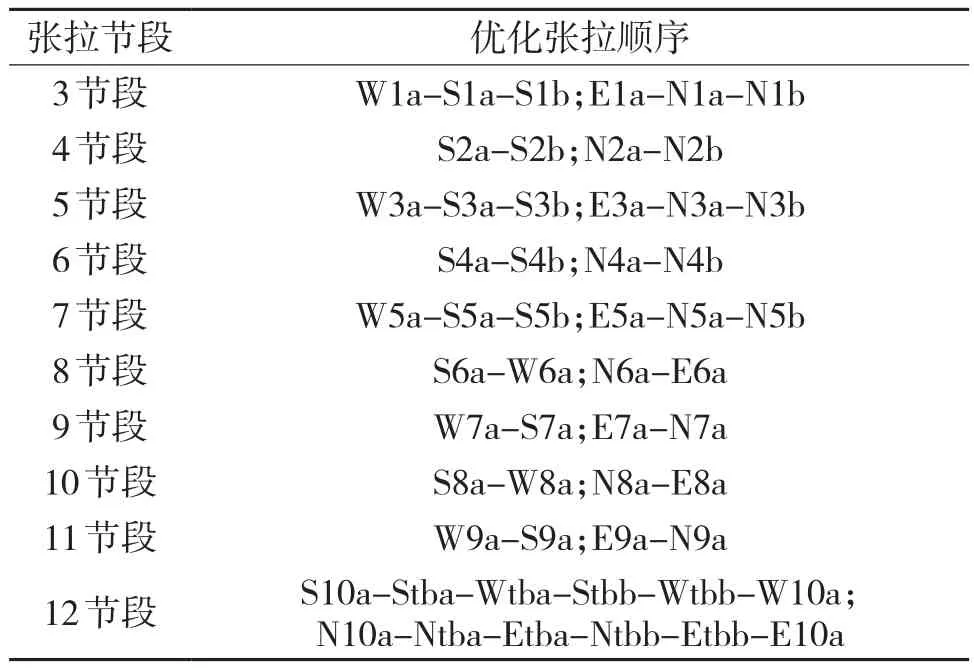
表5 优化的预应力张拉顺序表

根据计算得出的预应力钢束空间张拉顺序能够更好地保证桥塔在施工过程中的压应力储备，确保桥塔在施工过程中结构受力合理。

4 结语

本文分析了曲塔的空间受力特点以及施工中出现的新问题，针对曲塔预应力钢束空间张拉顺序不当可能导致混凝土开裂的问题进行了分析，以某混合斜拉桥曲塔为工程背景，介绍了其构造与预应力布置，计算了桥塔关键截面的预应力配筋率，并与两座预应力箱梁0号块的参数进行了对比，明确了主塔设计特点。采用有限元分析软件Midas FEA分析了不同的预应力钢束空间张拉顺序下桥塔的受力情况，并给出了优化的张拉顺序，为今后类似的新型结构的预应力张拉顺序研究提供了借鉴。

［1］ 琚明杰.无背索曲塔曲梁斜拉桥受力性能研究［D］.西安：长安大学，2009.

［2］盛捷.无背索曲塔曲梁斜拉桥力学性能分析与试验研究［D］.长沙：湖南大学，2012.

［3］杨敏.无背索曲塔曲梁斜拉桥的力学性能分析与研究［D］.广州：广东工业大学，2012.

［4］冷文华.预应力钢壳混凝土桥塔受力分析［D］.长沙：湖南大学，2012.

［5］孙东利，周莉，谢斌. 斜拉桥钢塔塔墩锚固设计与分析［J］.中外公路，2012，32（6）：192-195.

［6］刘世明，刘永健，耿东升，等.现浇箱梁预应力钢筋张拉方式影响分析［J］.公路交通科技，2013，30（3）：84-88.

Tension Analysis of Prestressed Steel Beam of Curved Pylons of A Hybrid Cable-stayed Bridge

Wang Zhen
（1. CCCC First Highway Consulants Co.,Ltd., Xi'an 710075, China; 2.Chang'an University, Xi'an 710064, China）

In order to confirm the optimized prestress tension sequence of the curved pylon and ensure the reasonable structure stress at prestressed tendons in tensioning, according to the curved pylons of a hybrid cable-stayed bridge, this paper introduced the structure and the arrangement of prestressed tendons of pylons in detail. The prestress radio of pylons were calculated and compared to the prestress beam's. By using the finite element model of midas fea, it analyzed the structure stress behavior in different construction stages of prestress tension sequence of curved pylons, and put forward the optimized prestress tension sequence.

curved pylons; prestressed tendons; tension sequence; arrangement of prestressed tendons; finite element analysis; optimized

U443.38

A

1672-9889（2016）06-0039-04

2016-01-08）

王震（1989-），男，陕西西安人，助理工程师，主要从事桥梁设计工作。