Comparisons Between the Ramanujan Constant and Beta Function
2017-01-18,,
, ,
(School of Sciences, Zhejiang Sci-Tech University, Hangzhou 310018, China)
Comparisons Between the Ramanujan Constant and Beta Function
QIUSongliang,LIQingqing,WANGXiaoyu
(School of Sciences, Zhejiang Sci-Tech University, Hangzhou 310018, China)
In this paper, the authors show the monotonicity and convexity properties of certain combinations defined in terms of the Ramanujan constantR(a)=-2γ-ψ(a)-ψ(1-a) and beta function B(a)=B(a,1-a)=π/sin(πa), and obtain asymptotically sharp lower and upper bounds forR(a)-B(a). Thus, they deeply reveal the relationship betweenR(a) and B(a,1-a) and improve some known results forR(a).
Ramanujan constant; psi and beta functions; monotonicity; convexity; lower and upper bounds
0 Introduction and Main Results
For x,y>0, the gamma, beta and psi functions are defined as
(1)
respectively. For their basic properties, the reader is referred to [1-4]. Here we only record following formulas applied frequently in the sequel, (cf. [1, 6.3.5, 6.3.7, 6.3.16, 6.4.10, 6.3.22 & 6.1.17], respectively):
ψ(1-x)-ψ(x)=πcot(πx),
(2)
(3)
(4)
(5)
The so-called Ramanujan constant R(a) is defined by
R(a)≡-2γ-ψ(a)-ψ(1-a).
(6)
for a∈(0,1), whereγ=0.5772156649…is the Euler constant. By the symmetry, we can assume that a∈(0,1/2] in (6). It is well known that R(a) is essential not only in the study of the generalized elliptic integrals and the theory of Ramanujan’s modular equations, but also in some other fields of mathematics such as quasiconformal theory. (See [1-3 & 5-11].) Some authors have obtained various analytic properties and functional inequalities for this function. (Cf. [3, 5 & 8-13].) On the other hand, the functions R(a) and
B(a)≡B(a,1-a)=Γ(a)Γ(1-a)=π/sin(πa)
(7)
often simultaneously appear in the related studies, and we have to reveal the relations between R(a) and B(a).
The main purpose of this paper is to show the monotonicity and convexity properties of certain combinations defined in terms of R(a),B(a) and some elementary functions, and to obtain asymptotically sharp lower and upper bounds for R(a)-B(a).By these results, several comparisons between R(a) and B(a) are presented, and some known related results are improved.
Throughout this paper, we let


Theorem 1 a) The function f(x)≡R(x)/B(x) is strictly decreasing from (0,1/2] onto[α,1). However, f is neither convex nor concave on (0,1/2].
b) For c∈(0,∞), let g(x)=R(x)-cB(x). Then g is strictly decreasing on (0,1/2] if and only if c≤1, and g is convex on (0,1/2] if and only if c≤1, with g((0,1/2])=[log16-cπ,∞)if c<1, and g((0,1/2])=[-β/2,0)if c=1. Moreover, for c∈(0,1] and n∈N,g(2n)is strictly decreasing and convex on (0,1/2], while g(2n-1)is strictly increasing and concave on (0,1/2]. However, if 1 c) If c=α, then the function h(x)≡g(x)/(1-2x)2is strictly decreasing and convex from (0,1/2) onto ([7ζ(3)-π2log2]/2,∞). In particular, for x∈(0,1/2], (8) with equality if and only if x=1/2. Theorem 2 a) The function F(x)≡[B(x)-R(x)]/x is strictly decreasing and convex from (0,1/2] onto [β,δ). In particular, for x∈(0,1/2], B(x)-βx-ηx(1-2x)≤R(x)≤B(x)-βx (9) with equality in each instance if and only if x=1/2. Furthermore, the derivative F′ is strictly increasing and concave from (0,1/2] onto (-2ζ(3),-2β]. (10) with equality in each instance if and only if x=1/2. In this section, we prove Theorem 1 stated in Section 0. a) Set y=x(1-x). It follows from (3) and (6) that (11) This yields the monotonicity of f. Next, differentiation gives πf″(x)=[R″(x)-π2R(x)+2πR′(x)cot(πx)]sin(πx). (12) By (3) and (6), we have R(x)=-2γ-ψ(1-x)-ψ(1+x)+(1/x), (13) R′(x)=ψ′(1-x)-ψ′(1+x)-(1/x2), (14) R″(x)=-ψ″(1-x)-ψ″(1+x)+(2/x3). (15) By (12), (16) and hence it follows from (13)-(15) that On the other hand, it follows from (12) that f″(1/2)=4[7ζ(3)-π2log2]/π=2.0032…>0. Hence f′ is not monotone on (0,1/2], so that f is neither convex nor concave on (0,1/2]. By (5), R(x) and B(x) can be rewritten as (17) (18) respectively, and hence (19) If c≤1, then by (19), g is strictly decreasing on (0,1/2]. If c>1, then so that g is not decreasing on (0,1/2], since (20) by (3).Thus, g is strictly decreasing on (0,1/2] if and only if c≤1. If c<1, then g(1/2)=log16-cπ, and If c=1, then g(1/2)=log16-π=-β/2, and g(0+)=0 by (19). If c≤1, then by (19), g′ is strictly increasing on (0,1/2] so that g is convex on (0,1/2]. On the other hand, by(20), (21) so that for c>1, and hence g is not convex on (0,1/2] if c>1. Consequently, g is convex(0,1/2] if and only if c≤1. The assertion for g(n)follows from the following expression If 1 g′(0+)=+∞,g′(1/2)=0,g″(0+)=-∞,g″(1/2)=28ζ(3)-cπ3>0. This shows that there exist x1and x2such that g′(x)>0 for 0 c) Differentiation and (19) give (22) where h1(x)=(1-2x)g′(x)+4g(x) and h2(x)=(1-2x)3.Clearly, h1′(x)=2g′(x)+(1-2x)g″(x), h1″(x)=(1-2x)g‴(x),g(1/2)=0 for c=α, and g′(1/2)=0 since Hence h1(1/2)=h2(1/2)=h1′(1/2)=h2′(1/2)=0.Since h1″(x)/h2″(x)=g‴(x)/24 (23) The inequality (8) and its equality case are clear. (24) which is strictly increasing on (0,1/2]. This shows that F′ is strictly increasing on (0,1/2] by [3, Theorem 1.25], and hence the convexity of F follows. The double inequality (9) and its equality case are clear. By (19), (25) (26) (27) where F3(x)=F4(x)/F5(x),F4(x)=2(1+t)+2x(tx-t1-x)logt-2(tx+t1-x)-x2(tx+t1-x)(logt)2and F5(x)=x3. Clearly, F4(0)=F5(0)=0. Differentiation gives F4′(x)/F5′(x)=[(tx-t1-x)(logt)2log(1/t)]/3, which is strictly decreasing in x on (0,1/2]. By[3, Theorem 1.25], this shows that F3is strictly decreasing in x on (0,1/2], and hence the concavity of F′ follows from (27). Clearly, F′(1/2)=F1(1/2)/F2(1/2)=-2β. Since sin3(πx)=π3[x3-(π2/2)x5+O(x7)]and cos2(πx)=1-(πx)2+O(x4)as x→0, it follows from (24) and (21) that b) Clearly, G(x) can be rewritten as (28) It is well known that for |t|<π, (29) (See [1, 4.3.68 & 23.1.18].) Hence (30) by (7), and it follows from (28) and (30) that (31) By part(1), F′ is strictly increasing on (0,1/2]. Therefore, (31) shows that G′ is strictly increasing on (0,1/2], and hence the convexity of G follows. By part (1) and the first equality in (31), we obtain the value G′(1/2)=-4β[1-(2/π)]<0. Hence G′(x)<0 for all x∈(0,1/2]by the monotonicity of G′. This yields the monotonicity of G. Clearly,G(1/2)=A1. By part(1), (28) and (30),G(0+)=A2. The double inequality(10) and its equality case are clear. Remark It is easy to verify that the lower (upper) bound given in (9) is greater than the lower (upper, respectively) bound given in (10). The lower (upper) bound given in (9) ((10), respectively) improves those of R(x) contained in [11, Theorem 2.3]. Theorem 1(a) improves [12, Theorem 2(1)] and [13, Theorem 2(4)] where there was no conclusion on the convexity and/or concavity for the function f(x)=R(x)/B(x)=[R(x)sin(πx)]/π, and (8) improves [12, (7)]. [1]ABRAMOWITZ M, STEGUN I A. Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Tables[M]. New York, Dover,1965:253-294. [2]QIU S L, VUORINEN M. Handbook of Complex Analysis:Special Function in Geometric Function Theory[M]. Elsevier B V,2005:621-659. [3]ANDERSON G D, VAMANAMURTHY M K, VUORINEN M. Conformal Invariants, Inequalities, and Quasiconformal Maps[M]. New York, John Wiley & Sons,1997:32-47. [4]QIU S L, VUORINEN M. Some properties of the gamma and psi functions with applications [J]. Math of Comput,2005,74:723-742. [5]ANDERSON G D, BARNARD R W, RICHARDS K C, et al. Inequalities for zero-balanced hypergeometric functions[J]. Trans Amer Math Soc,1995,347:1713-1723. [6]BALASUBRAMANIAN R, PONNUSAMY S, VUORINEN M. Functional inequalities for quotients of hypergeometric functions[J]. J Math Anal Appl,1998,218:256-268. [7]PONNUSAMY S, VUORINEN M. Asymptotic expansions and inequalities for hypergeometric function[J]. Mathematika,1997,44:278-301. [8]QIU S L, VUORINEN M. Infinite products and the normalized quotients of hypergeometric function[J]. SIAM J Math Anal,1999,30:1057-1075. [9]QIU S L. Singular values, quasiconformal maps and the Schottky upper bound[J]. Science in China (Ser. A),1998,41(12):1241-1247. [10]QIU S L. Grötzsch ring and Ramanujan’s modular equations[J]. Acta Math Sinica,2000,43(2):283-290. [11]WANG M K, CHU Y M, QIU S L.Sharp bounds for generalized elliptic integrals of the first kind[J]. J Math Anal Appl,2015,429:744-757. [12]QIU S L, FENG B P. Some properties of the Ramanujan constant[J]. J of Hangzhou Dianzi Univ,2007,27(3):88-91. [13]ZHOU P G, QIU S L, TU G Y, et al. Some properties of the Ramanujan constant[J]. J of Zhejiang Sci-Tech Univ,2010,27(5):835-841. (责任编辑: 康 锋) Ramanujan常数与Beta函数的比较 裘松良,李晴晴,王晓宇 (浙江理工大学理学院,杭州 310018) 给出了由Ramanujan 常数R(a)=-2γ-ψ(a)-ψ(1-a)和Beta函数B(a,1-a)=π/sin(πa)定义的一些组合的单调性与凹凸性,获得了R(a)-B(a,1-a)的一些渐近精确的上下界,从而深入揭示了函数R(a)与B(a,1-a)的大小关系,并改进了R(a)的一些已知的相关结论。 Ramanujan常数;psi和beta函数;单调性;凹凸性;上下界 10.3969/j.issn.1673-3851.2017.01.018 O156.4 Document code: A Article ID: 1673- 3851 (2017) 01- 0110- 06 Received date: 2016-04-24 Published Online: 2016-12-09 Fund item: This research is supported by the National Natural Science Foundation of China (NSFC) (1171307) Introdu ction of the first anthor: QIU Songliang (1957-), male, Fuyang, professor, research interests: complex analysis, quasiconformal theoery, special functions, Ramanujan’s moduar equations.
1 Proof of Theorem 1
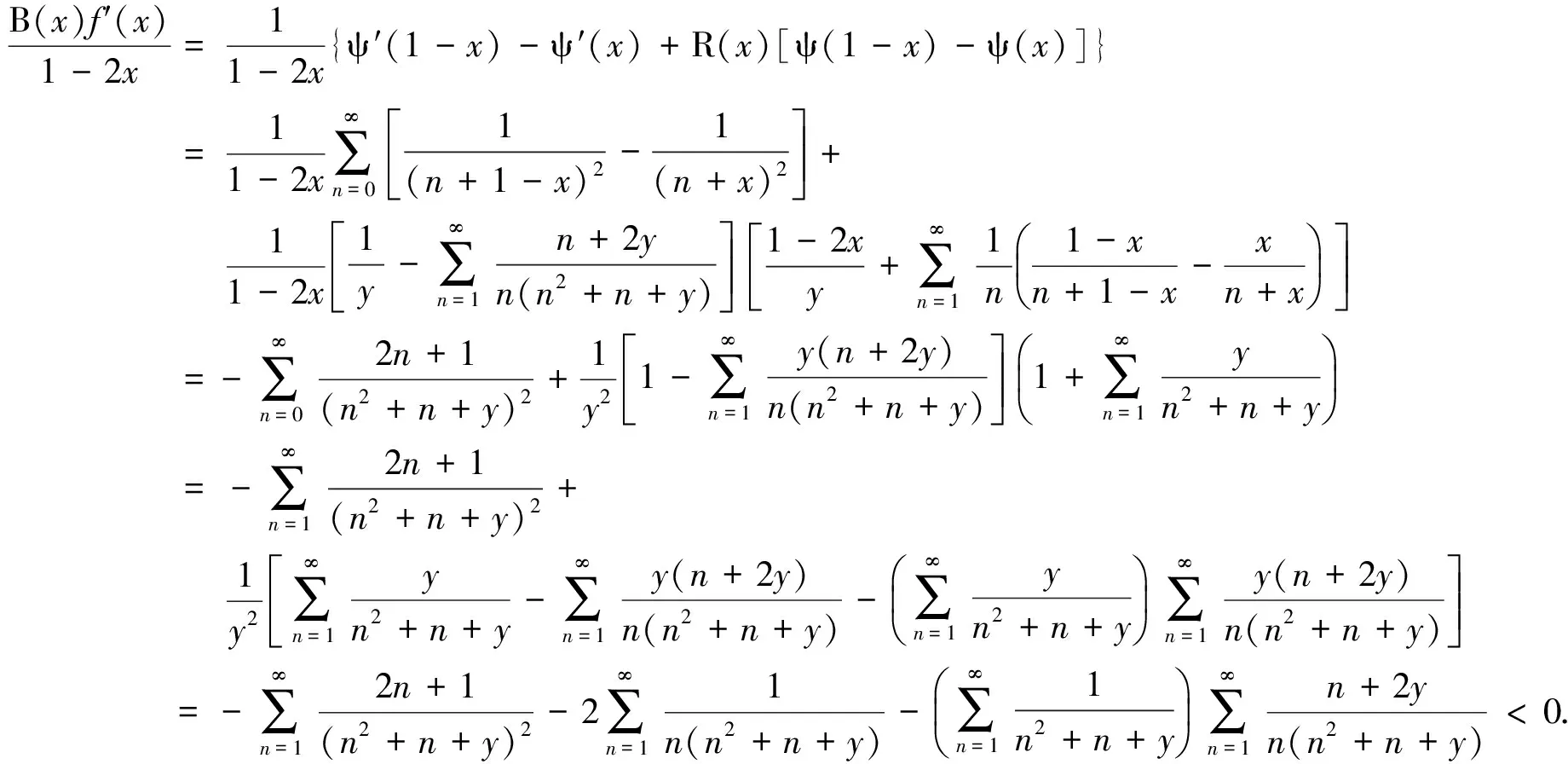
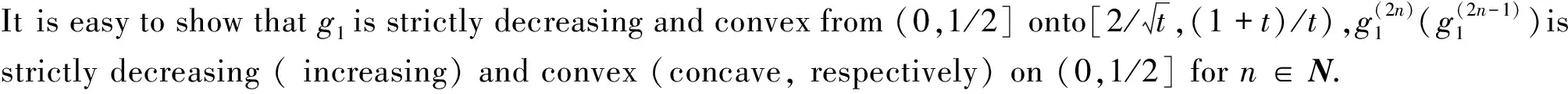
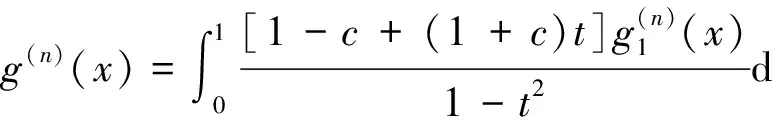

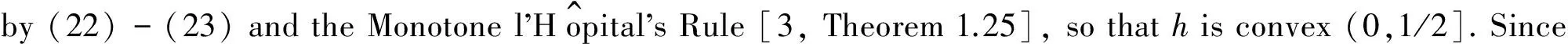

2 Proof of Theorem 2

