北斗空时抗干扰降维算法研究
2017-01-18张新帅吴雅娟陈金令
康 博,张新帅,路 明,吴雅娟,陈金令
(四川九洲电器集团有限公司,绵阳 621000)
北斗空时抗干扰降维算法研究
康 博,张新帅,路 明,吴雅娟,陈金令
(四川九洲电器集团有限公司,绵阳 621000)
空时抗干扰算法有着优良的抗干扰性能,但需要对高维矩阵求逆,计算量过大难以工程实现。因此,需要对其进行降低计算量处理以利于工程实现。基于相关相减多级维纳滤波法可降低计算量,并有着优良的抗干扰性能,对其进行了仿真试验,并证明了其有效性。
北斗系统;降维;相关-相减多级维纳滤波
0 引 言
随着我国北斗卫星导航系统的不断完善,其应用也越来越广泛,重要性也日益加深。但卫星信号自发射端到地面传输距离极远,到达地面的卫星信号功率很低,容易受到干扰的影响,致使接收机不能正常工作,不能提供有效的定位信息,因此需要在接收机前端增加抗干扰模块进行干扰抑制。目前主要的抗干扰方法有时域滤波抗干扰技术、空域滤波抗干扰技术、空时抗干扰技术和空频抗干扰技术等[1-2]。空时抗干扰技术是在空域抗干扰技术的基础上,在天线阵的每个阵子后面增加若干时间延迟单元,使得算法的自由度极大提高,能够更加有效地对窄带干扰和宽带干扰进行有效的抑制,使后端的接收机能够正常工作[3]。虽然空时抗干扰技术对干扰有着很好的抑制性能,但由于增加了若干延迟单元,使得自相关矩阵维度急剧升高,对自相关矩阵直接求逆的计算量很大,不便于工程实现,因此需要对其进行降维处理,降低计算量[4]。
J.S.Goldstein在维纳滤波的基础上做出了改进,提出了多级维纳滤波法(MWF)[5-6]。该方法每过一级维纳滤波自相关矩阵维度减1,而且该方法不用求解逆矩阵,但每级维纳滤波都含有一个阻塞矩阵,阻塞矩阵计算繁琐,经过MWF之后虽然计算量得到降低,但依旧较大[7]。在MWF基础上改进的相关相减多级维纳滤波法(CSA-MWF)避免了自相关矩阵和阻塞矩阵的求解,使得计算量得到进一步的简化。本文针对MWF和CSA-MWF进行了仿真实验,证明了相关相减多级维纳滤波法的有效性。
1 空时抗干扰技术
空时抗干扰技术在前端和空域抗干扰技术相同,都是若干个天线阵子按照一定的排列组成的天线阵,在每个天线阵子后面空时抗干扰技术增加了若干个时间延迟单元,进而形成了空时结构,其结构如图1所示。

图1 空时二维处理结构图
图1中M表示天线阵子的个数,N表示延迟单元的个数,Δ表示每个抽头的时延,Δ≤1/B,B表示信号的带宽,xij表示第i个天线阵子第j个抽头接收到底数据,wij表示第i个天线阵子第j个抽头的权值。
整个天线阵列的MN×1维接收数据向量X表示为:
(1)
权值矢量W可表示如下:
(2)
根据最小方差无失真响应准则(MVDR)可得:
(3)
最优全矢量可以表示为:
(4)

空时抗干扰算法的最终输出表示为:
(5)
2 多级维纳滤波法
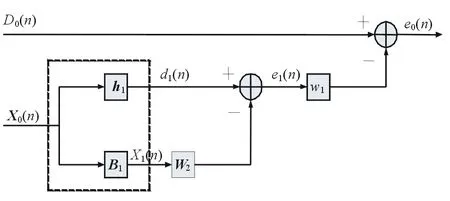
图2 二级维纳滤波结构图
在图2中,虚线框内为满秩矩阵T1:
(6)
式中:h1为d0与X0的归一化互相关向量,表示为:
(7)
B1为h1的阻塞矩阵,即:
B1h1=0
(8)
输入信号经过满秩矩阵T1得到A1(n),可表示为:
(9)
此时的权矢量表示为:
(10)
式中:
(11)
对其矩阵求逆得到:
(12)
式中:
(13)
因此:
(14)
式中:δ1=‖rX0d0‖。


图3 多级维纳滤波图
此刻,矩阵求逆转换为多个标量求倒数,计算量大大降低[8]。
在实际中,只需进行到D(D 相关相减多级维纳滤波法避免了多级维纳滤波法阻塞矩阵不易求出的问题,其结构框图如图4所示。 图4 CSA-MWF结构图 前向迭代部分: hi= Xi(n)=Xi-1(n)-hi(n)di(n) end 后向迭代部分: eD(n)=dD(n) end 权矢量迭代部分: wp=1 Wi=wp end 4.1 CSA-MWF抗干扰性能仿真 仿真条件:天线阵阵子个数M=7;延迟单元N=8;B1频点的入射信号信噪比-20 dB;分别从俯仰角50°、6°和-30°入射宽带、部分宽带和窄带3个干扰信号,干信比均为80 dB;其中宽带干扰信号的归一化频率为0~1;部分宽带干扰信号的归一化频率为0~0.5;窄带干扰信号的归一化频率为0.8;CSA-MWF阶数D=18;仿真结果如图5所示。 图5 CSA-MWF方向图 从仿真结果可以看出:在俯仰角50°方向上形成了归一化频率0~1、幅度约104dB的零陷,有效抑制了宽带干扰;在俯仰角6°方向上形成了归一化频率0~0.5、幅度约106dB的零陷,有效抑制了部分宽带干扰;在俯仰角-30°方向上形成了归一化频率0.8、幅度约105dB的零陷,有效抑制了窄带干扰,并且其它方向上方向图相对平坦,不会对其它方向入射的卫星信号进行抑制。因此可知,经过相关相减多级维纳滤波法后能够针对宽带干扰、部分宽带干扰和窄带干扰进行有效抑制,并且保留有效信号。 4.2 MWF和CSA-MWF输出均方误差对比 天线阵阵子个数M=3;延迟单元N=5;B1频点的入射信号信噪比-20dB;分别入射干信比均为80dB的窄带干扰信号、宽带干扰信号和混合干扰信号情况下不同滤波器阶数的MWF和CSA-MWF输出的最小均方误差如图6~8所示。 图6 宽带干扰情况下的最小均方误差 图7 窄带干扰情况下的最小均方误差 图8 混合干扰情况下的最小均方误差 从仿真结果可以看出:分别在宽带干扰、窄带干扰和混合干扰情况下,当滤波器阶数分别为6,2,7时,MWF和CSA-MWF同时收敛且输出的最小均方误差基本相同。因此CSA-MWF和MWF经过一定的滤波器阶数达到收敛时,两者的性能基本相同,但由于CSA-MWF不需要求解阻塞矩阵,计算量相对于MWF更低。 空时抗干扰技术虽然相对于传统的抗干扰技术有着更优秀的性能,但整个算法过程的计算量过大,给工程实现带来了不便,因此对其进行计算量简化的研究就十分必要。本文给出了相关相减多级维纳滤波法的算法过程,其不用求解阻塞矩阵和接收信号自相关矩阵求逆的特点使得该算法计算量相对于多级维纳滤降维算法的计算量更低,其性能基本相同,便于工程实现。 [1] 郭艺.GPS接收机空时抗干扰理论与实现关键技术研究[D].长沙:国防科技大学,2007. [2] 何訸.GNSS接收机抗干扰技术研究 [D].成都:电子科技大学,2013. [3] 董李梅.一种变步长自适应算法在GPS空时抗干扰中的应用[J].通信技术,2015,48(3):295-297. [4] 张海亮.导航接收机天线互耦校正及抗干扰算法研究 [D].成都:电子科技大学,2013. [5]SCOTTGJ,REEDIS,SCHARFLL.Amulti-stagerepresentationoftheWienerfilterbasedonorthogonalprojections[J].IEEE,1998, 44 (7):2943-2959. [6] 丁前军,王永良,张永顺.自适应阵列中多级维纳滤波器的有效实现方法[J].电子与信息学,2006,28(5):937-938. [7] 曹建波.GPS接收机降维空时联合处理算法研究 [J].现代导航,2014(3):162-163. [8] 杨克元.GPS接收机抗干扰算法及其实现研究 [D].成都:电子科技大学,2010. Study of Dimension Reduction Algorithm for Beidou Space-time anti-jamming KANG Bo,ZHANG Xin-shuai,LU Ming,WU Ya-juan,CHEN Jin-ling (Sichuan Jiuzhou Electric Group Co. Ltd.,Mianyang 621000,China) Space-time anti-jamming algorithm has good anti-jamming performance,but need perform matrix inversion to high-dimension matrix,so the engineering realization is difficult for large calculation quantity,thereby it is necessary for engineering realization to reduce the calculation quantity.Because the algorithm of correlation subtraction architecture of the multistage Wiener filter (CSA-MWF) can reduce the calculation quantity,and has fine anti-jamming performance,this paper performs simulation test and proves the validity. Beidou system;dimension reduction;correlation subtraction architecture of the multistage Wiener filter 2016-02-20 TN973.3 A CN32-1413(2016)06-0073-04 10.16426/j.cnki.jcdzdk.2016.06.0163 相关相减多级维纳滤波法

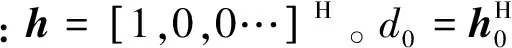
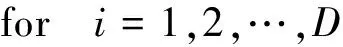
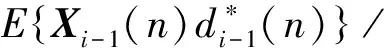

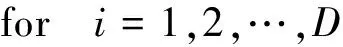
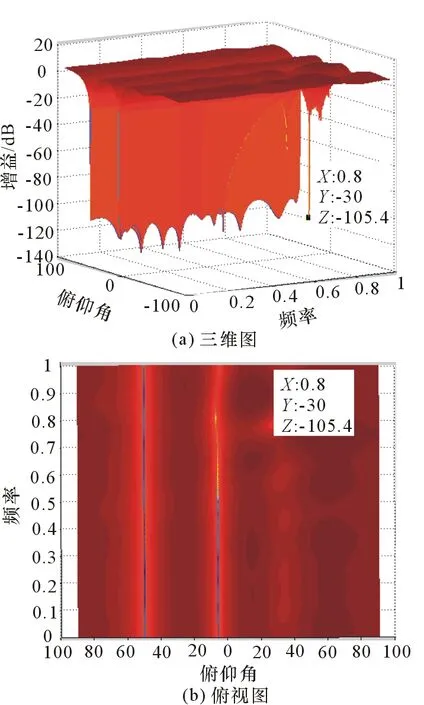
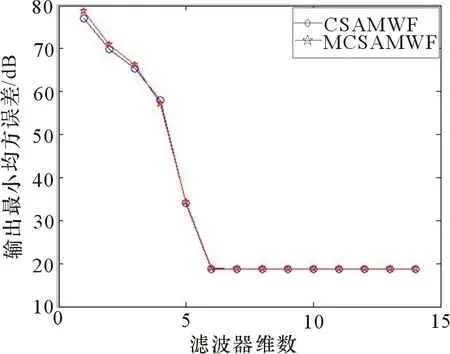
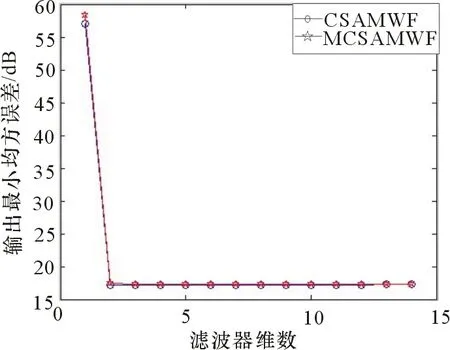
4 仿真试验

5 结束语
