面向AltaRica模型的嵌入式系统安全性验证方法*

仵志鹏，胡 军,2+，陈 松，石娇洁

1.南京航空航天大学 计算机科学与技术学院，南京 210016

2.南京大学 计算机软件新技术国家重点实验室，南京 210093

面向AltaRica模型的嵌入式系统安全性验证方法*

仵志鹏1，胡 军1,2+，陈 松1，石娇洁1

1.南京航空航天大学 计算机科学与技术学院，南京 210016

2.南京大学 计算机软件新技术国家重点实验室，南京 210093

WU Zhipeng,HU Jun,CHEN Song,et al.Safety verification methodology of embedded system based on Alta-Rica model.Journal of Frontiers of Computer Science and Technology,2017,11(1)：24-36.

嵌入式系统；安全性验证；AltaRica模型；Promela模型

1 引言

随着嵌入式系统在航空、航天、能源动力、铁路交通等领域的使用愈加广泛，系统失效可能造成人员伤亡，财产损失，甚至环境危害等可怕后果。因此保证嵌入式系统的安全性和可靠性已然成为软件工程领域研究的热点问题之一[1]。为提高嵌入式系统的安全性和可靠性，针对系统模型的安全性分析与验证已成为系统开发周期中的重要环节。

传统的风险建模分析方法，如故障树分析（fault tree analysis，FTA）[2]、失效模式影响分析（failure mode and effects analysis，FMEA）[3]、Markov Process[4]等在系统安全性分析中广泛使用，但这些建模设计与系统规约形式之间还存在较大不同。AltaRica[5]建模语言可以较好地沟通系统规约形式与建模设计间的形式问题。随着嵌入式系统的复杂度越来越高，嵌入式系统也变得多组件化。组件间交互以及依赖关系的设计成为嵌入式系统安全性分析的关注点，Alta-Rica模型的Dataflow[6]元素能够很好地支持组件间的交互和组件间的依赖关系，同时组件间的依赖关系使用线性时序逻辑（line temporal logic，LTL）[7]进行规约。AltaRica模型结合LTL进行安全性验证无法直接完成，但可以借助模型检验工具SPIN[8]来完成安全性验证。SPIN是被广泛使用的形式化验证模型检测工具，通过系统需求的LTL规约对系统模型穷尽分析完成嵌入式系统的安全性验证。但SPIN并不能直接对AltaRica模型进行验证，此时完成安全性验证必须将AltaRica模型转换成SPIN识别的输入模型——Promela模型。

本文组织结构如下：第2章主要介绍AltaRica语法和Promela语法的形式化描述，并给出面向AltaRica模型的安全性验证框架；第3章给出AltaRica模型到Promela模型[9]的转换规则，并设计原型工具A2STool；第4章使用原型工具A2STool，以机轮刹车系统的机轮刹车控制单元子系统为例进行安全性验证和分析；第5章介绍相关工作；第6章是总结与下一步工作。

2 AltaRica与Promela

为了准确地给出AltaRica模型到Promela模型的转换规则，给出AltaRica语言语法的形式化描述和Promela语言的形式化描述，同时给出面向AltaRica模型的嵌入式系统安全性验证的框架。

2.1 AltaRica的语义

结点node是AltaRica模型的基本组成部分，其他的语法元素都定义在node结点内。node结点根据是否含有子结点分为Equipment类型的结点和Component类型的结点。通用的node结点用九元组N表示，其中：

（1）E是结点中事件的集合；

（2）S是状态变量的集合；

（3）F=FI⋃FO是流变量的集合，FI、FO分别为输入流变量和输出流变量，且FI⋂FO=∅；

（4）I(S)是初始状态;

（5）T(S,FI,ΓE,S′)是转换公式，其中ΓE表示当前事件E发生，其中dom(ΓE)=E；

（6）P:FO→Expr(S)是状态变量表达式与输出变量的映射；

（7）对于∀i=1,2,…,n，九元组N中的，当m≥0时，N中包含零个或多个AltaRica结点；

（8）A(F,N1.F1,N2.F2,…,Nn.Fn)表示流变量不变式的断言区（Ni.Fi是子结点Ni所有流变量的集合）；

（9）V表示两个及以上事件之间的同步关系。

针对九元组N：当S=∅,I=True,T=True且对于任意的f∈FO有P(f)=True，N为Equipment类型；当n=0,A=True且V=∅，N为Component类型。

2.2 Promela的语义

Promela是针对并发系统的建模语言，Promela模型作为成熟的模型检验工具SPIN的输入模型，与SPIN共同完成并发系统的仿真和形式化验证。Promela语言的许多标记从C程序语言中衍化出来，包括布尔语法、算子操作、赋值、等价、变量、参数定义、初始化变量、注释以及指示程序块开始和结束的花括号。Promela模型主要由proctype进程实体组成，一个Promela模型至少包含一个proctype定义，同时也必须要有一个proctype实例。proctype结构体内包含数据定义、其他声明等。

Promela模型中通用的proctype用六元组P表示，其中：

（1）S表示状态集合；

（2）S0∈S表示起始状态；

（3）L是标记的集合，此标记可以是事件或者是要求满足的某种条件；

（4）T⊆(S×L×S)是转移的集合；

（6）F⊆S是终止状态的集合。

2.3 面向AltaRica模型的系统安全性验证框架

面向AltaRica模型的系统安全性验证框架主要包含两方面工作：一方面，通过系统需求对系统组件进行划分，并将其与AltaRica模型元素进行映射，得到系统对应的AltaRica模型以及安全性需求的LTL规约；另一方面，将系统的AltaRica模型利用转换规则转换到Promela模型，结合模型检测工具SPIN进行安全性验证和分析。具体的安全性验证框架如图1所示。

Fig.1 Framework of safety verification forAltaRica model图1 面向AltaRica模型的安全性验证框架

3 AltaRica模型到Promela模型的转换

SPIN是基于形式化方法的模型检测工具，能够对系统性质进行严格的穷尽分析。AltaRica模型能很好地支持系统组件间的交互和组件内的信息传递，特别适合当前多组件系统的建模。因此，针对嵌入式系统的安全性验证可以利用AltaRica模型和SPIN的各自优势，但SPIN并不能直接操作AltaRica模型。使用模型检测工具SPIN需要将AltaRica模型转换为SPIN接受的处理对象——Promela模型，从而完成系统的安全性验证和分析。本节将具体介绍Alta-Rica模型到Promela模型的转换规则和转换规则的证明，以及转换验证工具A2STool的设计。

3.1 转换规则

为便于转换规则的精确定义，首先给出以下定义：A表示AltaRica模型，P表示Promela模型。

（1）结点node的转换

AltaRica模型的node元素和sub元素一方面表示系统组件间的层次关系，另一方面两者都是node结点声明。系统组件在AltaRica模型中映射为结点，系统组件在Promela模型中映射为proctype进程实体，因此AltaRica模型结点转换为proctype元素。精确定义为：N表示AltaRica模型的node结点，sub表示子结点；P表示Promela模型的proctype。因此Alta-Rica模型结点到Promela模型之间的转换规则表示为：AN↔PP&Asub↔PP。转换示例如图2所示。

（2）流变量flow的转换

AltaRica模型的flow元素完成系统组件间和组件内的信息传递，组件内信息传递由flow变量和状态变量完成，组件间信息传递由关联组件的flow变量通过assert元素来完成。

Fig.2 Transform example of node图2 结点的转换示例

①组件内信息传递flow变量的值与状态变量的变化有关，然后通过assert完成绑定，状态变量使用init声明初始化。精确定义为：f和i为AltaRica模型结点flow声明和init声明，State和S0分别为Promela模型中的状态变量和状态初始化。组件内flow声明的转换规则表示为：。转换示例如图3所示。

Fig.3 Transform example of flow and init variable图3 flow变量和init的转换示例

②组件间flow变量表示组件间信息的传递，一般在相关组件的上层组件定义组件间的flow变量，而且flow变量的绑定通过assert声明完成。精确定义：f为AltaRica模型中组件间的flow变量，State表示Promela模型中的状态变量。flow声明的转换规则表示为：Af↔PState。转换示例如图4所示。

Fig.4 Transform example of flow variable图4 flow变量的转换示例

（3）转换trans的转换

AltaRica模型的trans声明和Promela模型状态转移都是系统状态满足一定的条件或在事件的影响下完成。精确定义：T表示AltaRica模型中trans声明，Trans表示Promela模型转换表达式中的状态迁移。因此trans声明的转换规则为：AT↔PTrans。转换示例如图5所示。

Fig.5 Transform example of trans variable图5 trans变量的转换规则

（4）事件event的转换

AltaRica模型的event元素不仅影响组件内状态的迁移，还影响到组件内flow变量以及相关联组件。Promela模型可以使用枚举类型mtype枚举事件，然后定义mtype类型的事件变量Estate表示各个事件。精确定义：E代表AltaRica模型中的event变量，L代表Promela模型的标记。event元素对应的转换规则表示为：AE↔PL。转换示例如图6所示。

Fig.6 Transform example of event variable图6 event变量的转换示例

（5）同步sync的转换

AltaRica模型的同步主要分为3类：强同步、弱同步、CCF同步。

强同步：AltaRica模型中强同步表示形式为sync。强同步具体语义：如果事件e1和e2的同步类型为强同步，则它们在组件c1和c2中对应的状态迁移必须同时发生。Promela模型使用通道chan实现同步。精确定义：sync_strong表示AltaRica模型的强同步，chan表示Promela模型的同步声明。因此强同步的转换规则表示为：Async_strong↔Pchan。转换示例如图7所示。

Fig.7 Transform example of Strong Synchronization图7 Strong Synchronization的转换示例

弱同步：AltaRica模型的弱同步是一种形如广播的同步类型，形式为。弱同步的具体语义：若事件e1和e2同时发生，那么事件对应的转换发生，否则事件e1(e2)发生且事件e2(e1)的守卫条件为true，e1和e2对应的转换都会发生；事件e2(e1)的守卫条件为false，组件e2(e1)对应的转换不发生。精确定义：sync_weak表示AltaRica模型的弱同步，chan表示Promela模型的同步声明。转换规则表示为：Async_weak↔Pchan。弱同步对应的转换示例如图8所示。

Fig.8 Transform example of Weak Synchronization图8 Weak Synchronization的转换示例

CCF同步：CCF同步与弱同步很相似，在AltaRica模型中表示为。两者的区别在于CCF同步的动机是为了描述由于内部错误或共同原因导致组件失效的情形。CCF同步用弱同步来表示，而内部错误和产生失效的共同原因e1、e2认为一个事件影响两个组件的失效。

（6）常量和域的转换

AltaRica模型除了结点node结构外，通常用const和domain关键字定义常量，Promela模型同样在proctype外定义一些常量。针对domain，根据其表示的类型来具体转换，如果是字符型，将其domain声明映射为枚举类型，否则定义为数值变量，同时对变量的值进行区间判断。精确定义：c和d分别表示Alta-Rica模型的常量和域，int和m分别表示Promela模型的常量定义和枚举类型mtypes。常量和域的转换规则表示为：Ac↔Pint,Ad↔Pm。转换示例如图9所示。

Fig.9 Transform example of const and domain图9 const和domain的转换示例

以上给出了AltaRica模型到Promela模型的转换规则和转换示例，转换规则总结如表1所示。

Table 1 Transform rules表1 转换规则

上述转换规则的操作对象是两个模型的状态、流变量、转换、同步、事件等变量，因此并未增加变量，且模型转换过程中的状态空间也是线性增长，状态空间与模型的结点和结点内的变量数决定。假设结点数为n，变量数目为m，那么所占用的状态空间为n×m，且定义的转换规则最终添加到AltaRica模型形成抽象语法树。

3.2 转换规则的正确性证明

由于AltaRica模型和Promela模型的实质是转换系统，模型的语义也都是基于转换系统的精确定义，需要对AltaRica模型和Promela模型进行语义分析。首先给出接口转换系统的语义描述。

定义1（接口转换系统）接口转换系统[10]是一个六元组，其中：

（1）E是事件的集合，ε∈E；

（2）O是观察者的集合；

（3）C是系统状态的集合；

（4）I⊆C是初始状态的集合；

（5）π:C→O每个配置（状态）c∈C到观察者的映射π(c)∈O；

（6）T是状态转移的集合，T∈C×E×C，如，其中c∈C。

接口转换系统是基于包含观察者O和映射函数π在内的标记转换系统，也就是π定义了系统每一个称为配置的状态与O中观察者的映射关系。观察者表示的状态集合可以被另一个接口转换系统所看到，同时观察者通常用来将组件内部状态显示给组件的上层组件，而AltaRica模型的层次结构是其特点之一。标记ε用来定义空事件，含有ε标记的转换表示ITS中的配置（状态）未发生改变。转换暗含ITS的配置未发生改变，用来对异步建模，从而完成ITS间的同步机制。

2.1节和2.2节介绍了AltaRica模型和Promela模型的语义，接下来给出基于接口转换系统两模型的语义描述。

结点分为Equipment类型结点和Component类型结点，因此基于ITS定义结点的语义时也分为Equipment结点的ITS和Component结点的ITS。其中Component类型结点的ITSN定义为：

Equipment类型的结点，ITSN的配置集合C′和初始化状态都是由子结点的配置和观察者的结果组成，对于配置映射π′仅仅和观察者配置相关。然而，转换关系T″的定义很复杂，主要通过如下的步骤进行定义：首先，定义包含同步向量V的所有转换的集合TC，其中局部事件的集合定义为VLOCAL，，同时定义W=Inst(v)×{v}，表示W为同步向量v与同步向量v对应实体笛卡尔积形成的对的集合。此时TC⊆C′×W′×C′包含所有的元素，同时对于所有,对于所有的。

然后，定义集合TB，其主要针对TC进行同步组件转换的最大数进行约束，由此得到的TB转换仅仅在和同步事件相关的组件内转换活动。

最后，定义TA⊆C′×E′×C′约束ITSN的事件E′。满足下面情况之一都有，同时T″=TA。

（1）当e∈E′且时，此时存在w=；

（2）存在c∈C′，满足。

ITS很好地描述了AltaRcia模型的形式化语义，为了更好更精确地进行模型转换，对于Promela模型使用ITS来描述Promela模型的语义。Promela模型进程实体定义为，则基于接口转换系统的语义描述定义为ITSP，，具体的元素对应如下：

ITSP的事件和Promela模型的标记都表示发生状态迁移所需满足的条件或事件；ITSP的配置和ITSP的观察者定义都为状态变量的子集；ITSP中的初始值为Promela模型状态的初始值；ITSP的配置到观察者的映射表示系统状态的子集与观察者内配置的映射。ITSP的转换T′不仅对应Promela模型的转换Trans。

得到基于接口转换系统的AltaRica模型和Promela模型的语义，接下来对3.1节提出的转换规则进行证明。

AltaRica模型的结点N到Promela模型的进程P的转换是正确的，因为基于接口转换系统的ITSN和ITSP是同形异构的。

定理1如果N代表AltaRica模型的结点，P为转换的目的模型Promela的进程实体，那么N基于接口转换系统的定义和P基于接口转换系统的定义等价。

关于AltaRica模型到Promela模型转换的正确性证明：首先ITSN和ITSP的每一个配置都是双射，即满足接口转换系统初始化和不变量配置的状态集相同；然后，ITSN和ITSP的转换也是双射。通过以上存在配置和转换两个双射函数就可以保证实现等价的转换。完整的证明如下。

假设ITSN中每个配置c∈C和每个元组之间存在双向映射关系，同样Promela模型进程实体中每个状态q∈CP和变量VP赋值函数μq之间也存在双向映射关系。

此时，存在一个双射函数ξ：CN→CP，对于给定的由元组定义的状态c∈CN，得到ξ(c)=q，此时q=μq(VP)且μq由确定。定义ξ-1：Q→CN是QP到CN的反映射函数。

现在需要证明ITSN和ITSP的转换关系等价，也就是说的充分必要条件是。

此外，存在3个不相交的集合分别是IdxWeak、IdxSync和Idxε，它们满足如下性质：

（1）IdxWeak⋃IdxSync⋃Idxε={1,2,…,n}，IdxWeak⋂IdxSync=∅，IdxWeak⋂Idxε=∅且IdxSync⋂Idxε=∅；

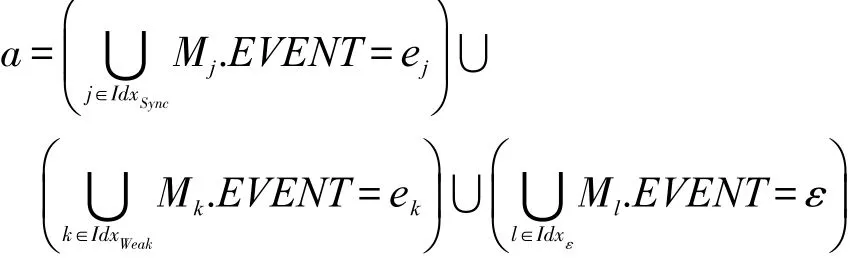
（1）ei=ε且ei′=ε。基于AltaRica的语义，不存在影响状态q迁移的同步向量v2∈V，其中v2=。而且Promela对于空事件i.EVENT=ε的情况时，i不参加同步。

必要性：对于任意的状态q,q′∈CP和任意的事件e∈EP，若q,e,q′∈TransP，则。假定s=ξ-1(q)，s′=ξ-1(q′)，如果，由ITSP的定义得到。完成必要性的证明要求证明存在转换。e有3种可能的形式：

（3）e=v.ec，其中v∈VN，ec∈Inst(v)，基于AltaRica结点的接口转换系统定义得到。此时，若v表示强同步则有；若v表示弱同步，由于，只有q不满足弱同步的守卫条件时才能确保ei=s，因此e是v含有同步实体最多的同步向量，此时。因此TN中存在对应的转换。

3.3 转换工具的设计

根据上述基于AltaRica模型的嵌入式软件安全性分析方法，设计了一款原型分析工具A2STool，其具体设计框架如图10所示。

Fig.10 Design framework ofA2STool图10 A2STool的设计框架

A2STool工具从系统设计出发，主要设计框架分为应用层、业务层和持久层，下面对各层进行说明。

应用层提供了AltaRica模型编辑器、模型转换工具和模型验证功能。

业务层除了接收应用层传过来的操作指令进行业务处理，同时还需要应用层提供AltaRica模型文件和待验证属性。AltaRica模型文件作为整个工具的输入，首先对其使用语法分析工具ANTLR[11]进行语法分析得到语法分析树；然后语法分析树和转换规则结合起来得到目标模型Promela模型文件；最后Promela模型作为验证工具SPIN的输入完成应用层验证功能。

持久层对用户使用过程产生的数据进行管理，例如存取AltaRica模型和转换形成的Promela模型。原型工具的处理流程如图11所示。

Fig.11 Processing flow ofA2STool图11 A2STool的处理流程

上述的处理流程主要分为3个步骤：

（1）A2STool工具的输入过程。主要包括系统设计的AltaRica模型和系统安全性需求的LTL规约。其中AltaRica模型作为直接输入，而安全性需求的LTL规约则用于安全性验证阶段。

（2）A2STool工具的模型转换过程。主要包括语法分析工具ANTLR对AltaRica模型进行语法检查，生成抽象语法树，结合转换规则生成Promela模型。这个转换过程首先需要AltaRica模型的文法文件，图12给出了AltaRica语言的部分文法。转换过程得到的Promela模型作为模型检验工具SPIN的输入。

Fig.12 Part syntax file ofAltaRica language图12 AltaRica语言的文法文件

（3）A2STool工具的验证过程。主要包括模型检验工具SPIN对Promela模型结合安全新需求的LTL规约进行穷尽分析，并完成安全性验证工作。

A2STool原型工具的显示界面如图13所示。

Fig.13 Important page ofA2STool图13 A2STool的主要页面

4 实例分析

本文利用设计的工具对航电系统的机轮刹车系统[12]的控制单元进行安全性验证。首先根据该系统的描述建立起对应的AltaRica模型；然后检查建立的模型语法；接着将AltaRica模型转换到Promela模型；最后通过模型检测工具SPIN对包含安全性需求LTL规约的Promela模型进行安全性验证，并分析验证结果。

4.1 系统描述

机轮刹车系统（wheel brake system，WBS）包含一个数据控制单元，即刹车系统控制单元（brake system control unit，BSCU）以及两个液压线路，即正常线路（由绿色液压泵提供液压值，也可称为绿液压系统）和备用线路（由蓝色液压泵或者蓄压泵提供液压值，也可称为蓝液压系统）。系统从外部环境中读入自动刹车、减速率、飞机速度和打滑的数值信息作为输入。这些数据输入到BSCU中，经过计算产生刹车命令。机轮刹车系统的控制结构如图14所示。

Fig.14 Control unit of wheel brake system图14 机轮刹车系统控制单元

刹车系统控制单元是整个机轮刹车系统中唯一的数据组件。其输入大都来自于更高级别的WBS，位于正常线路和备用线路不同位置上的一些反馈值同时作为本身的输入，而且同时拥有两个独立的电源供应。BSCU由两个子系统构成，两个子系统各自有一个电源进行供应，每个子系统包含有一套命令单元和监控单元。命令单元产生正常命令和备用命令，分别作用于正常线路和备用线路。监控单元主要用于监控对应的命令单元产生的命令是否有效，若两个命令单元均有效，则BSCU有效，并默认使用第一个命令单元的命令；若两个命令单元中只有一个命令是有效的，则BSCU有效，且使用该命令单元产生的命令；若两个命令单元产生的命令均无效，则BSCU无效，两个命令单元产生的命令均不可用。

将WBS的各个组件作为AltaRica模型中的结点，使用UML对BSCU进行描述，如图15所示，该BSCU子系统对应的部分AltaRica模型代码如图16所示。

Fig.15 UML class diagram of BSCU图15 BSCU的UML类图表示

Fig.16 Part code of BSCUAltaRica model图16 BSCU的部分AltaRica模型

4.2 模型转换和验证分析

将4.1节得到的刹车系统控制单元的AltaRica模型导入A2STool工具，依次完成语法检查和模型转换操作，转换后的Promela模型如图17所示。

要保证整个WBS的安全性，首先必须保证BSCU正常工作，由系统需求出发得到如下安全性需求：

Fig.17 Part code of transformed Promela model byA2STool图17 A2STool转换后的部分Promela模型

（1）电源正常（PowerOn=true）工作的情况下，不允许出现BSCU失效（IsBSCU=false）的情况。该安全性需求的LTL规约表示：ltl ss{[]((PowerOn==true) -＞＜＞(IsBSCU==true))}。在A2PSTool工具集成的模型检测工具SPIN的验证结果如图18所示。

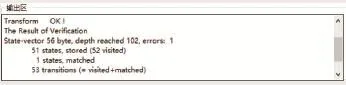
Fig.18 Verification result ofA2STool图18 A2STool下的验证结果

（2）电源正常（PowerOn=true），同时命令单元1产生正常命令（NorCommand=true）的情况下，不允许出现BSCU失效（IsBSCU=false）的情况。该安全性需求的LTL规约表示：ltl ss{[](((PowerOn==true) (NorCommand==true))-＞＜＞(IsBSCU==true))}。在A2STool工具集成的模型检测工具SPIN的验证结果如图19所示。

（1）（2）两个安全性需求验证的结果表明：当前的BSCU设计未考虑如上的两种安全性需求，需重新对BSCU子系统进行设计。本文提出了一套理论方法，对系统安全性设计进行验证，且同类工作较少，只有文献[13]的工作是对AltaRica转换到NuSMV进行验证，采用标记模型检测的方式。而本文采用穷举验证。该实验证明了本文设计的转换规则的正确性，提出了一种解决系统安全性验证的新思路。

Fig.19 Verification result ofA2STool图19 A2STool下的验证结果

5 相关工作

工业界和学术界为了提高安全关键领域嵌入式系统的安全性，系统安全性分析成为系统开发周期中的重要环节。AltaRica作为一种形式化的建模语言，已有很多学者与工业界研究人员在用其进行系统建模以及基于AltaRica进行安全性分析。文献[14]介绍了AirBus和ONERA使用形式化建模语言Alta-Rica及其相应工具对电气和液压系统进行安全性分析的工作。文献[15]介绍了两种经典的模型检验工具SPIN和NuSMV，制定了SPIN到NuSMV模型的转换规则，实现了SPIN到NuSMV输入模型的自动转换。文献[13]介绍了AltaRica模型到HyDI语言的转换，进而使用模型检测工具NuSMV进行安全性评估分析，并对AltaRica模型到HyDI语言的转换进行了证明。文献[16]介绍了在规模和复杂度提高的情况下AltaRica建模方法，解决了建立完整、精确和一致安全模型的困难，对液压系统使用AltaRica进行建模，并进行了安全性分析。文献[17]依据直升机涡轮引擎提出了从初步系统安全性评估分析中推导出软件功能需求的方法。该方法使用AltaRica模型和相应工具从系统失效传播模型中抽取功能失效路径；然后分析此路径得到功能软件需求的最小组合。文献[6]通过风险分析和功能分析来构建AltaRica数据流模型，同时找到SysML与AltaRica数据流模型对应的元素映射。文献[18]使用形式化建模语言Alta-Rica和相应的工具交互仿真系统内部失效的传播，然后通过模型检验验证定性需求以及建立故障树分析产生描述失效事件的序列。文献[19]使用AltaRica语言对空客A320飞机液压系统进行建模，同时展示怎样单独使用故障树生成和模型检测，进而结合二者评估安全需求。与已有工作相比，本文主要从AltaRica模型出发，采用语法分析工具ANTLR对其进行解析得到抽象语法树，最后结合抽象语法树和定义转换规则完成模型转换得到Promela模型。采用模型检验工具SPIN对Promela模型和相应的安全需求的LTL规约进行安全性验证。

6 总结及进一步工作

本文提出了一种采用模型转换和模型验证对嵌入式系统进行安全性验证的方法。同时设计了一款集AltaRica模型编辑功能、模型转换功能、模型验证功能的工具A2STool。首先，将嵌入式系统利用AltaRica建模语言进行建模得到AltaRica模型；其次，使用语法分析工具ANTLR对模型进行解析得到语法树，将其与转换规则结合进行模型转换得到Promela模型；最后，基于Promela模型使用模型检验工具SPIN对安全性需求LTL规约进行验证。通过模型验证找出系统设计的安全性问题，及时进行系统设计调整，提高系统的安全性。

未来的进一步工作主要包括以下两方面：（1）本文给出的转换规则并未包含AltaRica语言的所有元素，将对其他元素的转换规则继续进行研究；（2）将对AltaRica在时间上的扩展作为下一步的研究重点之一。

[1]Huang Zhiqiu,Xu Bingfeng,Kan Shuanglong,et al.Survey on embedded software safety analysis standards,methods and tools for airborne system[J].Journal of Software,2014, 25(2):200-218.

[2]Xu Bingfeng,Huang Zhiqiu,Hu Jun,et al.Time property analysis method for state/event fault tree[J].Journal of Software,2015,26(2):427-446.

[3]Medikonda B S,Ramaiah P S,Gokhale A A.FMEA and fault tree based software safety analysis of a railroad crossing critical system[J].Global Journal of Computer Science andTechnology,2011,11(8):57-58.

[4]Zhou Guochang,Guo Baolong,Gao Xiang,et al.Research on the system reliability modeling based on Markov process and reliability block diagram[C]//Proceedings of the 1st Euro-China Conference on Intelligent Data Analysis and Applications,Shenzhen,China,Jun 13-15,2014.[S.L]:Springer International Publishing,2014:545-553.

[5]Griffault A,Lajeunesse S,Point G,et al.The AltaRica language[C]//Proceedings of the 1998 International Conference on Safety and Reliability,1998:20-24.

[6]David P,Idasiak V,Kratz F.Automating the synthesis ofAlta-Rica data-flow models from SysML[M]//Reliability,Risk and Safety:Theory and Applications.London:Taylor& Francis Group,2009:105-112.

[7]Pnueli A.The temporal logic of programs[C]//Proceedings of the 18th Annual Symposium on Foundations of Computer Science,1977:46-57.

[8]Clarke E M,Grumberg O,Peled D.Model checking[M]. Cambridge,USA:MIT press,1999.

[9]Inverardi P,Muccini H,Pelliccione P.Automated check of architectural models consistency using SPIN[C]//Proceedings of the 16th Annual International Conference on Automated Software Engineering,San Diego,USA,Nov 26-29,2001. Piscataway,USA:IEEE,2001:346-349.

[10]Parr T J,Quong R W.ANTLR:a predicated-LL(k)parser generator[J].Software:Practice and Experience,1995,25 (7):789-810.

[11]Arnold A,Point G,Griffault A,et al.The AltaRica formalism for describing concurrent systems[J].Fundamenta Informaticae,1999,40(2/3):109-124.

[12]Joshi A,Heimdahl M P E,Miller S P,et al.Model-based safety analysis[R].Contractor Report Cecilia Haskins,Nasa Langley Research Center,2006.

[13]Bozzano M,Cimatti A,Lisagor O,et al.Safety assessment of AltaRica models via symbolic model checking[J].Science of Computer Programming,2015,98:464-483.

[14]Bieber P,Bougnol C,Castel C,et al.Safety assessment with Altarica[C]//Building the Information Society:IFIP 18th World Computer Congress Topical Sessions,Toulouse, France,Aug 22-27,2004.[S.l.]:Springer US,2004:505-510.

[15]Jiang Yong,Qiu Zongyan.S2N:model transformation from SPIN to NuSMV[C]//LNCS 7385:Proceedings of the 19th International Workshop on Model Checking of Software, Oxford,UK,Jul 23-24,2012.Berlin,Heidelberg:Springer, 2012:255-260.

[16]Li Shaojun,Duo Su.A practicable MBSA modeling process using AltaRica[C]//LNCS 8822:Proceedings of the 4th International Symposium on Model-Based Safety and Assessment,Munich,Germany,Oct 27-29,2014.[S.l.]:Springer International Publishing,2014:1-13.

[17]Humbert S,Seguin C,Castel C,et al.Deriving safety software requirements from an AltaRica system model[C]// LNCS 5219:Proceedings of the 27th International Conference on Computer Safety,Reliability,and Security,Newcastle upon Tyne,UK,Sep 22-25,2008.Berlin,Heidelberg: Springer,2008:320-331.

[18]Zhu Yuanzhen,Zhang Jianguo,Gong Qi,et al.Reliability and safety assessment with AltaRica for complex aircraft systems[C]//Proceedings of the 2011 9th International Conference on Reliability,Maintainability and Safety,Guiyang, China,Jun 12-15,2011.Piscataway,USA:IEEE,2011:588-593.

[19]Bieber P,Castel C,Seguin C.Combination of fault tree analysis and model checking for safety assessment of complex system[C]//LNCS 2485:Proceedings of the 4th European Dependable Computing Conference,Toulouse,France, Oct 23-25,2002.Berlin,Heidelberg:Springer,2002:19-31.

附中文参考文献：

[1]黄志球,徐丙凤,阚双龙,等.嵌入式机载软件安全性分析标准、方法及工具研究综述[J].软件学报,2014,25(2): 200-218.

[2]徐丙凤,黄志球,胡军,等.一种状态事件故障树的时间特性分析方法[J].软件学报,2015,26(2):427-446.

WU Zhipeng was born in 1989.He is an M.S.candidate at Nanjing University of Aeronautics and Astronautics.His research interests include software safety analysis and model checking,etc.

仵志鹏（1989—），男，河南周口人，南京航空航天大学硕士研究生，主要研究领域为软件安全性分析，模型检测等。

HU Jun was born in 1973.He received the Ph.D.degree in computer software and theory from Nanjing University in 2006.Now he is an associate professor at Nanjing University of Aeronautics and Astronautics,and the member of CCF.His research interests include model-based safety analysis,software verification and embedded system design,etc.

胡军（1973—），男，湖北黄冈人，2006年于南京大学计算机软件与理论专业获得博士学位，现为南京航空航天大学计算机科学与技术学院副教授，CCF会员，主要研究领域为模型驱动的系统安全性分析，软件验证，嵌入式系统设计等。主持过航空基金、教育部博士点基金、国防预研基金、教育部留学人员启动基金、南京航空航天大学科技创新基金等项目，并参与多项国家自然科学基金、国防预研以及863计划等项目。

CHEN Song was born in 1991.He is an M.S.candidate at Nanjing University of Aeronautics and Astronautics.His research interests include software safety analysis and model checking,etc.

陈松（1991—），男，山东泰安人，南京航空航天大学硕士研究生，主要研究领域为软件安全性分析，模型检测等。

SHI Jiaojie was born in 1990.She is an M.S.candidate at Nanjing University of Aeronautics and Astronautics.Her research interests include software safety analysis and model checking,etc.

石娇洁（1990—），女，河南郑州人，南京航空航天大学硕士研究生，主要研究领域为软件安全性分析，模型检测等。

Safety Verification Methodology of Embedded System Based onAltaRica Model*

WU Zhipeng1,HU Jun1,2+,CHEN Song1,SHI Jiaojie1
1.College of Computer Science and Technology,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China
2.State Key Laboratory for Novel Software Technology,Nanjing University,Nanjing 210093,China
+Corresponding author:E-mail:wuzhipeng2013@nuaa.edu.cn

As the embedded system is widely used in the safety-critical fields such as aeronautics,astronautics and transportation,AltaRica is a kind of formal modeling languages for safety-critical systems.Modeling critical systems based on AltaRica model and the safety analysis upon this have become the industrial standard in Europe.This paper proposes a kind of embedded system safety verification method based on AltaRica model,which includes, firstly model the embedded system using AltaRica,then exhibit the transformation rules from AltaRica model to Promela model,at the same time do formal proofs on transformation rules,so as to acquire the Promela model of embedded system,and finally use SPIN,a model check tool,to analyze and verify it.This paper takes the control unit of wheel brake system as an example to verify this transformation rules and method.

embedded system;safety verification;AltaRica model;Promela model

A

：TP311.5

10.3778/j.issn.1673-9418.1511003

*The National Basic Research Program of China under Grant No.2014CB744903(国家重点基础研究发展计划(973计划));the Scientific Research Foundation for the Returned Overseas Chinese Scholars,State Education Ministry of China under Grant No.2012(教育部回国留学人员科研启动基金);the Science Foundation for Youth Science and Technology Innovation of Nanjing University of Aeronautics andAstronautics under Grant No.NS2014098(南京航空航天大学青年科技创新基金).

Received 2015-11,Accepted 2016-02.

CNKI网络优先出版:2016-02-19,http://www.cnki.net/kcms/detail/11.5602.TP.20160219.1651.002.html

摘 要：嵌入式系统在航空、航天、交通等安全关键领域的使用愈加广泛，AltaRica是一种描述安全关键系统的建模语言，同时基于AltaRica模型的安全性分析已成为欧洲的工业标准。提出了一种面向AltaRica模型的嵌入式系统安全性验证方法，包括：使用AltaRica语言对嵌入式系统进行建模；给出AltaRica模型到Promela模型的转换规则；对转换规则进行形式化证明，得到嵌入式系统的Promela模型；使用模型检验工具SPIN进行安全性验证。通过机轮刹车系统中的机轮刹车控制单元进行实例分析，验证了转换规则的正确性和有效性。