稀疏表示的无参考图像质量评价方法*

桑庆兵，程大宇

江南大学 物联网工程学院，江苏 无锡 214122

稀疏表示的无参考图像质量评价方法*

桑庆兵+，程大宇

江南大学 物联网工程学院，江苏 无锡 214122

SANG Qingbing,CHENG Dayu.Blind image quality assessment via sparse representation.Journal of Frontiers of Computer Science and Technology,2017,11(1)：144-154.

现有的无参考图像质量评价算法多采用支持向量回归、神经网络等作为映射，训练过程需要大量样本，且泛化性能差（即在一个数据集上的训练识别效果好，在另一个数据集上可能很差），从而提出了基于稀疏表示的无参考图像质量评价算法。利用梯度幅值与拉普拉斯变换图像的联合统计信息和小波变换子带相关性组成特征字典，并对测试图像特征进行稀疏表示，最后综合稀疏系数与字典图像DMOS值获得预测质量得分。多数据库中大量实验结果表明，新算法在少量训练样本条件下即可获得优良而稳定的结果，且具有更好的泛化性能和稳定性。

无参考图像质量评价；稀疏表示；统计特征；小波交换

1 引言

在人类感知世界和相互交流的过程中，视觉信息扮演着重要的角色。近年来，随着数字图像和互联网技术的发展，越来越多的人开始拍摄、传递数字图像。据统计，仅美国社交网络用户每年拍摄图片数量就达1 000亿张之多[1]。在图像的采集、压缩、传输、显示等过程中，诸多因素可能会导致图像视觉质量受到影响。因此，对于图像质量评价算法的研究具有重要的意义。

图像质量评价包括主观评价与客观评价两大类，前者由人直接对图像质量打分；后者则通过给定的模型和输入的特征指标对图像质量进行预测。主观评价虽具有较高的可靠性，但耗时长，费用高，难操作，在研究中客观评价方法更受学者关注。根据对参考图像的依赖程度，客观评价可分为全参考型、半参考型和无参考型。全参考型方法需要获得参考图像进行质量评价，典型的全参考质量评价方法有峰值信噪比（peak signal to noise ratio，PSNR）、基于结构相似度方法（structural similarity，SSIM）[2]等。半参考型方法则需要参考图像的部分信息，代表性的半参考质量评价方法包括混合图像质量评价方法（hybrid image quality metric，HIQM）[3]、多尺度几何分析法（multiscale geometric analysis，MGA）[4]等。然而多数图像的获取具有随机性，质量评价过程中无法获得参考图像。因此不依赖参考图像的无参考图像质量评价更具有实用价值。

研究表明，自然场景图像统计信息具有一定规律性，而图像引入失真后，统计信息分布会产生变化，这为无参考图像质量评价提供了依据。根据应用范围的不同，无参考图像质量大体可分为专用型和通用型两大类。专用型方法只针对某一类失真图像进行质量评价，如模糊、压缩、噪声等。然而实际操作中失真类型存在着不确定性，专用型方法的应用受到了很大限制。通用型方法主要包括两类：一类是两阶段框架，此类算法首先确定图像失真类型，再选择对应算法进行评价。典型的两阶段框架算法有BIQI（blind image quality index）[5]、DIIVINE[6]等。BIQI根据图像小波域统计特征对失真类型分类，再利用回归模型给出图像质量的预测值；DIIVNE在小波子带中提取88维统计特征，接着通过支持向量回归（support vector regression，SVR）建立模型对图像质量进行预测。另一类是全局框架，此类算法不区分图像失真类型，直接对图像进行评价。代表性的全局框架算法有BLIINDS-II（blind image integrity notator using DCT statistics-II）[7]、GRNN（general regression neural network）[8]、BRISQUE（blind/referenceless image spatial quality evaluator）[9]等。BLIINDS-II对图像进行离散余弦变换（discrete cosine transform，DCT）后提取变换域中的对比度、清晰度等感知特征和统计特征，采用概率模型预测图像质量。GRNN提取相位一致性（phase congruency，PC）、梯度、熵等感知特性，通过广义神经网络构建了感知特征与主观评价得分之间的映射，从而预测图像质量。BRISQUE直接对图像空域统计特征进行研究，利用SVR建立空间统计特征与主观评价得分之间的映射，计算图像预测值。

Xue等人[10]提出一种联合统计图像局部对比度特征的无参考图像质量评价方法。该方法首先分别计算图像的梯度幅值（gradient magnitude，GM）和拉普拉斯变换图像（Laplacian of Gaussian，LOG），对二者进行联合自适应归一化（joint adaptive normalization，JAN）。接着计算归一化后梯度特征和拉普拉斯特征的边缘分布以及去除相关性后二者的独立分布作为特征信息。最后使用支持向量回归对图像质量进行预测。本文在此基础上结合小波变换子带的相关性信息，将训练图像特征按列排列组成字典，并对测试图像特征进行稀疏表示，利用稀疏系数进行图像质量评价。

2 空域特征提取

自然图像作为一种高维信号包含着很多冗余信息，图像统计特征的提取可以看作是去除冗余将信息降维的过程。近年来，针对自然图像的空域特征提取成为无参考图像质量评价领域的发展趋势，如BRISQUE、IL-NIQE[11]等。对梯度幅值和拉普拉斯变换图像进行联合自适应归一化提取特征的方法如下。

计算图像I的梯度幅值GI与拉普拉斯响应LI：

图1展示了LIVE数据库中同一幅参考图像加入失真后，不同DMOS值失真图像的边缘分布PG（左半边）和PL（右半边）。可以看出，随失真程度的增加，直方图变化率增加明显。这说明PG和PL可以用来预测图像质量。

Fig.1 Marginal probabilities of different distorted images generated from same reference image图1 一幅参考图像加入不同失真后的边缘分布

特征之间的相关性过大不但会造成数据冗余，降低运算速度，而且可能对揭示图像质量的信息（分类特征）造成覆盖、污损，改变特征间的相似度，进而使特征与图像质量间的映射发生改变，影响预测模型的精确度。考虑到梯度特征与拉普拉斯特征的相关性，定义：

为了去除二者相关性，对于每个G=gm对应的所有L值的相关性，使用边缘分布P(G=gm)作为权重。定义下式为G=gm时对L的整体相关性。

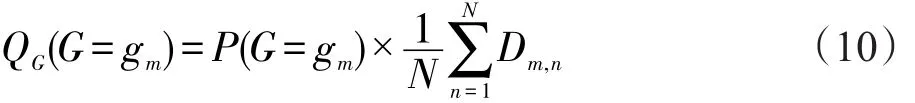
类似的，定义下式为L=ln时对G的整体相关性:

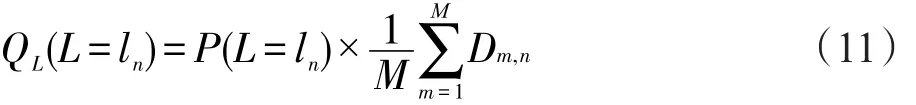
容易证明，QG≥0，QL≥0，且∑mQG(G=gm)=∑nQL(L=ln)=1。因此，在某种程度上可以将其认为是概率分布，称之为独立分布。

QG和QL可以写成：

图2为LIVE数据库中同一幅参考图像加入失真后，不同DMOS值失真图像的独立分布QG（左半边）和QL（右半边）。与图1一样，随图像失真程度的增加，对应直方图变化率增加明显。因此，QG和QL也可以作为预测图像质量的依据。

Fig.2 Independency distributions of different distorted images generated from same reference image图2 一幅参考图像加入不同失真后的独立分布

从式（10）、（11）中可以得到关于G的边缘分布PG共M维，关于L的边缘分布PL共N维。从式（12）、（13）中可以得到PG的独立分布QG共M维，PL的独立分布QL共N维。理论上M、N等级数越高，统计特征越稳定，预测结果越精确。但是等级数的增加会影响运行速度，而且需要大量的训练样本。考虑到实际应用效果，实验中取M=N=10，得到PG、PL、QG、QL各10维，组成40维空域统计特征。

3 频域特征提取

灰度共生矩阵（gray level co-occurrence matrix，GLCM）是通过统计图像上相隔一定距离的两个像素点灰度值之间空间相关关系得到的，它反映了纹理图像中各灰度级在空间上的分布特性[12]。在一幅图像I(N×N)中任取一点(x,y)，其灰度值为g1，及偏离它的另一点(x+a,y+b)，其灰度值为g2，得到一组灰度对(g1,g2)。令该点在整幅图上按指定方向和间距移动，得到各种灰度对组合。设图像的灰度级数为k，可知(g1,g2)组合共有k2种。统计(g1,g2)的联合概率密度分布就得到了图像I的灰度共生矩阵。(a,b)的取值可以根据图像纹理周期分布特性进一步进行选择。本文采用默认值。

相关性（correlation，COR）是用来度量灰度共生矩阵元素在行或列方向上的相似程度。因此，相关性值大小反映了图像中局部灰度相关性。当矩阵元素在行或列值均匀相等时，相关值就大；相反，如果值相差很大，则相关值就小。式（16）是相关性的计算公式：

其中，μx、μy为均值；σx、σy为方差。

Fig.3 Reference image and its subbands图3 参考图像及其子带

小波变换因其多分辨率和多方向等特性可以很好地模拟人类视觉系统认知图像的过程，有助于提高图像特征的准确性。图3为一幅参考图像与其水平方向小波分解高频图像。可以看出，5个尺度的高频图像均较好地表现了参考图像中的轮廓信息，可以作为判断图像质量的依据。考虑到小波分解下采样的特性，更低尺度的高频图像将丢失大量图像细节信息，因此这里计算小波分解5个尺度各子带的相关性。

图4为LIVE数据库中29幅参考图像各子带相关性分布。横轴为子带顺序（1～5为水平方向子带，6～10为对角线方向子带，10～15为垂直方向子带），纵轴为相关性值。图5为一幅参考图像引入不同程度失真后对应的子带相关性分布，y1～y5失真程度依次增加。

观察图4可知，不同参考图像水平方向与对角线方向各子带的相关性变化趋势较为平缓，且差值不大。而垂直方向各子带的相关性并不具有相同的变化趋势或相近的数值。图5中，同一幅图像随失真程度的增加，水平方向和对角线方向各子带的相关性变化趋势骤增。与图4相似，垂直方向各子带的相关性依然不具有任何规律性。因此认为，小波变换水平方向和对角线方向各子带的相关性可作为特征对图像质量进行预测。这里取5个尺度子带的相关性，组成10维频域特征。

Fig.4 Correlation of subbands of 29 reference images on LIVE database图4 LIVE数据库中29幅参考图像各子带相关性

Fig.5 Correlation of subbands of different distorted images from one reference image图5 一幅参考图像引入不同程度失真后各子带相关性

4 基于稀疏表示质量评价模型

近年来，以信号的稀疏性先验求解图像反问题引起了学者们的广泛关注[13]。作为人类视觉系统的重要特征之一，稀疏表示可以很好地模拟人眼对物体的感知认识过程。对于一个信号y，求其在超完备字典D上的稀疏系数可概括成如下优化问题：

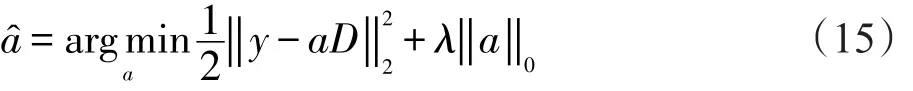
其中，是希望得到的稀疏系数；λ是权衡信号重构后保真度与稀疏性的参数。式（15）的第一项表示在优化后得到稀疏系数a，可以足够精确地表示信号y。而第二项则是求稀疏系数a的l0范数，即a中非零项的个数。通过上述优化过程即可得到一个足够稀疏且可准确表示信号y的向量。然而，该过程中l0范数最小化被证明是一个NP难问题。2004年，Donoho[14]证明了在足够稀疏的情况下，可以用l1范数替代l0范数。上式可以写成：

信号的重构精度与系数的稀疏性成正比[15]，因此字典的合理选取尤为重要。自然图像的复杂性、随机性、高维性等特点使得如傅里叶变换、小波变换等基于解析方法构造的字典无法对其最优表示。本文使用训练集特征直接组成字典，这样字典原子能与待测图像特征结构更好地匹配，获得更稀疏的表示系数，从而保证图像质量预测值的精确性。具体过程如下：首先提取训练样本中各幅图像空域特征Q(QL,QG)和频域特征W。将每幅图像特征按列排列，构成一个字典元素fk，各元素按行排列组成字典D(f1…fk…fT，其中T为训练集图像数，且T大于fk维数）。接着对测试图像以相同方式提取特征fp，并使用字典D对其进行稀疏表示。稀疏表示的过程可以看作对方程组求解，因为方程数小于未知数的个数，所以方程组有无数组解。而式（16）的约束条件既保证了使用方程组解重构信号的保真度，又平衡了方程组解的稀疏性，使其大部分为零。少数非零系数值的大小就是该系数对应字典元素对信号重构做出的贡献度。

最后，利用稀疏系数作为权重对测试图像的质量进行预测，这个过程如图6所示。为了突出稀疏系数对重构信号的贡献度，这里取稀疏系数a^与其绝对值乘积A作为权重用以计算。

测试图像的预测值可由如下公式得出：

其中，dmos为字典各元素对应的DMOS值；为稀疏系数；dmosp为测试图像预测质量分数。

本文图像质量算法评价模型如图7所示。

Fig.6 Process of image feature extract and sparse representation图6 图像的特征提取和稀疏表示过程

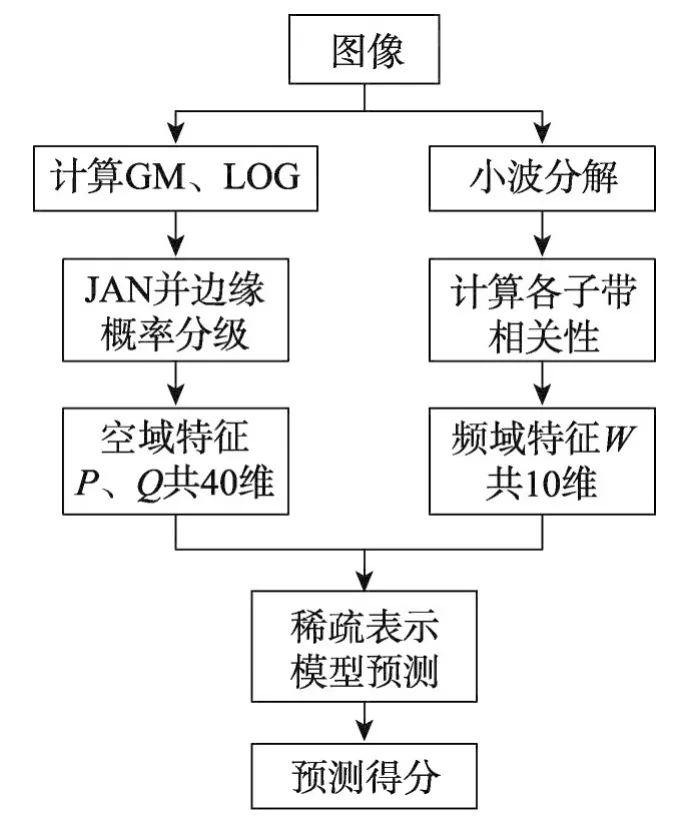
Fig.7 IQAmodel of this paper图7 本文图像质量评价模型

5 实验结果及分析

为验证本文算法性能，在LIVE[16]、TID2008[17]和CSIQ[18]数据库中进行测试。LIVE数据库包括29幅参考图像和779幅失真图像和每幅图像对应的差分平均主观分数（differential mean opinion scores，DMOS）。失真种类包括JPEG2000、JPEG、高斯模糊（Gaussian blur，GBLUR）、高斯白噪声（white Gaussian noise，WN）和快速衰落（fast fading，FF），DMOS值的范围在0～100之间，数值越小代表图像越清晰，反之则越模糊。TID2008数据库由25幅参考图像和17种失真对应的1 700幅图像组成，并包括每幅图像的平均主观分数（mean opinion scores，MOS）。MOS取值范围在0～9之间，数值越大代表图像越清晰，反之则越模糊。CSIQ数据库由30幅参考图像和6种失真对应的866幅失真图像组成，同时给出每幅图像的DMOS值，其范围在0～1之间，数值越小表示图像越清晰，反之则越模糊。

实验中，采用Pearson线性相关系数（Pearson's linear correlation coefficient，PLCC）和Spearman等级相关系数（Spearman's rank ordered correlation coefficient，SROCC）作为衡量算法性能的指标。其中PLCC系数主要用来评价预测值的准确性，SROCC系数主要评价预测值与主观值间的相关性。二者的取值均在0～1之间，数值越大表示预测结果越好。对得到的预测值进行非线性逻辑回归，回归函数如下：

其中，Q是预测值；Qp是回归后的预测值；β1为预测质量集中的最小值；β2为测试图像质量集中的最大值；β3为预测质量集的均值；β4=β5=1。

5.1 在LIVE数据库上的实验

为了确保特征选择的合理性，并进一步验证去相关性过程的实际效果，这里将特征集分为3组进行测试。S1由边缘分布特征P与频域特征W组成，共30维；S2由独立分布特征G与频域特征W组成，共30维；S3由空域特征P、Q与频域特征W组成，共50维。测试首先随机抽取LIVE数据库中80%的图像作为训练集对模型进行训练，另外20%图像作为测试集。进行100次实验后取中值代表实验性能。对比数据选取了经典的全参考（FR）图像质量评价方法PSNR和SSIM，以及较新的无参考（NR）算法BRISQUE等。实验结果如表1、表2所示。

Table 1 Spearman's rank ordered correlation coefficient on LIVE database表1 LIVE数据库中Spearman等级相关系数

Table 2 Pearson's linear correlation coefficient on LIVE database表2 LIVE数据库中Pearson线性相关系数

综合表1、表2可知，在本文提出的3组特征中，去除了相关性的S2在各项实验中几乎均优于未去除相关性的S1，这表明去相关性过程对于优化特征，提高算法性能具有一定效果。相较S1、S2，S3特征维数有所增加，但各项实验结果均超过前两者，因此采用S3作为模型特征进行实验。

图8和图9分别为LIVE数据库中Spearman等级相关系数和Pearson线性相关系数箱线图。本文算法（S3）与全参考算法相比，在JP2K、WN和FF失真上各有高低，相差不大，在JPEG和GBLUR失真上更具优势，且总体结果远高于二者。与无参考算法相比，本文算法的JPEG失真与BRISQUE算法存在一定差距，WN失真虽略低于最高值，但结果也比较高，其他失真类型和总体性能上均表现优秀，在FF失真类型上的优势最大。

Fig.8 Box plot of Spearman's rank ordered correlation coefficient on LIVE database图8 LIVE数据库中Spearman等级相关系数箱线图

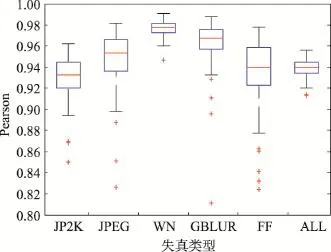
Fig.9 Box plot of Pearson's linear correlation coefficient on LIVE database图9 LIVE数据库中Pearson线性相关系数箱线图

5.2 泛化性能实验

为了检验本文算法的泛化性能，进行了数据库交叉实验。由于TID2008数据库中没有FF失真图像，这里使用LIVE数据库中其他4种失真类型图像作为训练集生成字典，对TID2008数据库中对应的4种失真类型图像进行质量评价。本文算法特征提取是基于自然场景统计信息，因此TID2008数据库中的人工图像（第25幅）及其失真图像暂不考虑。为了简便，这里仅列出对应的Spearman系数作对比，Pearson系数亦有相同的趋势。实验数据如表3所示。

从表3可知，本文算法在数据库交叉实验中，除在WN失真上存在明显差异外，其他各指标均有较好表现。图10表明，在交叉实验中各失真类型主观值与预测值基本成线性关系，模型特征选取较为合理。算法整体预测性能较高，与人眼主观评价具有较高的一致性，且不依赖于训练集的内容，泛化性能较强。

Table 3 Spearman's rank ordered correlation coefficient on TID2008 database表3 TID2008数据库中Spearman等级相关系数

5.3 稳定性实验

为了验证本文算法的稳定性，在LIVE、TID2008和CSIQ数据库上，对每个数据库分别取其中80%、50%、30%图像作为训练集，剩余图像作为测试集进行测试，并与较新的图像质量评价法进行比较。由于篇幅所限，这里仅列出Spearman系数，结果如表4所示（参考文献[19]中的数据）。

Fig.10 Scatter plot of different distortions on TID2008 database图10 TID2008数据库各失真类型散点图

对于正交基构成的完备字典，每一个特征向量的表示几乎需要字典所有原子参与，且存在唯一的字典原子线性组合。这不但降低了字典的表达能力，更增加了表示过程对字典原子数量和种类的依赖性。而在过完备字典中，特征向量的表示存在多组解，可根据不同条件选取最优表示。由于本文特征选取准确合理，DMOS相近的图像具有同一类特征。当训练集比例减少时，虽然各类特征的丰富程度有所降低，但字典的冗余性保证了在缺少最佳原子的情况下仍能较准确地对特征进行表示，从而保证了预测模型在少量训练集情况下的准确性和稳定性。

由表4可知，本文算法仅在LIVE数据库中训练集占80%比重的实验中结果略低于BRISQUE算法，在其他比重及另外两个数据库上的所有结果均明显占优，尤其在训练集比重较低情况下，本文算法数据优势更加明显。此外，不同比例训练集实验结果的标准差统计显示，本文算法各项标准差均最小。综上可知，本文算法预测结果受训练集影响较小，在训练集比例波动情况下仍能获得良好效果，更加具有稳定性。

5.4 时间性能实验

为验证本文算法时间性能，在Intel Core i3-M350 CPU 2.27 GHz，内存2 GB，操作系统32位Windows 7旗舰版PC机上，使用Matlab 2011b，对一幅像素为768×512的LIVE数据库彩色图像进行处理，运行时间如表5所示。

由表5可知，本文算法在时间性能上远优于BLIINDS-II、DIIVIE两种算法，与BRISQUE相比速度稍慢，但也已达到快速评价的效果，0.01 s的差值在实际操作中几乎无差别。

Table 4 Spearman's rank ordered correlation coefficient of experiment with different proportion of training sets表4 采用不同比例训练集测试的Spearman等级相关系数

Table 5 Comparison of time performance表5 时间性能比较

6 结束语

信号稀疏表示理论自20世纪90年代提出以来，便得到了大批学者的关注，并在信号压缩、识别与分类以及图像融合、图像去噪、图像复原等相关领域得到广泛应用。但是其在图像质量评价方面的应用尚属发展阶段。本文结合空域和频域统计特征，使用稀疏表示建立无参考图像质量评价模型。在各标准数据库中的实验结果表明，本文算法与主观评价具有较高的一致性，且泛化性能强，稳定性高，具有较好的综合能力。

自然图像的表示存在着稀疏性[20]。基于此理论，利用聚类生成码本并建立码本与图像质量关系的图像质量评价方法[19，21]获得了良好的结果。在此类算法中，使用稀疏表示对码本进行优化，可以丰富码本信息，从而提高预测精度。在3D图像质量评价中，对深度信息的利用是一个难点。稀疏性作为人类视觉系统的重要特点，将其应用到视差图、深度图的研究中，相信会对提高3D图像质量评价算法性能做出一定贡献。接下来，会针对上述问题进行深入研究。

[1]Taegeun O,Jincheol P,Kalpana S,et al.No-reference sharpness assessment of camera-shaken images by analysis of spectral structure[J].IEEE Transactions on Image Processing, 2014,23(12):5428-5439.

[2]Wang Zhou,Bovik A C,Sheikh H R,et al.Image quality assessment from error visibility to structural similarity[J].IEEE Transaction on Image Processing,2014,13(4):600-612.

[3]Kusuma T,Zepernick H.A reduced-reference perceptual quality metric for in-service image quality assessment[C]// Joint First Workshop on Mobile Future and IEEE Symposium on Trends in Communications,Bratislava,Slovakia, Oct 26-28,2003.Piscataway,USA:IEEE,2003:71-74.

[4]Gao Xinbo,Lu Wen,Tao Dacheng,et al.Image quality assessment based on multiscale geometric analysis[J].IEEE Transactions on Image Processing,2009,18(7):1409-1423.

[5]Moorth A K,Bovik A C.A two-step framework for constructing blind image quality indices[J].IEEE Signal Processing Letters,2010,17(5):513-516.

[6]Moorth A K,Bovik A C.Blind image quality assessment: from natural scene statistics to perceptual quality[J].IEEE Transactions on Image Processing,2011,20(12):3350-3364.

[7]Saad M,Bovik A C,Charrier C.DCT statistics model-based blind image quality assessment[C]//Proceedings of the 18th IEEE International Conference on Image Processing,Brussels,Belgium,Sep 2011.Piscataway,USA:IEEE,2011:3093-3096.

[8]Li Chaofeng,Bovik A C,Wu Xiaojun.Blind image quality assessment using a general regression neutal network[J]. IEEE Transactions on Neural Networks,2011,22(5):793-799.

[9]Mittal A,Moorthy A K,Bovik A C.No-reference image quality assessment in the spatial domain[J].IEEE Transactions on Image Processing,2012,21(12):4695-4708.

[10]Xue Wufeng,Mou Xuanqin,Zhang Lei,et al.Blind image quality assessment using joint statistics if gradient magnitude and Laplacian features[J].IEEE Transactions on Image Processing,2014,23(11):4850-4862.

[11]Zhang Lin,Zhang Lei,Bovik A C.A feature-enriched completely blind image quality evaluator[J].IEEE Transactions on Image Processing,2015,24(8):2579-2591.

[12]Sang Qingbing,Li Chaofeng,Wu Xiaojun.No-reference blurred image quality assessment based on gray level cooccurrence matrix[J].Pattern Recognition and Artificial Intelligence,2013,26(5):492-497.

[13]Lian Qiusheng,Shi Baoshun,Chen Shuzhen.Research advances on dictionary learning models,algorithms and applications[J].Acta Automatica Sinica,2015,41(2):240-260.

[14]Donoho D L.For most large underdetermined systems of equations,the minimal 1-norm near-solution approximates the sparsest near-solution[J].Communications on Pure and Applied Mathematics,2006,59(7):907-934.

[15]Donoho D L.Compressed sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306.

[16]Sheikh H R,Wang Zhou,Cormack L,et al.LIVE image quality assessment database release 2[DB/OL].(2007-06-30) [2013-12-03].http://live.ece.utexas.edu/research/quality/.

[17]Ponomarenlo N,Lukin V,Zelensky A,et al.TID2008—a database for evaluation of full-reference visual quality assessment metrics[J].Advances of Modern Radioelectronics, 2009,10(5):35-40.

[18]Larson E C,Chandler D M.Most apparent distortion:fullreference image quality assessment and the role of strategy [J].Journal of Electronic Imaging,2010,19(1):143-153.

[19]Xue Wufeng,Zhang Lei,Mou Xuanqin.Learning without human scores for blind image quality assessment[C]//Proceedings of the 2013 IEEE Conference on Computer Vision and Pattern Recognition,Portland,USA,Jun 23-28,2013. Piscataway,USA:IEEE,2013:995-1002.

[20]Olshausen B A,Field D J.Emergence of simple-cell receptive field properties by learning a sparse code for natural images[J].Nature,1996,381(6583):607-609.

[21]Ye Peng,Doermann D.No-reference image quality assessment using visual codebooks[J].IEEE Transactions on Image Processing,2012,21(7):3129-3138.

附中文参考文献：

[12]桑庆兵,李朝锋,吴小俊.基于灰度共生矩阵的无参考模糊图像质量评价方法[J].模式识别与人工智能,2013,26 (5):492-497.

[13]练秋生,石保顺,陈书贞.字典学习模型、算法及其应用研究进展[J].自动化学报,2015,41(2):240-260.

SANG Qingbing was born in 1973.He received the Ph.D.degree in image processing from Jiangnan University in 2013.Now he is an associate professor and M.S.supervisor at Jiangnan University.His research interests include image quality assessment and pattern recognition,etc.

桑庆兵（1973—），男，安徽明光人，2013年于江南大学图像处理专业获得博士学位，现为江南大学物联网工程学院副教授、硕士生导师，主要研究领域为图像质量评价，模式识别等。

CHENG Dayu was born in 1989.He is an M.S.candidate at School of Internet of Things Engineering,Jiangnan University.His research interest is image quality evaluation.

程大宇（1989—），男，辽宁丹东人，江南大学物联网工程学院硕士研究生，主要研究领域为图像质量评价。

Blind Image QualityAssessment via Sparse Representation*

SANG Qingbing+,CHENG Dayu
School of Internet of Things Engineering,Jiangnan University,Wuxi,Jiangsu 214122,China
+Corresponding author:E-mail:danyeerchen@yahoo.com

Existing blind image quality assessment(BIQA)algorithms usually build a mapping model by support vector regression(SVR)or neural network.These algorithms need a large number of samples;they are weak in generalization(perform well when training and testing on the same database,but poorly on different one).In order to overcome these deficiencies,this paper proposes a BIQA algorithm based on sparse representation.It utilizes the joint statistics information of gradient magnitude(GM)map and Laplacian of Gaussian(LOG)response and the correlation in the wavelet subbands to compose a feature dictionary,then represents the feature of a test image via sparse coding,finally estimates the differential mean opinion scores(DMOS)of dictionary images and sparse coefficient to get the predicted quality scores.The experimental results on multiple databases show that,compared with other algorithms,the proposed algorithm performs more accurately and stably under low ratio of training samples, and possesses better generalization ability and stability.

blind image quality assessment;sparse representation;statistic feature;wavelet transform

A

：TP391

10.3778/j.issn.1673-9418.1512082

*The National Natural Science Foundation of China under Grant No.61170120(国家自然科学基金);the Prospective Research Project of Jiangsu Province under Grant No.BY2013015-41(江苏省产学研项目).

Received 2015-11,Accepted 2016-01.

CNKI网络优先出版:2016-01-14,http://www.cnki.net/kcms/detail/11.5602.TP.20160114.1658.004.html