自适应预测压缩跟踪

吴腾飞，江艳霞，刘子渊，仲思凯



自适应预测压缩跟踪

吴腾飞，江艳霞，刘子渊，仲思凯

( 上海理工大学光电信息与计算机工程学院自动化系，上海 200093 )

为解决压缩跟踪过快引入跟踪误差和样本采集方面的缺陷，首先，引入基于预测向量的采样搜索策略，通过前两帧跟踪到的目标位置预测后一帧目标的运动方位，并采用扇形区域采样方式缩小有效样本的范围；其次，根据前后两帧跟踪到的目标的对照来判断复杂背景或遮挡的发生，利用Bhattacharyya系数自适应地改变分类器参数更新系数。实验证明，这些策略避免了因压缩跟踪缺陷导致的跟踪失败，改进后的算法比原算法具有更好的鲁棒性和时效性。

压缩跟踪；预测向量；自适应；贝叶斯分类

0 引 言

目标跟踪作为计算机视觉领域的研究分支发展迅速。近年来研究人员提出许多优秀的跟踪算法及相应的特征提取方法，应用较为广泛的有基于滤波理论的目标跟踪方法[1-2]，基于概率理论的目标跟踪方法[3-4]和基于偏微分方程的目标跟踪方法[5-6]。

从信号分解和逼近理论发展起来的压缩跟踪算法[7-12]简单、高效，但是依然存在一些缺陷。经过分析，压缩跟踪在跟踪背景复杂或存在遮挡的情况下，引入过多误差，跟踪稳定性变差；目标搜索窗口设置为固定的圆形区域，搜索空间存在大量的无效样本，尤其是与物体运动方向垂直的边缘附近的样本最为无效，不能准确更新分类器参数，而且影响跟踪速度。针对以上问题，本文提出了自适应预测压缩跟踪算法(VACT)。VACT中引入预测向量，利用前两帧目标所形成的向量来预测下一帧目标的运动方位，对采样区设定半径和搜索角度，使搜索窗口近似扇形区域，减小无效样本的比重，提高目标跟踪的准确性和时效性；引入Bhattacharyya系数[13]改善模板更新策略，改变了原算法根据经验固定更新参数的模式，使其能够自适应地根据目标的变化调整学习因子，减小遮挡、复杂背景等对跟踪的影响。

1 压缩跟踪算法

1.1 压缩跟踪算法简介

压缩跟踪算法建立在如下的条件之上：1) 稀疏随机测量矩阵[14-15]满足有限等距性质[16-17](RIP性质)。2) 经过投影后的低维图像空间服从独立同一分布。3) 提取的低维特征向量服从高斯分布[18]。

压缩跟踪流程如图1所示，将第-1帧中的目标利用压缩感知理论[7-9]经过尺度变换后降维处理，然后对目标、背景对应的正负样本采样并提取Haar-like特征[7]，将样本特征通过贝叶斯分类器判别确定第帧图像中目标的位置，最后更新分类器参数，进而跟踪第+1帧中目标。

图1 压缩跟踪流程图

1.2 压缩跟踪算法的缺陷

目标跟踪过程中样本的采集直接关乎跟踪的准确性和时效性，压缩跟踪算法采样示意如图2所示。图2中为正样本采样半径、为负样本采样半径，<<。从图中可以看出压缩跟踪算法采集的样本中存在很多距离目标位置较远的样本，它们对分类器参数更新是无效的，并且会引入噪声特征，影响后续分类判别的准确性。本文提出的基于预测向量的采样策略降低了这一缺陷的影响，改进后采样示意图如图3所示，通过前两帧生成的预测向量的指引，样本搜索区域明显减小，有效样本比重增大。

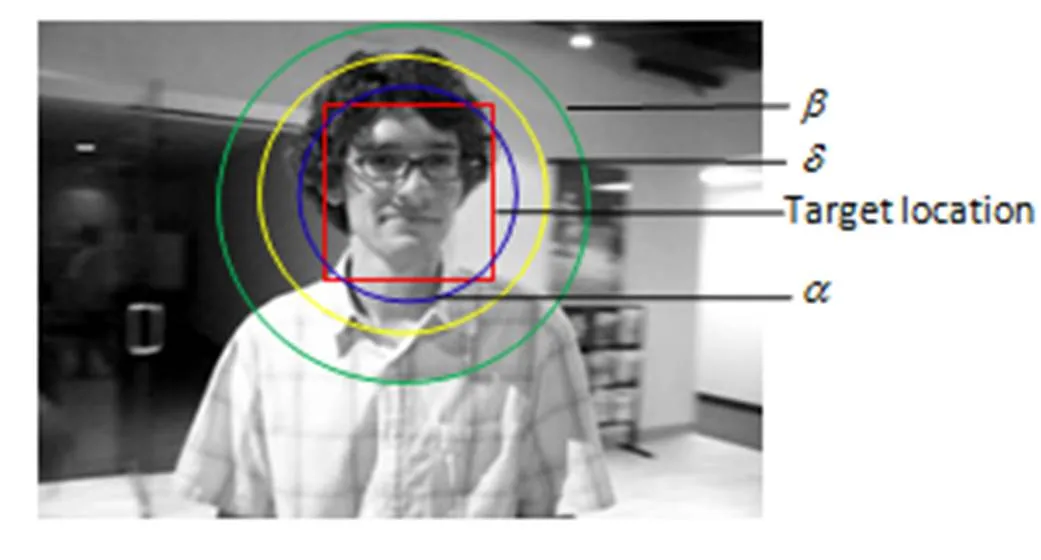
图2 压缩跟踪采样示意图

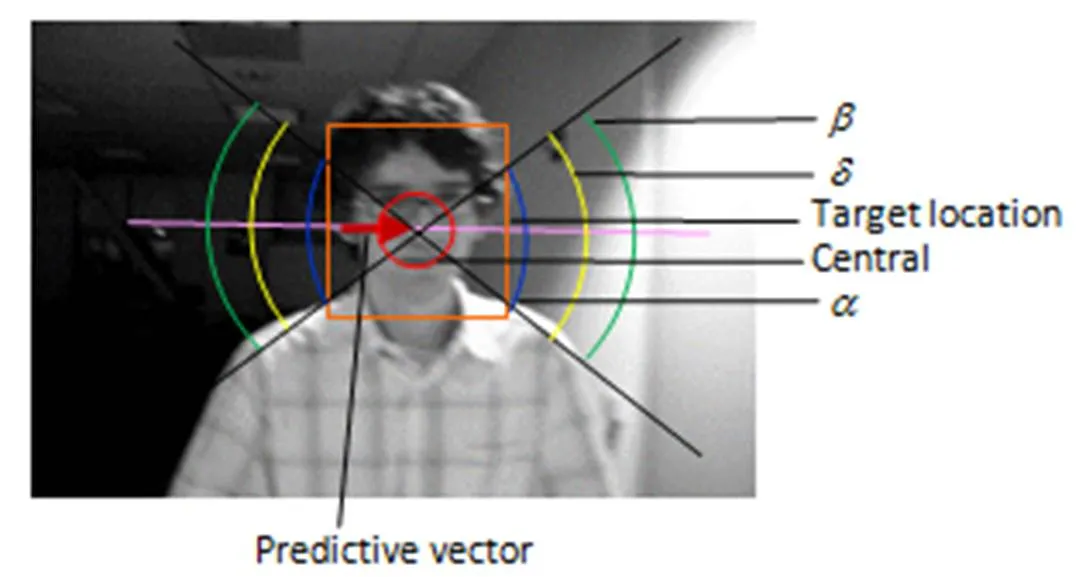
图3 VACT采样示意图

压缩跟踪算法构建对数贝叶斯分类器[7-8]，分类器参数均值和方差通过下式进行更新：

2 自适应预测压缩跟踪

2.1 预测向量

预测向量是根据前两帧目标位置生成，能够指引待跟踪目标的运动方位。视频序列中目标的运动都是连续的，相邻图像间存在对应的时空关系，这种时空关系在数学上就是相邻图像上同一位置的两点之间的连线是近似平滑连续的。基于以上思路定义如下的预测向量和约束角度：

2.2 自适应参数更新

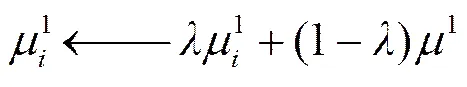
、分别是本次更新的模板参数和上一帧模板参数的差值，将、代入上式得：

由式(1)、式(2)、式(7)可知，模型参数更新由两部分组成：其中一部分是前一帧目标所确定的模型参数，代表目标的稳定性；另一部分是由当前帧图像跟踪点附近样本学习得到的新的模型参数，代表目标的动态性。新旧模型参数通过学习因子线性组合得到更新后的模型参数。在实际运动中会存在不同复杂程度的背景及遮挡等情况，学习因子应当是变化的，引入Bhattacharyya系数(巴氏系数)[13]用于模型参数更新。巴氏系数是两个统计样本重叠量的近似值，源于Bhattacharyya距离(巴氏距离)，用于表征两个离散或连续概率分布的相似性，其公式为，其中，为巴氏系数，0≤≤1，0≤≤∞。由公式可知与为负相关关系，巴氏系数越大，重叠度越高，表明巴氏距离越小，图像和越相似，反之，图像和差别越大。

对于跟踪到的目标，使用归一化直方图作为跟踪目标的辅助表达，计算前一帧和当前帧图像中目标的巴氏系数用于比较前后图像目标间的相似性。新的学习因子定义：

由以上讨论可知，前后两帧目标图像重叠度越高，越接近于1，表明它们越相似，需要对前一帧模型参数较大的学习因子；反之，表明它们相似度小，需要对前一帧模型参数较小的学习因子。

2.3 算法步骤

输入：第1帧、第帧图像中的目标位置

输出：第+1帧图像的目标位置及更新后的模型参数

步骤：

c) 对(b)中图像特征分类判别，确定第+1帧图像的目标位置；

d) 根据式(5)在第+1帧图像目标附近以为半径采集正样本，并提取特征；根据式(6)在第+1帧图像目标附近以为半径采集负样本，并提取特征；

e) 计算第帧和第+1帧目标的巴氏系数，根据式(1)、式(2)、式(8)更新分类器参数。

3 实验及结果分析

为了评估改进后算法的跟踪效果，实验图像库是四个不同复杂程度公开的视频图像序列，它们分别是(a) David图像序列，(b) Girl图像序列，(c) Panda图像序列，(d) Car图像序列。进行对比的算法是快速压缩跟踪算法(FCT)[8]，多例学习跟踪算法(MIL)[19]，TLD跟踪算法(TLD)[20]和粒子跟踪算法(PFT)[21]。实验中，以上算法参数的设置均采用原文中的实验数据。

实验划分两部分：横向对照实验和纵向对照实验。横向对照实验是与原算法(CT)正面直接进行对比，纵向对照实验是与上述四种算法进行对比，侧面对照VACT的跟踪效果。

3.1 实验评判准则

定义跟踪正确率TS(TS)和分数score，，其中R为跟踪到的实际位置窗口，T为理论上的位置窗口。如果某一帧跟踪分数大于0.5，则认为跟踪结果是正确的，正确率TS为所有帧图像中目标跟踪正确的百分比。实验中我们以跟踪时间和跟踪正确率TS作为评判标准。

3.2 实验初始化

基于相同的初始位置与实验环境，环境为：Matlab2014a和Visual C++6.0，Windows7，2GB Intel(R) Core(TM)2 CPU T6500。VACT中正样本采样半径设置为5，负样本采样半径、分别设置为10、17，中心样本区半径设置为3，样本搜索半径设置为18。学习因子初始值设置和CT相同为0.85。

表1 样本搜索角度测试结果

3.3 横向对照实验

采用与文献[7]中相同的视频图像序列—David图像序列，图4所示是对该图像中人脸的跟踪结果。其中以第95、140、185和271帧为代表的图像中目标无遮挡且变化平缓，两种算法对目标的跟踪效果相似，但是VACT的时效性更好(见表2)。而第286、296、388和400帧图像中目标存在手遮挡和眼镜扰动的现象，两种算法跟踪的结果有明显的差异，因为CT在这样的情况下，容易过快引入干扰误差，导致跟踪精度下降；而VACT运用预测向量策略，缩小无效采样范围，减少无效样本的比重，且学习因子可以根据遮挡情况自动地改变大小，能够减轻遮挡、扰动的影响，使跟踪更加准确稳定。经测定，CT在David视频集上跟踪的正确率TS为0.89，VACT跟踪的正确率TS为0.99，改进后算法鲁棒性更好。

在不同帧数下的跟踪时间如表2所示，同一组帧数的跟踪时间试验十次取其平均值。

图4 CT和VACT跟踪结果对比

表2中的数据表明随着帧数的增加，跟踪时间随着增加，CT和VACT的跟踪时间差值逐渐增大，VACT算法基于预测向量扇形区域的采样空间，降低了跟踪目标所需的时间。理论上，按照搜索角度的大小进行计算，VACT跟踪时间是CT时间的九分之四，表2中实际用时与计算值有所差别，原因在于算法中的模型参数更新方法增加了部分计算量，使得没有达到理论值，但是仍然可以看到算法速度得到了改善。

表2 CT和VACT跟踪时间对比

3.4 纵向对照实验

纵向对照实验是采用前面所述的四种算法在四种不同的视频图像序列(共3 121帧)中进行实验，并将CT的跟踪结果一并比较，实验结果如表3、表4和图5所示。

表3 算法跟踪正确率

表4 算法跟踪运行时间

表3、表4中每个图像序列实验值是试验十次平均值，最优结果加粗显示。表3中结果表明本文改进的算法VACT在跟踪精度上有一定优势，在几个典型的图像序列中取得最优或次优的结果。其中在Car图像序列中目标物体运动迅速，存在遮挡和旋转的情况，TLD算法取得较优的跟踪效果，因为它集合了检测、跟踪与机器学习的理论，使得跟踪稳定性较好，但是它需要较大的存储空间和较长的运行时间，由表4可见其跟踪时间远大于VACT。

图5是几种算法在四中图像序列的跟踪结果。其中(a)、(b)、(c)中目标运动和背景变化缓慢，(a)中存在不同程度的遮挡和光照不均的情况，(b)中背景光照不均匀，(c)中存在复杂背景，(d)中目标运动较快。由实验结果可知，VACT、FCT、TLD跟踪较为鲁棒，CT、MIL和PFT在光照不均匀、遮挡等复杂背景时跟踪会发生较大偏移。综合表3、表4可知，VACT跟踪目标所需时间最短，跟踪准确稳定。

图5 算法跟踪结果

4 总 结

本文针对压缩跟踪算法中样本采集搜索区域大且包含过多无效样本的问题，提出了基于预测向量的样本搜索采集方法，此方法能够缩小搜寻目标的范围，将搜索目标的方向集中在感兴趣的位置，降低无效样本的比重，提高模型参数的准确性并降低跟踪时间。引入巴氏系数，根据前后两帧跟踪点位置的图像差异来实时更新模型参数的学习因子，以适应目标的变化，使得算法在存在遮挡、背景复杂等情况下能够抑制误差积累的速度，提高跟踪的准确性和鲁棒性。关于样本搜索角度的选择是一个经验值，而该值对跟踪效果有一定的影响，需要合理地选择该角度。最终实验结果表明，改进后的算法比原算法具有更好的鲁棒性和时效性。

致 谢：

感谢导师和学长的关怀和帮助，感谢实验室同学的帮助，感谢青年基金、沪江基金项目的资助。

[1] 赵欣，王仕成，廖守亿，等. 基于抗差自适应容积卡尔曼滤波的超紧耦合跟踪方法 [J]. 自动化学报，2014，40(11)：2530-2540.

ZHAO Xin，WANG Shicheng，LIAO Shouyi，. An Ultra-tightly Coupled Tracking Method Based on Robust Adaptive Cubature Kalman Filter [J]. Acta Automatica Sinica(S0254-4156)，2014，40(11)：2530-2540.

[2] WANG Baoyun，CHEN Fei，DENG Ping. Online object tracking based on sparse subspace representation [C]// Chinese Control and Decision Conference，Changsha，China，May 31-June 2，2014：3975-3980.

[3] ZHANG Huanqing，YANG Jinlong，GE Hongwei，. An improved GM-PHD Tracker with Track Management for Multiple Target Tracking [C]// International Conference on Control，Automation and Information Sciences (ICCAIS)，Changshu，China，Oct 29-31，2015：185-190.

[4] ZHANG Hongjian，ZHANG Yuewu，YE Bei，. Multi-sensor Multi-target Tracking Based on a Matrix Reformulation of the GM-PHD Filter [C]// The 26th Chinese Control and Decision Conference (CCDC)，Changsha，China，May 31-June 2，2014：2026-2032.

[5] YU Han，WANG Longsheng，YU Yunzhi. A Video Tracking Algorithm for UAV Based on Differential Evolution Particle Filter [C]// Chinese Control Conference (CCC)，Hefei，China，July 25-27，2012：3955-3959.

[6] Bracey S S，Evans K A. Analysis of Tracking Control Designs for a Delay Differential Equation Model used in the Study of Nanoparticle Dosing Strategies [C]// American Control Conference (ACC)，Portland OR，America，June 4-6，2014：353-358.

[7] ZHANG Kaihua，ZHANG Lei，Yang M H. Real-time Compressive Tracking [C]// European Conference on Computer Vision (ECCV)，Florence，Italy，Oct 7-13，2012：864-877.

[8] ZHANG Kaihua，ZHANG Lei，YANG M H. Fast Compressive Tracking [J]. Transactions on Pattern Analysis and Machine Intelligence(S0162-8828)，2014，36(10)：2002-2015.

[9] Donoho D L. Compressed Sensing [J]. Transactions on Information Theory(S0018-9448)，2006，52(4)：1289-1306.

[10] WANG Wenping，XU Yan. Effective Weighted Compressive Tracking [C]// The Seventh International Conference on Image and Graphics，Qingdao，China，July 26-28，2013：353-357.

[11] XU Huazhong，YU Fei. Improved Compressive Tracking in Surveillance Scenes [C]// The Seventh International Conference on Image and Graphics，Qingdao，China，July 26-28，2013：869-873.

[12] WU Jiayun，CHEN Daquan，YI Rui. Real-time Compressive Tracking with Motion Estimation [C]// International Conference on Robotics and Biomimetics，Shenzhen，China，Dec 12-14，2013：2374-2379.

[13] 李良福，冯祖仁，陈卫东，等. 系数基于Bhattacharyya系数的由粗到精的核匹配搜索方法 [J].模式识别与人工智能，2008，21(4)：514-519.

LI Liangfu，FENG Zuren，CHEN Weidong，. A Coarse-to-Fine Searching Method with Kernel Matching Based on Bhattacharyya Coefficients [J]. Pattern Recognition and Artificial Intelligence(S1003-6059)，2008，21(4)：514-519.

[14] ZHANG Lijun，JIN Rong，YANG Tianbao，. Random Projections for Classification：A Recovery Approach [J]. Transactions on Information Theory(S0018-9448)，2014，60(11)：7300-7316.

[15] Kim S，Choi S J. Bilinear Random Projections for Locality-Sensitive Binary Codes [C]// Computer Vision and Pattern Recognition，Boston M A，America，June 7-12，2015：1338-1346.

[16] Candes E J，Tao T. Decoding by Linear Programing [J]. Transactions on Information Theory(S0018-9448)，2005，51(12)：4203-4215.

[17] Achlioptas D. Database Friendly Random Projections Johnson-Lindenstrauss with Binary Coins [J]. Journal of Computer and System Sciences(S0022-0000)，2003，66(4)：671-687.

[18] Diaconis P，Freedman D. Asymptotics of Graphical Projection Pursuit [J]. Annals of Statistics(S0090-5364)，1984，12(3)：793-815.

[19] TIAN Peng. Object Tracking with Online Discriminative Sub-instance Learning [C]// International Congress on Image and Signal Processing(CISP)，Shenyang，China，Oct 14-16，2015：35-40.

[20] Kalal Z，Mikolajczyk K，Matas J. Tracking-Learning-Detection [J]. Transactions on Pattern Analysis and Machine Intelligence(S0162-8828)，2012，34(7)：1409-1422.

[21] Kim I，Awan T W，Soh Y. Background Subtraction-based Multiple Object Tracking Using Particle Filter [C]// International Conference on Systems，Signals and Image Processing，Dubrovnik，Croatia，May 12-15，2014：71-74.

Adaptive and Predictive Compressive Tracking

WU Tengfei，JIANG Yanxia，LIU Ziyuan，ZHONG Sikai

( Department of Automation, School of Optical-Electrical and Computer Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China )

To deal with the defects of Compressive Tracking (CT) in the tracking error and the sample collection, firstly, the predictive vector was introduced to search samples that can direct motion of the target. Then the fan-shaped sampling areas reduced the amount of computation greatly. Furthermore, we could determine complex background or occlusion through comparison of the neighboring target images, and then update the classifier parameters automatically by applying the Bhattacharyya coefficient. Experiment shows that these improvements can avoid the failure of compressive tracking and the adaptive predictive compressive tracking (VACT) is better than the original algorithm (CT) in robustness and speed.

compressive tracking; predictive vector; self-adaptive; Bayes discriminant

1003-501X(2016)12-0092-07

TP391.41

A

10.3969/j.issn.1003-501X.2016.12.015

2016-03-07；

2016-06-16

国家自然科学基金青年基金(61203143)；沪江基金(C14002)资助项目

吴腾飞(1989-)，男(汉族)，河南周口人。硕士研究生，主要研究工作是视频跟踪，图像处理方面。E-mail: wutengfei1409@126.com。