快速RTM成型工艺用环氧树脂化学流变及固化行为研究
2017-01-17徐海兵林新耀涂丽艳祝颖丹
陈 刚,徐海兵,刘 东,林新耀,涂丽艳,祝颖丹,颜 春
(中国科学院宁波材料技术与工程研究所 浙江省机器人与智能制造装备技术重点实验室,浙江 宁波 315201)
快速RTM成型工艺用环氧树脂化学流变及固化行为研究
陈 刚,徐海兵,刘 东,林新耀,涂丽艳,祝颖丹,颜 春
(中国科学院宁波材料技术与工程研究所 浙江省机器人与智能制造装备技术重点实验室,浙江 宁波 315201)
针对快速RTM成型工艺对树脂性能的要求,研究了环氧树脂的化学流变行为和固化行为。根据其流变行为,发现采用双Arrhenius黏度模型方程可以有效预测树脂的成型工艺窗口;根据其固化反应行为,通过Malek方法,确定树脂体系的固化反应为自催化反应,采用Sestak-Berggren双参数自催化动力学模型对其固化行为进行分析,发现模型曲线与实验曲线基本吻合。研究结果为快速RTM成型工艺参数的确定提供技术基础和理论依据。
快速RTM工艺;快速固化环氧树脂;黏度模型;固化动力学模型
0 引言
先进复合材料作为轻量化技术之一,在民用领域的需求与日俱增,而复合材料较高的生产成本也成为制约其大规模应用的瓶颈。快速树脂传递模塑(RTM)技术作为低成本复合材料技术的代表,目前已成为当今复合材料研究领域的热点之一。
在RTM生产过程中,如果不考虑被选树脂的化学特性(如流变性能、固化反应动力学等),则RTM成型用工艺参数(如成型时间、温度、压力等)也就无法准确制定,同样,选择RTM树脂体系时仅考虑树脂基体性能而不考虑其工艺性的做法也是不准确的。
热固性树脂的种类(如酚醛、环氧和双马树脂)将决定最终交联聚合物的热性能、力学性能和耐环境性能。在RTM工艺过程中,制件(模具)尺寸和形状、增强体类型、工艺参数(模具类型、温度、树脂注胶压力、进出胶口分布等)决定着过程的传热速率和传质过程[1]。
采用旋转流变仪研究了环氧树脂的化学流变行为,确定了双Arrhenius黏度模型方程的模型参数。进一步采用差示扫描量热仪研究了环氧树脂的固化行为,同时利用n级反应模型和Sestak-Berggren双参数自催化动力学模型分析了环氧树脂的固化动力学参数。
1 原材料及设备
环氧树脂体系:快速固化环氧树脂EpoTech 167A/B,质量比5∶1,广州博汇提供。
流变仪:Anton Paar GmbH公司的Physica MCR301型旋转式流变仪。
差示扫描量热仪:美国Perkin Elmer Diamond DSC的差示扫描量热仪。
2 热固性树脂的流变模型
2.1 动态黏度测试分析
一般情况下,适合于RTM工艺的树脂黏度应低于1 000 MPa˙s,为了确定RTM注射温度,测试了该树脂黏度-温度曲线,如图1所示。

图1 树脂黏度随温度变化曲线

图2 树脂黏度随时间变化曲线
从图1可知,环氧树脂的黏度随温度的升高而降低,当温度为40 ℃时,树脂黏度为620 MPa˙s,当温度高于55 ℃时,随着温度的升高,树脂的黏度变化趋于平稳。通过树脂体系黏度与温度之间的关系,确定RTM工艺注射温度范围为40~60 ℃。
2.2 等温化学流变模型建立
为了进一步确定准确的温度范围,测试了40、45、50、55和60 ℃下的黏度随时间的变化,如图2所示。树脂黏度随时间的延长而逐渐增大;随着温度不断升高,树脂黏度随时间的增加越来越快,说明树脂体系的固化反应速率越来越快。因此,可以根据所成型制件的尺寸,确定合适的注射温度,以提高工作效率。
根据双Arrhenius 黏度模型方程[2]:

式中,ηt为树脂在t时刻的黏度;η0为树脂在起始时刻的黏度;n为模型参数;t为保温时间。
树脂起始黏度η0和模型参数n之间也符合Arrhenius黏度模型方程,即:

式⑵和⑶中,k1、k2、k3和k4分别是流变模型参数。
由lnη0对1/T作图可得图3。
从图3可以看出,lnη0与1/T的线性关系切合较好,若对lnη0对1/T曲线进一步线性分析,可得:
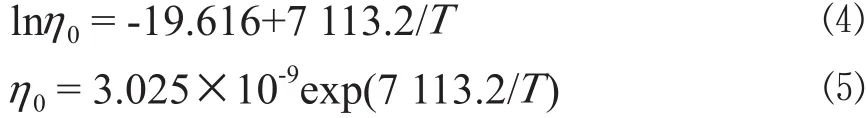
定义ηt/η0为树脂相对黏度,并将该树脂的相对黏度与时间关系作图,如图4所示。
将上述相对黏度与时间的关系进行非线性最小方差分析,然后通过拟合得到不同温度下的模型参数n值,具体见表1。
按上表对lnn与1/T作关系图,如图5所示。
从上图5可知,树脂黏度lnn与时间1/T具有较好的线性关系,表明上述流变模型对所选树脂体系具有较为可靠的拟合关系。线性拟合lnn与1/T关系曲线,可以得到参数值k3、k4,从而可进一步得到模型参数n的表达式:

图3 树脂初始黏度模型参数

图4 不同温度下相对黏度与时间变化曲线

表1 模型参数(n)值

把式⑹代入式⑴,得到该环氧树脂体系的等温相对黏度模型:
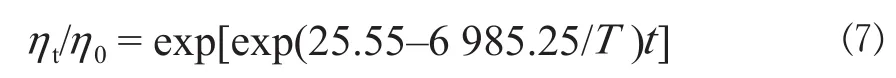
若将式⑺与式⑹结合,便可得该环氧体系黏度计算数学模型:

根据式⑻积分模型方程,可以方便地计算出给定工艺条件(温度对时间的变化条件)下黏度的变化,从而可以对生产过程中不同温度下环氧树脂的黏度进行准确预测,给出快速RTM工艺过程中的树脂注胶温度、模具温度、注胶黏度、注胶时间等。
3 非等温DSC法研究环氧树脂固化反应动力学[3~4]
3.1 n级反应模型
f (α) = (1– α)n⑼其中,n为反应级数。
Kissinger方程:

Crane方程:

其中,β为升温速率,A为指前因子,Eα为表观活化能,R为气体常数,n为反应级数,Tp为DSC曲线峰顶温度。
当Eα/nR远大于2Tp时,Crane方程变为如下:
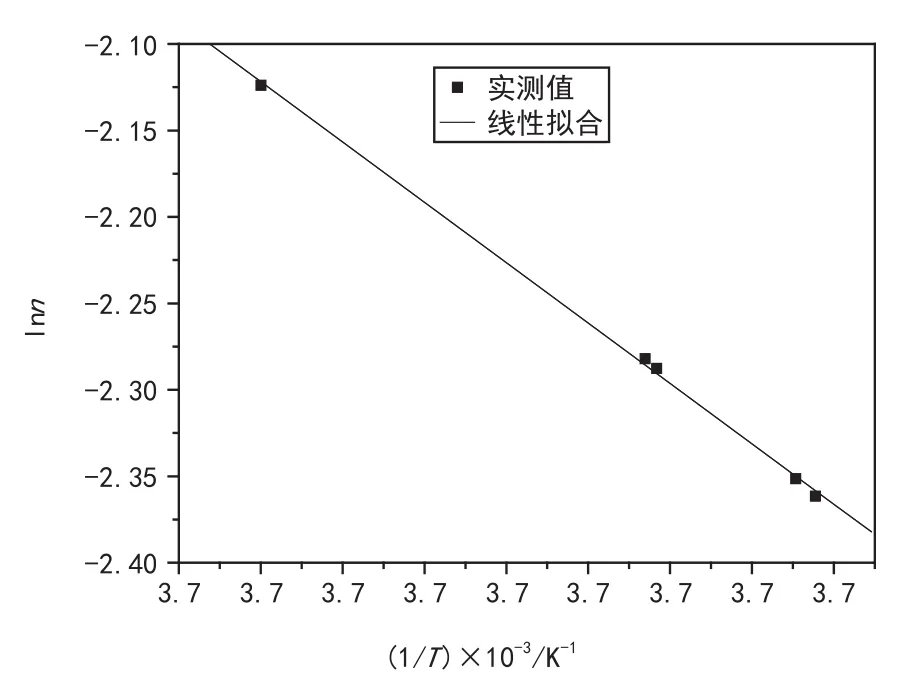
图5 初始黏度与温度关系曲线

扫描不同升温速率下的DSC,根据式⑿对ln(β/Tp
2)–1/Tp作图,得出直线斜率-Eα/R,截距ln(AR/Eα)。最后将求得的Eα代入方程⑾,同时对lnβ–1/Tp关系作图,并经线性拟合后得出直线斜率-Eα/nR,求得n。
环氧树脂EpoTech 167A/167B在2.5、5、10和15 ℃/min升温速率下的非等温固化DSC曲线见图6,热力学数据列于表2。
从图6可知,放热峰的峰始温度Ti、峰顶温度Tp、峰终温度Tf均随着升温速率的不断增大而不断升高,同时,放热曲线z逐渐向右移动,放热焓也逐渐增加。
从图7可得:直线斜率-Eα/R = -7 611.24,截距ln(AR/Eα)= 9.87,计算得到Eα为63.30 kJ/ mol,A为13.27×107s-1。
从图8可得:直线斜率-Eα/nR = -8 369.2,结合已知的Eα,可求得n为0.902。
由此,可得该环氧树脂体系的n级动力学模型为:
dα/dt = Aexp(-7 611.24/T)(1– α)0.9⒀从图9可以看出,模型曲线与实验曲线存在较大偏差[6],该树脂体系伴有自催化的固化反应,则不能用简单的n级反应模型来准确地描述该固化反应的过程。

图6 不同升温速率下的DSC曲线
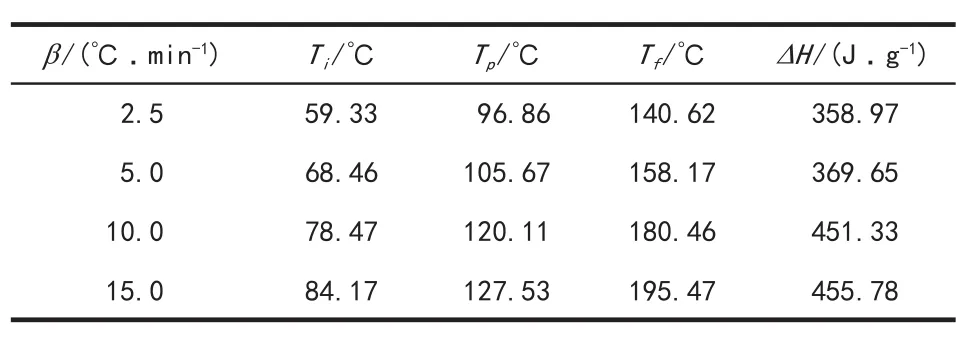
表2 不同升温速率下的DSC扫描结果

图7 ln与1/Tp的关系曲线

图8 ln β与1/Tp的关系曲线

图9 n级模型曲线与实验曲线
3.2 Malek等转化率法
Malek等转化率(等固化度)法[9]如下式:
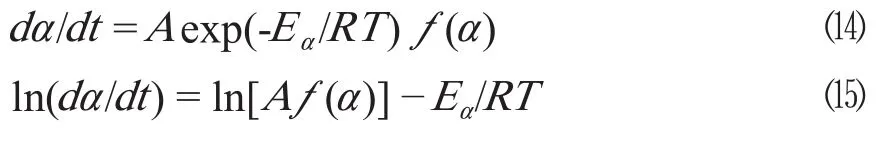
式中,α是固化反应程度,即树脂体系在某一温度时的固化度。
若取固化度0.2、0.4、0.6、0.8,对ln(dα/dt)–1/T作图,如图10所示。
等转化率下的活化能Eα与α的关系如图11所示。
从图11可知,活化能随着转化率的不断提高而略有下降,活化能平均值为49 505.39 J/mol。
在应用Malek等转化率法时,需引入两个特殊的方程y(α)和z(α)[9~10]:

其中,x是Eα/RT,T是绝对温度,π(x)是温度积分的表达式。
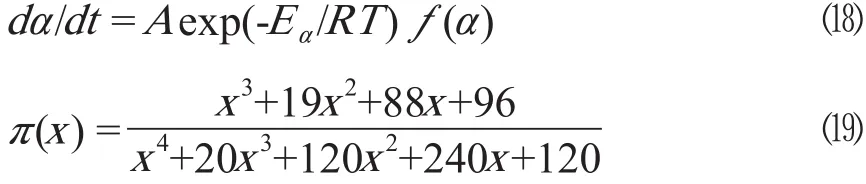
计算y(α)和z(α),并归一化,然后分别对其固化度α作曲线,得出如图12~13和表3。
将y(α)和z(α)的最大值所对应的固化度分别记为αm和则该环氧树脂体系的固化过程可以用双参数自催化动力学模型来表示[11~12]:

由式⒂和⒇可得:

其中αp为DSC曲线中Tp时的固化度。
将上述求得的动力学参数列于下表4,然后得出该环氧树脂体系的固化反应动力学模型如下式:

由图15可知,不同升温速率下,自催化模型曲线与实验曲线基本吻合,该模型在2.5~15 ℃/ min的升温速率范围内均能较好的描述该环氧树脂体系的固化反应过程。

图10 ln(dα/dt)与1/T的关系曲线
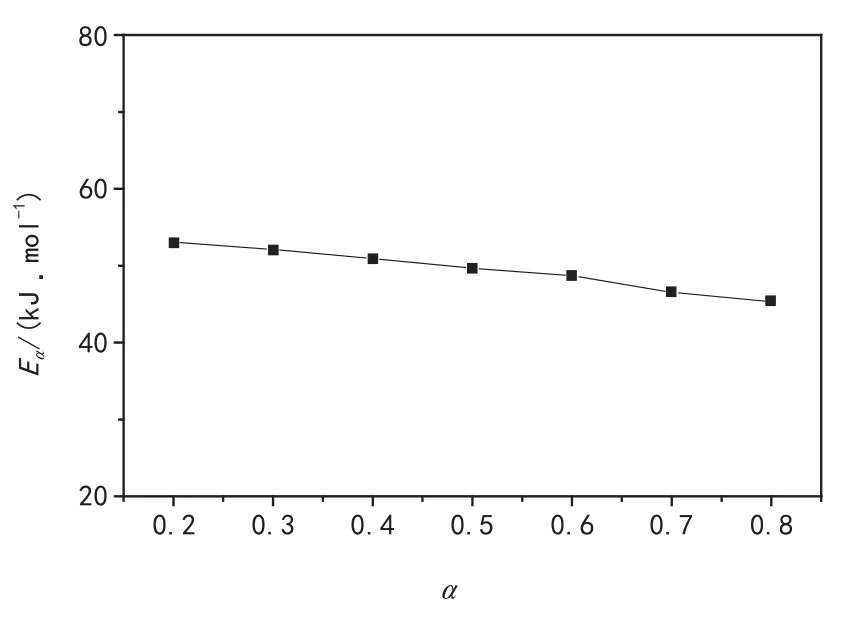
图11 Eα与α之间的关系曲线

图12 y(α)与α的关系曲线
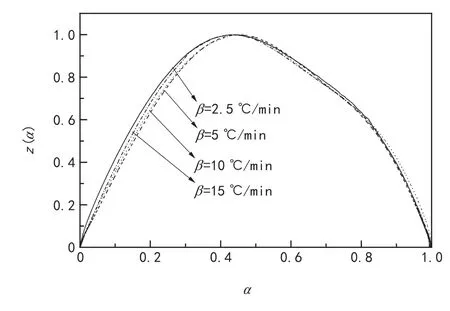
图13 z(α)与α的关系曲线
表3 不同升温速率下的αp、αm和值

表3 不同升温速率下的αp、αm和值
β/(℃˙min-1) αp αm αp∞2.5 0.468 1 0.182 3 0.440 4 5.0 0.430 2 0.174 9 0.465 5 10.0 0.421 1 0.166 0 0.451 0 15.0 0.387 5 0.155 5 0.448 4
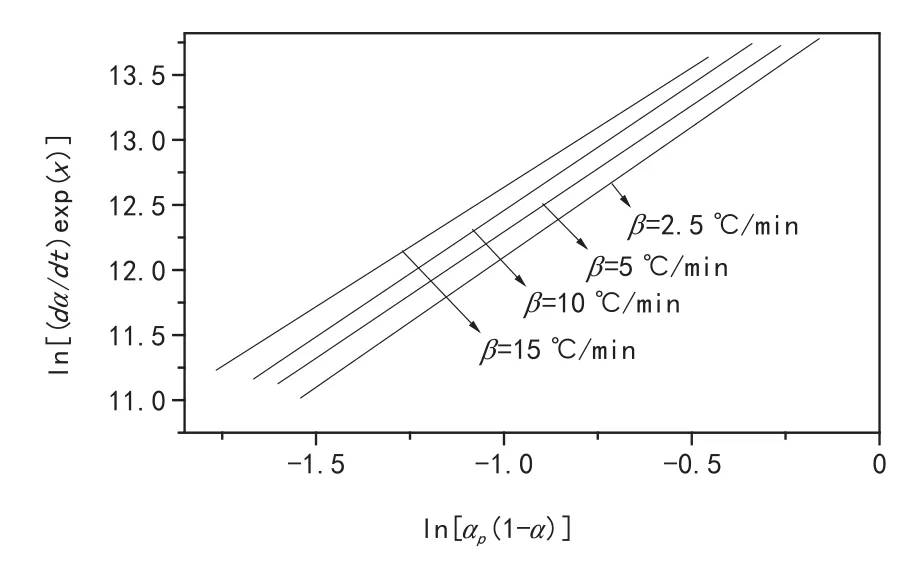
图14 ln[(dα/dt)exp(x)]与ln[αp(1-α)]的关系曲线

表4 该环氧树脂自催化模型动力学参数

图15 自催化模型曲线与不同温度的实验曲线
4 结论
⑴ 建立的黏度计算数学模型可以方便地计算出给定工艺条件(温度对时间的变化条件)下黏度的变化规律,从而对工艺过程中的黏度进行有效地预测并控制。
⑵ 若树脂体系伴有自催化的固化反应,则不能用简单的n级反应模型来准确地描述该固化反应的过程。
⑶ 根据Malek方法,判断树脂体系的固化反应为自催化反应,确定了Sestak-Berggren双参数自催化动力学模型参数,其模型曲线与实验曲线基本吻合。
[1]何天白. 碳纤维复合材料轻量化技术[M]. 北京: 科学出版社, 2015: 226-266.
[2]Wang Q, He T B, Xia P, et al. Cure processing modeling and cure cycle simulation of epoxy-terminated poly(phenylen ether ketone) I: DSC characterization of curing reaction[J]. Journal of Applied Polymer Science, 1997, 66: 789-797.
[3]Wang Q, He T B, Xia P, et al. Cure processing modeling and cure cycle simulation of epoxy-terminated poly(phenylen ether ketone)V: Estimation of temperature distribution during cure process[J]. Polymer Engineering and Science, 1998, 38: 420-428.
[4]卢红斌, 何天白. 聚合物模压成型加工的计算模拟[M]//胡汉杰, 瞿金平. 跨世纪高分子丛书:聚合物成型原理及成型技术: 第15章. 北京: 化学工业出版社, 2000: 301-317.
[5]Kissinger HE. Reaction kinetics in differential thermal analysis[J]. Analytical Chemistry, 1957, 29(11): 1 702-1 706.
[6]Crane LW, Dynes PJ, Kaelble DH. Analysis of curing kinetics in polymer composites[J]. Journal of Polymer Science Part C-Polymer Letters, 1973, 11(8): 533-540.
[7]于伯龄, 姜胶东. 实用热分析[M]. 北京: 纺织工业出版社, 1990: 26-48.
[8]Rosu D, Mustata F, Cascaval CN. Investigation of the curing reactions of some multifunctional epoxy resins using differential scanning calorimetry[J]. Thermochimica Acta, 2001, 370(1-2): 105-110.
[9]Senum GI, Yang RT. Rational approximations of integral of Arrhenius function[J]. Journal of Thermal Analysis, 1977, 11(3): 445-449.
[10]Malek J. Kinetic analysis of crystallization processes in amorphous materials[J]. Thermochimica Acta, 2000, 355(1-2): 239-253.
[11]Sestak J, Berggren G. Study of the kinetics of the mechanism of solid-state reactions at increasing temperatures [J]. Thermochimica Acta, 1971, 3(1): 1-12.
[12]Han K., Lee L J. Dry spot formation and changes in liqid composites molding:1-experimental[J]. Journal of Composites of Composites Materials, 1996, 30(13): 1 458-1 474.
[13]Sestak J, Berggren G. Study of the kinetics of the mechanism of solid-state reactions at increasing temperatures [J]. Thermochimica Acta, 1971, 3(1): 1-12.
Studies on the chemical rheological behavior and curing of epoxy resin in rapid RTM process
CHEN Gang, XU Hai-bing, LIU Dong, LIN Xin-yao, TU Li-yan, ZHU Ying-dan, YAN Chun
( Ningbo Institute of Material Technology and Engineering, Chinese Academy of Sciences, Zhejiang Provincial Key Laboratory of Robotics and Intelligent Manufacturing Equipment Technology, Zhejiang Ningbo 315201 China )
This paper studies on the chemical rheological behavior and curing of epoxy resin in rapid RTM process. According to the rheological behavior, it is found that the resin molding window can be effectively predicted by Arrhenius viscosity-temperature equation. According to the curing behavior, analysis via the Malek-Flynn-Wall-Ozawa method leads to a conclusion that resin curing process is an autocatalytic reaction. By employing Sestak-Berggren two-parameter autocatalytic model in curing analysis, it shows that the theoretical curve coincides well with the experimental data, which provides theoretical and technical support for the parameter optimization in rapid RTM process.
rapid RTM process; fast-curing epoxy resin; viscosity model; curing kinetic model
TQ323.5
A
1007-9815(2016)01-0045-06
定稿日期:2016-02-22
中国科学院科技服务网络计划 (KFJ-EW-STS-080);宁波市重大专项(2014S10004,2015S1004);宁波市自然科学基金(2014A610130);宁波市国际合作项目(2015D10012)
陈刚(1974-),男,青海湟中人,高级工程师,主要从事碳纤维复合材料轻量化技术的研究,(电子信箱) chengang@nimte.ac.cn;通讯作者:颜春,女,博士,高级工程师,研究方向为界面改性及热塑料复合材料研究,(电子信箱)yanchun@nimte.ac.cn。
