下肋U型钢-混凝土组合空腹夹层板的动力特性分析

何 奇，张华刚*，姚 玲，马克俭，李富江，王 越

(1．贵州大学 空间结构研究中心，贵州 贵阳 550003；2．贵州建工监理咨询有限公司，贵州 贵阳 550065；3．黑龙江省建设集团 建筑设计研究院有限公司，黑龙江 哈尔滨 150081)

下肋U型钢-混凝土组合空腹夹层板的动力特性分析

何 奇1，张华刚1*，姚 玲1，马克俭1，李富江2，王 越3

(1．贵州大学 空间结构研究中心，贵州 贵阳 550003；2．贵州建工监理咨询有限公司，贵州 贵阳 550065；3．黑龙江省建设集团 建筑设计研究院有限公司，黑龙江 哈尔滨 150081)

为了解下肋为混凝土外包U型钢的组合空腹夹层板的动力特性，将下肋U型钢按轴向刚度等效为混凝土，采用8节点弹性块体单元应用子空间迭代法求解自振方程计算了50个算例。结果表明：组合空腹夹层板的频率具有密集分布特点，振型与相同支承条件的实心平板类似；支承梁刚度增大有利于提高结构基频，但梁截面高度不宜大于跨度的1/14；基频随楼盖高跨比的提高而增大，结构高跨比可采用1/25～1/20；过大的肋刚度将使结构基频降低，因此肋截面高度可按网格尺寸的1/14～1/8采用；增大下肋U型钢的厚度对提高结构基频是有利的；过小的网格划分频数将降低结构整体刚度，网格长度不宜超过2.5 m；支承条件明显影响楼盖的动力特性，振动舒适度分析时应计及支座刚度影响，提高支座刚度是增大楼盖基频的有效措施。

组合空腹夹层板；动力特性；参数化分析；有限元；大跨度

混凝土空腹夹层板的上、下肋通过剪力键连接而共同工作，当前已成功应用于百多万平方米的实际工程中，具有较好的技术经济指标[1]。张华刚等进行的1/3缩尺板柱-剪力墙结构模型试验表明，水平荷载作用下，空腹夹层板在自身平面内具有无限刚性，竖向荷载作用下，楼盖的受力性能类似于实心平板[2]。空腹夹层板的上、下肋总体可按受力性质划分为受拉肋和受压肋，在贵州铝厂温水游泳馆32 m跨简支屋盖中，为解决受拉下肋混凝土的裂缝控制问题而在短向中部区域的下肋上施加了无粘结预应力[3]，可见受拉肋的裂缝控制是拓展混凝土空腹夹层板跨度的关键问题之一。为此黄勇等提出将下肋改为H型钢而上肋层为混凝土平板的组合空腹楼盖，并在贵阳一中体育馆33 m跨楼盖中成功应用，基频的现场测试结果表明，楼盖具有较好的整体刚度[4]。

混凝土空腹夹层板实际上是通过键连接的双重密肋梁结构，内力分布与空腹网架类似[5]，上肋层薄板对结构强度和刚度贡献较小，马克俭等在此基础上提出了图1所示的下肋U型钢-混凝土组合空腹夹层板结构[6]，U型钢通过栓钉等抗剪连接件与下肋混凝土共同工作，既是下肋混凝土浇筑的模板，又主要承担了下肋的拉(或压)应力，U型钢在下肋节点处通过高强螺栓相互连接，现场基本无焊接工作量，目前已在多个工程中得到应用[7]，施工速度优于混凝土空腹夹层板，在黑龙江中医药大学多层文体中心工程中用作楼盖时，跨度已达39 m[8]，有效拓展了空腹夹层板的使用跨度。

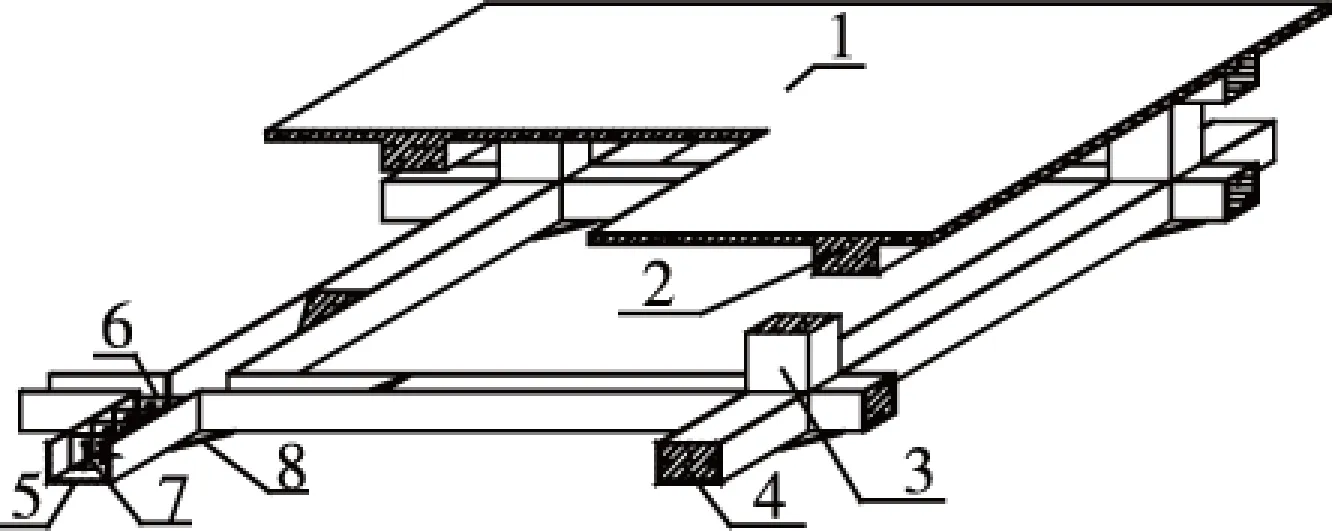
1-表层混凝土薄板；2-混凝土上肋；3-混凝土剪力键；4-下肋混凝土； 5-下肋U型钢；6-下肋焊接箍筋；7-栓钉抗剪连接件；8-下肋节点板。图1 下肋U型钢-混凝土组合空腹夹层板

下肋外包U型钢后，由于钢材弹性模量远大于混凝土弹性模量而使下肋刚度得以加强，虽然当前已有地区规程指导U型钢-混凝土组合空腹夹层板的工程应用[9]，但对这种新型楼盖力学性能研究的文献仍然较少。胡岚等利用环境随机激励实测了楼盖的舒适度指标，表明楼盖具有较好的整体刚度，满足舒适度使用要求[10]；吴帮等对组合空腹夹层板开展了在多遇地震作用下的抗震性能分析[11]。

结构动力特性分析是振动舒适度计算及抗震设计的基础，也是了解结构整体刚度分布特征的重要途径。本文采用8节点弹性块体有限元方法对下肋U型钢-混凝土组合空腹夹层板进行自由振动分析，并在此基础上考虑边梁、结构高跨比、肋刚度、U型钢板厚度、平面网格划分频数和支承条件等因素影响进行参数化分析，借此总结结构的动力特性，以期为工程应用提供参考。

1 分析理论

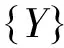
(1)

(2)

欲使上式有非零解，应有：

(3)

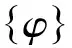
2 结构动力特性分析

2.1 基本算例

本文基本算例情况如图2所示，结构平面尺寸为18 m×18 m，网格尺寸a×b=2 m×2 m，组合空腹夹层板总厚度h=0.75 m，上、下肋的混凝土截面高度均为h1=0.15 m，支承梁(框架梁)截面高度hL=0.9 m，上、下肋及框架梁的截面宽度均为0.4 m，下肋U型钢板厚为4 mm，表层混凝土薄板厚度为60 mm。图2(c)中，h2为剪力键的净高度。混凝土弹性模量Ec=3×104N/mm2，泊松比ν=0.2。钢材的弹性模量Es=2.06×104N/mm2，泊松比ν=0.3。

采用8节点弹性块体单元建立有限元模型时，下肋U型钢截面As按轴向刚度相等原则折算为混凝土截面积Ac[1]：

(4)

将折算混凝土截面与原下肋等高对称增补在下肋截面两侧，增补的宽度为：

(5)

下肋等效处理如图2(c)所示，这是本文对计算模型所做的唯一简化。

考虑外加恒载为2.0 kN/m2，结构自重按网格折算为均布荷载，分项系数取1.2；活载为3.5 kN/m2，组合值系数取0.5，分项系数为1.4。上述荷载可涵盖公共建筑的使用荷载。将荷载设计值折算为标准值后再通过质量单元施加在计算模型上，质量单元均位于楼盖表面，在网格平面上的位置如图2(b)所示，肋边线与框架梁相交处也定位4个质量单元。楼盖四角框架梁相交范围内节点均作线位移约束，以模拟点支承。

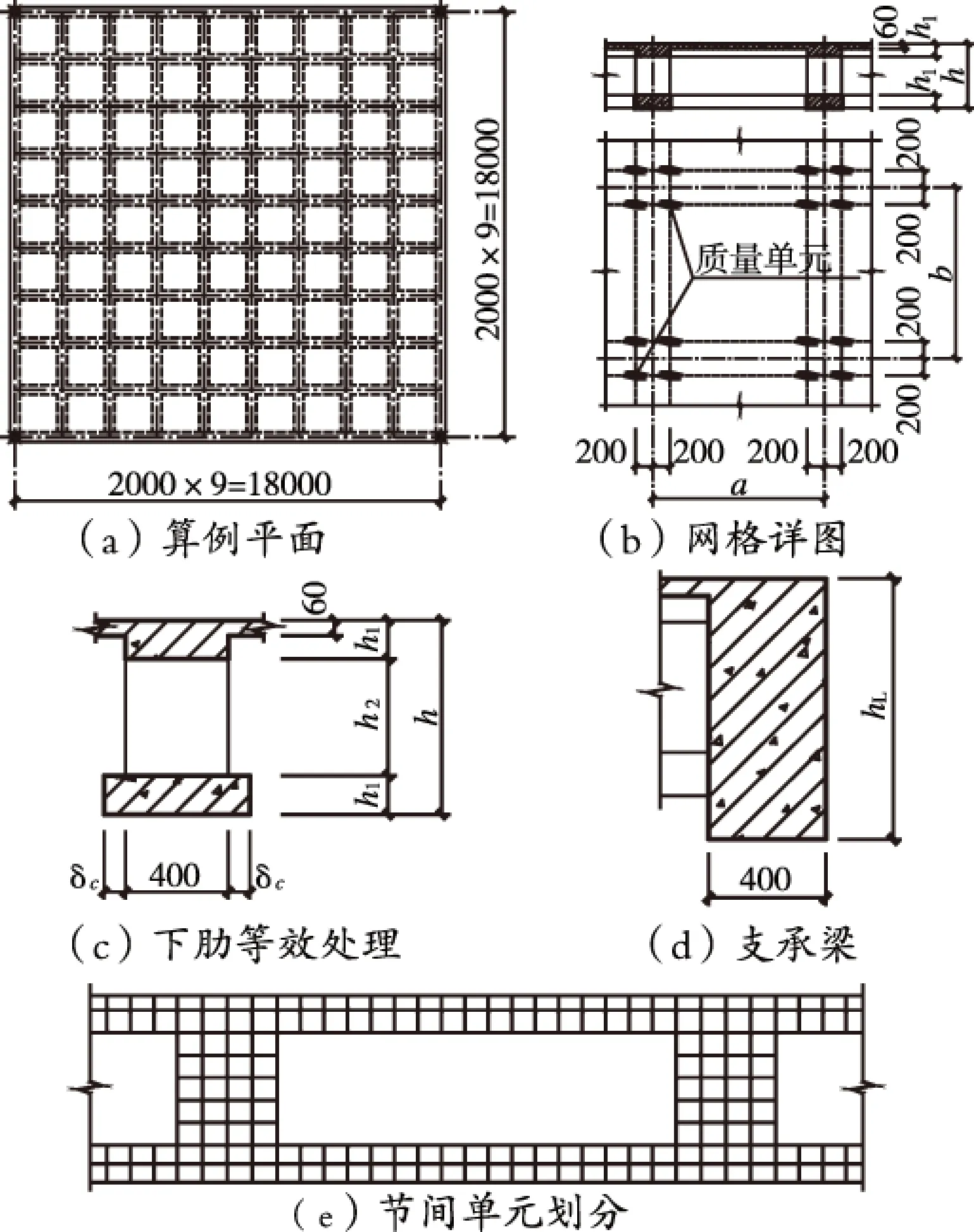
图2 基本算例情况

2.2 计算结果及分析

结构前50阶频率分布如图3所示，前10阶自振频率的数值结果如表1所示。

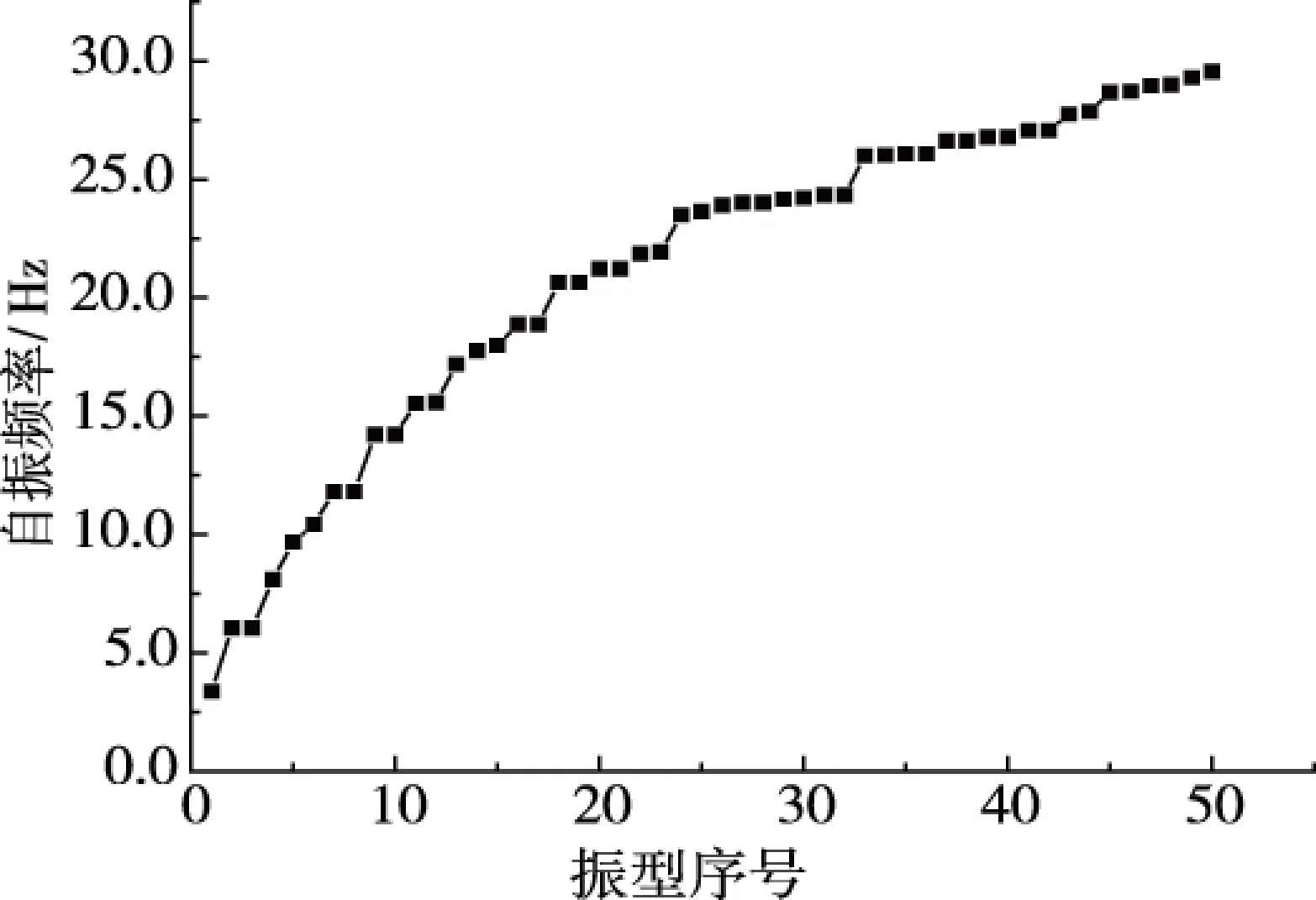
图3 基本算例前50阶自振频率

振型序号12345678910自振频率/Hz3．386．056．058．119．6810．4311．8111．8114．2214．22

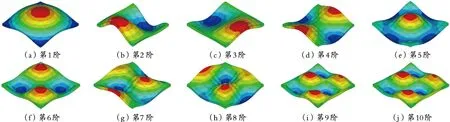
图4 基本算例前10阶振型

如图4所示，结构前10阶振型中，第1阶振型与竖向静载作用下的挠度分布图相似；第2、3阶振型相同，均为全波振型，振动节线为平面对称轴；第4阶振型主要表现为框架梁的振动，并引起组合空腹夹层板出现3个半波振动；从第5阶振型开始出现多波振动。总体而言，基本算例的振型与相同支承条件的实心平板振型类似。

3 动力特性分析的参数化分析

3.1 支承梁刚度对基频的影响

在基本算例基础上通过增大支承梁的截面高度来调整其刚度，以此考察支承梁刚度对组合空腹夹层板基频的影响。此处还计算了hL=0.75 m的算例，支承梁截面高度与组合空腹夹层板厚度相同时，组合空腹夹层板相当于无梁楼盖，在此基础上hL按0.2 m级差由0.9 m渐次增大至1.9 m，支承梁的跨高比约为1/20～1/9，可涵盖实际工程的常用跨高比。7个算例的基频结果如图5所示。

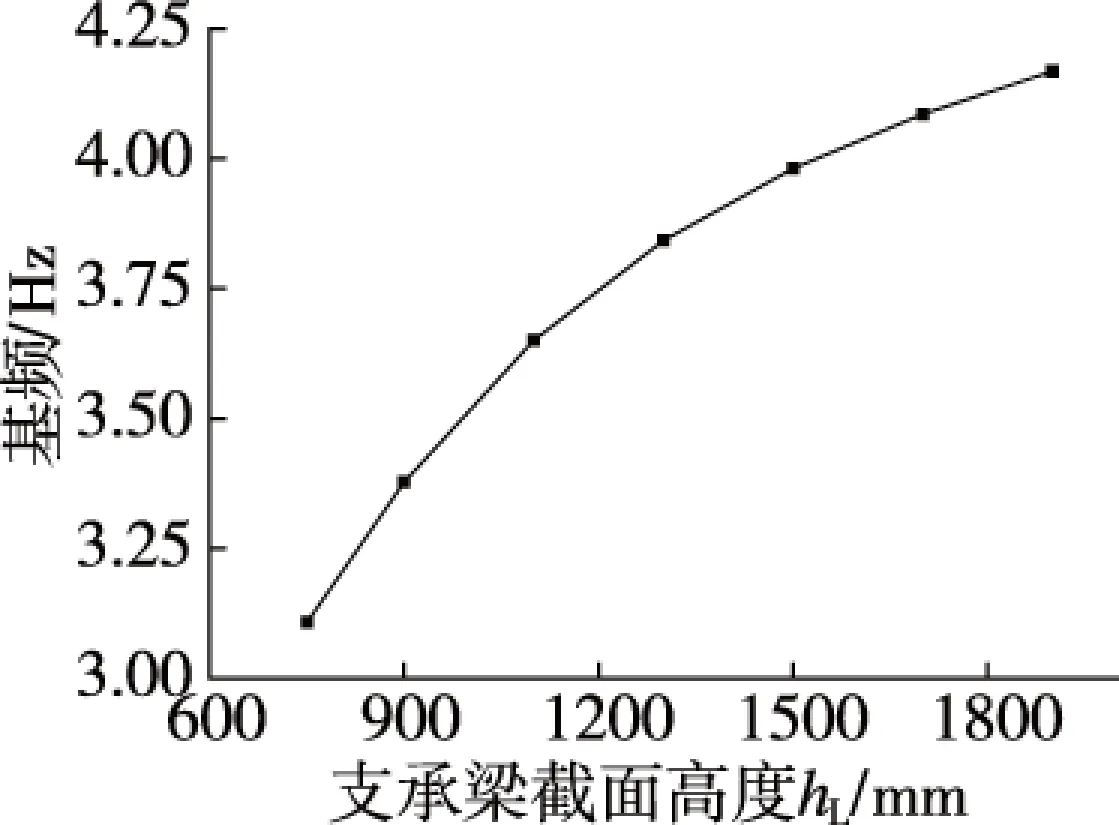
图5 支承梁截面高度对基频的影响

当算例为无梁楼盖时，基频为3.11 Hz，当支承梁截面高度hL=0.9 m时，基频为3.38 Hz，增大了8.7%，因此支承梁对楼盖刚度有明显影响。当hL=1.9 m时，基频为4.17 Hz，与hL=0.9 m算例相比，基频增大了23.3%，可见提高支承梁刚度，可以有效提高组合空腹夹层板楼盖的整体刚度，但梁截面高度超过跨度的1/14后，基频的增幅明显较缓。

3.2 高跨比对基频的影响

基于基本算例，按级差50 mm渐次调整剪力键净高h2，以此改变结构高跨比计算了9个算例，即组合空腹夹层板总厚度h由0.5 m渐变至0.9 m，结构高跨比约在1/36～1/20之间，各算例的支承梁截面高度hL均比结构厚度h大0.15 m。基频的计算结果如图6所示。

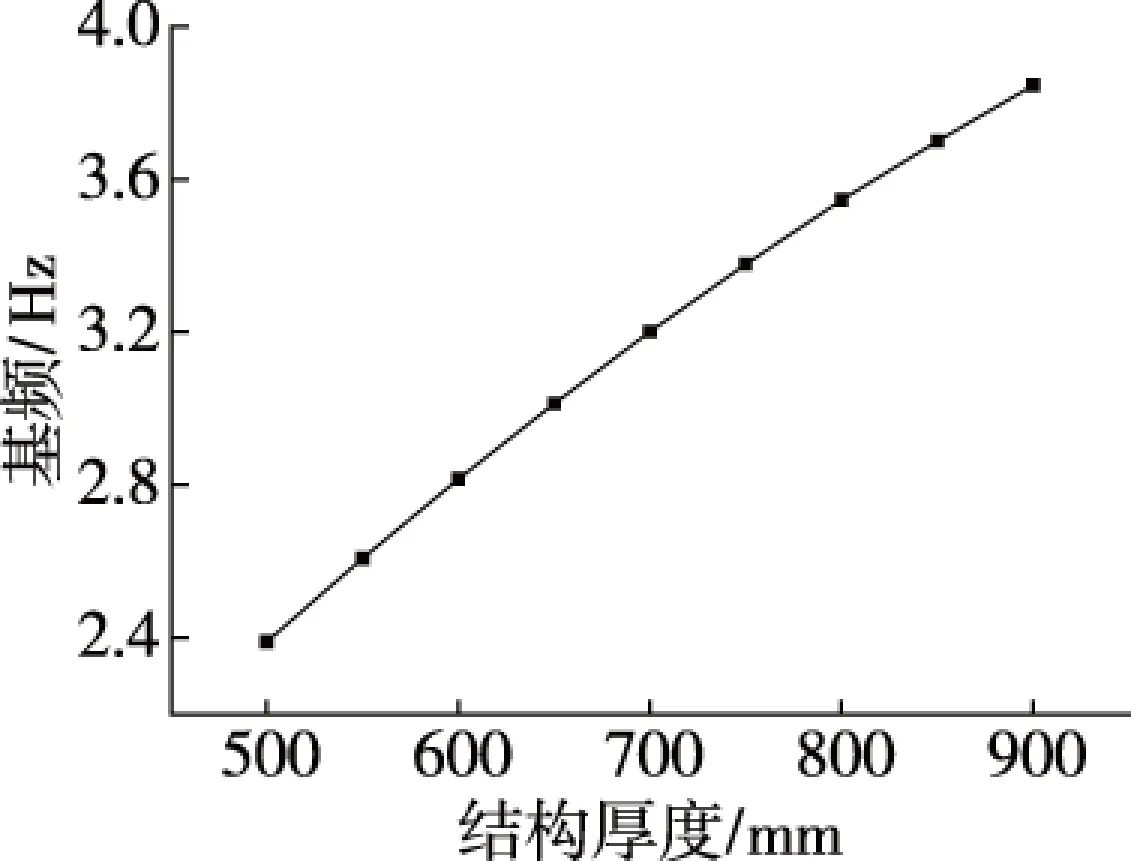
图6 结构厚度对基频的影响

可见，基频随结构高跨比的提高而增大，当结构厚度h=0.5 m时，相当于跨度的1/36，基频计算结果为2.39 Hz，而当h=0.9 m时，相当于跨度的1/20，基频为3.85 Hz，增大了61.1%，因此组合空腹夹层板不宜采用过小的高跨比。

对文献[9]建议的1/25～1/20高跨比范围，此处基频的计算结果在3.38～3.85 Hz，可见对于一般公共建筑，按上述高跨比计算的基频可满足现行规范对舒适度频率指标控制的要求[13]。

3.3 肋刚度的影响

基于基本算例，此处按文献[9]扩大肋截面高度的取值范围进行计算，肋截面高度h1由150 mm按10 mm级差递增至300 mm，相当于按网格尺寸的1/14～1/6确定肋的截面高度，共计算了16个算例，基频计算结果如图7所示。

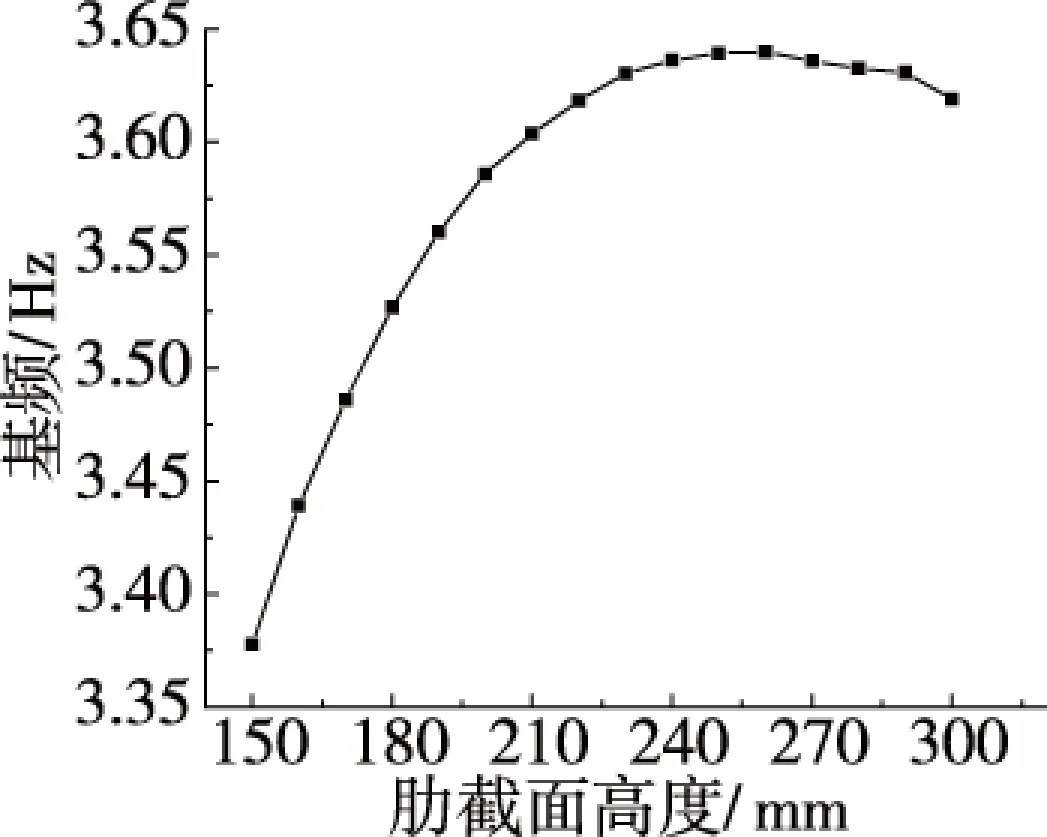
图7 肋截面高度对基频的影响

肋截面高度h1按网格尺寸的1/14～1/8范围确定时，基频随肋截面高度的增加而增加。当h1=150 mm时，基频为3.38 Hz；当h1=260 mm时，基频变为3.64 Hz，增大了7.7%。当h1>260 mm时，肋截面高度反而使基频呈下降趋势，对结构整体刚度的提高并无帮助。因此组合空腹夹层板上、下肋的截面高度可按网格尺寸的1/14～1/8确定。

3.4 下肋U型钢的厚度对基频的影响

在同等混凝土截面条件下，下肋增加U型钢将从构造上增大结构的整体刚度，因此在基本算例基础上考虑U型钢的厚度分别为4 mm、6 mm、8 mm、10 mm和12 mm计算了5个算例，基频计算结果如图8所示。

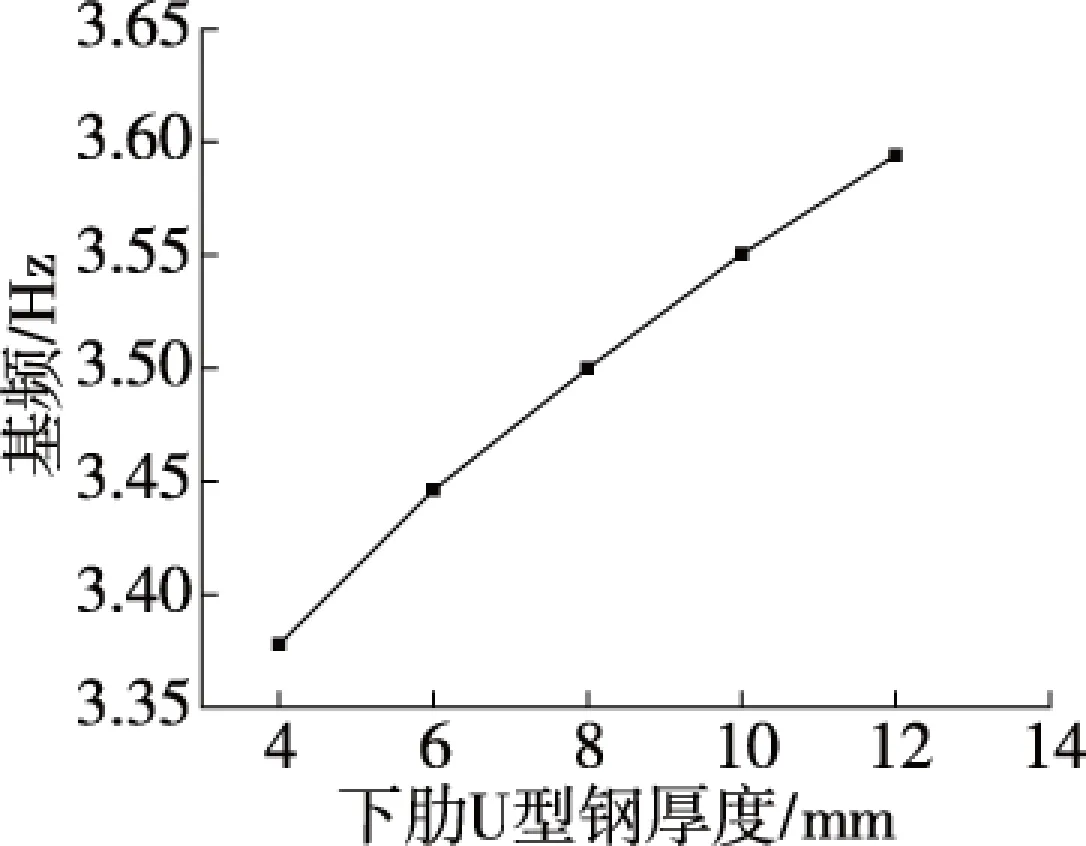
图8 下肋U型钢厚度对基频的影响

可见基频随着下肋U型钢厚度的增加而增加，当U型钢为4 mm厚时，基频为3.38 Hz，而当U型钢厚度增大至12 mm时，基频为3.59 Hz，增大了6.2%。按文献[9]进行工程应用时，往往会根据下肋内力情况加大U型钢的厚度，这对提高结构整体刚度是有利的。

3.5 网格划分频数对基频的影响

在基本算例基础上改变楼盖网格划分频数n计算了5个算例，n分别为6、8、9、10和12，对应网格尺寸分别为3.0 m、2.25 m、2.0 m、1.8 m和1.5 m，基频计算结果如图9所示。

基频随网格划分频数的降低而降低，当网格尺寸为1.5 m时，基频数值为3.71 Hz，网格尺寸加大至3.0 m时，基频为2.65 Hz，降低了28.6%。

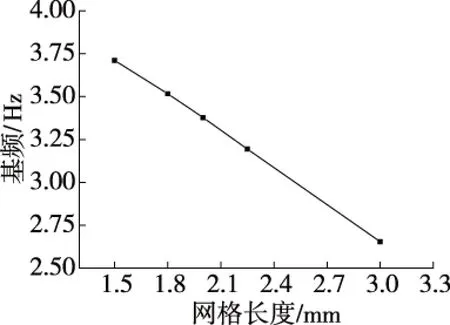
图9 网格尺寸对基频的影响

空腹夹层板的整体刚度主要由肋提供，一般要求网格划分频数不低于5，否则容易使肋刚度降低而削弱楼盖的整体刚度[1]。综合静力性能的分析结果[5]，建议组合空腹夹层板网格划分时，其尺寸不宜大于2.5 m。

4 支承条件对动力特性的影响

前述算例的点支承是结构的理想支承条件，当组合空腹夹层板支承于砌体上，可认为楼盖为简支，当其与钢筋混凝土墙整浇时，可认为支承条件为固支，而柱支承是组合空腹夹层板常见的支承条件。支座刚度的改变将影响楼盖的动力特性，因此将基本算例的支承条件由点支承分别改为柱支承、简支和固支进行计算，以了解支座刚度对楼盖动力特性的影响。

4.1 支承条件对基频的影响

上述四种支承条件下，组合空腹夹层板的基频计算结果如表2所示，其中柱支承时的柱计算长度为4.2 m，横截面尺寸为0.45 m×0.45 m，柱相应的侧向弹簧刚度为4.151×103N/mm。可见4种支承情况下，由于柱侧向刚度的影响而导致楼盖基频最小，而固支支座刚度最大，对楼盖的约束能力最强。因此将组合空腹夹层板用于实际工程而进行舒适度分析时，应计及支座刚度的影响[14]，否则将高估频率控制指标。

表2 支承条件对基频的影响

鉴于柱刚度对结构基频有明显影响，基于柱的计算长度不变，通过将柱截面尺寸由0.45 m×0.45 m以0.1 m为级差增大至1.35 m×1.35 m，基频的计算结果如图10所示。当柱截面尺寸超过0.95 m×0.95 m，即弹簧刚度超过82.5×103N/mm后，基频增长的梯度明显变缓，此时过大的柱弹簧刚度对楼盖整体刚度的提高并无明显帮助。

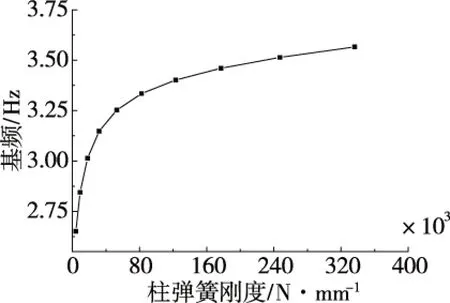
图10 柱刚度对基频的影响

4.2 支承条件对振型的影响

固支条件和简支条件的振型相似，本文将这两种支承条件统称为周边支承，其前10阶振型如图11所示。柱支承的前10阶振型如图12所示。

可见支承条件对振型有明显影响。与点支承相比，周边支承的前3阶振型相似，对于第4阶以后的振型，由于在点支承条件下支承梁的刚度影响而使振型开始差异于周边支承；柱支承条件下柱刚度对振型的影响是显著的，第1阶振型与点支承类似，由于第2、3阶为平动振型，第4阶为扭转振型，因此柱支承的振型与点支承振型相比相当于被推迟了3阶出现。可见组合空腹夹层板楼盖的抗震分析应计及支座刚度影响，特别是柱支承不宜简化为点支承分析。

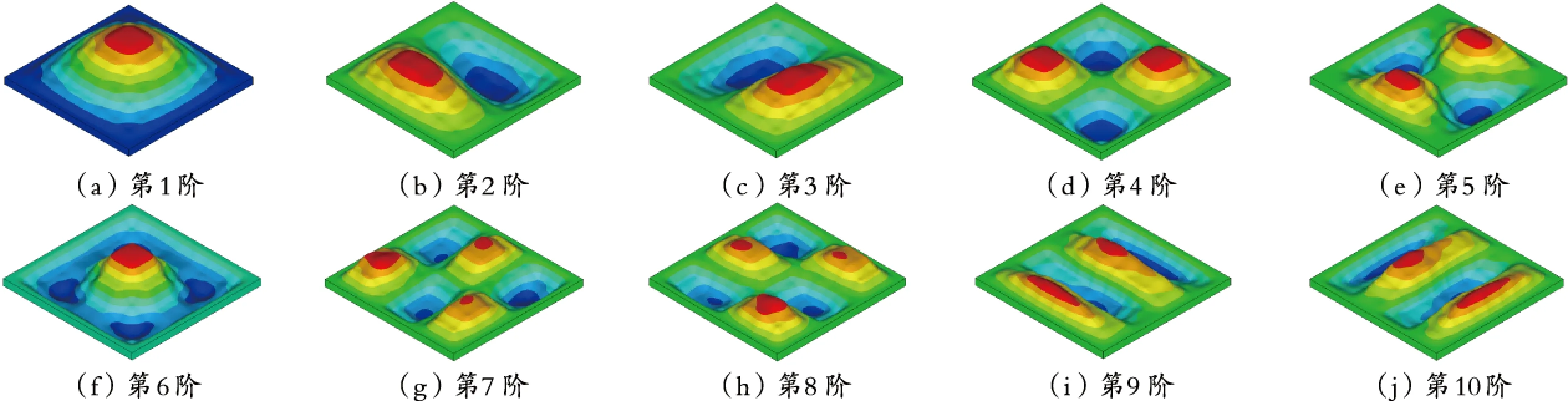
图11 周边支承的前10阶振型

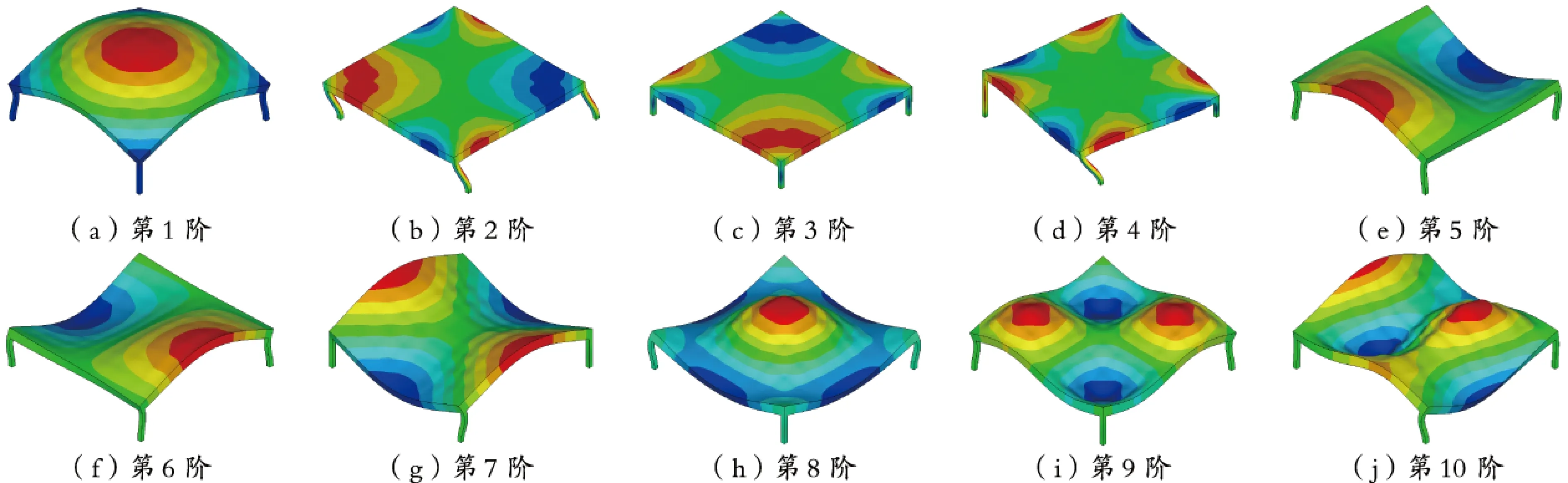
图12 柱支承的前10阶振型

5 结论

(1)下肋U型钢-混凝土组合空腹夹层板的频率分布具有密集性特点，振型与相同支承条件的实心平板类似。

(2)支承梁刚度对楼盖整体刚度有明显影响，提高支承梁刚度可有效提高楼盖的整体刚度，建议梁截面高度不宜超过跨度的1/14。

(3)基频是楼盖舒适度要求的重要控制指标，对于一般公共建筑，组合空腹夹层板的高跨比可取1/25～1/20。

(4)组合空腹夹层板上、下肋的截面高度可按网格尺寸的1/14～1/8确定，过大的肋刚度对楼盖整体刚度的贡献不大。

(5)增大下肋U型钢的厚度有利于提高结构的整体刚度。

(6)一般情况下，组合空腹夹层板的网格划分频数不宜低于5，过低的网格频数将降低楼盖整体刚度，建议网格尺寸不宜大于2.5 m。

(7)楼盖振动舒适度分析应考虑支座刚度影响，否则会高估频率控制指标，增加支座刚度是提高组合空腹夹层板基频的有效途径，结构动力响应分析时不宜将柱支承简化为点支承。

[1] 马克俭，张华刚，郑涛．新型建筑空间网格结构理论与实践[M]．北京：人民交通出版社，2006．

[2] 张华刚，马克俭，黄勇，等．钢筋混凝土空腹夹层板柱-剪力墙结构性能的试验研究[J]．建筑结构学报，2000，21(6)：24-33．

[3] 马克俭，张华刚，黄勇，等．大跨度钢筋混凝土空腹夹层板柱结构的研究与应用[J]．建筑结构学报，2000，21(6)：16-23．

[4] 黄勇，宋佳，段渝忠．33 m跨组合空腹楼盖设计及测试[J]．建筑结构学报，2006，27(2)：88-93．

[5] 张华刚，胡岚，马克俭，等．空腹夹层板的静力性能及其实用计算方法[J]．贵州工业大学学报(自然科学版)，2006，35(3)：82-87．

[6] 马克俭，张华刚，肖建春．贵州工业大学空间结构的理论与实践[J]．贵州工业大学学报(自然科学版)，2002，31(6)：1-9，62．

[7] 王其明，李晨，陈志华，等．苏州重元寺大禅堂钢-混凝土组合空腹夹层板屋盖设计[J]．建筑结构，2015，45(2)：25-28．

[8] 胡岚，马克俭．U形钢板-混凝土高强螺栓连接组合空腹夹层板楼盖结构研究与应用[J]．建筑结构学报，2012，33(7)：61-69．

[9] DB 23/T 1539-2014，钢筋混凝土空间网格结构空腹夹层板楼盖技术规程[S]．哈尔滨：黑龙江省住房和城乡建设厅，2014．

[10] 胡岚，马克俭，易伟建，等．U形钢板-混凝土高强螺栓连接组合空腹夹层板楼盖舒适度实测与研究[J]．建筑结构学报，2012，33(5)：70-75．

[11] 吴帮，申波，马克俭，等．U形钢板-混凝土组合空腹夹层板在多遇地震作用下的抗震性能分析[J]．贵州大学学报(自然科学版)，2016，33(2)：117-122．

[12] 包世华．结构动力学[M]．武汉：武汉理工大学出版社，2005．

[13] JGJ3-2010，高层建筑混凝土结构技术规程[S]．北京：中国建筑工业出版社，2011．

[14] 姜岚，张华刚．大跨度空腹夹层板楼盖基于舒适度要求的动力特性分析[J]．空间结构，2014，20(3)：56-60，81．

(责任编辑：周晓南)

Dynamic Characteristics Analysis of Open- web Sandwich Plate of U- shaped Steel- concrete Composite on Bottom Ribs

HE Qi1,ZHANG Huagang1*,YAO Ling1,MA Kejian1,LI Fujiang2,WANG Yue3

(1．Research Center of Space Structure，Guizhou University，Guiyang 550003，China；2．Guizhou Construction Supervision & Consulting Co．Ltd，Guiyang 550065，China；3．Heilongjiang Building Engineering Architectural Design & Research Institute Co．Ltd， Harbin 150081, China)

In order to study dynamic characteristics of open- web sandwich plate of U- shaped steel- concrete composite on bottom ribs，the 50 structures whose U- shaped steel of bottom ribs are replaced to concrete by equal axial stiffness were calculated according to 8 node elastic block element and subspace iteration method．The results show that mode of composite open- web sandwich plate are similar with plate under same supporting conditions，and its frequency is of dense distribution．Its supporting beam section height should not be greater than its span of 1/14，while improving stiffness of supporting beams is beneficial to increasing structure frequency．The fundamental frequency increases along with the improving of structure height- span ratio which could use 1/25～1/20．The ribs section height should use the 1/14～1/8 of the grid size，because larger rib stiffness will reduce the structural fundamental frequency．Increasing bottom ribs U- shaped steel thickness is advantageous to improving fundamental frequency．Grid length which is too long to reduce the structural stiffness should not be more than 2.5 m．The measure used for improving bearing stiffness is very effective to increase floor fundamental frequency，and vibration comfort analysis must consider its influence，while the dynamic characteristics of the floor is obviously affected by supporting conditions．

composite open- web sandwich plate; dynamic characteristics; parameter analysis; finite element method; large span

1000-5269(2016)06-0071-06

10.15958/j.cnki.gdxbzrb.2016.06.17

2016-07-26

国家自然科学基金项目资助(50968004)

何奇(1991-)，男，在读硕士，研究方向：新型建筑空间网格结构力学性能，Email：heqi1991@126.com.

*通讯作者： 张华刚，Email：zhg0618@163.com.

TU311.3

A