基于数据挖掘的电子皮带秤皮带跑偏检测

朱 亮，李东波，吴崇友，吴绍锋，袁延强

（1. 农业部南京农业机械化研究所，南京 210094；2. 南京理工大学机械工程学院，南京 210094；3. 南京三埃工控股份有限公司，南京 211100）

基于数据挖掘的电子皮带秤皮带跑偏检测

朱 亮1，李东波2，吴崇友1，吴绍锋2，袁延强3

（1. 农业部南京农业机械化研究所，南京 210094；2. 南京理工大学机械工程学院，南京 210094；3. 南京三埃工控股份有限公司，南京 211100）

为提高电子皮带秤连续累计称量精度，针对严重影响精度的电子皮带秤跑偏，采用对皮带秤现有原始传感器的数据挖掘实现跑偏量实时在线检测，以取代传统硬件检测设备。引入流形学习和深度学习，分别提出了基于局部切空间排列（local tangent space alignment,LTSA）+广义回归神经网络（generalized regression neural networks,GRNN）和基于连续深度置信网络（continuous deep belief networks,CDBN）的在线跑偏特征提取模型，再结合极限学习机（extreme learning machine,ELM）以跑偏特征为模型输入进行跑偏量预测。最后通过试验对该文提出的在线跑偏量预测模型的性能进行了验证：LTSA+GRNN+ELM平均跑偏预测精度为 93.33%，平均每组预测时间 38.29 ms；CDBN+ELM预测精度则高达98.61%，平均每组预测时间1.47 ms。二者预测精度和实时性皆表明能取代传统硬件检测装置，为皮带跑偏检测提供了一种方法，为进一步的皮带秤在线精度补偿和故障预测提供了必要依据。

数据挖掘；传感器；模型；皮带跑偏；流形学习；连续深度置信网络；极限学习机

0 引 言

皮带秤是一种散状物料连续累计称重设备，广泛应用于码头、粮库等各大农作物、工业原料贸易场合。输送带跑偏是皮带秤运行过程中常见的现象，广泛见于各种带式输送机设备核子秤、视觉秤等。造成跑偏的原因很多[1]，但根本原因是输送带张力中心线偏离几何中心线[2-3]。跑偏是一种全局性故障，一旦发生，必定是整条输送带跑偏。输送带跑偏不仅严重影响皮带秤计量精度、稳定性和耐久性，同时也是导致诸如设备主要部件滚筒窜轴、托辊轴承等非正常磨损、输送带撕裂、停机等皮带秤现场事故的主要原因[4]。因此，对跑偏进行实时在线定量检测具有极其重要的意义，所检测到的跑偏量即输送带偏离几何中心线的程度，通常通过输送带边缘与托辊之间距离的变化来定量不仅可用来补偿皮带秤累计计量精度，而且还用来故障预测。

传统输送带跑偏检测分为接触式和非接触式检测：接触式检测主要是采用机械的检测传动轮[4]，通常只能定性检测；非接触式通常采用CCD（charge-coupled device）、PSD（phase-sensitive detetor）[5]、阵列式光电三极管[6]等光敏元器件作为检测传感器，以FPGA（field-programmablegate-array）[7]、DSP（digital signal processor）[8]、ARM（acorn reduced instruction set computer machine）、单片机等为采集处理芯片进行跑偏检测，可实现定量检测。而且，为了能够现场实时监控，两种方式还都需要建立额外的总线通信将跑偏数据实时传送到现场仪表或工控机。毫无疑问，传统检测大大增加了设备制造成本和安装维修成本，不符合制造商和客户的需求。此外，皮带秤的恶劣工作环境使得检测设备难以长期稳定工作，故而需要另觅他径。随着信号处理技术以及数据挖掘技术的日益成熟和广泛应用，对现有传感器数据进行信号处理、数据挖掘、提取输送带跑偏特征以实现输送带跑偏检测是一条可行且可靠的途径。然而，由于皮带秤现有传感器的采样频率大多是在10 Hz以内，进行时频分析后难以获得显著的跑偏特征信号，故只能采用机器学习方法对现有数据进行直接处理。

输送带跑偏时，在称重段输送带上的物料分布会有明显的不一致，输送带跑偏的部分物料会随着输送带做横向运动，并与各部件的振动信息相耦合，单个称重单元数据是难以检测出跑偏，需要对皮带秤多个传感器数据和设备参数数据挖掘才能实现。对于皮带秤的在线输送带跑偏检测，除了检测的准确率外，其实时性更为重要。然而，由于现场传感器的实时数据类别较多、数据之间存在线性或者非线性相关，若采用算法直接对现场传感器数据进行处理必然会消耗大量的计算资源和时间、以致难以满足输送带跑偏检测及特征提取的实时性和准确率。故而，需要优先对现场传感器实时数据的维度进行裁剪，消除部分冗余数据、提取出跑偏特征；然后采用回归分析对特征进行跑偏量预测。由此可见，输送带跑偏检测的准确率和实时性主要取决于降维算法和回归分析模型的性能，其中降维算法尤为关键，算法需尽快地消除足够多的冗余信息、并尽可能地保留有用信息。

在机器学习领域，数据降维的方法有很多，大致可分为传统线性降维算法、流形学习方法以及基于神经网络的降维算法三大类。后两类算法是为了解决传统线性降维算法（主成分分析、多维标度分析等）[9-11]难以处理的非线性相关问题。具有代表性的流形学习算法有距映射算法（isomap）和局部线性嵌入算法（locally linear embedding，LLE）、Hessian LLE、拉普拉斯特征映射算法、局部保留投影算法、局部切空间排列算法（local tangent space alignment，LTSA）、近邻保留嵌入等[12]，基于神经网络的降维算法有受限玻尔兹曼机（restricted boltzmann machine，RBM）、栈式自编码器、深度置信网络（deep belief networks，DBN）、自组织特征映射网络等。针对电子皮带秤跑偏数据存在非线性相关的特性，本文分别结合流形学习和深度学习对电子皮带秤皮带跑偏检测进行研究，分别提出基于LTSA+GRNN+ELM和基于CDBN+ELM的跑偏检测模型，并通过试验将二者与其他模型进行对比验证。

1 基于LTSA的在线皮带跑偏检测

1.1 局部切空间排列算法

流形学习算法已是机器学习领域一个新的研究热点[13]。流形学习最大的优势是更适合揭示数据间非线性相关性结构。LTSA是通过逼近样本空间D={x1,x2,…,xN}中任意一样本点 xi∈D的切空间来构建低维流形的局部几何，再利用局部切空间排列求出整体低维嵌入坐标[14]。LTSA与传统非线性降维方法Kernel PCA本质上是一样的[15]。相较于LLE，具有更好的非线性能力；相较于Isomap，具有更好的实时性。此外，LTSA还具备一定的非线性降噪能力[16]，因此，很适合皮带跑偏特征在线提取，其具体步骤如下：

1）采用最小邻域法构建邻域图G，对于∀xi∈D，其邻域为对其邻域进行中心化处理，计算

3）初始化矩阵B=0，计算矩阵B：

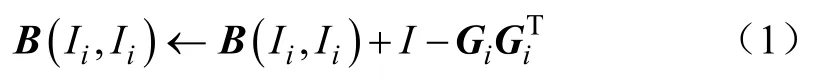
4）除去特征值0对应的特征向量，取矩阵B第2到第d+1最小特征值对应的特征向量u2,…,ud+1，并取样本D降维后的低维数据Y=[u2,…,ud+1]T。

然而，LTSA也存在一些不足，如无法处理新来的样本点，即所谓的“out of sample”问题[17]，无法直接应用于在线输送带跑偏检测。

1.2 基于LTSA+GRNN+ELM的跑偏在线检测

针对“out of sample”问题的解决方法有线性化[18]、核函数化[19-20]、张量化[21-22]等技巧，但最适合在线跑偏检测的是半监督流形学习算法，其思路较为简单清晰：先采用流形学习进行降维，再以降维前后的数据为训练样本构建高维空间到低维流形的显性映射[23-24]。综合考虑，本文采用广义回归神经网络（generalized regression neural networks，GRNN）[25]构建显性非线性映射。

为后续计算的方便、提高后续模型收敛速度，本文先对原始传感器进行归一化处理；其次，采用LTSA对归一化后的数据进行降维处理；再以降维前后的高、低维数据为训练样本采用GRNN进行回归分析建模，构建出高维到低维流形的非线性映射、完成对跑偏特征的提取；最后采用极限学习机（extreme learning machine,ELM）以提取出的跑偏特征（即GRNN的输出）为输入、对应跑偏量为模型输出构建跑偏预测模型。模型如图1a，其构建步骤如图1b。

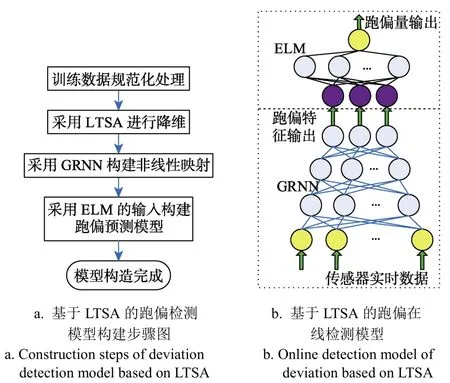
图1 基于LTSA跑偏检测模型示意图及其构建步骤图Fig.1 Schematic diagram and construction steps of online detection model of deviation based on LTSA

2 基于CDBN的在线皮带跑偏检测

2.1 深度置信网络

深度学习（deep learning）是近年来人工智能和机器学习另一个新的研究热点。它区别于SVM（support vector machine）、Boosting、ELM（extreme learning machine）等一系列的浅层学习，专门用于模拟大数据之间的复杂关系，以学习多个表示和抽象层次。传统的浅层学习需要人工地选择特征表达算法[26]，该部分效果的良好与否对最终推断、预测识别的精度起着决定性的作用。而该部分需要依靠大量技巧、经验以及时间，因此，为了能够自动进行特征学习，深度学习应运而生。深度置信网络（DBN）是Hinton于2006年提出深度学习模型[27-28]，其主要思想包括两个：1）更深的网络能够对数据进行更抽象的表示；2）采用先验知识进行无监督预学习，以避免随机初始化权值而导致的局部极值问题。

DBN模型训练为“预训练+微调”：首先采用无监督学习对模型进行“逐层初始化”，然后采用有监督学习对模型进行微调。然而，由于DBN本身是基于RBM（restricted boltzmann machine）的，故DBN不适用于连续数据的降维和特征提取。尽管Hinton提出可将RBM拓展到高斯RBM（gaussian RBM，GRBM）处理连续性数据，但该模型的隐含层输出仍然是二元的[29-30]。针对这一问题，胡昭华等采用CRBM（continuous restricted boltzmann machine）替代RBM，提出了连续自编码网络（continuous auto-encoder network）[31-32]。与PCA等相比，该模型能够发现高维数据的非线性相关关系；与大多数流形学习方法相比，该模型能够直接给出高维数据点到低维空间的显性非线性映射。然该模型缺乏反向监督学习，因此，本节采用CRBM结合反向监督微调和dropout技术[33]构建连续深度置信网络（continuous deep belief networks，CDBN），并将其应用于皮带秤输送带跑偏特征提取及跑偏量预测中。

2.2 连续受限玻尔兹曼机CRBM

CRBM是一种RBM的连续性对称扩展，和RBM一样也是一种特殊的马尔科夫随机场，其概率图模型为一个二分图，包括一个可视层和一个隐含层以及它们层间的连接、但层内无连接。记CRBM的可视层和隐含层的节点分别为nh分别为各层的节点数。W为可视层与隐含层之间的连接权值矩阵，为保证模型的稳定，该矩阵为对称矩阵，即Wij=Wji。

为便于处理连续性数据，CRBM对每个神经单元的输入添加一个均值为 0 的高斯噪声，引入一种连续性随机单元替代RBM中的二元随机单元。令sj为神经单元j的输出、{si}为其他神经单元对该单元j的输入，则该连续性随机单元数学模型为：

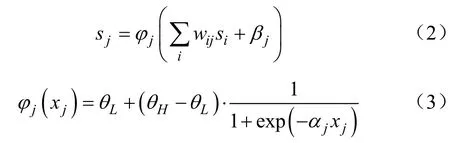
该函数为渐近线在θL和θH处的sigmoid函数。参数αj决定函数曲线的斜率，亦称之为噪声控制参数；阈值为常数σ和标准高斯分布Nj(0,1)组合成的一个随机噪声输入分量，非固定值，其概率分布为：

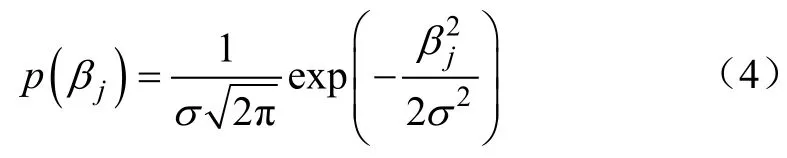
参考连续性Hopfield神经网络，可获得CRBM的能量函数[34]：

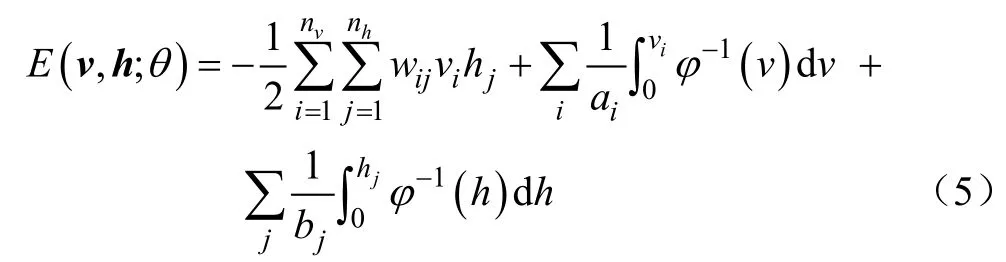
式中θ为模型参数，包括模型权值 wij、可视层噪声控制参数αj以及隐含层噪声控制参数bj。

CRBM模型参数是依据能量函数通过最大似然准则进行无监督学习得到的，通常采用最小化对比散度（minimizing contrastive divergence，MCD）进行wij、αi以及bj的迭代更新：

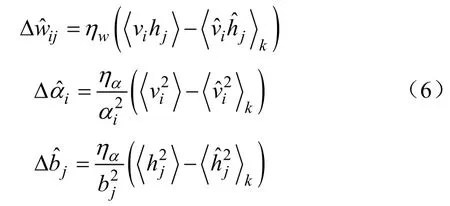
2.3 CDBN

CDBN的结构与DBN的类似，是一个多隐含层的混合概率图模型，但每层采用CRBM堆叠，能够处理输入输出都是连续型的数据。较之连续自编码网络，CDBN多了反向微调，能够充分利用有标签数据对模型进行训练。

根据概率图论模型（probabilistic graphical models,PGM）[35-37]，可得CDBN模型的联合分布如图2所示。

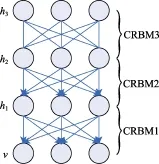
图2 连续深度置信网络CDBN概率图模型Fig.2 Probabilistic graph model of continuous deep belief networks CDBN

若令h0=X，则上式可写成：

式中X为可视层的状态向量。hk为第k层隐含层的状态向量。由D-separation可知，在自上而下生成过程中，各层中任意一个神经单元都是条件独立于该层中其他神经单元。因此，与DBN类似，CDBN在训练时可视作多个CRBM的堆叠训练，训练步骤如下：1）逐层预训练：采用无监督学习方法即式（6），自下而上训练每相邻两层神经元作为一个CRBM，最后将训练好的多个CRBM堆叠有序展开；2）反向微调：以有标签数据作为训练数据，采用BP进行反向微调，与DBN不同的是，CDBN反向微调时除了对连接权值W微调外，还需要对各个神经元的噪声控制参数α进行微调，此外，CDBN中神经元的阈值β为高斯分布的随机噪声输入分量，无需反向微调。

训练好后的CDBN可通过逐层非线性变换，实现从高维原始输入数据到低维特征空间的自动抽象表达。因此，CDBN实质上也是一种流形学习算法，完全符合流形学习定义，且可解决 “out of sample”问题。

2.4 基于CDBN+ELM的皮带秤在线跑偏检测

首先用样本数据训练一个3层CDBN对原始传感器数据进行跑偏特征提取，再在CDBN顶层向上增加一层回归层对提取后的特征进行跑偏量预测，回归层可以是BP、多元线性回归、SVM、ELM等。

模型反向微调时，为提高微调效率，最后一层采用多元线性回归；同时由于样本有限且为保证最终跑偏量预测的泛化性能，微调后最后一层置换成了正则化ELM，即优化包含经验风险项和正则化项的损失函数[36-37]：

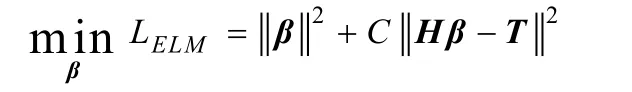
基于CDBN的在线跑偏检测模型示意图及其构建步骤如图3。

图3 基于CDBN跑偏检测模型示意图及其构建步骤图Fig.3 Schematic diagram and construction steps of online detection model of deviation based on CDBN

对比图1、3，二者最终获得的都是一个深层神经网络，各自都是在前三层实现了跑偏特征的表达，在最后一层采用ELM进行跑偏量预测。不同的是，前者是在LTSA处理原始数据后间接获得，后者是采用原始数据直接训练获得。

3 跑偏检测试验验证与分析

以南京三埃工控股份有限公司QPS皮带秤全性能试验中心的3#和4#阵列式皮带秤（array belt weigher，ABW）为对象进行跑偏在线检测试验（图 4），3#和 4 #阵列式皮带秤具体参数如表1。标准跑偏量样本数据采用文献[7,38]中方法获得，跑偏检测数据与现有传感器统一采用Modbus/RS485总线与测试笔记本通信，故现场采样同步，采样频率均为10 Hz。训练样本数据共15 797组，为3# ABW在空载，300、600 t/h（最大流量约为800 t/h）流量下的试验数据构成，其中有标签数据（有跑偏量数据）共6 718组。每组数据都是15维，各维度分别是输送带宽度、托辊间距、托辊槽角、8个称质量单元数据、现场温度、现场湿度、皮带秤实时平均流量、输送带实时运行速度。在线测试数据维度与样本数据相同，皆为有标签数据，对应实时标准跑偏量采用同样方法获得。试验中，皮带跑偏为人为制造。通常认为跑偏量超过输送带宽度±10%为输送带跑偏，但为保证安全，试验时跑偏量人为控制在±20%以内。输送带跑偏时跑偏量控制在12%～20%，未跑偏时控制在0～5%，以明显区别跑偏和未跑偏。

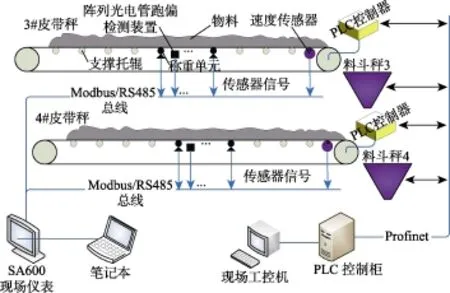
图4 QPS皮带秤全性能试验中心原理示意图Fig.4 Schematic diagram of full performance test center of QPS belt scale

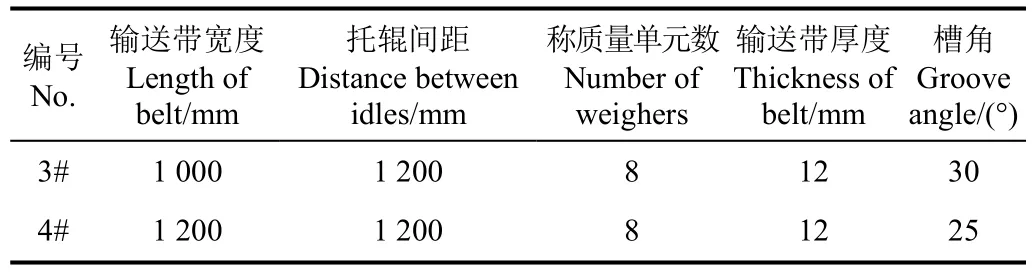
表1 3号和4号皮带秤参数Table 1 Parameters of 3# and 4 #array belt weigher

测试试验分别在3#ABW的空载、300、600 t/h以及4#ABW的空载，200、500、800 t/h（最大流量1 000 t/h）下进行。测试试验分为跑偏特征提取和在线跑偏量预测两部分：首先分别采用1.2节和2.4节两种降维方法进行跑偏特征提取试验；其次在跑偏特征模型的基础上，进行在线跑偏量预测试验。

3.1 预处理过程

预处理的目的是在模型训练或测试之前对模型输入数据进行规范化，统一量纲以便后续模型训练和测试、提高收敛速度，本节对输入数据的所有维度独立采用min-max标准化，手动设置各维度的最大值和最小值，统一归一化到[0,1]区间。

3.2 基于LTSA+GRNN的跑偏特征提取试验

先对原始数据进行预处理，然后分别采用PCA、Isomap、LLE、LTSA几种流形算法对9 079组无标签样本数据进行降维，目标维数d均设置为3，得到三维无量纲跑偏特征数据。以3#阵列式皮带秤300 t/h的样本数据为例，各算法降维效果如图5所示。

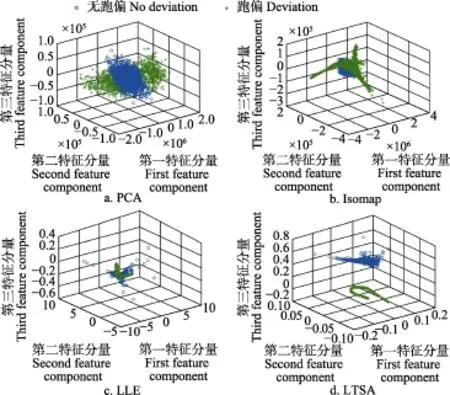
图5 各降维方法的降维效果图Fig.5 Dimension reduction results of various methods

图5显示，PCA、Isomap、LLE降维后的三维跑偏特征和未跑偏特征均存在很多重叠，同类数据降维后的聚类程度不高，会给进一步的跑偏预测造成困难，其中PCA重叠最为严重，失真较为严重。而采用LTSA降维后的跑偏特征和未跑偏特征能完全被区别分离，具有较好的特征提取效果，故而本文采用GRNN对LTSA降维后的非线性映射进行构建。为了降低GRNN模型的复杂度、提高GRNN预测速度，随机抽取样本数据中部分数据进行建模，并采用建立后的GRNN对所有原始样本（包括有标签和无标签数据）进行降维，其效果如图6。

图6 结合LTSA+GRNN降维效果图Fig.6 Dimension reduction result combined with LTSA+GRNN

从图6中可以看出，GRNN对LTSA降维后产生的非线性映射具有很好的逼近能力，能够很好地从高维数据空间中恢复跑偏低维流形，同时对于同一流量的跑偏和未跑偏特征向量具有很好聚类效果。但各个流量之间依旧有重叠部分。

3.3 基于CDBN的跑偏特征提取试验

依照2.4节，首先建立输入数据维度都为15、输出维度都为3、深度分别为2、3、4的CDBN模型，并采用同样的无标签训练数据进行预训练；其次，增加一LR层为线性输出层，并设置dropout为0.5，采用有标签跑偏数据进行反向微调；最后使用得到3种深度的CDBN模型份对原始数据进行降维试验，降维效果如图7。

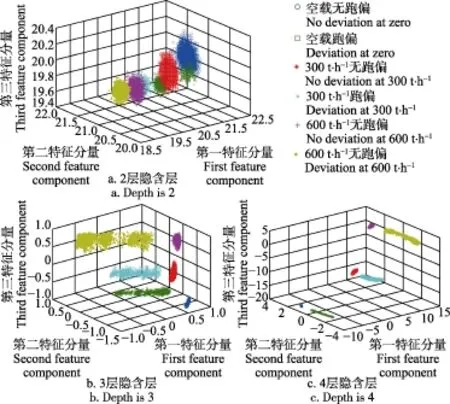
图7 不同深度的CDBN降维效果图Fig.7 Dimension reduction results using CDBN of different depths

从图7中比较可以确定，3层隐含层的CDBN提取出的跑偏特征能够满足需求。相较于LTSA，深度为3的CDBN不仅能对于同一流量的跑偏和未跑偏特征向量具有很好聚类效果，而且对不同流量依旧有很好聚类效果。此外，从图中可以看出皮带秤流量越大时，跑偏和未跑偏特征的欧式空间距离越大，说明皮带秤一旦发生跑偏，则流量越大，产生的跑偏量就越大，反之亦然。

3.4 在线跑偏检测试验及分析

本节试验中，先分别采用上述建立好的GRNN和CDBN对有标签样本数据针进行跑偏特征提取；再对其特征分别采用ELM建立各自对应的跑偏量预测模型；最后以3#和4#皮带秤在线实时数据分别对本文提出的模型进行验证，并与其他模型的试验结果进行比较分析，其中CDBN+LR、CDBN+SVM和CDBN+ELM的深度皆为3。所有模型输出数据皆携有原始传感器数据的采样时间，处理试验结果时，将各模型预测的跑偏量分别与对应相同采样时间的标准跑偏量（即阵列式光电管跑偏检测装置实时同步检测到的跑偏量）进行比较，得到具体试验结果如表2、3。

表2、3显示，LTSA+GRNN+ELM、CDBN+LR和CDBN+ELM三个模型的预测精度远高于ELM的82.9%和PCA+SVM的78.67%，均达到了90%以上；SVM和ELM的预测能力相当，但ELM的训练、预测速度要远快于SVM[39]。上述表明：LTSA+GRNN和CDBN都有效降低原始数据的冗余且保留了足够多的跑偏特征，明显提高了跑偏在线检测的精确度、减小了模型复杂度；ELM更适合于在线皮带跑偏检测。两表的对比可以得到：结合dropout技术和正则化ELM明显提高了跑偏检测模型的泛化性。进一步，结合皮带秤的不同工作场合，可以得到：LTSA+GRNN+ELM模型平均跑偏预测精度为93.33%，相对较高，训练时间18.91 s，也相对较短，但其预测速度并不很快，平均每组预测时间38.29 ms，故很适用于皮带秤称重标定较为频繁（每次标定完后，称重传感器相关参数会被修改，故跑偏预测模型需要重新训练）、实时性要求相对不高场合，如皮带秤实验室、衡器检定等；CDBN+ELM模型训练时间最长，达139.96 s，但其预测精度最高，达98.61%、平均每组测试时间也相对较短，只有1.47 ms，故非常适用于标定相对不频繁、实时性和预测精度要求较高的场合，如码头、粮库等衡器工作现场。

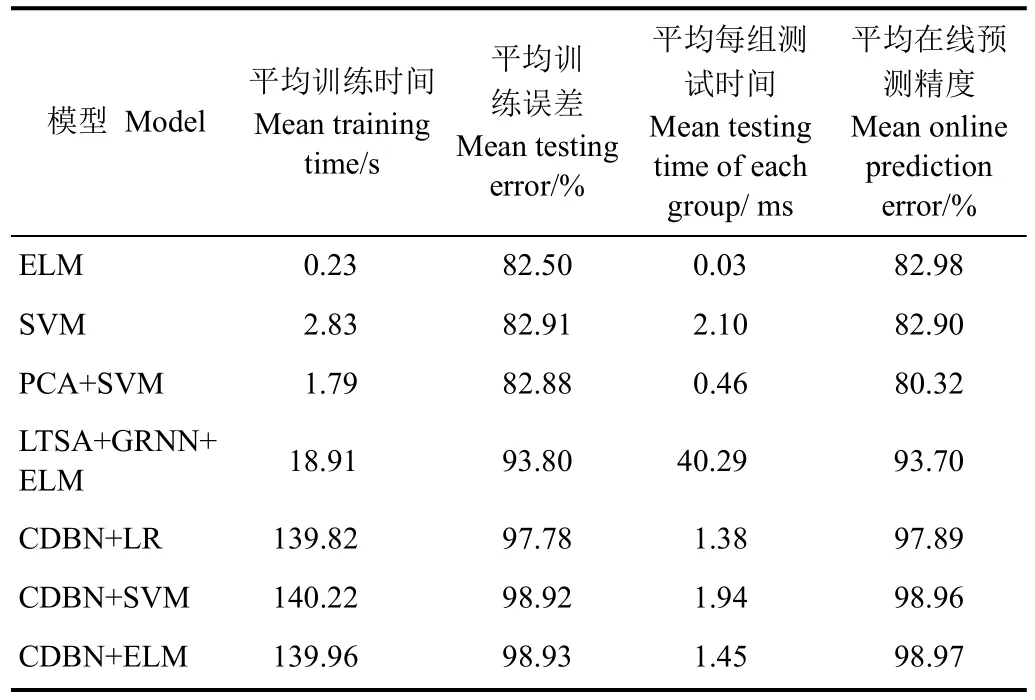
表2 各模型在3#皮带秤不同流量下的跑偏检测试验结果Table 2 Test results of various deviation detection models on 3# belt weigher at different flow rates

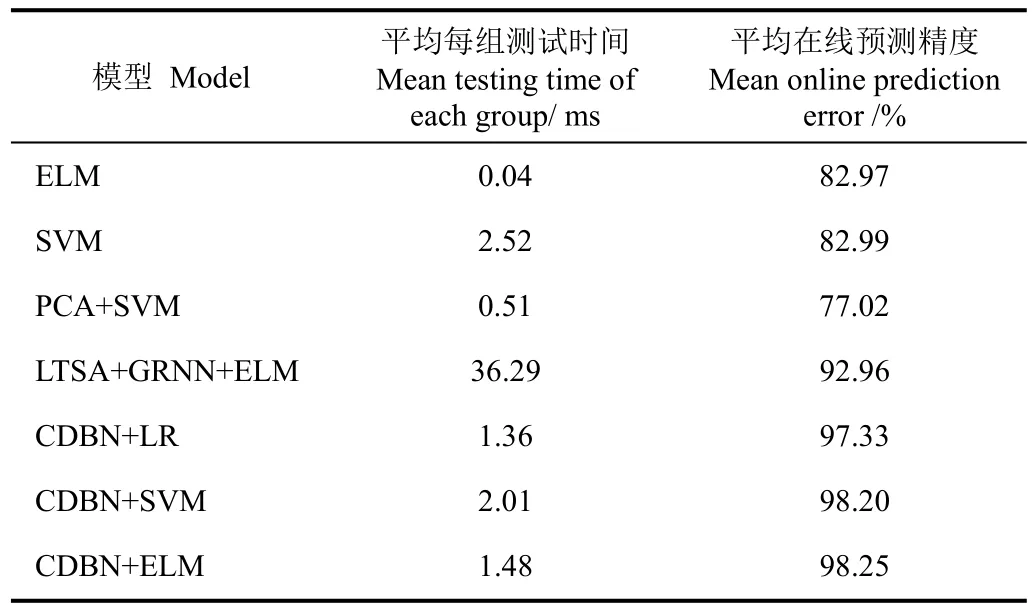
表3 各模型在4#皮带秤不同流量下的跑偏检测试验结果Table 3 Test results of various deviation detection models on 4# belt weigher at different flow rates

4 结 论

1）为实现皮带跑偏在线检测，针对原始传感器数据高维度、非线性相关，引入流形学习，并针对“out of sample”问题采用广义回归神经网络（generalized regression neural networks,GRNN）构建显性非线性映射，然后通过试验对比多种流形学习算法，得出局部切空间排列（local tangent space alignment,LTSA）LTSA+GRNN模型在皮带秤各个流量阶段皆具有较好的跑偏特征提取效果；

2）引入连续玻尔兹曼机，结合 d ropout技术，提出一种连续深度置信网络，并将其应用于皮带跑偏特征提取，试验表明，基于连续深度置信网络（continuous deep belief networks,CDBN）的跑偏特征提取模型同样具有较好的降维效果；

3）采用SVM、极限学习机（extreme learning machine,ELM）等回归分析方法、以在线提取到的跑偏特征为输入构建在线皮带跑偏量预测模型，并分别在参数不同的皮带秤上进行试验，试验结果表明：LTSA+GRNN+ELM和CDBN+ELM模型在不同皮带秤的不同流量下皆具有良好的皮带跑偏预测精度和泛化性能，精度均超过了90%，后者更是达到了98.61%；二者皆具有较好实时性，后者平均每组测试时间只有1.47 ms，但前者训练时间相对较短；二者皆可取代传统硬件跑偏检测设备，避免额外检测设备的制造、安装维修成本，符合生产商和客户的需求。此外，该研究为进一步的皮带秤在线精度补偿和故障预测提供了必要依据。

[1] 僧东恒. 皮带机跑偏的分析和治理措施[J]. 水利电力机械，2007，29(8)：92－94. Seng Dongheng. Analysis of the belt conveyor running deviation and its improvement[J]. Water Conservancy &Electric Power Machinery,2007,29(8):92－94.(in Chinese with English abstract)

[2] 董甲东，谷立臣. 带式输送机纠偏装置液压伺服系统仿真设计[J]. 起重运输机械，2010(11)：17－20. Dong Jiadong,Gu Lichen. Simulation design of the hydraulic servo system of the belt conveyor correcting device[J]. Hoisting and Conveying Machinery,2010(11):17－20.(in Chinese with English abstract)

[3] 刘文亮，张晓伟，董秋艳. 连续皮带机胶带跑偏原因与力学分析[J]. 水利水电技术，2006，37(3)：26－27. Liu Wenliang,Zhang Xiaowei,Dong Qiuyan. Cause and dynamic analysis of deviation of belt for belt conveyer[J]. Water Resources and Hydropower Engineering,2006,37(3):26－27.(in Chinese with English abstract)

[4] 张佳伟，楼佩煌. 输送皮带跑偏自动化检测及液压矫正技术[J]. 机械工程师，2008(10)：26－28. Zhang Jiawei,Lou Peihuang. Automatic detection and hydraulic correction technology of belt deviation[J]. Mechanical Engineer,2008(10):26－28.(in Chinese with English abstract)

[5] 段洁，孙向阳，蔡敬海，等. PSD在激光位移检测系统中的应用研究[J]. 红外与激光工程，2007(S1)：281－284. Duan Jie,Sun Xiangyang,Cai Jinghai,et al. Applications research to PSD in the laser displacement detecting system[J]. Infrared and Laser Engineering,2007(S1):281－284.(in Chinese with English abstract)

[6] 李妍，朱亮，袁延强，等. 基于阵列式光电三极管的皮带跑偏检测技术研究与系统设计[J]. 机床与液压，2014(3)：127－131.Li Yan,Zhu Liang,Yuan Yanqiang,et al. Research and design of detection system for belt deviation based on array phototransistors[J]. Machine Tool and Hydraulics,2014(3):127－131.(in Chinese with English abstract)

[7] 朱亮，李东波，李妍，等. 基于FPGA＋MCU的皮带跑偏检测系统研究与设计[J]. 机床与液压，2014(7)：86－89，95. Zhu Liang,Li Dongbo,Li Yan,et al. Research and design of detection system for belt deviation based on FPGA+MCU[J]. Machine Tool and Hydraulics,2014(7):86－89,95.(in Chinese with English abstract)

[8] 庞苏娟. 基于DSP的电子皮带秤设计与实现[D]. 西安：陕西科技大学,控制科学与工程，2012. Pang Sujuan. Design and Implementation of Electronic Belt Scale Based On DSP[D]. Xian:Shaanxi University of Science and Technology,Control Science and Engineering,2012.(in Chinese with English abstract)

[9] 黄添强. 数据挖掘算法与应用[M]. 厦门:厦门大学出版社，2011.

[10] 王珏，周志华，周傲英. 机器学习及其应用[M]. 北京：清华大学出版社，2006.

[11] 高亚文，汤海青，欧昌荣，等. 基于前表面荧光光谱鉴别新鲜与冻融大黄鱼[J]. 农业工程学报，2016,32(16)：279－285. Gao Yawen,Tang Haiqing,Ou Changrong,et al. Differentiation between fresh and frozen-thawed large yellow croaker based on front-face fluorescence spectroscopy technique[J]. Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE),2016,32(16):279－285.(in Chinese with English abstract)

[12] 岳学军，全东平，洪添胜，等. 不同生长期柑橘叶片磷含量的高光谱预测模型[J]. 农业工程学报，2015,31(8)：207－213. Yue Xuejun,Quan Dongping,Hong Tiansheng,et al. Prediction model of phosphorus content for citrus leaves during different growth periods based on hyperspectrum[J]. Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE),2015,31(8):207－213.(in Chinese with English abstract)

[13] Timonen J,Stirland M,Pilling D J,et al. An information geometry of statistical manifold learning[J]. Physical Review Letters,2015,56(21):2233－2236.

[14] Wang Qian,Wang Weiguo,Nian Rui,et al. Manifold learning in local tangent space via extreme learning machine[J]. Neurocomputing,2016,174:18－30.

[15] 詹宇斌，殷建平，刘新旺. 局部切空间对齐算法的核主成分分析解释[J]. 计算机工程与科学，2010(6)：158－161. Zhan Yubin,Yin Jianping,Liu Xinwang. A kernel PCA view of the local tangent space alignment algorithm[J]. Computer Engineering and Science,2010(6):158－161.(in Chinese with English abstract)

[16] Zhang Zhenyue,Zha Hongyuan. Principal manifolds and nonlinear dimension reduction via local tangent space alignment[J]. Siam Journal of Scientific Computing,2002,26:313－338.

[17] Mendoza Quispe Arturo,Petitjean Caroline,Heutte Laurent. Extreme learning machine for out-of-sample extension in Laplacian eigenmaps[J]. Pattern Recognition Letters,2016,74(C):68－73.

[18] Li Bo,Li Jun,Zhang XiaoPing. Nonparametric discriminant multi-manifold learning for dimensionality reduction[J]. Neurocomputing,2015,152:121－126.

[19] Orsenigo Carlotta,Vercellis Carlo. Kernel ridge regression for out-of-sample mapping in supervised manifold learning[J]. Expert Systems with Applications,2012,39(9):7757－7762.

[20] Lin Y Y,Liu T L,Fuh C S. Multiple kernel learning for dimensionality reduction[J]. IEEE Transactions on Software Engineering,2010,33(6):1147－1160.

[21] Li Xuelong,Lin S,Yan Shuicheng,et al. Discriminant locally linear embedding with high-order tensor data[J]. IEEE Transactions on Systems Man &Cybernetics Part B,2008,38(2):342－352.

[22] 刘昶，周激流，郎方年，等. 基于加权判别局部多线性嵌入的人脸识别[J]. 仪器仪表学报，2011(10)：2248－2255. Liu Chang,Zhou Jiliu,Lang Fangnian,et al. Weighted discriminative locally multi-linear embedding algorithm for face recognition[J]. Chinese Journal of Scientific Instrument,2011(10):2248－2255.(in Chinese with English abstract)

[23] Kim Kyoungok,Lee Daewon. Inductive manifold learning using structured support vector machine[J]. Pattern Recognition,2014,47(1):470－479.

[24] Liu Bing,Xia Shixiong,Meng Fanrong,et al. Extreme spectral regression for efficient regularized subspace learning[J]. Neurocomputing,2015,149:171－179.

[25] Liu Yong,Wang Qicong,Jiang Yi,et al. Supervised locality discriminant manifold learning for head pose estimation[J]. Knowledge-Based Systems,2014,66:126－135.

[26] Bengio Yoshua. Learning deep architectures for AI[J]. Found. Trends Mach Learn,2009,2(1):1－127.

[27] Hinton G E,Osindero S,Teh Y W. A fast learning algorithm for deep belief nets[J]. Neural Comput,2006,18(7):1527－1554.

[28] Mihoub Alaeddine,Bailly Gérard,Wolf Christian,et al. Graphical models for social behavior modeling in face-to face interaction[J]. Pattern Recognition Letters,2016,74:82－89.

[29] Hinton G E. A practical guide to training restricted boltzmann machines[J]. Momentum,2010,9(1):599-619.

[30] Tran Van Tung,AlThobiani Faisal,Ball Andrew. An approach to fault diagnosis of reciprocating compressor valves using Teager-Kaiser energy operator and deep belief networks[J]. Expert Systems with Applications,2014,41(9):4113－4122.

[31] 胡昭华，樊鑫，梁德群等. 基于双向非线性学习的轨迹跟踪和识别[J]. 计算机学报，2007(8)：1389－1397. Hu Zhaohua,Fan Xin,Liang Dequn,et al. Trajectory tracking and recognition using bi-directional nonlinear Learning[J]. Chinese Journal of Computer,2007(8):1389－1397.(in Chinese with English abstract)

[32] 胡昭华，宋耀良. 基于 A utoencoder网络的数据降维和重构[J]. 电子与信息学报，2009(5)：1189－1192. Hu Zhaohua,Song Yaoliang. Dimensionality reduction and reconstruction of data based on autoencoder network[J]. Journal of Electronics and Information Technology,2009(5):1189－1192.(in Chinese with English abstract)

[33] Hinton G E,Srivastava N,Krizhevsky A,et al. Improving neural networks by preventing co-adaptation of feature detectors[J]. Computer Science,2012,3(4):212-223.

[34] Hopfield J. J. Neurons with graded response have collective computational properties like those of two-state neurons.[J]. Proceedings of the National Academy of Sciences,1984,81(10):3088－3092.

[35] Bishop Christopher M. Pattern Recognition and Machine Learning[M]. Springer,2006.

[36] Huang GuangBin. An insight into extreme learning machines:random neurons,Random Features and Kernels[J]. Cognitive Computation,2014,6(3):376－390.

[37] 邹伟东，张百海，姚分喜等. 基于改进型极限学习机的日光温室温湿度预测与验证[J]. 农业工程学报，2015，31(24)：194－200. Zou Weidong,Zhang Baihai,Yao Fenxi,et al. Verification and forecasting of temperature and humidity in solar greenhouse based on improved extreme learning machine algorithm[J]. Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE),2015,31(24):194－200.(in Chinese with English abstract)

[38] 朱亮，李东波，李妍，等. 基于RS485/Modbus皮带跑偏检测传感网络的研究与实现[J]. 中国农机化学报，2014(4):217－220. Zhu Liang,Li Dongbo,Li Yan,et al. Design and implementation of belt deviation detection sensor network based on RS485/Modbus[J]. Journal of Chinese Agricultural Mechanization,2014(4):217－220.(in Chinese with English abstract)

[39] 宦娟，刘星桥. 基于K-means聚类和ELM神经网络的养殖水质溶解氧预测[J]. 农业工程学报，2016,32(17)：174－181. Huan Juan,Liu Xingqiao. Dissolved oxygen prediction in water based on K-means clustering and ELM neural network for aquaculture[J]. Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE),2016,32(17):174－181.(in Chinese with English abstract)

Detection of belt deviation of belt weigher using data mining

Zhu Liang1,Li Dongbo2,Wu Chongyou1,Wu Shaofeng2,Yuan Yanqiang3
(1. Nanjing Institute of Agricultural Mechanization,Ministry of Agriculture,Nanjing 210094,China;2. School of Mechanical Engineering,Nanjing University of Science &Technology,Nanjing 210094,China;3. Nanjing Sanai Industrial Co.,Ltd,Nanjing 211100,China)

At present,belt weigher has been widely used in various transportation and trade occasions of industry and agriculture. Belt deviation is one of the most important indicators of accuracy of belt weigher,and it is also one of the most common faults. In this paper,aiming at the problem of belt deviation,we obtained the real-time online detection of deviation by the data mining based on the existing original sensor data of belt weigher,instead of traditional hardware testing equipment in which CCD,PSD and array phototransistor are usually used as the specialized sensor for detecting deviation. At first,in order to reduce the dimension of existing original data and the complexity of the subsequent detection mode of belt deviation,the online features extraction models of belt deviation based on LTSA(Local Tangent Space Alignment) + GRNN(Generalized Regression Neural Networks),and CDBN(Continuous Deep Belief Networks) were proposed respectively,through introducing manifold learning and deep learning. GRNN was applied to construct the explicit nonlinear mapping from the original data of high dimension to the features of belt deviation extracted by LTSA. CDBN was proposed by introducing CRBM(Continuous Restricted Boltzmann Machine) and combining with the "dropout". Unlike LTSA,CDBN can be used to construct the explicit nonlinear mapping while extracting the deviation features from the original data,which needed more training time. Subsequently,the feature extraction experiments of belt deviation at different flow rates showed that the models based on LTSA+GRNN,and CDBN both had very good feature detection effect which meant that the two features extraction models could effectively reduce the redundancy of the original data while retaining enough features of belt deviation. And the experiments also revealed that,in case of belt deviation,the bigger the flow rate was,the greater the amount of belt deviation was,and vice versa. Further,SVM(Support Vector Machine),ELM(Extreme Learning Machine) and other regression analysis methods were used to build the online prediction models of belt deviation where the deviation features extracted by LTSA+GRNN and CDBN were taken as the input. Finally,the performances of two proposed online detection models of belt deviation based on LTSA+GRNN+ELM and CDBN+ELM respectively were verified through the experiments:the average prediction accuracy of deviation prediction model based on LTSA+GRNN+ELM was 93.33%,while its average prediction time of each group was 38.29 ms and its average training time was 18.91 s;the average prediction accuracy of deviation prediction model based on CDBN was as high as 98.61%,while its average prediction time of each group was as short as 1.47 ms and its average training time was 139.96 s. Besides,the experiments also showed that ELM was more suitable than SVM for the belt deviation,because ELM had almost the same prediction accuracy as SVM while the training and prediction time of ELM was far less than that of SVM. Both the prediction and real-time of the two models mentioned above showed that the two models could be a new approach for online detection of belt deviation and replaced traditional hardware detection device. Moreover,this study provided the necessary basis for the further online precision compensation and fault prediction of belt weigher.

data mining;sensors;models;belt deviation;manifold learning;continuous deep belief networks;extreme learning machine

10.11975/j.issn.1002-6819.2017.01.014

TH165;S237

A

1002-6819(2017)-01-0102-08

朱 亮，李东波，吴崇友，吴绍锋，袁延强. 基于数据挖掘的电子皮带秤皮带跑偏检测[J]. 农业工程学报，2017，33(1)：102－109.

10.11975/j.issn.1002-6819.2017.01.014 http://www.tcsae.org

Zhu Liang,Li Dongbo,Wu Chongyou,Wu Shaofeng,Yuan Yanqiang. Detection of belt deviation of belt weigher using data mining [J]. Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE),2017,33(1):102－109.(in Chinese with English abstract)doi：10.11975/j.issn.1002-6819.2017.01.014 http://www.tcsae.org

2016-05-18

2016-10-23

科技型中小企业技术创新基金（13C26213202062）

朱 亮，男，江苏扬州人，博士，主要从事智能检测与控制、人工智能与机器学习。南京 农业部南京农业机械化研究所，210094。Email：676205493@qq.com