战略投送视角下军事交通运输网络抗毁性仿真

陈博文，钟 敏

(军事交通学院 基础部，天津 300161)

● 战略投送 Strategic Projection

战略投送视角下军事交通运输网络抗毁性仿真

陈博文，钟 敏

(军事交通学院 基础部，天津 300161)

基于现代网络科学理论，针对军事交通运输网络特性，从战略投送任务视角分析军事交通运输网络的拓扑结构，建立具体的军事交通运输加权网络模型，提出偏α介数作为分析战略投送任务下军事交通运输网络抗毁性的特征量，对军事交通运输网络的抗毁性进行仿真模拟分析，并结合网络模型仿真结果，给出军事交通运输网络抗毁性对策与建议。

军事交通运输网络；战略投送；抗毁性；偏α介数

军事交通运输网络是国家可以用于军事运输的铁路、公路、水路、航空等运输网络组成的现代综合运输体系，涉及军队、地方政府和企事业单位等多个主体。战略投送是为达成一定的战略目的、综合运用各种运输力量向作战或危机地区投入兵力集团的行动[1]。在某种意义上，战略投送的成功与否已经成为决定现代战争胜负的重要因素之一。战略投送的重要性，使得军事交通运输网络中的关键部位或者薄弱环节成为敌方为破坏战略投送而进行有目的干扰、破坏的主要对象，在敌方高精度、强火力武器的打击下，军事交通运输网络中关键部位或者薄弱环节的损毁，将严重威胁战略投送任务的顺利完成，甚至可能影响到战争胜负。

研究网络抗毁性正是为了正确评价网络、发现网络的关键部位和薄弱环节，从而采取有效的优化措施，提高网络的抗毁性。现有文献[2—13]多从无权网络的角度研究网络的抗毁性，而加权网络，由于边与点所拥有的不同权值，使得其网络性质的描述与计算很复杂，因而少有针对加权网络的抗毁性研究。本文研究战略投送任务要求下军事交通运输加权网络的抗毁性。

1 战略投送视角下军事交通运输加权网络模型

在以往的研究中，关注重点是军事交通运输网络整体的性能。而对于具体的战略投送任务，更关心哪些具体的运输线路或者局部在遭受攻击后，会影响战略投送任务的完成。以华北某地到东北边境某地的战略投送任务为例，投送方式有铁、公、水、空等多种选择路径。由于各种投送方式的投送速度不同，路程的长短并不能代表投送的快慢，因此将网络中各边的权值确定为对应运输方式通过相应路段所用时间。还需要考虑运输装载准备时间，特别是必须考虑不同运输方式之间转换所消耗的时间。比如，由公路转为铁路投送时在很大程度上受限于装备的需求和平板车的调度，而转为海运则更受所调集的船只大小、种类、适于装卸的形式等的限制。经过调研与分析，本文根据各种运输方式之间转换的理想状态，估计各运输方式之间转换的时间。

想定的战略投送任务下，军事交通运输加权网络示意如图1所示。

图1 战略投送任务下军事交通运输加权网络示意

2 网络抗毁性相关特征量

考虑战略投送视角，在军事交通运输网络中指定具体的投送任务起始地(origination，O)和目的地(destination，D)，研究军事交通运输网络节点或边的毁损对节点O、D间投送任务完成的影响。在已有的无权网络研究中，发现介数优先的攻击策略对一般网络的破坏较大，因此将介数这一概念引入到加权网络，利用这一指标来描述战略投送视角下的军事交通运输网络的抗毁性。

2.1 有效路径

有效路径的定义方法很多，本文借鉴文献[14]的有效路径定义：若OD对之间的路径k为有效路径，需满足：

(1)k为简单无环路径。

2.2 关于特定OD对的偏α介数

对于战略投送任务来讲，主要关心的是一个具体的出发点O与目的地D之间的道路和设施情况，而不太关心这些道路与设施对于其他点对之间的影响。因此，用有效路径代替无权网络介数定义中的最短路径，并针对具体的点对OD提出如下偏介数定义。

式中：φOD为O和D之间的所有路径伸展系数为α的有效路径数；φOD(v)为O和D之间经过点v的路径伸展系数为α的有效路径数。

式中φOD(e)为O和D之间经过边e的路径伸展系数为α的有效路径数。

如此定义的点或者边关于OD对的偏α介数，是一个不超过1的非负数。由定义不难看出，在网络中指定一个OD对之后，其点(或边)关于该OD对的偏α介数越大，该点(或边)对OD对之间的交通影响越大。在实际应用中，还可以根据不同的有效路径是否允许有相同路段分为对点(或边)关于OD对可重复或不可重复的偏α介数。

3 网络抗毁性仿真分析

已有研究表明，各种随机攻击策略对网络的攻击效果并不明显，因而只考虑敌方的蓄意攻击。将敌方对网络的攻击策略分为两种：一种是对网络节点的攻击策略，另一种是对网络边的攻击策略。对于军事交通运输网络而言，攻击节点意味着打击交通运输网络中的机场、港口、城镇、交通枢纽、桥梁、营区等；而对边的攻击则意味着毁伤节点间的公路、铁路路段，或控制空中或海运航线的必经空域或海域，使之不能通行，失去效用。

3.1 网络抗毁性仿真思路

执行投送任务时，出发点O和目的地D是确定的，为最快到达目的地，会选择最便捷的运输方式和线路。当O、D间的原计划投送路线上一些交通线路或设施遭到毁损后，部队会适时地更改路线而绕过被毁损的节点或路段，继续选择最便捷的运输方式和路线执行投送任务。为此，选用最短行程时间作为比较一条路线是否便捷的指标。把不同路段或航程的里程转化为不同运输方式所需要的时间，然后再计算O、D节点间不同路径的最短行程时间，找出最佳的交通方式和路线，这里仍称之为最短路径。

第一步，计算得到节点O到节点D的初始最短路径长度(最短行程时间)L0；第二步，按一定策略对整个路网若干节点进行删除后(即一次攻击后)，再次寻找O、D节点间的最短路径，并计算最短路径长度Li，i∈Z为攻击次数；第三步，根据最短路径长度Li判断：如果Li=∞或者时间延误超出了预计延误上限，则停止；否则重复第二步。

假定敌方事先清楚我方军事交通运输网络的各种物理信息，也能够对我投送方向做出准确的预判，并据此采取适当的攻击策略进行蓄意攻击，以对我交通运输网络造成有效的毁损。如果攻击方有足够的及时信息获取能力，它可以在每次攻击后，对攻击效果进行及时准确的评估，然后对攻击后的网络重新计算各节点和边的参数并按所得新参数进行下一次攻击，称之为动态方式，否则攻击方不能及时准确地评估攻击效果，只能一次性地确定好各次攻击的目标，称之为静态方式。

为研究方便，做如下假定：①不对网络各节点和边设定防护等级系数，假定敌方的一次攻击即可摧毁其事先选定的一个节点或一条边；②不考虑敌方的弹药储备等约束条件限制，假定攻击一方有能力无限制地攻击下去，直到达到预设目的或者击毁网络所有的节点或边为止；③假定一个节点失效后，其关联边也随之失效，即在网络中删除与该节点相连的所有边；④不考虑攻击方对投送任务出发点和目的地的攻击，尽管它们是攻击的首要目标，但只要对这两点中的任何一点进行了成功的攻击，将会使其他的问题再无意义。

3.2 节点攻击策略下的抗毁性分析

3.2.1 节点偏α介数优先的静态蓄意攻击策略的影响

由于α取值较大时的α有效路径数量庞大，计算的时间成本太高，这里α分别取值0.05、0.10、0.15为代表。设定每次攻击删除一个偏α介数值最大的节点，在Matlab平台上进行攻击模拟。考察攻击对最短行程时间造成的影响，结果如图2所示。

(a) α=0．05

(b) α=0．10

(c) α=0．15图2 OD对偏α介数优先的去点攻击策略最短行程时间变化

由图2可以看出，对于α=0.05、0.10和0.15等3种情况，分别需要9、16和18次攻击即可达到全部毁损预定接受范围的有效路径，毁损节点的比例分别为1.98%、3.52%和3.96%。而且，相比较于按度值大小的攻击策略，关于OD对去点的偏α介数攻击策略的毁损要严重得多。

3.2.2 节点偏α介数优先的动态蓄意攻击策略的影响

为方便比较，把不同α值的关于OD对偏α介数放在一起来讨论，基于时间成本原因，α分别取值0.05、0.10、0.15为代表。设定每次攻击去掉一个当前网络中某种介数值最大的一个节点，在Matlab平台上进行介数优先的去除节点攻击模拟。由于攻击效果太强，只需极少的攻击次数即可达到对投送时间的延误目标，以至于没有办法用图来表示(结果见表1)。

表1 OD对偏α介数优先去点蓄意攻击的影响

由表1可以看出，该攻击策略的效果十分显著。对于不同的α值其攻击效果略有差异，但都只需2次攻击，即可造成投送最短行程时间超过预定的延误比例。此时尽管实际中两地的交通并没有中断，但按所给定的α，已经没有对应的有效路径。

3.3 边攻击策略下的抗毁性分析

3.3.1 边偏α介数优先的静态蓄意攻击策略的影响

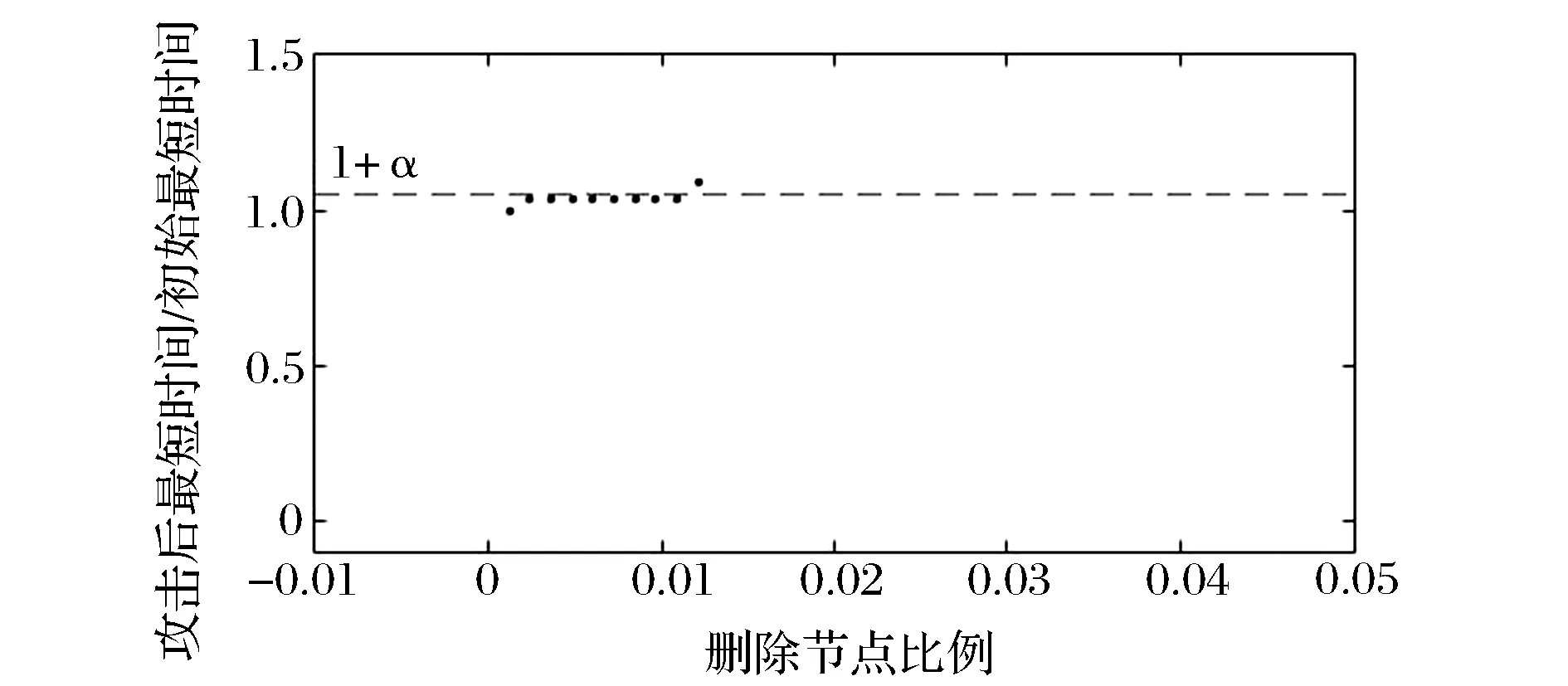
取α值为0.05、0.10、0.15，每次攻击去掉一个偏α介数值最大的边，攻击结果如图3所示。

不同的α值，攻击效果表现出一定的差异。对α=0.05，进行第8次攻击后，可使最短行程时间延误达到7.59%，此时边的去除比例是0.97%，已不存在所给α范围内的有效路径。对α=0.10，在第6次攻击后时间延误已经超过了9%。对α=0.15，第1次和第6次攻击造成了时间延误的跃升，在第20次攻击使时间延误达到了19.14%。 可以看到，这种攻击策略的毁损比较严重，甚至比对节点的蓄意攻击更严重。

(a) α=0．05

(b) α=0．10

(c) α=0．15图3 OD对偏α介数优先的去边攻击策略最短行程时间变化

3.3.2 边偏α介数优先的动态蓄意攻击策略的影响

同样假设敌方有足够的及时信息获取能力，在每轮攻击之后能够迅速、准确地评估出攻击效果，并据此确定下一轮的打击目标，这里取α的值为0.05、0.10、0.15，每次攻击删除当前网络偏α介数最大的边(结果见表2)。

由表2可以看出，该攻击策略的效果十分显著，即使对于较大的α值(α=0.15)，也仅需4次攻击即可达到预定目的。

表2 OD对偏α介数优先去边蓄意攻击的影响

4 仿真结果分析

(1)目前军事交通运输网络抗自然毁损能力强。通过随机去边和随机去节点的仿真可以看到，战略投送任务下，军事交通运输网络的抗自然毁损能力很强，要想使投送时间延误超过10%，大致需要去除10%左右的节点或边。这是因为，想定任务所涉及的交通网络区域位于我国中部和东北部，是包含我国政治经济中心(北京)在内的、拥有较好交通设施的局部网络。该地区交通网络发达、道路与节点密集、多种交通方式的道路纵横交织，不仅能较好地抵抗自然毁损，即使是面对恶意打击，其承受能力也是比较强的。

(2)偏α介数较大的边和节点都是最优毁伤策略的关键。关于OD对偏α介数高的节点和边，对投送任务来说都是非常关键的。对于军事交通运输网络，无论是去除节点还是边，在攻击方明确了我方投送方向的恶意攻击策略下，关于OD对的动态偏α介数优先的攻击策略毁损效果最强。

以节点为例，关于OD对节点的偏α介数的重要程度远高于度，从某种意义来说，度是有全局意义的指标，而偏α介数是与投送任务的OD对相关的指标。而且，关于OD对偏α介数大的网络节点，并不一定是度值大的节点。其现实意义在于，优先打击军事交通运输网络中的与投送任务相关的枢纽，会取得最优的毁伤效果。

想定的战略投送任务下，军事交通运输网络的节点往往是县以上城镇，一般都很大，且往往有环城公路，毁损困难，即纯粹易毁的交通枢纽节点不多。而边所代表的网络路段，长度有时达几百千米，公路、铁路路段大都有大型桥梁或隧道(我国公路约每6 km一座桥梁，每327 km一个隧道；铁路情况也类似)，只要摧毁其中的一座桥梁或隧道，就可以造成该路段的中断。对于敌方而言，攻击边比攻击节点容易。通过仿真，关于OD对的对边动态偏α介数优先的攻击策略毁损效果显著。一旦投送任务方向确定之后，要及时评估各节点与边的重要性，做好防护，准备好抢修抢建预案和力量。

(3)信息保密极其重要。尽管军事交通运输网络的抗毁性从全国的角度比较强，但从仿真结果看，在精确制导武器广泛应用的今天，在敌方动态关于OD对偏α介数优先策略的攻击下，其毁损其实是轻而易举的。交通网络设施一般是固定的、公开的，很难进行保密。因此，首先是对投送任务保密，使敌方不能够做出准确判断，不能针对投送任务的攻击等同于随机攻击，效果会大打折扣；其次是阻止敌方对攻击效果的及时信息收集，使其不能有针对性地准确制定下一步打击目标，这样的攻击等同于静态攻击，效果会打折扣。

5 结 语

本文仿真是对关于OD对可重复偏α介数优先攻击策略的静态和动态仿真，也进行了关于OD对无重复偏α介数优先攻击策略的静态和动态仿真，其毁损效果虽然不如关于OD对可重复偏α介数优先策略强，但也是很强的。由于两点间可重复路段的路径计算复杂，时间成本很高，而不重复的路径计算要简单得多，因此，在一般情况下，可以考虑用关于OD对无重复偏α介数来代替关于OD对可重复偏α介数。

[1] 刘继贤. 围绕战略投送能力的要求实行院校建设转型[J]. 军事交通学院学报, 2012，14(10):1-2.

[2] 胡兴雨，张学义，吴俊，等．网络结构抗毁性研究[J]. 计算机技术与发展，2010，20(1)：185-188．[3] 任连兴，单洪．基于效果评估的网络抗毁性研究[J]. 计算机与现代化，2010(1)：150-152．

[4] 李德毅,于全,江光杰.CI系统可靠性、抗毁性和抗干扰的统一评测[J].系统工程理论与实践,1997,17(3):23-27.

[5] ALBERT R,BARABASI A L.Error and attack tolerance of complex networks[J]. Nature,2000, 406：378-382.

[6] PETER H，BEOMKIM.Attack vulnerability of complex networks[J].Physical Review E, 2002, 272：130-131.

[7] XIE F，DAVID L．Measuring the structural vulnerability of road network[J]．Geographical Analysis，2007(39)：336-356．

[8] LUATIHEP P,SUMALEE A,HO H W.Large-scale road network vulnerability analysis： a sensitivity analysis based approach[J]．Transportation，2011(38)：799-817．

[9] IBRAHIM S，AMMAR R．An efficient heuristic for estimating transportation network vulnerability[J]．IEEE，2011:1092-1098．

[10] WAN Neng，ZHAN F B，CAI Zhongliang．A spatially weighted degree model for network vulnerability analysis[J]．Geo-spatial Information Science，2011，14(4)：274-281．

[11] ALAN T，MURRAY．An overview of network vulnerability modeling approach[J]．GeoJournal，2013(78)：209-221．

[12] FEDERICO Rupi，SILVIA Bernardi．The evaluation of road network vulnerability in mountain area: a case study[J]．Springer，2014．

[13] ODED C，ERIK J．Dynamic vulnerability analysis of public transport networks：mitigation effects of real-time information[J]．Springer，2014(14)：435-463．

[14] 李志纯，黄海军．随机交通分配中有效路径的确定方法[J]．交通运输系统工程与信息，2003，3(1)：28-32．

[15] 张建勇，李成江，黄汝存．联网高速公路有效路径伸展系数[J]．公路交通科技，2008，25(1)：116-119．

(编辑：张峰)

Invulnerability Simulation of Military Transportation Network from Perspective of Strategic Projection

CHEN Bowen, ZHONG Min

(General Courses Department, Military Transportation University, Tianjin 300161, China)

Considering the scientific theory of modern network and characteristic of military transportation network, the paper firstly analyzes the topological structure of military transportation network from the perspective of strategic projection and establishes weighted network model. Then, it takes α-betweenness as the characteristic and analyzes the invulnerability of military transportation network, and puts forward countermeasures and suggestions according to the simulation result of the network model.

military transportation network; strategic projection; invulnerability; α-betweenness

2016-08-21；

2016-09-08．

全军军事类研究生课题(2011TJ002-381，2012JY002-418)．

陈博文(1959—)，男，博士，教授，硕士研究生导师．

10．16807/j.cnki.12-1372/e.2017.01.002

E234

A

1674-2192(2017)01- 0005- 05