随机需求条件下生鲜农产品库存控制研究
2017-01-17王金妹陈小琼
王金妹 陈小琼
(福州大学经济与管理学院, 福建福州 350116)
随机需求条件下生鲜农产品库存控制研究
王金妹 陈小琼
(福州大学经济与管理学院, 福建福州 350116)
生鲜农产品具有需求随机、易发生变质、价格不稳定等特点,故生鲜农产品的库存控制问题不能简单运用经济订货批量模型来解决。在对生鲜农产品库存控制相关影响因素进行系统分析的基础上,考虑生鲜农产品的需求受到存货水平的影响,通过改进传统EOQ模型中价格不变的假设条件,建立随机需求条件下生鲜农产品库存控制模型,并对最优解的存在性和唯一性进行验证,最后结合算例进行灵敏度分析,并提出相应的库存控制策略。
生鲜农产品; 库存控制; 随机需求; 价格可变; 变质率
生鲜农产品作为人们的消费必需品,在日常生活消费中占据重要地位。但相关资料显示,我国蔬菜和水果摘取后的损耗率高达25%-30%,每年由此带来的经济损失高达1000亿元。[1]因此,如何采取有效的措施来控制和降低其损耗率显得尤为重要。这不仅需要提高生鲜农产品的生产质量,加强其在冷链物流系统的基础设施建设,而且需要做好生鲜农产品的库存控制。在生鲜农产品的库存控制方面,当前的多数经销商仍采用粗放式管理模式,通常是凭借自身的经验,根据以往销售量来制定进货量。然而,这种方式不但未能有效解决库存控制难题,反而使得库存控制变得更加复杂和严峻。由于生鲜农产品存在需求的随机性,经销商采取传统管理模式制定决策时容易放大需求信息,产生“牛鞭效应”,导致积压越来越多的库存,这是生鲜农产品产生巨大损耗的根本原因。可见,科学地认识生鲜农产品库存控制的影响因素,建立具有可操作性的库存控制模型,具有十分重要的现实意义。
生鲜农产品具有供给的时令性、价格的波动性、需求的全年性、易发生变质等特点,这些特点决定了生鲜农产品的库存问题不能简单运用经济订货批量模型来解决。Baker和Urban首先对存货影响需求率为幂指数函数的库存模型进行研究。[2]之后,Datta在Baker和Urban的研究基础上,进行了改进,指出当存货水平下降到一定程度(存货临界点)时,需求率会保持常数。[3]Fujiwara最早对生鲜农产品库存问题进行研究,将成本惩罚函数引入到了经典的易变质产品的库存模型中。[4]随后Padmanabhana 和Prem建立了考虑存货影响销售率的库存控制模型。[5]徐贤浩和李锐娟提出无形变质的概念,考虑不允许缺货情况,并假设需求率受到存货水平影响,无形变质率与需求率负相关,建立了短生命周期物品的库存模型。[6]但斌和陈军研究了确定性需求的生鲜农产品库存订货模型,构建了新鲜度衰减函数,并在此基础上讨论了以超市为主导的两级供应链协调策略。[7]肖勇波等在考虑生鲜农产品损耗率方面,主要分析了运输过程中新鲜度流失带来的损失风险和在零售市场上的销售风险,对供应链协调机制进行了研究。[8]凌六一等在农超对接的大环境下,考虑农产品产出和需求均带有随机性的情况,研究供应链协调机制问题,并重点分析了产出和需求不确定性对供应链成员最优决策的影响。[9]邓琪将易变质库存模型运用到生鲜农产品最优订货量的研究中,确定了同时考虑变质率和时间因素的最优订货周期和最优订货量。[10]王磊研究了生鲜农产品保鲜影响消费者效用下零售商的订货和订价策略。[11]Manish 和Sanjay对生鲜农产品供应链方面的相关文献进行梳理,指出当前关于生鲜农产品供应链的研究缺乏有效的需求预测,存在供需不匹配等问题,缺乏贴近实际特征的系统研究。[12]Fan Tijun等提出可以借助RFID技术对实时信息的搜集处理和传递能力,测定生鲜农产品的库存损耗率,从而制定相应的应对策略。[13]王丽娟和侯云先对Weibull分布的生鲜农产品库存控制问题进行了研究。[14]李琳和范体军针对生鲜农产品在价值损耗和消费者需求等方面的特点,建立适合不同模式的定价决策模型。[15]邱洪全运用系统动力学的方法对一个动态、多级的生鲜农产品供应链库存问题进行建模分析,研究表明,随着信息共享程度的提高,库存水平下降趋势愈发明显。[16]以上研究成果为生鲜农产品库存控制研究指明了方向。但现有文献对生鲜农产品库存控制问题的研究大多是在经济订货批量模型的基础上稍加改进而得到的,对于生鲜农产品库存的相关影响因素没有进行深入分析,特别是忽略了存货水平对于需求的影响,缺乏对需求、价格、变质三者关系的综合分析。
因此,本文基于随机需求的视角,从生鲜农产品的具体特征出发,对存货影响销售率的生鲜农产品库存控制模型进行深入分析,以期为生鲜农产品的经营活动提供一些理论依据和现实指导,从而实现优化生鲜农产品运营模式和提高经济效益的目的。
一、问题描述及模型假设
(一)问题描述
市场研究发现,消费者对某个产品的需求时常受到该产品存储数量的影响,当货架上摆放的产品越多,就越容易吸引更多的顾客并引发需求,这种现象被称为“存货影响需求率”——即需求率与库存水平呈正相关关系。对于生鲜农产品而言,其需求率也符合这一规律。生鲜农产品的生命周期很短,在销售过程中会发生物理变质,导致价值降低甚至为零。当库存充足,消费者有足够的选择余地,可以挑选他们认为足够新鲜的产品,需求增加;当库存较少,消费者选择余地不足,剩余产品是被挑剩下的,品质不够好,从而减少需求。
在存货影响需求率的研究中,一种假设需求率是订货批量的函数,一种假设需求率是实时库存水平的函数。[17][18]这些研究往往假设需求率为常数,但现实中需求率可能呈现为时间的线性函数、指数函数等。本文在Fujiwara O. U. L.研究[19]基础上,结合问题的实际特征,考虑缺货情况,并假设缺货引发缺货成本,建立了随机需求条件下生鲜农产品库存控制模型。为简化问题,本文考虑一个经销商销售一种生鲜农产品的情况,且假定其最初有一定量的库存满足消费者需求,直至库存为零。
(二)模型假设
(1)订货提前期为零,即瞬时补充;
(2)当库存量在存货临界点之上,需求率是存货的指数函数,当库存量小于等于存货临界点,需求率为常数,即当0≤S(t)
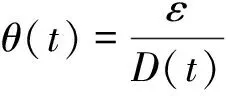
(4)允许缺货,令库存系统的缺货水平为r,则在整个订货周期内服务水平为(1-r);
(5)销售价格是外部需求的线性函数,即P=P′-λD(t)。
(三)符号定义
S(t):t时刻库存水平;
H:存货水平临界点;
Q:初始采购批量;
M:单位产品购买成本(即单位产品变质成本);
C:一次订购的成本;
h:单位产品单位时间内的持有成本;
R:单位产品的缺货成本;
TC:总成本;
DC:变质成本;
HC:持有成本;
SC:缺货成本;
AC:单位时间平均成本;
θ(t):t时刻变质率;
T:订货周期;
t0:存货水平下降到临界点的时间;
t1:存货朔评降为零的时间;
r:缺货水平,则t″=(1-r)T ;
P:单位产品销售价格;
P′:理论定价;
TR:销售收入;
W:总利润;
AU:平均利润。
二、模型的建立与求解
假设当存货量降到临界水平时,需求率将不再变化,所以生鲜农产品的库存控制模型的建立也可分为两种情况分别进行分析,即采购量大于存货水平临界点(Q>H)时的情况和采购量小于存货水平临界点(Q≤H)时的情况。
(一)数学模型
1. 当Q>H时的库存控制模型
库存状态如下:
(1)
根据边界条件,得到I(t′)=H,I(t″)=0,求解公式(1)可得
(2)
将t=0代入公式(2),可以得到一次订货批量
(3)
已知S(t″)=0,代入公式(2),得到
(4)
在该生鲜农产品库存控制系统中,库存控制总成本包括订货成本、库存持有成本、变质成本以及缺货成本,其中各项成本表示如下。
库存持有成本:
(5)
变质成本:
(6)
缺货成本:
(7)
因此,库存控制总成本为:
(8)
将假设条件t″=(1-r)T代入上式,得:
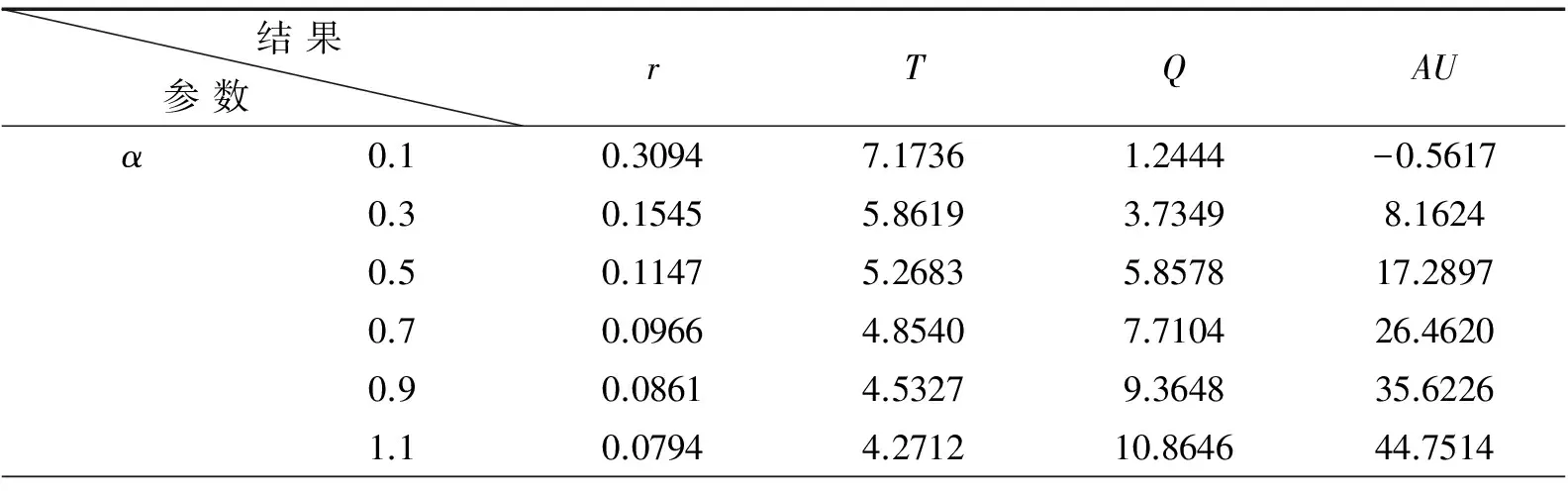
(9)
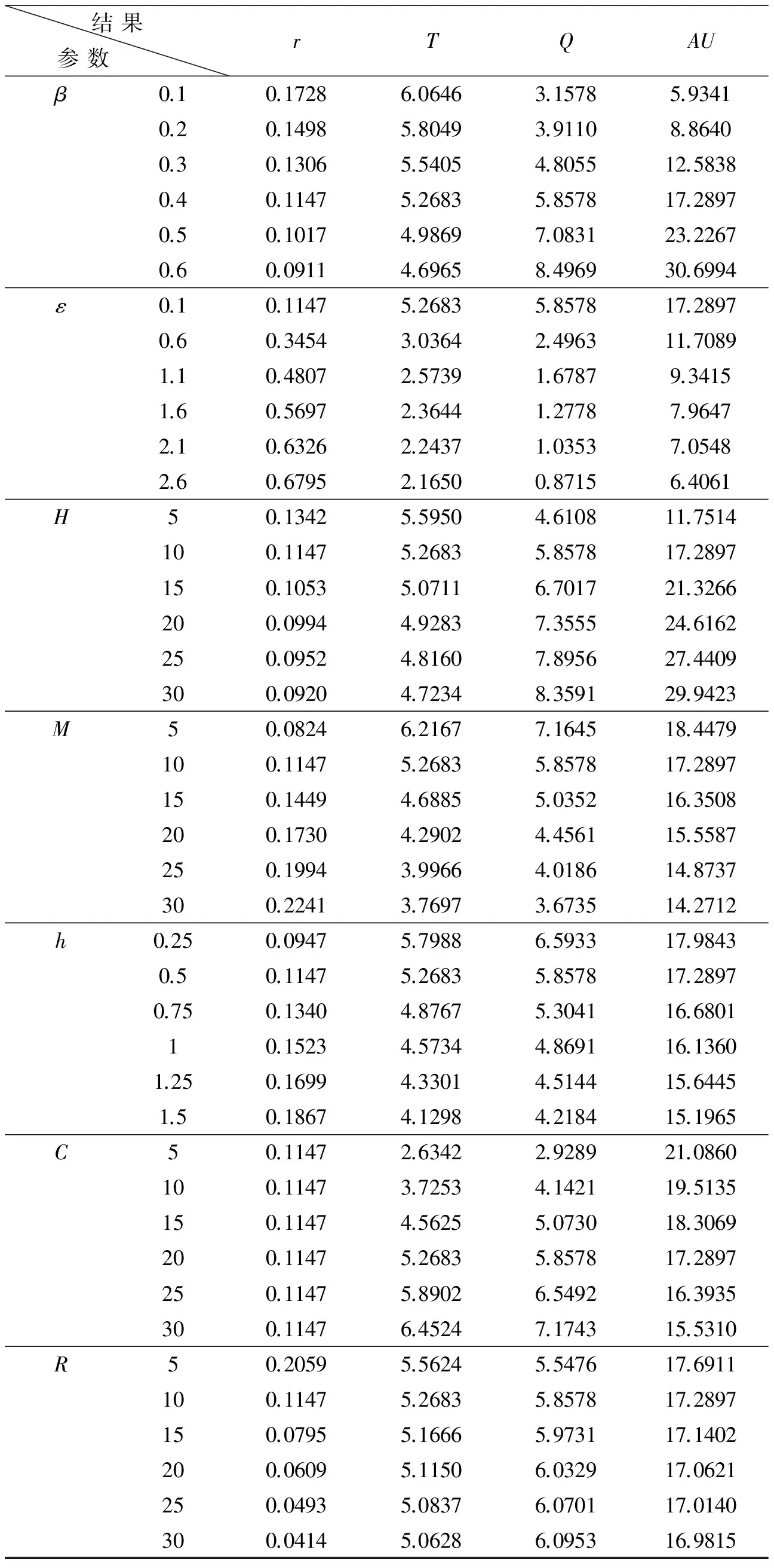
根据假设,当0≤S(t) (10) 当t′ (11) 一个周期内的销售收入为: (12) 总利润为: (13) 平均利润为: (14) 2. 当Q≤H时的库存控制模型 与上节的不同,本节考虑的是一次采购量没有达到存货临界点的情况,库存状态为: (15) 由边界条件S(t)=0,可得: (16) 当t=0时,有: 将t″=(1-r)T代入上式,得到一次订货批量为: (17) 库存持有成本: (18) 变质成本: (19) 缺货成本: (20) 总成本=订购成本+持有成本+变质成本+缺货成本,即: (21) 由于在该种库存状态下,存货量小于临界点,所以需求率保持不变,一个周期内的销售收入为: (22) 总利润为: (23) 平均利润为: (24) (二)最优解分析 (1)当采购量大于存货水平临界点(Q>H)时 (25) (26) 综合公式(25)和公式(26),即可求得最佳的订货周期T和缺货水平r。 (2)当采购量小于等于存货水平临界点(Q≤H)时 (27) (28) 综合公式(27)和公式(28),即可求得最佳的订货周期T和缺货水平r。 (三)求解步骤 第一步:将各参数代入公式(27)和公式(28),求出订货周期T和缺货水平r; 第二步:将T值和r值代入公式(17),求解得到一次订货批量Q,将其与H值比较,若Q>H,则继续第三步,若Q≤H,则转入第六步; 第三步:将各参数代入公式(25)和公式(26),求出订货周期T和缺货水平r; 第四步:将T值和r值代入假设条件t″=(1-r)T,求出库存降为零的时间t″;并将t″值代入公式(4),求出存货水平下降到临界点的时间t′;再将t′值代入公式(3),求解得到一次订货批量Q; 第五步:将各参数和第三步的T值代入公式(13),联立公式(13)和公式(14)求解得到平均利润AU; 第六步:Q即为一次订货批量; 第七步:将T值和r值代入方程(24),得到平均利润AU。 (一)算例分析 有一家生鲜农产品经销商销售某种生鲜农产品,已知该生鲜农产品的需求与其库存水平相关,销售期间价格可变,且生鲜农产品会发生变质。 假设各参数的值为:α=0.5,β=0.4,ε=0.1,H=10,M=10,h=0.5,C=20,R=10,P′=20,λ=0.15。应用求解步骤,利用MATLAB软件求解,得r=0.1147,T=5.2683,Q=5.8578,AU=17.2897。 假设各参数的值为:α=5,β=0.4,ε=2.5,H=15,M=10,h=0.5,C=20,R=10,P′=20,λ=0.15。应用求解步骤,利用MATLAB软件求解,得r=0.2854,T=2.2750,Q=25.0575,AU=162.9760。 假设不允许缺货,即r=0,R=0,探究缺货对库存控制策略的影响。假设各参数的值为:α=0.5,β=0.4,ε=0.1,H=10,M=10,h=0.5,C=20,P′=20,λ=0.15。应用求解步骤,利用MATLAB软件求解,得T=4.9569,Q=6.2256,AU=16.8126。 将结果进行比较可以发现,当允许缺货与不允许缺货进行时,订货周期会变长,同时订货批量减少,平均利润略有增加,说明允许适当缺货反而对增加收益是有帮助的。 (二)灵敏度分析 研究α、β、ε、H、M、h、C、R的变化对T、Q及AU的影响。以第一个算例的各个参数值作为参考,每次只改变一个参数的值,应用MATLAB软件对各参数进行灵敏度分析,得到的结果见表1。 表1 各参数灵敏度分析结果 续表1 结果参数 rTQAUβ0.10.17286.06463.15785.93410.20.14985.80493.91108.86400.30.13065.54054.805512.58380.40.11475.26835.857817.28970.50.10174.98697.083123.22670.60.09114.69658.496930.6994ε0.10.11475.26835.857817.28970.60.34543.03642.496311.70891.10.48072.57391.67879.34151.60.56972.36441.27787.96472.10.63262.24371.03537.05482.60.67952.16500.87156.4061H50.13425.59504.610811.7514100.11475.26835.857817.2897150.10535.07116.701721.3266200.09944.92837.355524.6162250.09524.81607.895627.4409300.09204.72348.359129.9423M50.08246.21677.164518.4479100.11475.26835.857817.2897150.14494.68855.035216.3508200.17304.29024.456115.5587250.19943.99664.018614.8737300.22413.76973.673514.2712h0.250.09475.79886.593317.98430.50.11475.26835.857817.28970.750.13404.87675.304116.680110.15234.57344.869116.13601.250.16994.33014.514415.64451.50.18674.12984.218415.1965C50.11472.63422.928921.0860100.11473.72534.142119.5135150.11474.56255.073018.3069200.11475.26835.857817.2897250.11475.89026.549216.3935300.11476.45247.174315.5310R50.20595.56245.547617.6911100.11475.26835.857817.2897150.07955.16665.973117.1402200.06095.11506.032917.0621250.04935.08376.070117.0140300.04145.06286.095316.9815 由表1可知: (1)对订货周期T的影响最大的参数是一次订货成本C,随着C的增加,T也增加;其次是变质率参数ε和尺度参数α,二者的变化都会使订货周期T呈现相反方向的小幅度变化;最后是单位产品购买成本M,M增加则T变短。 (2)对初始采购批量Q的影响最大的参数是尺度参数α,α的改变会引起Q一致的变化;其次是形状参数β、变质率参数ε和单位产品购买成本M,不同的是,β增加,Q增加;而ε和M增加,Q减少。 (3)对平均利润AU的影响最大的参数是尺度参数α和形状参数β,二者微小的变化也会带动AU剧烈的同方向的变化;其次是存货水平临界点H,AU与其呈现同方向变化;变质率参数ε和单位产品购买成本M对平均利润也有较大影响,当ε和M增大,AU减少,当ε和M减少,AU增大。 本文假设生鲜农产品的需求受到存货水平影响,通过改进原有EOQ模型中价格不变的假设条件,结合生鲜农产品的变质特点,以经销商一定周期内的平均利润最大化为目标,建立了随机需求条件下生鲜农产品库存控制模型,并利用算例证明模型有效性,结合灵敏度分析各参数对库存控制策略的影响。从研究结果可以得出以下库存控制策略: (1)平衡各项成本,做出最优决策。上述分析结果显示,允许适当缺货反而对增加收益是有帮助的,这可以解释为,当不允许缺货时可以通过增加库存量或减少订货周期的方式来达到要求,但是这两种做法却会带来额外的库存持有成本、变质成本和订货成本。额外增加的这部分成本较之缺货成本有过之而无不及,于是导致平均利润下降。所以经销商在做决策时,不能避重就轻,要平衡购买成本、库存持有成本、变质成本、缺货成本之间的关系。这是比物流当中的“效益背反”现象更为复杂的情况,是购买成本、库存持有成本、变质成本与缺货成本之间的“较量”,要求生鲜农产品经销商理性分析,从而做出更加明智的决策。 (2)减少品质影响,增加销售收入。经过灵敏度分析,发现变质率参数ε对于目标函数平均利润有较大影响,ε增大,则平均利润减少。这是因为,在模型中假设生鲜农产品变质率与需求率呈现负相关关系,于是当变质率参数增大的时候,变质率θ(t)也增大,这意味着生鲜农产品在存储的过程中发生了更多的损耗。当生鲜农产品发生变质,所带来的影响不仅是增加了变质成本,还会影响需求,导致需求率下降。对于易腐品而言,存货水平是影响消费者需求的关键因素,而存货之所以影响需求是由于,当生鲜农产品的存货越来越少的时候,顾客会认为剩下的是被先前的消费者挑过的,新鲜度不高。所以,在一个周期内,在存货影响需求且生鲜农产品新鲜度影响需求的确定性假设下,要保持展现给消费者的库存量的充足,并及时将有受损的、新鲜度下降的“次品”挑选出来降价处理或作为“赠品”赠送给消费者,以此保证正式销售的产品的新鲜度。要做好保质保鲜工作,好的品质是赢得消费者信赖的资本,做好生鲜农产品的保鲜包括三个方面,一是抑制其呼吸作用,二是抑制病菌的生长,三是控制其本身水分蒸腾作用,具体的办法就是将其储存在低温、湿度适宜而且氧气浓度低的环境。 (3)控制购买成本,提高经营效益。开源节流是提高收益的两大关键手段,在不能有效开源的情况下,节流就成为提高收益的有效方式。随着各行各业对采购的重视,采购所带来的效益日益增强,采购已然成为获取利润的又一源泉。经过灵敏度分析,发现单位产品购买成本M对平均利润也有较大影响,单位产品购买成本M的增加会导致平均利润的降低。但是降低购买成本并不是单纯的控制价格,而是买到物有所值的产品。因此,在生鲜农产品采购过程中,要特别注意以下三点:第一,供方控制,对于供应方的选择,要做好供应商信誉度调查,以此对供应方所提供的产品的价格和质量有所把握,并可以更好地进行谈判,知己知彼,百战不殆;第二,价格控制,做到货比三家,而且要比价格、比质量、比距离,选择性价比最高的;第三,质量控制,做好质量控制是利益得失的一道闸门,具体就是指产品质量的检查,以防供应商以次充好。 本文仅考虑经销商层面上的库存控制问题,未来还可以在以下方面做进一步的研究:将生鲜农产品的库存问题扩大到供应链层面,优化整条供应链的库存控制问题;研究订货提前期不为零,以及补充率有限的情况下的生鲜农产品的库存控制问题。 注释: [1] 第25届批发市场(WUWM)代表大会暨展会新闻发布会,2007年。 [2] Baker R. C.,Urban T L., “A deterministic inventory system with an inventory-level-dependent demand rate”,JournaloftheOperationalResearchSociety,vol.39(1988),pp.823-831. [3] Datta P.,“ A note on an inventory level dependent demand rate”,JournaloftheOperationalResearchSociety,vol.41(1990),pp.971-975. [4][19] Fujiwara O. U. L.,“ EOQ models for continuously deteriorating products using linear and exponential penalty cost”,EuropeanJournalofOperationalResearch,vol.70,no.1(1993),pp.104-114. [5][18] Padmanabhana G. and Prem V.,“ EOQ models for perishable items under stock dependent selling rate ”,EuropeanJournalofOperationalResearch, vol.86,no.2(1995),pp.281-292. [6] 徐贤浩、李锐娟:《存货影响销售率的短生命周期物品库存管理》,《系统管理学报》2007年第2期。 [7] 但 斌、陈 军:《基于价值损耗的生鲜农产品供应链协调》,《中国管理科学》2008年第5期。 [8] 肖勇波、陈 剑、徐小林:《到岸价格商务模式下设计远距离运输的时鲜产品供应链协调》,《系统工程理论与实践》2008年第2期。 [9]凌六一、郭晓龙、胡中菊、梁 樑:《基于随机产出与随机需求的农产品供应链风险共担合同》,《中国管理科学》2013年第2期。 [10] 邓 琪:《基于变质损耗的生鲜农产品订货策略》,《统计与决策》2013年第6期。 [11] 王 磊:《保鲜影响消费者效用的生鲜农产品订货、定价及供应链协调》,重庆:重庆大学博士学位论文,2013年。 [12] Manish S.,Sanjay J.,“Agri-fresh produce supply chain management: a state-of-the-art literature review”,InternationalJournalofOperation&Productionmanagement,vol.33,no.2(2013),pp.114-158. [13] Fan Tijun,Chang Xiangyu,Gu Chunhua,et al.,“ Benefit of RFID technology for reducing inventory shrinkage”,InternationalJournalofProductionEconomics,vol.147,no.3(2014),pp.659-665. [14] 王丽娟、侯云先:《Weibull分布的生鲜农产品库存控制》,《武汉大学学报》(理学版)2014年第2期。 [15] 李 琳、范体军:《零售商主导下生鲜农产品供应链的定价策略对比研究》,《中国管理科学》2015年第12期。 [16] 邱洪全:《信息共享下生鲜农产品供应链库存的建模与仿真研究》,《物流技术》2016年第4期。 [17] Gupta R.,Vrat P.,“Inventory model for stock-dependent consumption rate”,Opsearch,vol.23,no.1(1986). [责任编辑:黄艳林] 2016-09-06 福州大学科研启动基金项目(XRC201502) 王金妹, 女, 福建莆田人, 福州大学经济与管理学院副教授, 博士。 陈小琼, 女, 福建泉州人, 福州大学经济与管理学院硕士研究生。 C93-03 A 1002-3321(2016)06-0020-09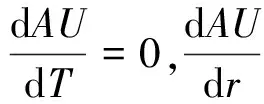
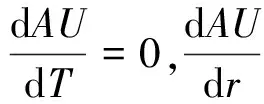
三、算例及灵敏度分析
四、结论
