耦合神经网络的同步

苏秀婷

(浙江师范大学 数理与信息工程学院，浙江 金华321004)

耦合神经网络的同步

苏秀婷

(浙江师范大学 数理与信息工程学院，浙江 金华321004)

从通道噪声、突触类型等方面对由兴奋性和抑制性神经元所组成的神经网络的同步性进行研究，结果表明：通道噪声变小,神经网络的同步性会逐渐增强；兴奋性突触有助于促进神经网络的同步，而抑制性突触会抑制网络的同步；但随着膜面积的增加，抑制性突触对神经网络的同步影响逐渐变小.

神经元；通道噪声；膜面积；突触

随着科学的发展，人们对神经元模型的研究和对大脑的认识越来越深入，然而合适的神经元模型是构造神经动力学模型的基础．1952年，Hodgkin等通过对枪乌贼巨轴突的实验，得到了4维的Hodgk-in-Huxely神经元模型(简称HH模型)[1-2]．1961年，FitzHugh提出了它的2维简化版本．1962年，Nagumo等提出了等效电路，这个简化模型即为FitzHugh-Nagumo模型(简称FN模型)．

噪声普遍存在于自然界的各个领域，在神经元非线性动力学系统方面噪声已有一定的研究．噪声分为外噪声(如突触噪声)和内噪声(如通道噪声)，当神经细胞大小有限时，离子通道噪声的随机动力学会导致膜电位的阈下波动，并且影响神经元的动力学性质[3-7]．

近年来，非线性随机系统的同步现象已吸引了各专家学者的广泛关注．而在神经系统中，神经元的同步活动在大脑的信息处理过程中扮演了重要的角色[8]．目前在神经系统中发现了很多同步现象，如化学突触在ring神经网络上引发的爆发式同步现象[9]，噪声在HH神经网络[10]和小世界神经网络[11]上引发的同步现象，等．

本文以随机的HH模型为基础，构建一个具有N个神经元(其中NE(80%)个兴奋性神经元和NI(20%)个抑制性神经元)所组成的神经网络模型，研究分析了通道噪声、突触类型和耦合强度对HH神经网络同步的影响．

1 模型

神经信息传递是以神经元动作电位的发放和传递为基础，成千上万个神经元通过突触连接而形成耦合的神经系统[2]．本文考虑一个具有N个神经元(其中NE(80%)个兴奋性神经元和NI(20%)个抑制性神经元)所组成的神经网络，每个神经元膜电位遵循以下随机HH方程[1-2]

gK(Vi,t)(Vi(t)-EK)+

gNa(Vi,t)(Vi(t)-ENa)]+Iexc+Iinh；

(1)

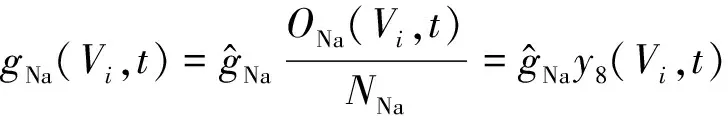
其中NK=ρK·A,NNa=ρNa·A分别表示钾、钠离子通道的总数，以上参数符号的意义及取值如下：

单位膜电容Cm=1 μF/cm2；

漏电的反转电位EL=-54.4 mV；

钠通道的反转电位ENa=50 mV；

钾通道的反转电位EK=-77 mV；

漏电导gL=0.3 ms/cm2；

膜面积A，μm；

Na离子通道密度ρNa=60 channel/μm2；

K离子通道密度ρK=18 channel/μm2；

OK(Vi,t)为t时刻处于开状态的钾通道数；

ONa(Vi,t)为t时刻处于开状态的钠通道数.

因不同离子通道所处的状态有所不同，故每个神经元的离子通道各状态间的相互转换可用Markov过程来描述,钠通道见式(2),钾通道式(3)．

(2)

(3)

其中mi 3hi 1对应的是钠通道的打开状态，ONa(Vi,t)是处于mi 3hi 1状态的钠通道数．ni 4对应的是钾通道的打开状态，OK(Vi,t)是处于ni 4状态的钾通道数．电压依赖的转换速率为：

(4)

当反应发生时，系统的状态会随之改变.每一个反应Rk,(k=1,2,…,28)都对应一个状态改变向量νk和一个定义在状态空间上的反应速率函数λk(X,V).若以xk(Vi,t)表示t时刻处于Sk(k=1,2,…,13)状态的离子通道个数，则反应速率函数λk(X,V)为相应的转换速率乘以t时刻处于状态Sk(k=1,2,…,13)的离子通道个数．令

而

则对于每个神经元YNa(Vi,t)和YK(Vi,t)满足以下Langevin方程:

(5)

(6)

其中Wk(t),k=1,2,3,…,28,为彼此独立的Wiener过程．

图1为神经网络连接方式.按图1连接方式，兴奋性突触输入Iexc和抑制性突触输入Iinh可分别表示如下[12]:

E—兴奋性神经元群体 I—抑制性神经元群体图1 神经网络连接方式

(7)

(8)

(9)

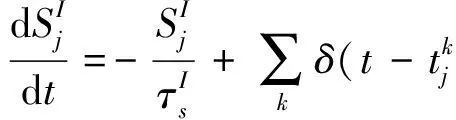
(10)

同步指数可用于衡量神经网络中神经元发放的同步程度，其定义如下:假设把一个较长的时间段T进行m等分并且窗口大小为τ，两个神经元i和j的锋电位序列分别为Xi(l)=0或1，Xj(l)=0或1，l=1,2，…，m(T/m=τ)，其中1代表神经元发放，0代表不发放，则两个神经元之间的相干性指标为:

(11)

则神经元同步指数C就是许多对神经元之间相干性指标Cij的均值.

(12)

2 数值仿真

本文分析通道噪声、突触类型和耦合强度对上述HH神经网络同步性的影响．图2是耦合强度为g=5ms/cm2)，取不同连接概率(RE、RI)和膜面积A时神经网络的发放模式．由图2可以看出，当膜面积A不变时，随着连接概率RE的增加和RI的减少，神经元发放越来越同步；当连接概率RE和RI不变时，随着膜面积A的增大，神经元的发放越来越同步且越来越少；但当膜面积A增大到一定程度时，神经网络的同步性慢慢趋于稳定.这表明通道噪声[3-7]和突触类型会对神经网络的同步产生一定的影响．

为了衡量神经元发放的同步程度，图3给出了在不同膜面积A下，连接概率RE、RI与同步指数C的关系．由图3可见，当膜面积A不变时，同步指数C随着连接概率RE增大而增大，随着连接概率RI的增大而减小.但当膜面积A较大时，随着连接概率RI的增大，同步指数C只是轻微减小．这表明兴奋性突触有助于促进神经网络的同步，而抑制性突触会抑制网络的同步，但随着膜面积A的增加即通道噪声的减小，抑制性突触对神经网络的同步性能影响越来越小．

图2 不同的连接概率RE、RI和膜面积所对应的神经网络发放模式

图3 不同膜面积下连接概率RE和RI与同步指数C的关系

为了进一步研究通道噪声和突触类型对神经网络同步的影响，以下从不同耦合强度g下探讨神经网络的同步情况．

图4为在不同耦合强度g下膜面积A与同步指数C的关系.由图4可见，在固定耦合强度g且连接概率RE=0.5和RI=0.5时，随着膜面积A的增大同步指数C逐渐增大，而当膜面积A增大到一定程度时，同步指数C保持在一定的水平，即使耦合强度g不同，这种趋势仍然相同；这表明当膜面积A很小即通道噪声很大时，神经网络同步性很差，而随着膜面积A的增加也就是通道噪声变小时，神经网络的同步性会逐渐增强，但膜面积A增加到一定程度时，神经网络的同步程度会保持在一定的水平上.

图5为在不同耦合强度g下膜面积A与发放率的关系．由图5可见，当固定耦合强度g时，神经网络的发放率随着膜面积A的增大而减小；而当增大耦合强度g时，神经网络的发放率变化并不明显．这表明随着通道噪声的变小，神经网络发放率会逐渐减小，而耦合强度g对神经网络发放率的影响并不明显．

图6为在不同膜面积A和耦合强度g下，连接概率RE、RI与同步指数C的关系．从图6可以看出，当固定膜面积A和耦合强度g时，随着连接概率RE的增大，同步指数C逐渐增大，而随着连接概率RI的增大，同步指数C逐渐减少；即使耦合强度g不同，这种趋势仍然相同.当固定膜面积A时，随着耦合强度g的增大，同步指数C有增加的趋势，但会慢慢保持在一定的水平．这进一步表明兴奋性突触可促进神经网络的同步，而抑制性突触会抑制网络的同步；并且增加耦合强度g有利于提高神经网络的同步．

图4 膜面积与同步指数C的关系 图5 膜面积与发放率的关系

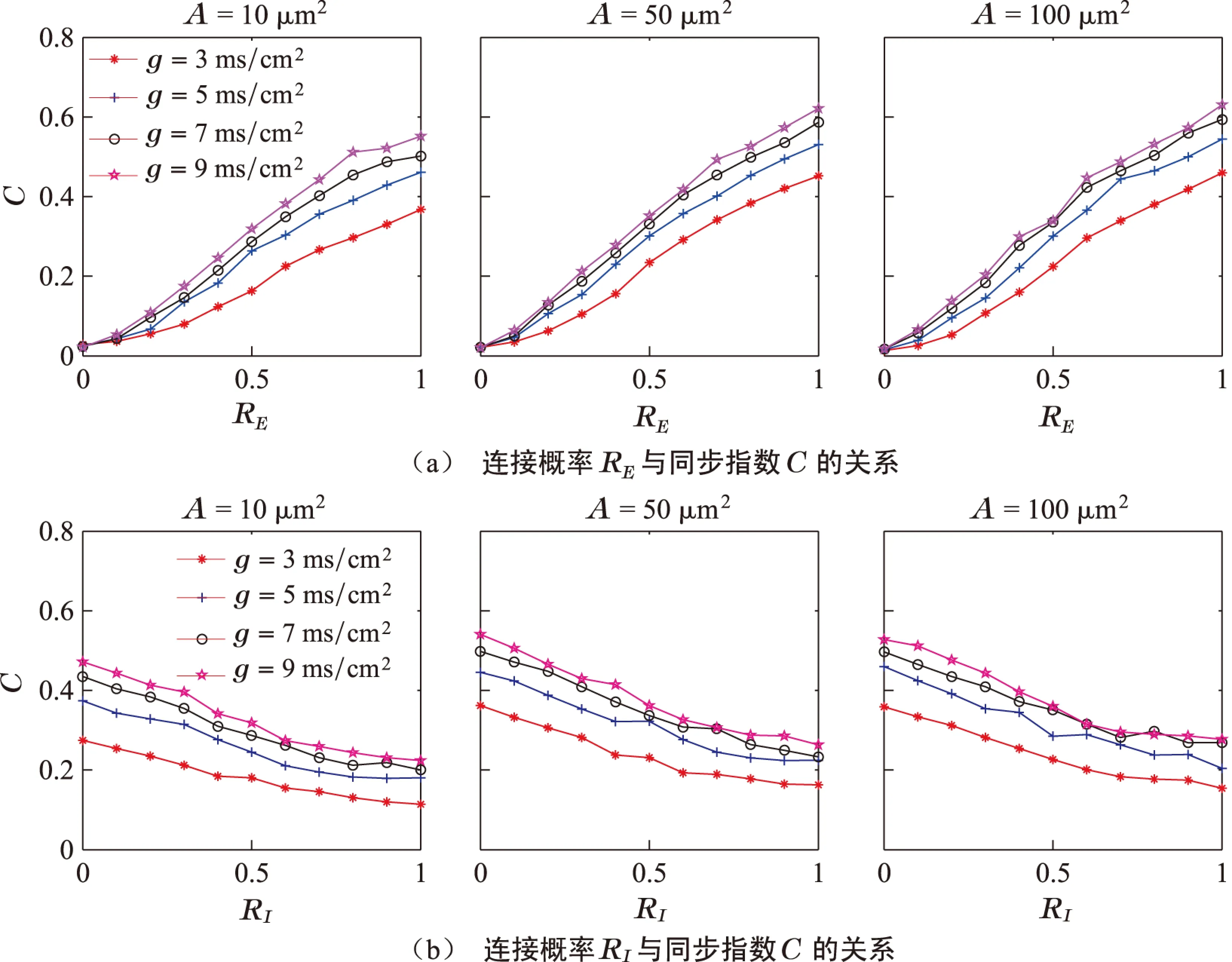
图6 不同膜面积A和耦合强度g下连接概率与同步指数的关系

3 结论

通过以上数值分析结果可知：1)当膜面积A很小即通道噪声很大时，神经网络同步性很差；而随着膜面积A逐渐变大即通道噪声变小时，神经网络的同步性会逐渐增强；但膜面积A增加到一定时，神经网络的同步程度会保持在一定的水平．2)神经网络的发放率随着膜面积A的增大而减小，而耦合强度g对神经网络的发放率影响并不明显．3)兴奋性突触有助于促进神经网络的同步，而抑制性突触会抑制网络的同步；但随着膜面积A的增加，抑制性突触对神经网络的同步性能影响越来越小．4)增加耦合强度g有利于提高神经网络的同步．

[1]王青云,石霞,陆启韶.神经元耦合系统的同步动力学[M].北京：科学出版社,2008.

[2]阮迪云.神经生物学[M].合肥：中国科学技术大学出版社,2008.

[3]CHOW C C，White J A.Spontaneous action potentials due to channel fluctuations[J].Biophysical Journal,1996，71(6)：3013-3021.

[4]STEINMETZ P N,MANWANI A,KOCH C,et al.Subthreshold voltage noise due to channel fluctuations in active neuronal membranes[J].Journal of computational neuroscience,2000,9(2):133-148.

[5]OZER M,GRAHAM L J.Impact of network activity on noise delayed spiking for a Hodgkin-Huxley model[J].The European Physical Journal B,2008,61(4):499-503.

[6]SCHMID G,GOYCHUK I,HNGGI P.Channel noise and synchronization in excitable membranes[J].Physica A:Statistical Mechanics and its Applications,2003,325(1):165-175.

[7]SCHNEIDMAN E,FREEDMAN B,SEGEV I.Ion channel stochasticity may be critical in determining the reliability and precision of spike timing[J].Neural Computation,1998,10(7):1679-1703.

[8]SINGER W.Synchronization of cortical activity and its putative role in information processing and learning.[J].Physiology,1993,55(55):349-374.

[9]WANG Q Y,Lu Q S,Chen G R.Ordered bursting synchronization and complex wave propagation in a ring neuronal network[J].Physica A Statistical Mechanics & Its Applications,2007,374(2):869-878.

[10]WANG C N,MA J,JIN W Y,et al.Electric Field-induced dynamical evolution of spiral wave in the regular networks of Hodgkin-Huxley neurons[J].Applied Mathematics & Computation,2011,218(8):4467-4474.

[11]GONG Y,WANG M,HOU Z,et al.Optimal spike coherence and synchronization on complex Hodgkin-Huxley neuron networks.[J].Chem Phys Chem,2005,6(6):1042-1047.

[12]WANG X J,BUZSáKI G.Gamma oscillation by synaptic inhibition in a hippocampal interneuronal network model.[J].Journal of Neuroscience the Official Journal of the Society for Neuroscience,1996,16(20):6402-6413.

(责任编辑 邓 颖)

Synchronization of Coupled Neural Networks

Su Xiuting

(School of Mathematics, Physics and Information Engineering, Zhejiang Normal University, Jinhua, Zhejiang 321004)

Synchronization of the neural network that consists of inhibitory and excitatory neurons was studied in this paper in terms of channel noise, synapse type and other aspects. The result suggests that the lower noise is associated with the stronger synchronization of neural networks. In addition, excitatory synapses can promote the synchronization of neural networks while inhibitory synapses can destroy and inhibit it, but the influence of inhibitory synapses on neural networks gradually becomes smaller with the increase of membraneA.

neuron; channel noise; membraneA; synapse

2016-07-14

苏秀婷(1990- ),女,广东惠州人,硕士,研究方向：计算神经科学.

10.16169/j.issn.1008-293x.k.2016.09.06

O29

A

1008-293X(2016)09-0028-05